1. Introduction
The tremendous development of quantum information and probability and corresponding novel quantum technologies led to the reconsideration of quantum foundations, e.g., [
1], and, in particular, to attempts to elaborate new interpretations of quantum theory (QT): the interpretations matching the quantum information theory. Among a variety of such interpretations, we can mention the information interpretation of Zeilinger and Brukner [
2,
3,
4] (here, a quantum state represents private information about the possible results of measurement), QBism, Quantum Bayesianism, of Fuchs developed in cooperation with Mermin, Caves and Schack [
5,
6,
7] (here, a quantum state represents subjective probability about the possible results of measurement) and the operational approach to QT of D’Ariano developed in cooperation with Chiribella and Perinotti [
9,
10,
11] (derivation of QT from natural operational principles for measurements). In such interpretations of the purely information type, the physical properties of carriers and processors of information do not play any role; the quantum formalism is interpreted as a tool to predict the results of measurements. In principle, this approach is going back to Bohr and Pauli; see Plotnitsky [
12,
13]. Bohr also emphasized that QT is not about the quantum world by itself, but about the results of measurements performed on microsystems. However, Bohr’s interpretation did not have the modern subjective flavor. The present views of Zeilinger and Brukner, Fuchs, Mermin, Caves and Schack are closer to the views of Pauli, who also emphasized the role of the observer. D’Ariano, Chiribella and Perinotti are closer to Bohr. The information viewpoint on quantum states can be considered as a part of the informational physics paradigm based on Wheeler’s famous “it from bit” [
14].
This quantum information revolution, experimental, theoretical and foundational, stimulates the application of the formalism of QT, at least its information/probability part, outside physics. By neglecting the physical structure of carriers of quantum information, one opens the door to novel applications, to information transmitters and processors of any nature. Recently, the methods of QT, especially quantum information and probability, started to be widely applied in cognitive, social and political sciences, psychology, economics, finances, decision making, molecular biology and genetics; see, e.g., the monographs [
15,
16,
17,
18,
19,
20];
cf. [
21]. Such models can be called [
16] quantum-like, in contrast to real quantum physical cognitive and biological models. Quantum-like means that only the information and probability structures of QT are explored. Of course, such applications are justified only if the classical information/probability approach is inapplicable or the classical models would be too complex compared to the quantum-like models. In cognition, psychology, psychophysics and finances, one can find plenty of probabilistic data [
16,
17,
22,
23,
24,
25,
26,
27,
28,
29,
30,
31,
32,
33,
34,
35], which is difficult or may be even impossible to embed in the classical probability model (Kolmogorov, 1933 [
36]). It is natural to try to apply the quantum probability calculus (based on complex probability amplitudes and not simply on probability measures) as the most approved and established nonclassical probabilistic calculus. Its application leads to exploring the quantum information theory as generalizing the classical information theory. We also mention development on quantum-like models in molecular biology, gene expression (lactose-glucose metabolism for Escherichia coli bacteria [
37]) and in the brain’s functioning; see [
19] for a quantum-like processing of information by the brain and [
38] for a memory model based on phase matching [
39] and the optimal quantum search algorithm, Long’s algorithm [
40,
41].
In the present paper, such a quantum-like information framework is used to analyze analogs of spontaneous and stimulated emission and stimulated absorption for quanta of an information field by information agents,
i-atoms. We show that one can “clean” Einstein’s theory of spontaneous and stimulated emission and absorption [
42] from its physical elements and present the purely information model of such phenomena. We present the essentials of laser theory in the purely information approach by precessing the assumptions on the structure of state spaces of information processors.
i-atoms and information transmitters: excitations of quantized information fields. (In cognitive and social applications, one can speak about information agents.) The basic assumption is the discrete structure of state spaces related to quantization of an information analog of energy.
To find possible structures of the state space of
i-atoms composing the gain mediums, we analyze conditions leading to the coincidence of analogs of the Einstein
B-coefficients. For this purpose, we have to develop thermodynamics of quantum-like information systems. Here, we follow Schrödinger’s representation [
43] of the Gibbs approach [
44] to thermodynamics based on the exploring of ideal mental ensembles and combinatorial arguments. We formulate assumptions on information systems leading to quantum statistics (Bose–Einstein, Fermi and parastatistics). The most important assumption is simply the indistinguishability of systems. Indistinguishable systems are systems that cannot be distinguished from one another, even in principle. In quantum physics, species of identical systems include, e.g., electrons, photons and atoms.
We remark that a version of classical information thermodynamics was developed in [
45] and applied to model financial cycles, including financial crises [
46]; more generally, methods of statistical physics were widely applied to economics and finances in the framework of econophysics; see, e.g., Mantegna and Stanley [
47] and, for a quantum-like version, Haven [
48].
As in physics, in our abstract information model, the four-level laser has advantages in realization over the simplest two-level laser. Therefore, in this paper, we concentrate on the laser model based on four-level i-atoms. For such a model, we have to operate with information excitations of two different types: analogs of photons, radiation excitations, and phonons, vibration excitations. In the field picture, these are two information fields; they differ by the magnitudes of the information energy of excitations.
One of the possible applications of information laser theory is the modeling of social processes. For example, the problem of the “explanation” of recent social explosions, especially in the Middle East, but also in South Europe and the USA, has been debated actively in social and political literature. We can mention the contributions of P. Mason, F. Fukuyama, E. Schmidt and J. Cohen and I. Krastev to this debate [
49,
50,
51,
52,
53]. We point out that the diversity of opinions and conclusions is really amazing. At the moment, there is no consistent and commonly-accepted theory of these phenomena. In natural science, clarification is typically approached through mathematical modeling. We can explore this approach in social science by presenting a model of social explosions based on the quantum-like model of the information laser. However, in this paper, we want to present a very general abstract framework applicable to any kind of information agent: humans, animals, insects, cells and artificial cognitive systems. The social laser model was considered in detail in [
54], where the simplest model based on the human gain medium composed of the two-level agents was elaborated.
2. Thermodynamics from the Combinatorics of the State Distribution
In further modeling, we shall explore the thermodynamics for two types of “information gases”: (1) consisting of information transmitters, quanta of information; and (2) consisting of information processors,
i-atoms (information agents). However, this information interpretation will be used only starting with
Section 3. In the present section, we present an abstract version of thermodynamics. Although thermodynamics was created to describe the statistical behavior of physical systems, its formalism can be applied (with careful and critical rethinking) to arbitrary systems, which are characterized by the possibility of assigning them states corresponding to fixed values of some quantity, “energy”
E, which is characterized by additivity with respect to elements of an ensemble of systems.
In fact, E. Schrödinger had already performed such rethinking in his brilliant presentation of statistical thermodynamics [
43]. Thus, he did this work for us, although he did not try to apply his approach to non-physical systems. In short, Schrödinger applied the Gibbs approach based on ideal ensembles of identical systems to quantum systems and obtained quantum statistics, both the Bose–Einstein and Fermi–Dirac cases, in line with practically classical statistical considerations.
The Gibbs picture differs crucially from the physical picture due to Maxwell, Boltzmann and others. Additionally, the Gibbs picture can be practically automatically used in our mental modeling, opposite the Maxwell–Boltzmann picture. To use the latter, one has to sure that constraints imposed on physical gases can also be assumed for “information gases” (in particular, “social gases”). The validity of these constraints for nonphysical systems is not evident at all. In the Maxwell–Boltzmann picture, there are
N actually existing physical systems in actual physical interaction with each other,
i.e., gas molecules or Planck oscillators. In the Gibbs picture,
N identical systems are mental copies of the one system under consideration. What could it mean to distribute a given amount of energy between these
N mental copies? Schrödinger wrote [
43], p. 3: “The idea is, in my view, that you can, of course, imagine that you really had
N copies of your system. Fixing your attention on one of them, you find it in a peculiar kind of “heat bath” which consists of the
others.” The crucial point is that both pictures, the physical and mental ones, lead to the same results, the same theory. Moreover, the mental picture is even more easily adopted to the quantum case (the main argument from which Schrödinger’s analysis proceeded in [
43]). By operating not with an ensemble of real systems, but with a mental ensemble, we can apply the methods of statistical thermodynamics not only to physical systems, but to systems of any origin, biological, cognitive, social, political and financial. The details of the output of the Schrödinger–Gibbs derivation of the basic thermodynamical laws can be found in [
43]. We just illuminate the two basic steps of these derivations.
Step 1. (Thermodynamics of distinguishable systems) There is an ensemble (mental in general) of
N identical systems; each of them can be in one of the states
characterized by the corresponding energy levels
The state of an ensemble is determined by the indication that System No. 1 is in a state, say
, No. 2 in a state
, No.
N in a state, say
(Schrödinger is careful in his presentation, and he pointed out that one need not assume that a system has the definite value of energy as its objective property; he wrote that this value can be obtained only on “inspection”, measurement). Thus, a certain class of states of the ensemble will be indicated by saying that
of the
N systems are in the states
It is important to remark that
determine not a single state, but a class of states, precisely because the systems in the ensemble are distinguishable. The number of states belonging to this class is equal to:
with the two constraints:
where
N is the number of systems in the ensemble and
E is the total energy of this ensemble.
Now, the Gibbs method is based on the following argument. If
N is very large (ideally, infinitely large), then practically all states will belong to the class of states corresponding to the maximal value of
By taking into account the constraints (
2) and using the Lagrange multipliers
λ and
μ for these constraints, we obtain:
Form the partition function (statistical sum over states):
Then, the first multiplier can be easily found:
This is just the normalization factor. The second multiplier plays a more important role. It can be connected with average energy per a system in the ensemble:
However, in general, the functional dependence is very complex. Therefore, in thermodynamics, one assigns the direct meaning to μ as inverse to temperature, (and then, typically, the average energy is expressed as a function of temperature, The invention of temperature is based on considerations leading to the possibility to operate with a thermometer. In physics, they are justified: here, we really have various thermometers and well-established procedures to measure temperature.
However, in coming applications to information (in particular, social) “gases”, measurement of information temperature is not well established; we simply do not have good thermometers and procedures for the measurement of such a quantity. Proceeding pragmatically, we just treat the parameter μ as representing the average energy per system in the ensemble of N systems with the energy levels
By using (
3), we also obtain that the average number of systems per energy level is given by:
It is convenient to represent it in the form:
This set of equations indicates the distribution of the
N systems over their energy levels. Schrödinger remarked [
43], p. 8: “ It may be said to contain, in nutshell, the whole of thermodynamics.”
Step 2. (Thermodynamics of indistinguishable systems) Starting with the thermodynamics of distinguishable systems, Step 1, we now (following Schrödinger [
43]) present new thermodynamics of
m-particle system; particles in such a system are indistinguishable. The main aim is to find a new sum over states (partition) function
Denote by
the energy levels of a single particle. Then, a definite level (not a class of levels;
cf. Step 1 )
of the
m-particle system is indicated by the numbers
of particles on the corresponding levels and:
Hence, the partition function is:
where
means: over all admissible sets of numbers
As always, from
, we can deduce thermodynamics; in particular, we find the average value of
:
In physics, the following two cases are considered: (a) the values admitted for every
may be
(Bose–Einstein statistics); (b)
(Fermi–Dirac statistics). We remark that in physics, so-called para-statistics were also considered (at least in theoretical studies),
i.e., Case (b) may be generalized to (b)’
, where
q determines the maximal possible number of particles on the energy level
For our further applications outside physics, it is important to remark that in the Gibbs–Schrödinger derivation of quantum thermodynamics, one comes to an understanding of the necessity of the statistics of the quantum type practically automatically: there are just these logical choices for
for ensembles of compound indistinguishable systems. In principle, in further information applications, there are no reasons to restrict possible quantum(-like) statistics to (a) and (b); para-statistics of the (b)’-type are also possible. However, for a moment, we restrict our considerations to Bose–Einstein and Fermi–Dirac statistics. It is easy to see [
43] that the corresponding partition functions can be expressed as:
This leads to the following basic expression for the average value of
:
where
is the so-called parameter of degeneration,
Then, one gets the average energy as:
This is all that we need for our further thermodynamical considerations. We repeat that our outline of Schrödinger’s presentation was practically free from physics. It can be applied to any kind of systems to which we can assign a quantity analogue of the energy; its only feature is that it can be additively redistributed over subsystems. We also used the indistinguishability of subsystems, “particles”, of a compound
m-particle system. This assumption implies the specific form of the basic thermodynamical quantity: the partition function (
9). Then, we restricted considerations to standard quantum statistics, but we may proceed with any para-statistics, as well. Thus, in short, the only important feature is indistinguishability. Additionally, this is evidently not a feature of solely quantum systems.
3. Information Fields and Atoms
In our modeling, the notion of information is a primary notion, which is not definable with the aid of more fundamental notions, such as probability. Such an approach matches various purely-informational approaches to physics celebrated in Wheeler’s statement: “It from bit. Otherwise put, every ‘it’, every particle, every field of force, even the space-time continuum itself derives its function, its meaning, its very existence entirely - even if in some contexts indirectly from the apparatus-elicited answers to yes-or-no questions, binary choices, bits. ‘It from bit’ symbolizes the idea that every item of the physical world has at bottom—a very deep bottom, in most instances—an immaterial source and explanation; that which we call reality arises in the last analysis from the posing of yes no questions and the registering of equipment-evoked responses; in short, that all things physical are information-theoretic in origin and that this is a participatory universe.” We also cite Chalmers [
55] comment on this statement: “Wheeler (1990) has suggested that information is fundamental to the physics of the universe. According to this ‘it from bit’ doctrine, the laws of physics can be cast in terms of information, postulating different states that give rise to different effects without actually saying what those states are. It is only their position in an information space that counts.” We are mainly interested in the quantum theoretical version of informational physics, as the Zeilinger–Brukner informational interpretation of QT. We also mention the information viewpoint on Bohmian mechanics based on the active information interpretation of the quantum potential. This interpretation was elaborated by Bohm and Hiley [
56]. It is amazing that even an ontological model of quantum phenomena, Bohmian mechanics, naturally generates the purely information interpretation of its basic entity, the quantum potential. The active information interpretation opened the door for applications of the formalism of Bohmian mechanics outside physics, in particular in mathematical modeling of quantum-like cognition [
56,
57,
58,
59]; later, this formalism was explored in behavioral finances [
60,
61]. However, in this paper, we shall not use the Bohmian approach to quantum mechanics.
We complete the informational physics doctrine by the informational cognition doctrine, that cognition with all its derivatives, unconsciousness and consciousness (individual and social), also has the purely informational structure. Thus, we try to resolve Descartes’ body-mind dualism by assigning information the fundamental unifying feature. However, in this paper, we do not raise deep problems related to informational physics and cognition. We proceed with the following formal model.
There are two types of information systems to which the previous abstract thermodynamical considerations can be applied. The first type of systems are information processors. They can absorb and emit information. The second type of systems are information transmitters. They transmit information to and from information processors. In applications to cognitive, social and political sciences, economics and finances, information processors can be treated as information agents. However, we do not restrict the applicability of our approach to humans. For example, cells and even proteins also can be considered as information processors [
20].
The basic quantity under consideration is an information energy, which, as in the above thermodynamical considerations, has the property of additivity with respect to elements of an ensemble of systems. It characterizes the ability of information with respect to actions. In informational physics, the interrelation of information and energy (physical) plays a crucial role; see, e.g., Szilard [
62]. However, we want to proceed more generally. We do not connect the informational energy directly to the physical energy. Our formalism is applicable to other (less formalized) types of energy: mental, social or financial energy. They characterize the ability of information agents to perform mental, social and financial actions; see [
16,
19,
45,
46,
48] on the application of financial (information) energy. Thus, in the model under development, information is not simply a string of bits, zeros and ones, but it is also characterized by its potential to perform “work”, where the latter is understood as actions in information spaces;
cf. [
59].
The crucial point of our consideration is the assumption on the discrete structure of informational energy for (some) information processors. We mimic QT by assuming that they can be only in the states corresponding to the discrete levels of energy,
(for simplicity, we ignore the possibility of the degeneration of the energy levels). We also assume that they can emit only discrete portions of information energy, Bohr’s rule:
(the analog of Bohr’s quantization rule). Such information processors we call information atoms,
i-atoms.
Quanta of energy emitted by i-atoms form a kind of gas (consisting of information transmitters) or an information field. If we start with the field picture, then quanta are considered as excitations of this field (similarly to the physical quantum field theory).
It is useful to invent a variety of information fields; e.g., a field of social information; its quanta represent the ability of humans to perform social actions; or a field of private information, the quanta of which represent the ability to perform private actions. Quantum information fields of humans differ from the fields of animals, or insects, or cells. We assume that quanta of information fields satisfy the Bose–Einstein statistics. This is a very natural assumption, since various information excitations can have the same energy, the same ability to generate actions.
We understand that our approach is far from being completely formalized. This makes quantitative modeling difficult. However, it can serve as a good base for the qualitative analysis of a very general class of information phenomena. Such a qualitative analysis is very important, especially in applications outside physics, in cognition, psychology, sociology, economics and politics, where in general, the degree of formalization is not so high as in physics.
Our basic assumption is that i-atoms and fields and interaction between them can be operationally described by the mathematical formalism of QT. Formally, this assumption implies all quantum-like features of our model, including the quantum structure of energy levels and Bohr’s rule; see also spontaneous and stimulated emissions and absorption. However, the situation is more complicated. In our purely information model, we do not have physical space-time and cannot apply Schrödinger’s quantization to write the corresponding Schrödinger equation. For example, discrete energy levels for an atom are a consequence of the use of the Coulomb potential. There are no reasons to assume this potential for i-atoms precisely. Therefore, the discreteness of the energy levels of i-atoms has to be postulated. In fact, only by trying to apply the quantum formalism outside physics is it possible to understand the crucial role of Schrödinger’s quantization and the existence of the classical (Newtonian) physical model in physical space-time completely. We do not have these kinds of classical information models in cognitive and social sciences, that is models that we would be able to quantize and, as a result, be able to explore the appropriate potentials resulting from this quantization.
4. Spontaneous and Stimulated Emission and Stimulated Absorption
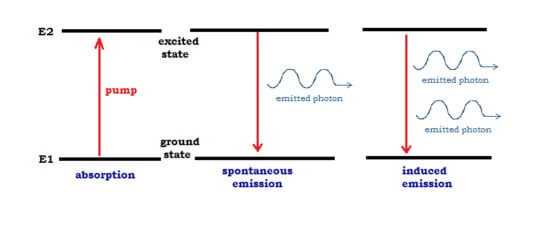
Physical processes of spontaneous and stimulated (induced) emission and stimulated absorption are illustrated by
Figure 1. We now turn to the purely informational model.
We postulate the ability of
i-atoms to spontaneously emit the quanta of information fields, in accordance with Bohr’s rule (
14). This feature is experimentally justified for information agents, at least human beings. (Humans can “emit information quanta”, e.g., in the form of communications, spontaneously and seemingly acausally. Of course, this is a complex problem of cognition closely related to the problem of free will. Additionally, we have no possibility to discuss it here at a deeper level.) However, this may be, as well, for simpler bio-systems, down to the cell level. In physics, spontaneous emission can be derived in the quantum field framework.
Figure 1.
Physics: emission and absorption of light quanta.
Figure 1.
Physics: emission and absorption of light quanta.
It is also postulated that an
i-atom imposed on an information field can absorb its excitations and emit them, again in agreement with (
14). This statement also matches the behavior of information agents. An individual imposed on a flow of information communications (which are treated as quanta of information energy) can raise her/his information energy, e.g., the social energy, potentiality to perform social actions. The presence of an external information flow can also stimulate the emission of information excitations. It is natural to assume that such processes are probabilistic, and they are characterized by coefficients of transition probabilities. The standard mathematical description is based on master equations. It is important to remark that these are classical master equations, equations for probabilities and not quantum states (density operators). In fact, we proceed with a very restricted set of quantum-like assumptions:
Now, we write the standard master equations for spontaneous and stimulated processes of exchange of the information energy. Consider two arbitrary levels of energy of the i-atom, , and the transition energy
We start with processes stimulated by an information field. In some sense, these processes are easier from the interpretation viewpoint. Then, transitions between these levels as the result of interaction with the field are described as follows. In an ensemble of
i-atoms, if the numbers of
i-atoms in these states are given by
, the rate at which stimulated emission occurs is given by:
where
is the transition probability coefficient and
is the energy density of the information field. The rate of emission is thus proportional to the number of
i-atoms (e.g., information agents) in the excited state
and to the density of incident information quanta, excitations of the information field. In physics (for the electromagnetic field), the proportionality constant
is known as the Einstein
B-coefficient for that particular transition, and
is the radiation density of the incident field at the transition energy
At the same time, there will be a process of absorption that removes energy from the field while raising the energy levels of
i-atoms, from the lower state to the upper state. Its rate is given by an essentially identical equation:
The rate of absorption is thus proportional to the number of
i-atoms in the lower state
and to the density of the information field.
The assumption of the proportionality of the right-hand sides of the equations to the numbers of systems in the corresponding states is standard for any master equation. Hence, here, the crucial point is proportionality to the field density, which is also natural. However, in principle, especially in applications outside physics, this assumption might be violated. Even in physics, this assumption has the restricted domain of validity. If a field interacts with itself, then the nonlinear character of dependence has to be taken into account. This may happen for fields of high intensity or with photons of high energy (when processes as pair production enter). Thus, by analyzing the behavior of (i-atoms) atoms in high energy (information) fields, one has to be cautious; modifications of Einstein’s theory may be needed.
Einstein showed that, for the electromagnetic field, the coefficients of transition must be equal,
i.e.,
In general, there are no reasons to expect that this equality will hold true in the general quantum-like informational model; we shall come back to this problem in
Section 5, in its last block.
Now, we turn to spontaneous emission. Here,
decays as:
where
is the rate of spontaneous emission. In physics (for the electromagnetic field), this constant is referred to as the Einstein
A-coefficient.
By taking into account both spontaneous and stimulated emission and absorption, we obtain Einstein’s balance equations:
For the state of equilibrium, we have:
Finally, we make the following important remark. In this section, we followed Einstein’s original line of reasoning [
42],
i.e., the master Equations (
19) and (
21) are valid for any pair of systems, “atoms” and “field”, which satisfy the system of Constraints 1–5. In fact, one need not require the applicability of the modern quantum theory based on the Hilbert space formalism. Thus, although following the modern line of thought, we invented information fields as quantum fields and
i-atoms as quantum systems with discrete energy spectra, in principle, we might proceed in the “old fashioned way”, as Einstein did, by using thermodynamical arguments and a number of natural constraints on the energy levels of systems. In modern quantum physics, such an approach is not so valuable, since the applicability of the quantum Hilbert space formalism is well tested and therefore commonly accepted. However, in information theory, especially its applications to sociology, politics, economics and finances, one cannot take the applicability of the standard Hilbert space formalism as granted. Here, it is more natural to start, as we did in this section, to proceed in the original Einstein manner. We shall continue in the same way in the next section.
5. Einstein Coefficients, Balance Equation
In this abstract framework, we shall not fix the concrete value of the degeneration parameter
ξ for photons; see (
12), namely
We shall neither use the concrete spacial distribution of energy, which is characteristic for photons (this leads to the concrete energy density of the photon field in the state of equilibrium of the energy exchange with atoms). We proceed with a general information boson field (gas of quanta) satisfying the thermodynamical Constraint (
12) and Assumptions 1–5 of
Section 4.
We know that for the quantum electromagnetic field interacting with atoms, Einstein’s
B-coefficients are equal. Our aim is to find how they are related in the presented abstract model of the interaction of a field of information quanta with the gas of
i-atoms with discrete levels of the information energy. In physics, the standard derivation of the equality (
17) is based on the thermodynamical arguments. One uses the balance between stimulated and spontaneous emissions in the state of equilibrium for the energy exchange between a field and the gas of atoms. In particular, the Plank law for the black body radiation plays an important role. We mimic this derivation by using not explicitly the black body radiation formula, but a more general thermodynamic formula (
12). Our final output is Formula (
30). For
, it coincides with Einstein’s equality (
17).
The density of the field energy at the state
can be found as:
As physicists often do [
43], we now proceed with the continuous energy parameter
Then:
If we write the total number of states (states of the field generating quanta) with energies between
ϵ and
as
, where
is the density of states, then the density of the energy of the field can be written as:
where
Now, we consider the gas of
i-atoms. By using Equality (
6), the classical condition of the thermodynamical equilibrium for gases of distinguishable systems (see Step 1 in
Section 2), we obtain:
Set
The balance equation for the energy exchange between “atoms” and the field has the form (see (
21)):
or:
Since this equation holds for any value of the temperature parameter
μ, (in our purely informational approach, this parameter simply characterizes the average energy; so we can say, as well, “for any value of the average energy”), we obtain the system of two equations:
In quantum physics for the electromagnetic field,
i.e., the gas of photons, the parameter
Thus, the Einstein equality (
17) holds. This prevents approaching the population inversion for gain medias consisting of two-level atoms. However, in general, for an “information gas”, there is no reasons to assume that Einstein’s
B-coefficients are equal. We have to consider two cases:
and:
The first case is similar to quantum electrodynamics; here, the population inversion for the gain media of the two levels atoms is impossible. The second case differs drastically from quantum electrodynamics: here, the population inversion is possible even for two-level atoms.
6. Amplified Stimulated Emission of Information Energy: Two-Level Model
Now, everything is prepared for the introduction of “information lasers”. Such a “laser” is based on a population of
i-atoms (information agents) with the discrete structure of the levels of the information energy for its members, gain medium. We first proceed with the simplest model: a population whose members have two levels of the information energy. Typically, the majority of
i-atoms (e.g., people) are in the ground state, the state of the minimal information (social) energy
However, by pumping the information energy into a population, its inversion can be approached: the majority of
i-atoms (people) will be in the exited state with the energy
Population inversion generated by “simple energy pumping” (
cf.
Section 7) can be approached only if the Einstein relation (
17) or, more generally, (
31), is violated,
i.e., (
32) holds. As was pointed out in the previous section, this is impossible in quantum electrodynamics, but a priori, there are no constraints preventing the realization of such an unphysical situation for general information (and in particular, social) systems.
In physics, pumping typically is of the short pulse form. A strong pulse delivers a lot of energy to the gain medium, but it has to be short, otherwise it may destroy the gain medium. The information energy pumping has to have a similar structure: a short pulse of news. When population inversion is achieved, stimulated emission is started. It can be either externally or internally generated. In the first case, emission is stimulated by a flow of coherent news, having the energy given by Bohr’s rule:
In the second case, we have the information analog of spontaneous emission: in a population that was saturated by energy pumping, one spontaneously emitted information (e.g., social) excitation can generate stimulated emission.
In any event, stimulated emission starts, and it induces a cascade of coherent (information) excitations (of the exponentially increasing strength). For example, for a human population, it leads to the coherent social action of this population, e.g., in the form of a social protest. The latter can imply the realization of huge social energy.
7. Information Laser: The Four-Level Model
The two-level model of a laser is the simplest possible. In physics, its main problem is that, here, it is difficult to approach population inversion and, hence, to perform stimulated emission of high efficiency. However, as was pointed out in the discussion about Equalities (
31) and (
32), for the stimulated emission-absorption of information excitations, the situation might be better, and the two-level model of information lasers can have interesting applications.
In physics, the best solution to the problem of population inversion is based on the use of the four energy level model. For such a model, in quantum physics, a new type of emission, different from spontaneous and stimulated emissions, plays the crucial role. This is non-radiative emission. Besides photons, quanta of the electromagnetic field, atoms can emit phonons, quanta of mechanical motion.
This is a good place to make a remark about the interpretation of quanta. Phonons, quanta of spatial motion, are “virtual,” rather than real: they are formal mathematical entities that are useful in the quantum-mechanical treatment of atoms in space. Thus, one cannot imagine a phonon as a particle flying in space. This is not possible for photons either. Quantum formalism is an operational formalism, and quanta are formal entities expressing discrete exchanges of energy. This viewpoint offers support for our argument.
It is important to note that non-radiative relaxation occurs when the energy difference between the levels is very small, and this typically occurs on a much faster time scale than radiative transitions. Thus, for such levels, one can practically (but not completely) ignore spontaneous radiative emission. We are interested in mediums composed of atoms such that electrons move quickly from a high energy level to a meta-stable level via small non-radiative transitions and then make the final move down to the bottom level via a radiative transition, by emitting a photon.
For further application to information (and, in particular, social) modeling, it is valuable to note that non-radiative transitions of large magnitudes do not occur frequently, because the crystal structure generally cannot support large vibrations without destroying bonds. However, the energy of relaxations is typically not sufficient for bonds’ destruction.
Consider
i-atoms that can interact with quantized information fields of two types, say Φ-field and
ϕ-field. Atoms and fields satisfy Assumptions 1–5 of
Section 4. The fields do not interact with each other, but interact with
i-atoms; the energy exchange matches Bohr’s rule (
14). For laser functioning, it is important that excitations of the Φ-field have essentially higher energy than excitations of the
ϕ-field. In physics, excitations of the first type are photons (radiation), and excitations of the second type are phonons.
In cognitive, social and psychological models, the Φ-field can be interpreted as representing, e.g., quanta of the social energy and the ϕ-field quanta of the private energy (the first type of the information energy describes potentiality to perform social actions, e.g., social protests; the second type describes potentiality to perform private actions, e.g., tourism, outdoors activities, children, hobbies).
Our aim is to model stimulated emission of the cascade type of coherent Φ-field quanta; the
ϕ-field quanta play a subsidiary, but non-negligible role. For example, we can model social lasers, amplified stimulated emission of a coherent wave of the social energy; see
Section 8. Here, the presence of the private activity-field
ϕ plays the crucial role in preparation for population inversion, but not the formation of the coherent output.
Consider an
i-atom with four energy levels,
, such that
, where
Denote the probability of transition from the
-level to the
-level resulting from absorption of the Φ-quantum of the energy
from the pump flow of Φ-quanta by
; the probability of transition from the
-level to the
-level resulting in the emission of Φ-quantum of the energy
is denoted by
In physics, for the quantum electromagnetic field, these probabilities are equal: the equality of the Einstein
B-coefficients; see (
17). Therefore, the standard laser master equations are written for the pump transition probability
The validity of this assumption in our informational model is a complex problem. As was shown in (
30), in general,
, and we proceed in this framework, by setting:
We also consider probabilities of relaxations, transitions from upper levels to lower ones,
, different from transition
We assume that the probability of transition from the
-level to the
-level,
, is very high; the next transition probability
is very small. Thus, the
-level is meta-stable. Then, for the next pair of levels,
transition, the probability
is again very high. We introduce the time scales of the corresponding transitions,
Here,
and
are very short, and
is essentially longer. In our information model, the notion of lifetime is well defined: the average time for a transformer of information (information agent) to stay in the state of some concrete degree of excitement. For humans, the life time for different levels of mental excitement can be measured in experimental cognitive psychology and psychophysics.
The coefficients combine spontaneous emission of quanta of both information fields. In gain mediums, which can be used for lasers, the Φ-components of and are negligibly small compared to the ϕ-components; for the coefficient , the situation is opposite: transition is practically reduced to the emission of the Φ-quanta. Coming back to modeling of coherent waves of social activity, we couple and with private actions and with social actions.
We are interested in conditions leading to the steady state with population inversion. Of course, they are well known and can be found in textbooks. Our aim is to present them in the non-physicist-friendly form and without direct coupling to the quantum electromagnetic field and the virtual quantum field representing mechanical vibrations of atoms in physical space. We proceed with two abstract quantum fields Φ and
We remark that the information interpretation assigned to these fields is not important in formal considerations. It is also useful to remark that the analysis below is based on purely classical probabilistic considerations. Quantumness has been already presented in Assumptions 1–5,
Section 4. Equations similar to the one presented below can be written for any four populations using the probabilities of transition from one population to another. We have the following basic balance equation (by dividing it by the total number
N of atoms, we can write the master equation):
Set
, where
is the probability of the
ϕ-transition from the exited state. Here, its inverse
is the life time for this state. Then:
The steady state is determined by the condition
:
Here,
is the “normalized pumping rate”. If
is small,
i.e., the probability
is high, then the normalized pumping rate is small, and the coefficient of proportionality between the number of excited
i-atoms
and the number of
i-atoms in the ground state is approximately proportional to this rate:
Thus, pumping with the coefficient
generates the steady-state regime, and the number of excited
i-atoms is given by (
37). Pumping with a higher probability of excitation generates more excited
i-atoms; a longer lifetime for the excited level has the same effect.
Now, we briefly describe the rate dynamics leading to population inversion. We write the balance equations for levels
and
:
or:
where
gives the time scale of transitions from the
-level to the levels with lower energy. For the steady state generated by pumping, we get:
Our aim is to have as many
i-atoms (information agents, humans) as possible, not in the
-state of the maximal excitement, but in the metastable
-state. Thus, to have a good laser, the condition:
has to be fulfilled. Finally,
For the steady state, we obtain:
To approach the population inversion for the pair of levels and , the coefficient β should be strictly less than one.
In lasers with good gain medium, the probability of
ϕ-field transition from the excited level with the energy
to the level with the energy
approximately equals zero, so
In such a case:
Thus, the condition of population inversion has a very simple form:
We repeat once again that no quantum physics has been involved; these are simple balance equations, which are valid for arbitrary populations; the scenarios of the exchange by the fields’ quanta is determined by the lifetimes of the levels.
8. Quantum-Like Model of the Social Laser
Our formalism can be applied to a variety of information phenomena; in light of my previous studies [
16,
59], I am interested very much in mental models. For example, consider a population of information agents (humans). Their information (mental) energy represents potentiality for mental actions. For simplicity, we restrict considerations to social actions, by ignoring for a moment private activities. Here, we can speak about the social energy. In this framework, we formulate a theory of social lasers, amplifiers of the social energy (potentiality for social actions) by stimulated emission as the result of pumping of the social-mental energy with the aid of the information field generated by mass-media, including TV, newspapers and the Internet. The social laser would work only in populations/societies in which individuals have the discrete structure of the levels of the social energy. In the simplest case, populations in which individuals can occupy only two mental states:
the ground state (family-job-family-vocations-...); the social energy equals ;
the excited state (socially active life); the social energy equals , where
It is important that in the population/society that can serve as a kind of human gain medium, the difference has to be the same for all individuals (besides a small fraction). Such a population has to have the homogeneous structuring of social energy. Larger deviation from homogeneity with respect to the magnitude of the energy gap implies less coherence in the social laser output. Quanta of information that can be emitted by an individual in the “-population” have (at least approximately) the same social energy.
For example, in modern Western society, they carry the information about potential actions of the same energetic magnitude, say anti-globalization, “occupy Wall Street”, for/anti-abortion, gay and refugee support actions. Social actions of higher magnitude, such as the preparation of revolution, are absent (the number of individuals with such an attitude is negligible compared to the total population). The same is valid for the absorption of quanta of social energy. The majority of the population is sensitive only to information of the energy magnitude matching with the social energy structure of this society. Quanta of information carrying too high energy are ignored. For example, the message “Half of the world’s animals disappeared since 1970?” (the Living Planet Index, an assessment of vertebrate populations, shows that between 1970 and 2010, terrestrial and marine vertebrate populations both declined by 39%, and freshwater vertebrates declined by a whopping 76%; altogether, the total rate of decline for vertebrates was 52%, meaning their populations have been cut in half since 1970) is not absorbed by the standard social atom; the energy of this communication does not match the standard gap of our society.
To approach population inversion, such an energy-structured gain medium (human population) has to be exposed to a pump of information communications carrying the energy of the magnitude
After population inversion is achieved, either spontaneous or stimulated emission of an information quantum generates a cascade of coherent information quanta. The social laser produces an exponentially increasing cascade of coherent social actions, e.g., a wave of coherent social protests. The social laser can be used to model recent social protests that have spread throughout the world, from the Middle East to South and Eastern Europe and the USA. In social and political sciences, this wave of social protest is the subject of stormy debates, and plenty of mutually-contradicting explanations were presented, for example [
49,
50,
51,
52,
53]. We tried to explain the generation of such waves of coherent social actions as a natural feature of the modern information society; see [
54] for details.
Further discussion on the concepts of information, psychical (mental) and social energy will be presented in
Appendix A; in
Appendix B we shall discuss the discrete structure of energy levels of physical and social atoms in more detail.
9. Concluding Remarks
By starting from the information approach to quantum physics, Zeilinger–Brukner, Fuchs
et al., D’Ariano
et al. (and physics in general, e.g., Wheeler’s “it from bit”), we presented a model of exchange by excitations between abstract information processors (information agents) and quantized information fields. The key element of this model is the notion of the information energy, the introduction of which is supported by the thermodynamical analysis in
Section 2. The latter was performed in the Gibbs–Schrödinger framework [
43] by working with ensembles of mental copies of an information system. Here, the quantum partition function can be derived in a very abstract setting by exploring only the indistinguishability of systems. In this abstract informational setup (in the same way as in “genuine quantum physics”), one can find that the only possible statistics of gases composed of indistinguishable systems are either Bose–Einstein statistics or one of para-statistics (with Fermi–Dirac statistics as the simplest among the latter).
Then, starting with the basic assumption about the discreteness of energy levels for information processors/agents, we show that Einstein’s balance equations for the quantum electromagnetic field can be generalized to any quantized information field. The basic phenomena of quantum electrodynamics, spontaneous and stimulated emissions and absorption, can be represented in the abstract way: for a wide class of quantized information boson fields exchanging excitations with i-atoms (information processors/agents having the discrete structure of energy levels).
In light of the presented thermodynamical and quantum-like modeling, it becomes clear that the standard mechanism of laser functioning can be realized in the purely information framework as the amplification of information energy (potentiality for actions in the information space) by stimulated emission under the condition of population inversion for i-atoms.
The basic relation (
30) for the
B-coefficients implies that, in contrast to quantum physics,
a priori, there are no constraints for successful realization of the two-level model of the information laser: if Relation (
32) for the information analogs of Einstein’s
B-coefficients holds, then population inversion can be achieved. Another possibility is to violate the basic formula connecting Einstein’s
B-coefficients, (
30). This can be approached by modeling self-interacting information fields; for example, information flows of very high intensity or fields with excitations of very high energy, e.g., shock news in mass-media (unfortunately, the author has no expertize in such generalizations of Einstein’s theory or even whether they exist at all).