1. Introduction
One dimensional (1D) (quasi-1D) systems exhibit some of the most diverse and intriguing physical phenomena seen in all of condensed matter physics, such as charge (spin) density waves, quantum wires, quantum Hall bars, Josephson junction arrays, polymers and 1D Bose-Einstein condensates. The complete description of a solid is a complex many body problem. The particles are strongly correlated and cannot be understood by removing the interactions between them or by considering the effects of interactions as a perturbation. However, for some realistic low-dimensional strongly correlated systems a proper understanding has yet to be established through the examination of simplified exactly solvable models, in which the integrability has been considered to be one of the striking properties from the points of view of physics and mathematics. The 1D Hubbard model, in which the electron hopping is strongly disturbed by the on-site Coulomb interaction, has been mainly investigated with regard of Mott-transition through its exact solution [
1]. The supersymmetric
model [
2], which includes the spin fluctuations via antiferromagnetic coupling, is relevant to the description of electronic mechanisms in high-
superconductivity. The 1D Bariev (interacting XY) chain [
3,
4] is also a Hubbard-like integrable model of special interest, as it supports Cooper type hole pairs. Motivated by the inclusion of additional interactions, whether through internal impurities or external boundary fields, many works have been carried out to generalize these models for different boundary fields [
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16]. This provides a non-perturbative method to study the boundary impurity effects in one-dimensional quantum systems in condensed matter physics. Bariev model has been generalized in many ways. The Hamiltonian studied in [
17] included the onsite interaction and pair hopping processes. The Bariev chains with correlated single-particle and uncorrelated pair hopping were studied in [
18], but there is only one type of particle. Bariev
et al. [
19,
20] have considered the situations with multi-particle hopping and interchain tunneling, respectively. However, most of the investigated systems include only the nearest neighbor interactions; the question of how to find an integrable system with long range interaction is an interesting topic.
Schulz and Shastry [
21] presented a class of lattice and continuum fermion models which are exactly solvable by a pseudo-unitary transformation, leading to nontrivial and non-Fermi-liquid behavior, with an exponential dependence upon the interaction. The idea behind this approach is the finding of a basis (through a unitary transformation of the original Fock basis [
22,
23]) in which the model takes the form of the original Hubbard or XXZ model up to boundary twists which do not affect their solvability. Furthermore, the Schultz-Sharstry model was generalized by introducing an exponential interaction involving two spins with same orientation [
24].
In this paper, we generalize the Bariev model by introducing an Schultz-Sharstry-like exponential interaction which is dependent on the spin orientations of particles in the system. We note that the applied long-range spin-dependent interaction in the hopping term can be treated as a boundary phase twist. The phase change is in turn a function of number of particles and spins. When the Aharonov-Bohm effect is added to a 1D Hubbard chain with periodic boundary conditions it contributes to an extra phase shift related to the external magnetic flux [
25,
26], however our model can be applied both in the situation with external magnetic field and with internal field induced by impurities or spin fluctuations. We find the charge and spin excitations in our generalized model is a function of band filling, which is similar to the model proposed by Hirsch [
27] for studying the high-
superconductivity. The latter, however, is not integrable in 1D. By applying an unitary transformation we prove the integrability of our model. The model is solved in the framework of the coordinate Bethe ansatz [
28,
29]. All charge and spin momenta are determined by a set of Bethe equations. The energy spectrum is listed based on the classification of varying number of particles. These may be useful in the systems where the long-range interactions cannot be ignored by only taking account of the nearest neighbour interactions.
2. From Long-Range Interactions to a Twist Boundary Condition
To include long-range spin interactions, we introduce some coordinate dependent parameters, α, β and κ into the Hamiltonian of the standard Bariev model. The Hamiltonian of the generalized Bariev model to be studied is in the form
with
(
) being the creation (annihilation) operator of a particle with spin σ (σ being either ↑ or ↓) located at the
site,
being the number operator, and
being a step function,
i.e., θ(x) = 1 if x > 0 and θ(x) = 0 if x < 0. The anti-commutation relation is satisfied by
η is a coupling constant that influences the hopping amplitude of particles. Positive and negative values of η correspond to attractive and repulsive inter-particle interactions, respectively. It is clear that the system is reduced to standard Bariev model and is integrable if and κ all vanish. The exponential term of and is a generalized Jordan-Wigner transformation which includes interactions between the particle on the site and the occupation state of all sites on the spin chain. This can be seen clearly if we make an expansion around small α and β. If we set and take the summation of l from 1 to , the generalized Jordan-Wigner transformation will degenerate into Jordan-Wigner transformation.
For arbitrary values of α, β and κ the system described by Equation (
1) is not integrable by direct coordinate Bethe ansatz because all particles in the system are coupled through the long-range interaction. So the question now turns into how to determine these free parameters but keep the integrability. For this purpose, we introduce a special unitary transformation
where
is the spin interaction strength between two sites and
is a parameter related to the local chemical potential and magnetic field. They are all free parameters to be confirmed by specific physical models. The subscripts
l and
m are coordinate indices, and the superscripts μ,
ν are spin indices.This is similar to choosing a different basis for the coordinate Bethe ansatz calculations. We will show later that α, β and κ can be expressed in the form of ξ and ζ. Under the transformation
, the hopping term in Hamiltonian Equation (
1) turns into
while the particle number operator keeps unchanged.
For normal periodic boundary conditions, there will be a phase change of
when one particle hops from site
L to
(
in Hamiltonian Equation (
1)), where
and
p is an integer. We will give up the original boundary condition of the standard Bariev model but apply new boundary conditions which can keep the integrability of model Equation (
1). For the transformation Equation (
3), the phase shift across the boundary is determined by the relations
,
and
. Without loss of generality, we can set the phase change across the boundary to be
If we set
we can see easily that the Hamiltonian Equation (
1) can reduce to the original Bariev model by the unitary transformation
, up to a set of boundary conditions, and is integrable if
and κ all vanish. Through Equations (5)–(10), we obtain
Then for the given boundary phase shift
,
and Φ the specific expressions for α, β and κ are obtained by Equations (8)–(10) with the constraints
The total boundary twist is given by
where
is number of particles with spin σ. We note that the coefficient of the last term in Equation (
17) is
because the terms for
and
in constraint Equation (
9) do not exist.This boundary condition we will call a twist boundary condition. When
,
and Φ all take a value
, the twist boundary condition reduces to the trivial periodic boundary condition. For any chosen twist boundary condition other than the normal periodic boundary condition, if one can find parameters α, β and κ satisfying the constraints Equations (8)–(10) and (14)–(16), the Hamiltonian Equation (
1) is then solvable. The transform of Hamiltonian Equation (
1) under
U is
with the boundary term
Generally, the sites of the chain are chosen with a homogeneous distribution. So it is natural to think the effect of this boundary phase term
as an average phase shift
when a particle hops from one site to its neighbour sites. The corresponding Hamiltonian is then
where
and the basic commutation relations are kept unchanged. δ is a function of σ,
N and
, which is different from the case of a periodic chain. By comparing this with the standard Bariev model (
in Equation (
1)), one can see clearly that the introduced long-range spin interactions are equivalent to applying a twist boundary condition. However, we note that the phase shift between the neighbour sites may as well be distributed in any other way such that the sum equals
without changing any results.
3. Bethe Equations and Energy Spectrum
In the standard Bethe ansatz approach, modified for the twist boundary condition, any eigenfunction of the Hamiltonian takes a form similar to tensor products of plane waves [
30]. We consider the eigenstate corresponding to
N particles
in which the number of spin-down particles is
. In the region
, the function
f can be written as [
31]
By solving the Schrödinger equation
, the energy eigenvalue of the Hamiltonian Equation (
18) is given by
We note that the form of the energy eigenvalue does not change from the standard Bariev chain. However, we will see later that the momentum
is now spin dependent. Two-particle scattering matrices are given by
which are similar to the
matrices of the standard 6-vertex models. The two are related via a simple gauge transformation as [
32]
for
.
In general, we have
It is easy to show
which will satisfy the Yang-Baxter equation. So the integrability of the present model is kept. One can also solve the problem by constructing the R-matrix of this model following the the techniques in [
33].
The charge momentum
and spin momentum
satisfy the Bethe equations
The structure of roots for these equations depends strongly on the hopping amplitude η. The interactions between particles are repulsive when
, all particles with different spins cannot form a pair. In this situation all
must be real, which can be proved under the thermodynamical limit.
corresponds to attractive interactions in the system. Particles with different spins tend to exist in the form of cooper-pairs. The solution
corresponds to these bound states for charge excitations. If we choose two sets of quantum numbers
and
and set
, Equations (
29) and (30) then take the form
where
and
are both common integers. The quantum numbers
and
depend upon the charge and spin property in the system. From Equations (
31) and (
32) we can see that
and
are either integer or half-integer, according to the number of total particles and the number of spin-up (spin-down) particles. There are four cases,
and are both integers if N and are both odd;
and are both half-integers if N is odd and is even;
is a half-integer and is an integer if N is even and is odd;
is an integer and is a half-integer if N and are both even.
By taking the summation of Equations (
31) and (
32) over the coordinate and spin indices respectively, the momentum of the system is given as
where
. In the above calculations we have used the relation
.
In the limiting case
(
), we get
Substituting it into Equation (
24) we obtain the energy of the system
where
and
. We will not consider the situation where
, which occurs when the chain is half filled and
D is 0. Then for arbitrary combinations of
N and
we have four different cases
where
g and
h are any integers and also quantum numbers which describe the charge and spin excitations.
If we treat
as the phase shift induced by an external field, for a given
N and
the external field can only vary within a small range
otherwise the spin inversion will occur.
4. Results for General η
Generally, for a finite η it is difficult to get exact solutions of the Bethe equations. In this section we try to discuss some properties of the system when
. The root distribution of Bethe equations turns to a continuous density distribution, σ, in this case. We define functions
In the limiting case of large
L Equations (
38) and (
39) can be expressed in the form of integrals
where
Now, we can see from Equations (
31) and (
32) that the relations
must be satisfied by roots of the Bethe equations. We are ready to obtain a set of integral equations
where
.
Through a Fourier transform we obtain
For
, we have
and
. The corresponding particle densities in Equation (
41) are
and
, which means that the numbers of two spin species are the same if there is no external field.
For a more general situation, the values of
K and
are determined by Equation (
41). When the external field vanishes, the value of
must be π. From Equations (
44) and (
45) we get
The numerical solutions of the Bethe Equations (
29) and (
30) and the corresponding eigenvalues of the Hamiltonian Equation (
18) for
and
with different occupation numbers are shown in
Table 1 and
Table 2 respectively. As mentioned before, we will only consider the cases where
. By analyzing the structure of Bethe equations, we can see that if
or
the roots of the Bethe equations do not depend on η. These numerical results coincide with those obtained from the exact diagonalization of the Hamiltonian Equation (
18) and the analytical results in the limiting case,
, obtained through Equation (
36). For the
chain, we also give the eigenvalues
E with varying
, which do not change with η, as shown in
Figure 1.
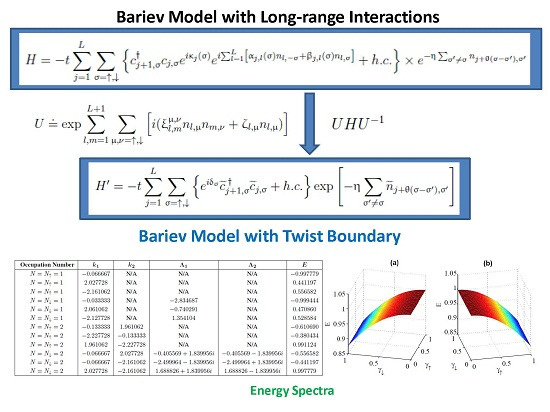
Figure 1.
The eigenvalues
E calculated from the exact diagonalization of the Hamiltonian Equation (
18) with respect to
for
. (
a)
= 1. (
b)
= 1.
Figure 1.
The eigenvalues
E calculated from the exact diagonalization of the Hamiltonian Equation (
18) with respect to
for
. (
a)
= 1. (
b)
= 1.
Table 1.
The numerical results calculated from Equations (
29) and (
30) for the parameters,
and
.
Table 1.
The numerical results calculated from Equations (29) and (30) for the parameters, and .
| Occupation Number | | | E |
|---|
| | N/A | |
| | N/A | |
| | | |
| | | |
Table 2.
The numerical results calculated from Equations (
29) and (
30) for the parameters,
and
.
Table 2.
The numerical results calculated from Equations (29) and (30) for the parameters, and .
| Occupation Number | | | | | E |
|---|
| | N/A | N/A | N/A | |
| | N/A | N/A | N/A | |
| | N/A | N/A | N/A | |
| | N/A | | N/A | |
| | N/A | | N/A | |
| | N/A | | N/A | |
| | | N/A | N/A | |
| | | N/A | N/A | |
| | | N/A | N/A | |
| | | | | |
| | | | | |
| | | | | |