Multiscale Information Decomposition: Exact Computation for Multivariate Gaussian Processes
Abstract
:1. Introduction
2. Information Transfer Decomposition in Multivariate Processes
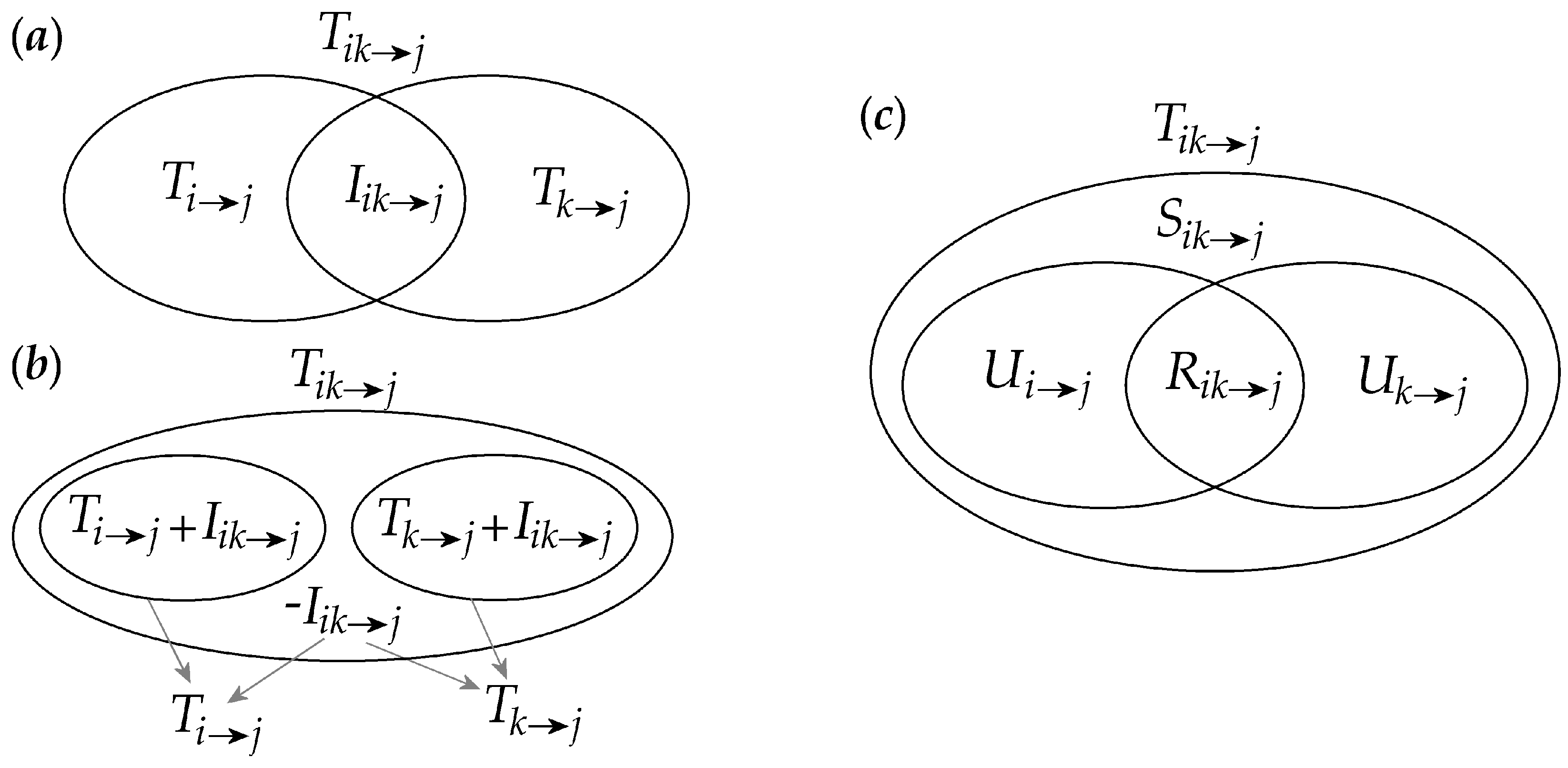
2.1. Interaction Information Decomposition
2.2. Partial Information Decomposition
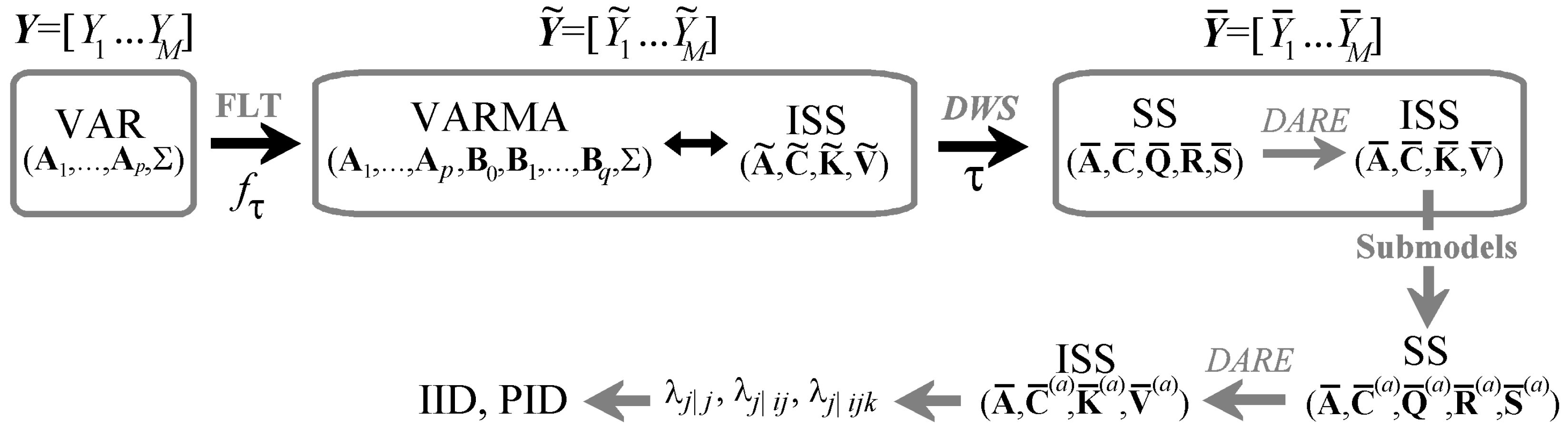
3. Multiscale Information Transfer Decomposition
3.1. Multiscale Representation of Multivariate Gaussian Processes
3.2. State Space Processes
3.2.1. Formulation of State Space Models
3.2.2. State Space Models of Filtered and Downsampled Linear Processes
3.3. Multiscale IID and PID
4. Simulation Experiment
- (a)
- isolation of and and unidirectional coupling , obtained setting ;
- (b)
- common driver effects and unidirectional coupling , obtained setting and ;
- (c)
- isolation of and unidirectional couplings and , obtained setting and ;
- (d)
- common driver effects and unidirectional couplings and , obtained setting and .
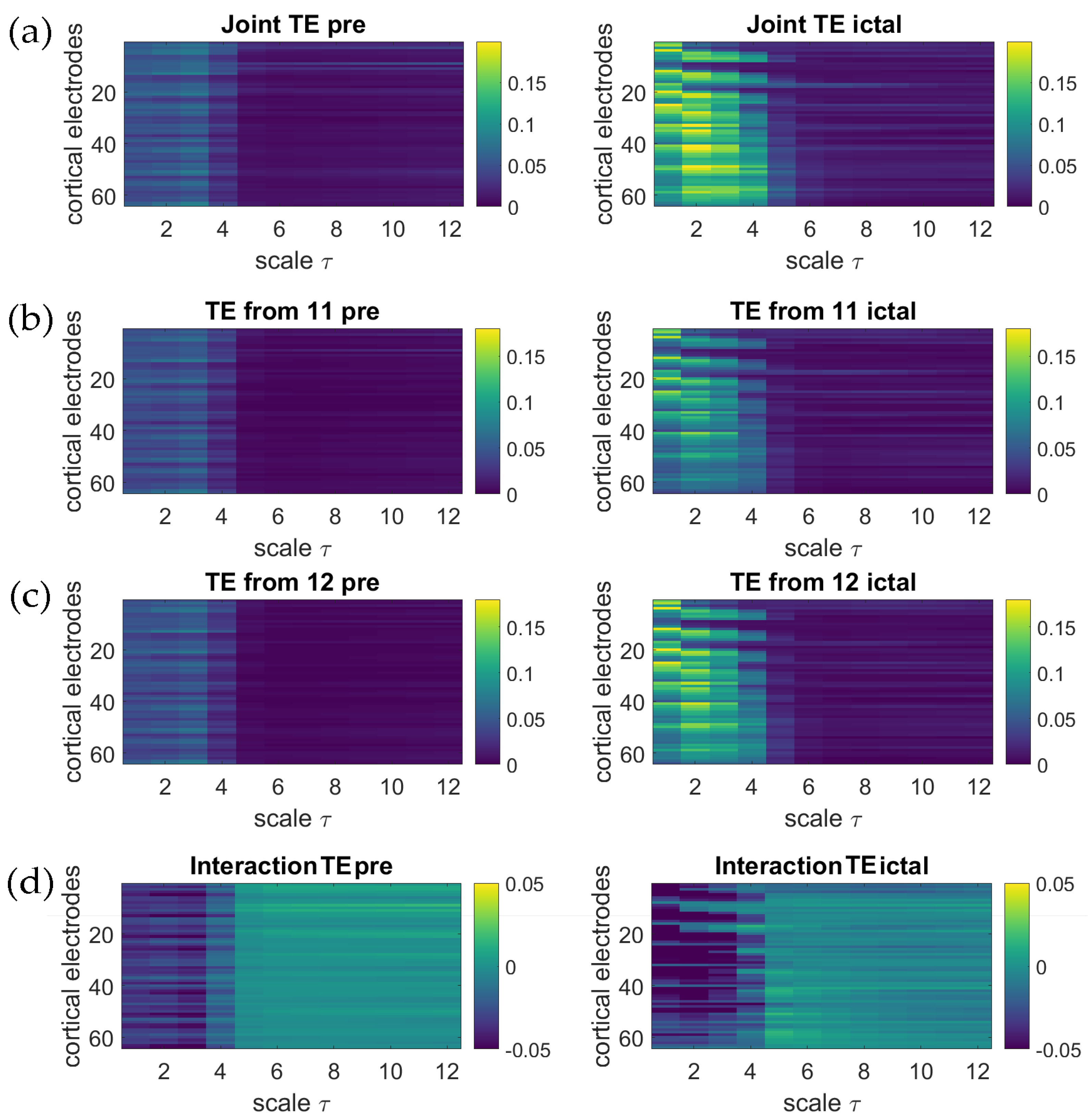
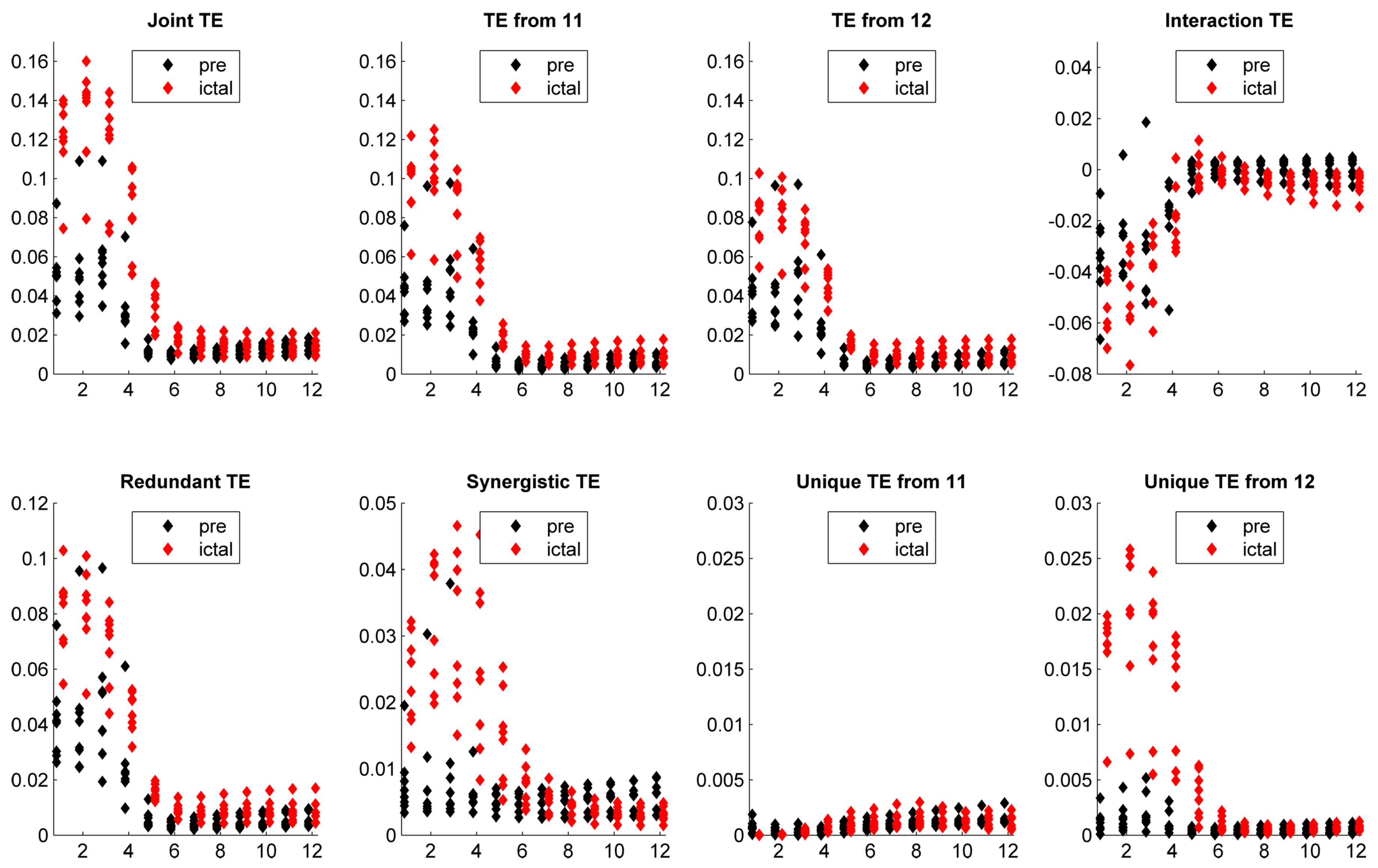
5. Application
6. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lizier, J.T.; Prokopenko, M.; Zomaya, A.Y. A framework for the local information dynamics of distributed computation in complex systems. In Guided Self-Organization: Inception; Springer: Berlin/Heidelberg, Germany, 2014; pp. 115–158. [Google Scholar]
- Pincus, S. Approximate entropy (ApEn) as a complexity measure. Chaos Interdiscip. J. Nonlinear Sci. 1995, 5, 110–117. [Google Scholar] [CrossRef] [PubMed]
- Lizier, J.T.; Prokopenko, M.; Zomaya, A.Y. Local measures of information storage in complex distributed computation. Inf. Sci. 2012, 208, 39–54. [Google Scholar] [CrossRef]
- Wibral, M.; Lizier, J.T.; Vögler, S.; Priesemann, V.; Galuske, R. Local active information storage as a tool to understand distributed neural information processing. Front. Neuroinform. 2014, 8. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, T. Measuring information transfer. Phys. Rev. Lett. 2000, 85, 461. [Google Scholar] [CrossRef] [PubMed]
- Wibral, M.; Vicente, R.; Lizier, J.T. Directed Information Measures in Neuroscience; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Lizier, J.T.; Prokopenko, M.; Zomaya, A.Y. Information modification and particle collisions in distributed computation. Chaos Interdiscip. J. Nonlinear Sci. 2010, 20, 037109. [Google Scholar] [CrossRef] [PubMed]
- Wibral, M.; Lizier, J.T.; Priesemann, V. Bits from brains for biologically inspired computing. Front. Robot. Artif. Intell. 2015, 2. [Google Scholar] [CrossRef]
- Lizier, J.T.; Pritam, S.; Prokopenko, M. Information dynamics in small-world Boolean networks. Artif. Life 2011, 17, 293–314. [Google Scholar] [CrossRef] [PubMed]
- Wibral, M.; Rahm, B.; Rieder, M.; Lindner, M.; Vicente, R.; Kaiser, J. Transfer entropy in magnetoencephalographic data: Quantifying information flow in cortical and cerebellar networks. Prog. Biophys. Mol. Biol. 2011, 105, 80–97. [Google Scholar] [CrossRef] [PubMed]
- Hlinka, J.; Hartman, D.; Vejmelka, M.; Runge, J.; Marwan, N.; Kurths, J.; Paluš, M. Reliability of inference of directed climate networks using conditional mutual information. Entropy 2013, 15, 2023–2045. [Google Scholar] [CrossRef]
- Barnett, L.; Lizier, J.T.; Harré, M.; Seth, A.K.; Bossomaier, T. Information flow in a kinetic Ising model peaks in the disordered phase. Phys. Rev. Lett. 2013, 111, 177203. [Google Scholar] [CrossRef] [PubMed]
- Marinazzo, D.; Pellicoro, M.; Wu, G.; Angelini, L.; Cortés, J.M.; Stramaglia, S. Information transfer and criticality in the ising model on the human connectome. PLoS ONE 2014, 9, e93616. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Faes, L.; Nollo, G.; Jurysta, F.; Marinazzo, D. Information dynamics of brain–heart physiological networks during sleep. New J. Phys. 2014, 16, 105005. [Google Scholar] [CrossRef]
- Faes, L.; Porta, A.; Nollo, G. Information decomposition in bivariate systems: Theory and application to cardiorespiratory dynamics. Entropy 2015, 17, 277–303. [Google Scholar] [CrossRef]
- Porta, A.; Faes, L.; Nollo, G.; Bari, V.; Marchi, A.; de Maria, B.; Takahashi, A.C.; Catai, A.M. Conditional self-entropy and conditional joint transfer entropy in heart period variability during graded postural challenge. PLoS ONE 2015, 10, e0132851. [Google Scholar] [CrossRef] [PubMed]
- Faes, L.; Porta, A.; Nollo, G.; Javorka, M. Information Decomposition in Multivariate Systems: Definitions, Implementation and Application to Cardiovascular Networks. Entropy 2017, 19, 5. [Google Scholar] [CrossRef]
- Wollstadt, P.; Sellers, K.K.; Rudelt, L.; Priesemann, V.; Hutt, A.; Fröhlich, F.; Wibral, M. Breakdown of local information processing may underlie isoflurane anesthesia effects. PLoS Comput. Biol. 2017, 13, e1005511. [Google Scholar] [CrossRef] [PubMed]
- Schneidman, E.; Bialek, W.; Berry, M.J. Synergy, redundancy, and independence in population codes. J. Neurosci. 2003, 23, 11539–11553. [Google Scholar] [PubMed]
- Stramaglia, S.; Wu, G.R.; Pellicoro, M.; Marinazzo, D. Expanding the transfer entropy to identify information circuits in complex systems. Phys. Rev. E 2012, 86, 066211. [Google Scholar] [CrossRef] [PubMed]
- Stramaglia, S.; Cortes, J.M.; Marinazzo, D. Synergy and redundancy in the Granger causal analysis of dynamical networks. New J. Phys. 2014, 16, 105003. [Google Scholar] [CrossRef]
- Stramaglia, S.; Angelini, L.; Wu, G.; Cortes, J.; Faes, L.; Marinazzo, D. Synergetic and Redundant Information Flow Detected by Unnormalized Granger Causality: Application to Resting State fMRI. IEEE Trans. Biomed. Eng. 2016, 63, 2518–2524. [Google Scholar] [CrossRef] [PubMed]
- McGill, W. Multivariate information transmission. Trans. IRE Prof. Group Inf. Theory 1954, 4, 93–111. [Google Scholar] [CrossRef]
- Bell, A.J. The co-information lattice. In Proceedings of the Fourth International Symposium on Independent Component Analysis and Blind Signal Separation (ICA), Nara, Japan, 1–4 April 2003. [Google Scholar]
- Williams, P.L.; Beer, R.D. Nonnegative decomposition of multivariate information. arXiv, 2010; arXiv:1004.2515. [Google Scholar]
- Harder, M.; Salge, C.; Polani, D. Bivariate measure of redundant information. Phys. Rev. E 2013, 87, 012130. [Google Scholar] [CrossRef] [PubMed]
- Griffith, V.; Chong, E.K.; James, R.G.; Ellison, C.J.; Crutchfield, J.P. Intersection information based on common randomness. Entropy 2014, 16, 1985–2000. [Google Scholar] [CrossRef]
- Quax, R.; Har-Shemesh, O.; Sloot, P.M.A. Quantifying Synergistic Information Using Intermediate Stochastic Variables. Entropy 2017, 19, 85. [Google Scholar] [CrossRef]
- Bertschinger, N.; Rauh, J.; Olbrich, E.; Jost, J.; Ay, N. Quantifying unique information. Entropy 2014, 16, 2161–2183. [Google Scholar] [CrossRef]
- Panzeri, S.; Senatore, R.; Montemurro, M.A.; Petersen, R.S. Correcting for the sampling bias problem in spike train information measures. J. Neurophysiol. 2007, 98, 1064–1072. [Google Scholar] [CrossRef] [PubMed]
- Faes, L.; Porta, A. Conditional entropy-based evaluation of information dynamics in physiological systems. In Directed Information Measures in Neuroscience; Springer: Berlin/Heidelberg, Germany, 2014; pp. 61–86. [Google Scholar]
- Kozachenko, L.; Leonenko, N.N. Sample estimate of the entropy of a random vector. Probl. Peredachi Inf. 1987, 23, 9–16. [Google Scholar]
- Vlachos, I.; Kugiumtzis, D. Nonuniform state-space reconstruction and coupling detection. Phys. Rev. E 2010, 82, 016207. [Google Scholar] [CrossRef] [PubMed]
- Marinazzo, D.; Pellicoro, M.; Stramaglia, S. Causal information approach to partial conditioning in multivariate data sets. Comput. Math. Methods Med. 2012, 2012, 303601. [Google Scholar] [CrossRef] [PubMed]
- Faes, L.; Kugiumtzis, D.; Nollo, G.; Jurysta, F.; Marinazzo, D. Estimating the decomposition of predictive information in multivariate systems. Phys. Rev. E 2015, 91, 032904. [Google Scholar] [CrossRef] [PubMed]
- Barrett, A.B. Exploration of synergistic and redundant information sharing in static and dynamical Gaussian systems. Phys. Rev. E 2015, 91, 052802. [Google Scholar] [CrossRef] [PubMed]
- Barrett, A.B.; Barnett, L.; Seth, A.K. Multivariate Granger causality and generalized variance. Phys. Rev. E 2010, 81, 041907. [Google Scholar] [CrossRef] [PubMed]
- Porta, A.; Bari, V.; de Maria, B.; Takahashi, A.C.; Guzzetti, S.; Colombo, R.; Catai, A.M.; Raimondi, F.; Faes, L. Quantifying Net Synergy/Redundancy of Spontaneous Variability Regulation via Predictability and Transfer Entropy Decomposition Frameworks. IEEE Trans. Biomed. Eng. 2017. [Google Scholar] [CrossRef] [PubMed]
- Ivanov, P.; Nunes Amaral, L.; Goldberger, A.; Havlin, S.; Rosenblum, M.; Struzik, Z.; Stanley, H. Multifractality in human heartbeat dynamics. Nature 1999, 399, 461–465. [Google Scholar] [CrossRef] [PubMed]
- Chou, C.M. Wavelet-based multi-scale entropy analysis of complex rainfall time series. Entropy 2011, 13, 241–253. [Google Scholar] [CrossRef]
- Wang, J.; Shang, P.; Zhao, X.; Xia, J. Multiscale entropy analysis of traffic time series. Int. J. Mod. Phys. C 2013, 24, 1350006. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef] [PubMed]
- Valencia, J.; Porta, A.; Vallverdú, M.; Clariá, F.; Baranowski, R.; Orłowska-Baranowska, E.; Caminal, P. Refined multiscale entropy: Application to 24-h holter recordings of heart period variability in healthy and aortic stenosis subjects. IEEE Trans. Biomed. Eng. 2009, 56, 2202–2213. [Google Scholar] [CrossRef] [PubMed]
- Barnett, L.; Seth, A.K. Granger causality for state-space models. Phys. Rev. E 2015, 91, 040101. [Google Scholar] [CrossRef] [PubMed]
- Solo, V. State-space analysis of Granger-Geweke causality measures with application to fMRI. Neural Comput. 2016, 28, 914–949. [Google Scholar] [CrossRef] [PubMed]
- Florin, E.; Gross, J.; Pfeifer, J.; Fink, G.R.; Timmermann, L. The effect of filtering on Granger causality based multivariate causality measures. Neuroimage 2010, 50, 577–588. [Google Scholar] [CrossRef] [PubMed]
- Barnett, L.; Seth, A.K. Detectability of Granger causality for subsampled continuous-time neurophysiological processes. J. Neurosci. Methods 2017, 275, 93–121. [Google Scholar] [CrossRef] [PubMed]
- Faes, L.; Montalto, A.; Stramaglia, S.; Nollo, G.; Marinazzo, D. Multiscale Analysis of Information Dynamics for Linear Multivariate Processes. arXiv, 2016; arXiv:1602.06155. [Google Scholar]
- Faes, L.; Nollo, G.; Stramaglia, S.; Marinazzo, D. Multiscale Granger causality. arXiv, 2017; arXiv:1703.08487. [Google Scholar]
- Aoki, M.; Havenner, A. State space modeling of multiple time series. Econom. Rev. 1991, 10, 1–59. [Google Scholar] [CrossRef]
- Oppenheim, A.V.; Schafer, R.W. Digital Signal Processing; Prentice-Hall: Englewood Cliffs, NJ, USA, 1975. [Google Scholar]
- Hannan, E.J.; Deistler, M. The Statistical Theory of Linear Systems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2012; Volume 70. [Google Scholar]
- Aoki, M. State Space Modeling of Time Series; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Earth System Research Laboratory. Available online: http://math.bu.edu/people/kolaczyk/datasets.html (accessed on 5 May 2017).
- Kramer, M.A.; Kolaczyk, E.D.; Kirsch, H.E. Emergent network topology at seizure onset in humans. Epilepsy Res. 2008, 79, 173–186. [Google Scholar] [CrossRef] [PubMed]
- Richardson, M.P. Large scale brain models of epilepsy: Dynamics meets connectomics. J. Neurol Neurosurg. Psychiatry 2012, 83, 1238–1248. [Google Scholar] [CrossRef] [PubMed]
- Dickten, H.; Porz, S.; Elger, C.E.; Lehnertz, K. Weighted and directed interactions in evolving large-scale epileptic brain networks. Sci. Rep. 2016, 6, 34824. [Google Scholar] [CrossRef] [PubMed]
- Sela, R.J.; Hurvich, C.M. Computationally efficient methods for two multivariate fractionally integrated models. J. Time Ser. Anal. 2009, 30, 631–651. [Google Scholar] [CrossRef]
- Kitagawa, G. Non-gaussian state—Space modeling of nonstationary time series. J. Am. Stat. Assoc. 1987, 82, 1032–1041. [Google Scholar] [CrossRef]
- Paluš, M. Cross-scale interactions and information transfer. Entropy 2014, 16, 5263–5289. [Google Scholar] [CrossRef]
- Papana, A.; Kugiumtzis, D.; Larsson, P. Reducing the bias of causality measures. Phys. Rev. E 2011, 83, 036207. [Google Scholar] [CrossRef] [PubMed]
- Porta, A.; de Maria, B.; Bari, V.; Marchi, A.; Faes, L. Are Nonlinear Model-Free Conditional Entropy Approaches for the Assessment of Cardiac Control Complexity Superior to the Linear Model-Based One? IEEE Trans. Biomed. Eng. 2017, 64, 1287–1296. [Google Scholar] [CrossRef] [PubMed]



© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Faes, L.; Marinazzo, D.; Stramaglia, S. Multiscale Information Decomposition: Exact Computation for Multivariate Gaussian Processes. Entropy 2017, 19, 408. https://0-doi-org.brum.beds.ac.uk/10.3390/e19080408
Faes L, Marinazzo D, Stramaglia S. Multiscale Information Decomposition: Exact Computation for Multivariate Gaussian Processes. Entropy. 2017; 19(8):408. https://0-doi-org.brum.beds.ac.uk/10.3390/e19080408
Chicago/Turabian StyleFaes, Luca, Daniele Marinazzo, and Sebastiano Stramaglia. 2017. "Multiscale Information Decomposition: Exact Computation for Multivariate Gaussian Processes" Entropy 19, no. 8: 408. https://0-doi-org.brum.beds.ac.uk/10.3390/e19080408






