A Survey of Function Analysis and Applied Dynamic Equations on Hybrid Time Scales
Abstract
:1. Basic Knowledge on Time Scales
1.1. Some Basic Knowledge of -Calculus
- (i)
- The sum are differentiable at t with
- (ii)
- For any constant is differentiable at t with
- (iii)
- The product is differentiable at t with
- (iv)
- If , then is differentiable at t with
- (v)
- If , then is differentiable at t and
1.2. Some Basic Knowledge of ∇-Calculus
2. Almost Periodic and Almost Automorphic Theory on Time Scales
2.1. Almost Periodic and Almost Automorphic Theory on Translation Time Scales
- (i)
- , where , has period .
- (ii)
- , where , has period .
- (iii)
- has an arbitrary period .
- (iv)
- , , has period .
- (i)
- for any , there is a positive number such that if the points and belong to the same interval of continuity and , then
- (ii)
- for any , there is relative dense set of ε-almost periods such that if , then for all , which satisfies the condition .
- (i)
- The points of possible discontinuity of these functions can be enumerated , admitting a finite multiplicity by the order in , so that .
- (ii)
- There exist strictly increasing sequences of numbers , , for which we have
- (H1)
- The matrix-valued function is almost periodic.
- (H2)
- is an almost periodic sequence.
- (H3)
- , where E is the identity matrix.
- (H4)
- The set of sequence is equipotentially almost periodic and .
- (i)
- Let be an equipotentially almost automorphic sequence.
- (ii)
- Let be a bounded function with respect to a sequence . We say that φ is ld-piecewise almost automorphic if, from every sequence , we can extract a subsequence such thatis well defined for each andfor each . Denote by the set of all such functions.
- (iii)
- A bounded function with respect to a sequence is said to be ld-piecewise uniformly almost automorphic if is ld-piecewise automorphic in uniformly in , where B is any bounded subset of . Denote by the set of all such functions.
- (i)
- is bounded for every bounded subset .
- (ii)
- are uniformly continuous in each bounded subset of Ω for all .
- (H1)
- The family of operators in generates an exponentially stable evolution system , i.e., there exist and such thatand for any sequence , there exists a subsequence such that
- (H2)
- , where and is uniformly continuous in each bounded subset of uniformly in ; is a weighted pseudo almost periodic sequence, is uniformly continuous in uniformly in , .
- (A1)
- The family of operators in generates an exponentially stable evolution system , i.e., there exist and such thatand, for any sequence , there exists a subsequence such that
- (A2)
- , and f satisfies the Lipschitz condition with respect to the second argument, i.e.,
- (A3)
- is a weighted pseudo almost periodic sequence, and there exists a number such thatfor all .
- (i)
- is relatively dense.
- (ii)
- If , then
- (iii)
- If , then
- (a)
- and is a well connected timescale sequence, where and k is some finite number, and are closed intervals for or ;
- (b)
- is a nonempty subsets of with for each and , where or ;
- (c)
- for all and all , we have , i.e., is an ω-periodic time scale;
- (d)
- for , for all and all , we have , where is the connected points set of the timescale sequence ;
- (e)
- if and only if is a zero-periodic time scale and if and only if ;
- (H1)
- Let A be the infinitesimal generator of a -semigroup . The moving-operator family is exponentially stable, that is, there exist , such that
- (H2)
- is local pseudo almost automorphic.
- (H3)
- There exists a nonnegative function such thatfor all and
2.2. Almost Periodic and Almost Automorphic Theory under Matched Spaces of Time Scales
- (P1)
- (Monotonicity) The function δ is strictly increasing with respect to its all arguments, i.e., ifthen implies ; if with , then .
- (P2)
- (Existence of inverse elements) The operator δ has the inverse operator and , where is the inverse element of τ.
- (P3)
- (Existence of identity element) There exists such that for any , where is the identity element in .
- (P4)
- (Bridge condition) For any and , .
- (ii)
- A continuous function is said to be δ-almost automorphic if is δ-almost automorphic in uniformly for all where B is any bounded subset of Denote by the set of all such functions.
- is uniformly continuous in any bounded subset for all
- is uniformly continuous in any bounded subset for all
3. The Uncertainty Theory on Time Scales with Shift Operators
3.1. The Stochastic Theory on Time Scales
- (i)
- If and , then
- (ii)
- If , then and the Itô-isometry holds, i.e.,
- (i)
- Let . Definition 49 can be written as:Definition 50.A subset S of is called relatively dense if there exists a positive number L such that for all .
- (ii)
- Let , Definition 49 is equivalent to the notion of relatively dense set on quantum time scale:Definition 51.A subset S of is called relatively dense if there exists a positive number such that for all .
- (iii)
- Let . The concept of relatively dense set on this irregular time scale follows immediately:Definition 52.A subset S of is called relatively dense if there exists a positive number such that for all .
- (iv)
- Let . The concept of relatively dense set in discrete situation can be stated as follows:Definition 53.A subset S of is called relatively dense if there exists a positive number such that for all .
- (i)
- there is a positive number such that if the points and belong to the same interval of continuity and , then for all ;
- (ii)
- there is relative dense set of mean-square ε-almost periods with respect to the pair such that if , then for all which satisfies the condition .
- (i)
- we say S-CCTS is with positive-direction if ;
- (ii)
- we say S-CCTS is with negative-direction if ;
- (iii)
- we say S-CCTS is with bi-direction if .
3.2. The Fuzzy Theory on Time Scales
- (i)
- for all , , ;
- (ii)
- ;
- (i)
- ;
- (ii)
- ;
- (iii)
- for ;
- (iv)
- if ;if ;
- (v)
- for or .
- (i)
- or , i.e., .
- (ii)
- Let be --Δ-differentiable at or --Δ-differentiable at , then is -Δ-differentiable at t and
- (iii)
- For any nonnegative constant , is -Δ-differentiable at t with
- (i)
- the function is -Δ-differentiable and ;
- (ii)
- the function is -Δ-differentiable and ;
- (i)
- if , , and is --Δ-differentiable, then
- (ii)
- if , , and is --Δ-differentiable, then
- (iii)
- if , , and is --Δ-differentiable, then
- (iv)
- if , , and is --Δ-differentiable, then
- (v)
- if , , and is --Δ-differentiable, then
- (vi)
- if , , and is --Δ-differentiable, then
- (vii)
- if , , and is --Δ-differentiable, then
- (viii)
- if , , and is --Δ-differentiable, then
- (i)
- A function is calledshift almost periodicfuzzy vector-valued function in uniformly for with shift operators if the ε-shift number set of fis a relatively dense set with respect to the pair for all and for each compact subset of D; that is, for any given and each compact subset of D, there exists a constant such that each interval of length contains a such thatNow, τ is called the ε-shift number of f and is called the inclusion length of .
- (ii)
- A function is called shift normal function if for any sequence of the form , where is a sequence of real numbers, one can extract a subsequence of , converging uniformly on (i.e., , , which may depend on ), such thatuniformly with respect to .
- (iii)
- Let be Δ-differentiable to its second argument. A function is called shift Δ-almost periodic fuzzy vector-valued function in uniformly for with shift operators if the ε-shift number set of fis a relatively dense set with respect to the pair for all and for each compact subset of D; that is, for any given and each compact subset of D, there exists a constant such that each interval of length contains a such thatNow, τ is called the ε-shift number of f and is called the inclusion length of .
- (iv)
- Let be Δ-differentiable to its second argument. A function is called shift Δ-normal function if for any sequence of the form , where is a sequence of real numbers, one can extract a subsequence of , converging uniformly on (i.e., , , which may depend on ), such thatuniformly with respect to .
- (i)
- is continuous on if and only if f is continuous on .
- (ii)
- is S-almost periodic if and only if f is S-almost periodic.
- (iii)
- If f is gH-Δ-differentiable on , then is Δ-differentiable on and for .
4. The Quaternion Theory on Time Scales
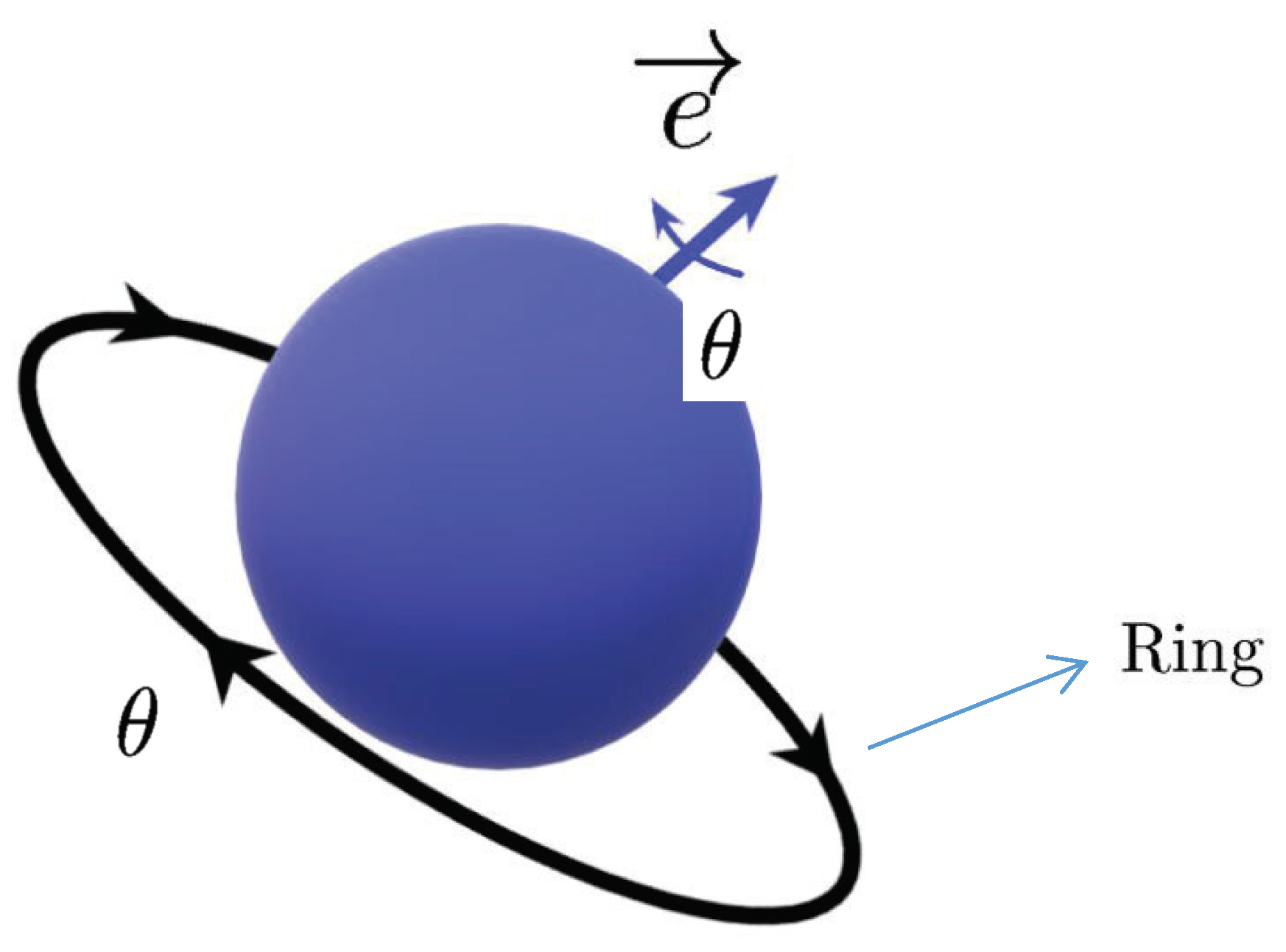
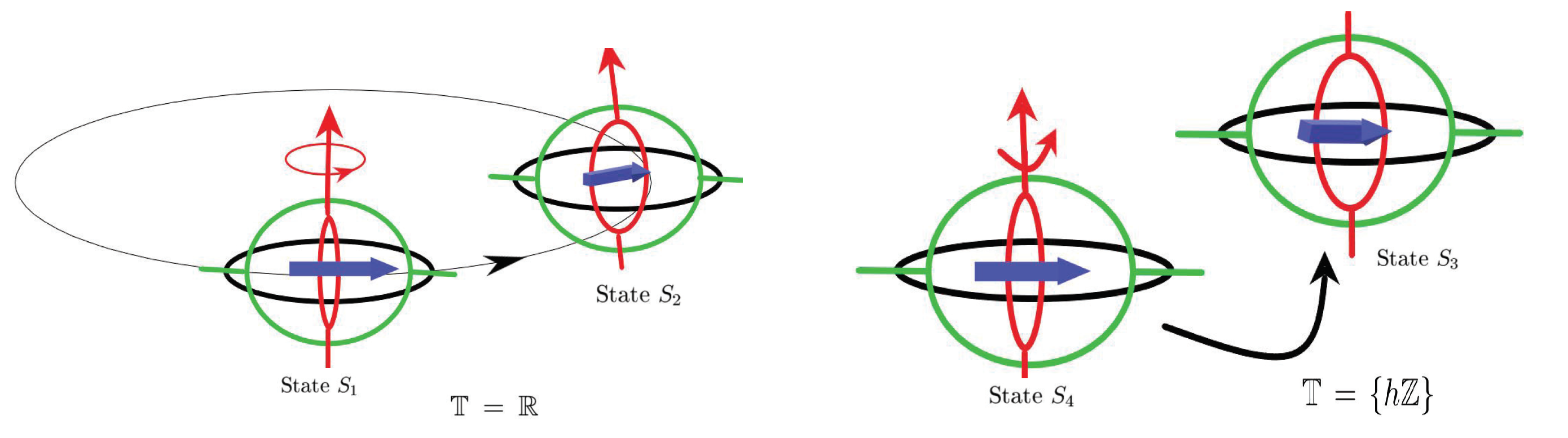
- (1)
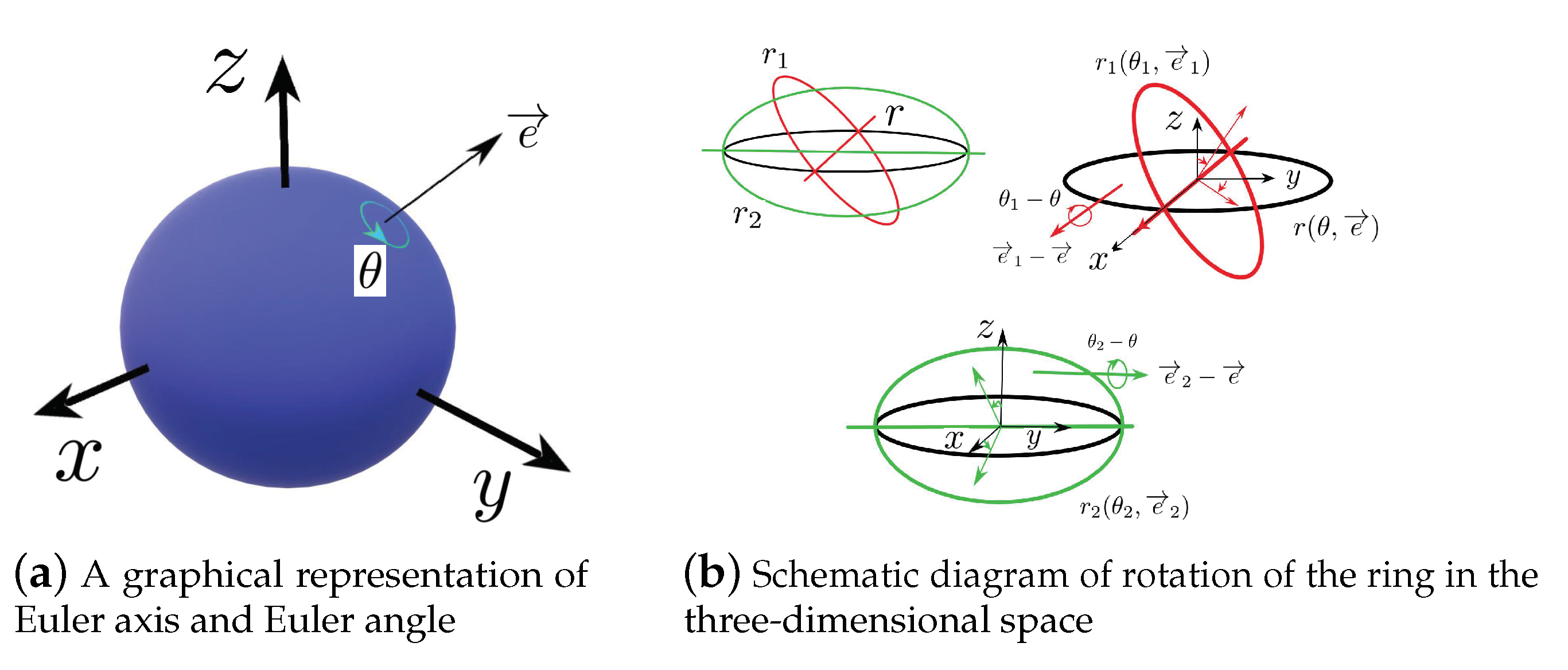
- By Euler’s rotation theory, one can represent a ring rotation through a corresponding quaternion (see Figure 1). However, if a rotation depends on a hybrid time domain, i.e., the ring’s rotation is intermittent, it is reasonable to consider the quaternion-valued functions on a time scale. It is difficult to describe the intermittent rotation by using a quaternion-valued functions on time scales.
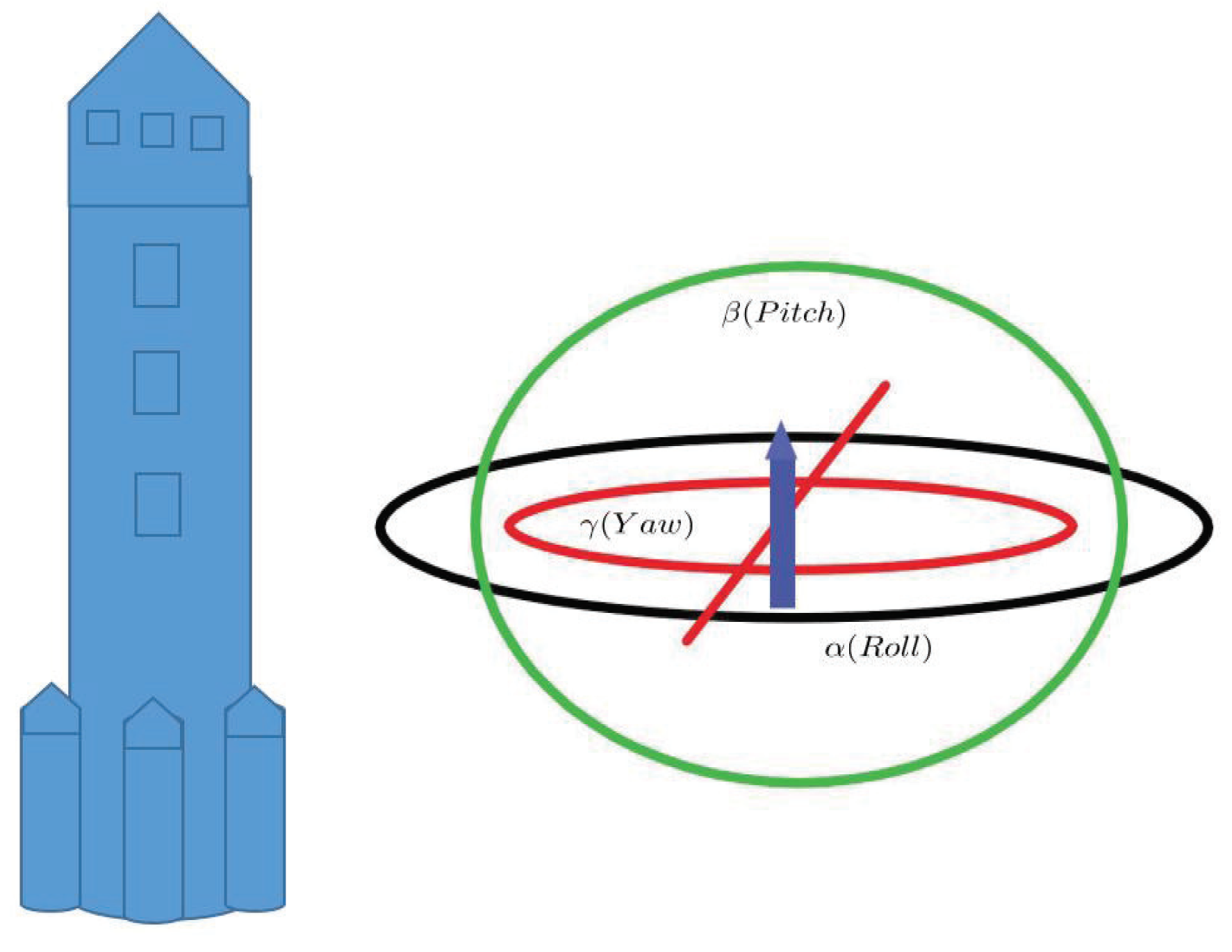
- (2)
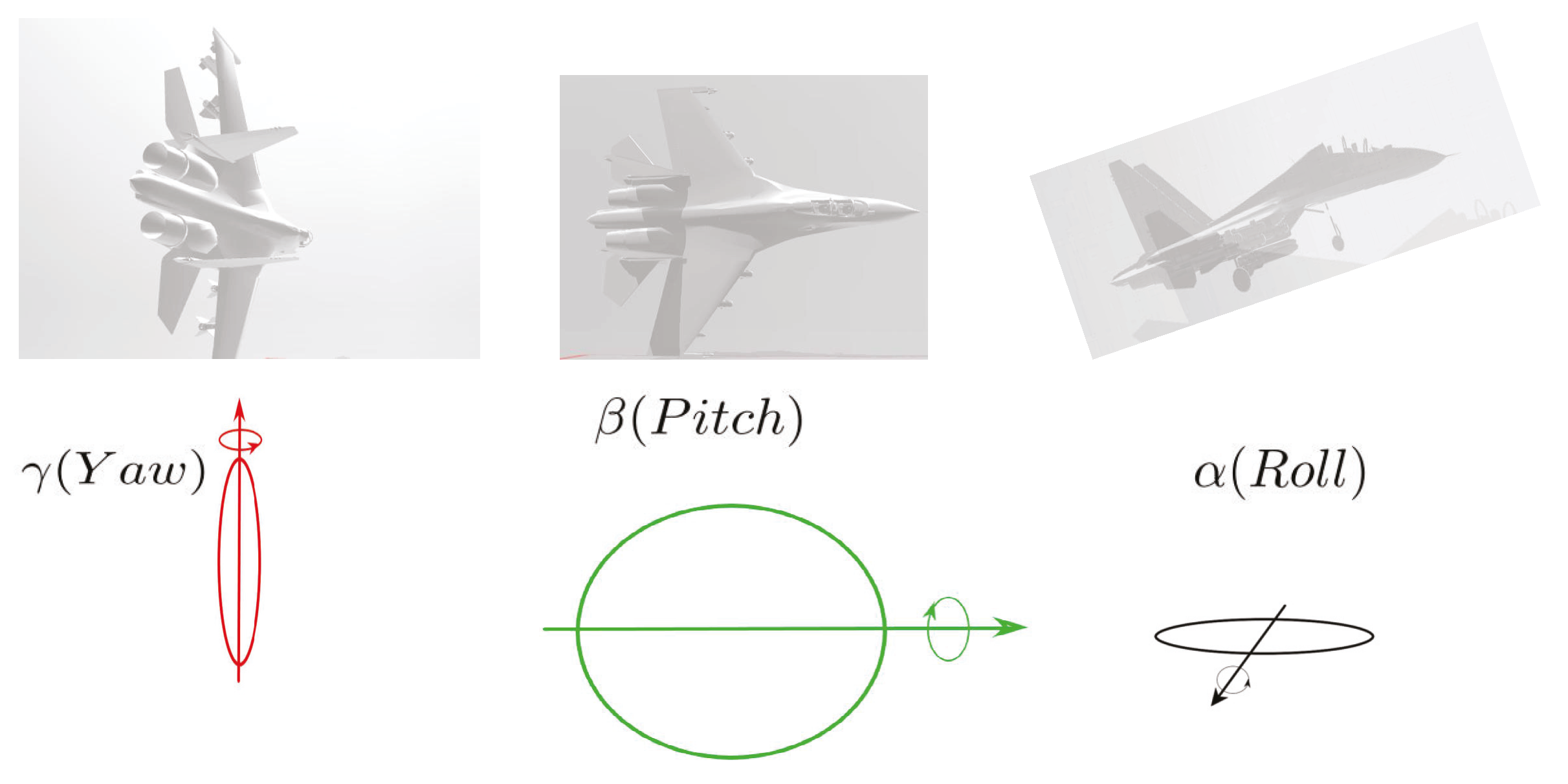
- The direction of many conveyances are controlled by the gyroscope, for example, plane, ship, rocket, etc. The process of their motion is based on a time scale if the gyroscope does not work continuously. How should the work process of the gyroscope controlled by a quaternion dynamic equation be depicted? When does the phenomenon "Gimbal Lock" take place (see Figure 2)? What is expression form of the solution to such quaternion dynamic equations?
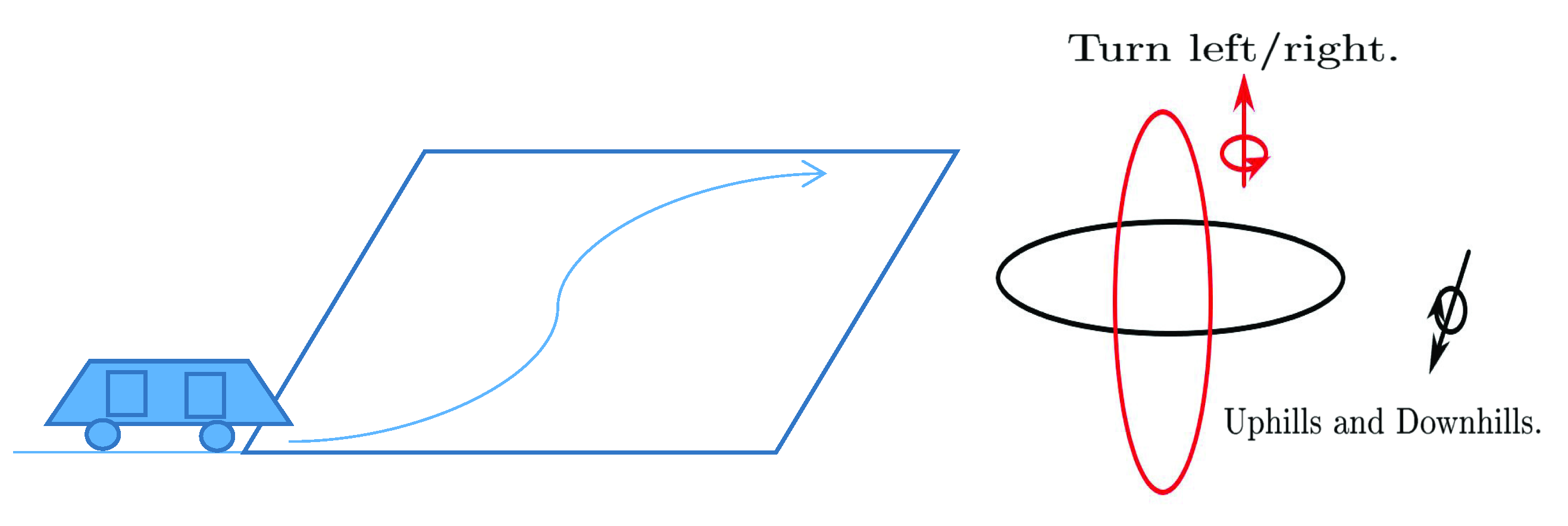
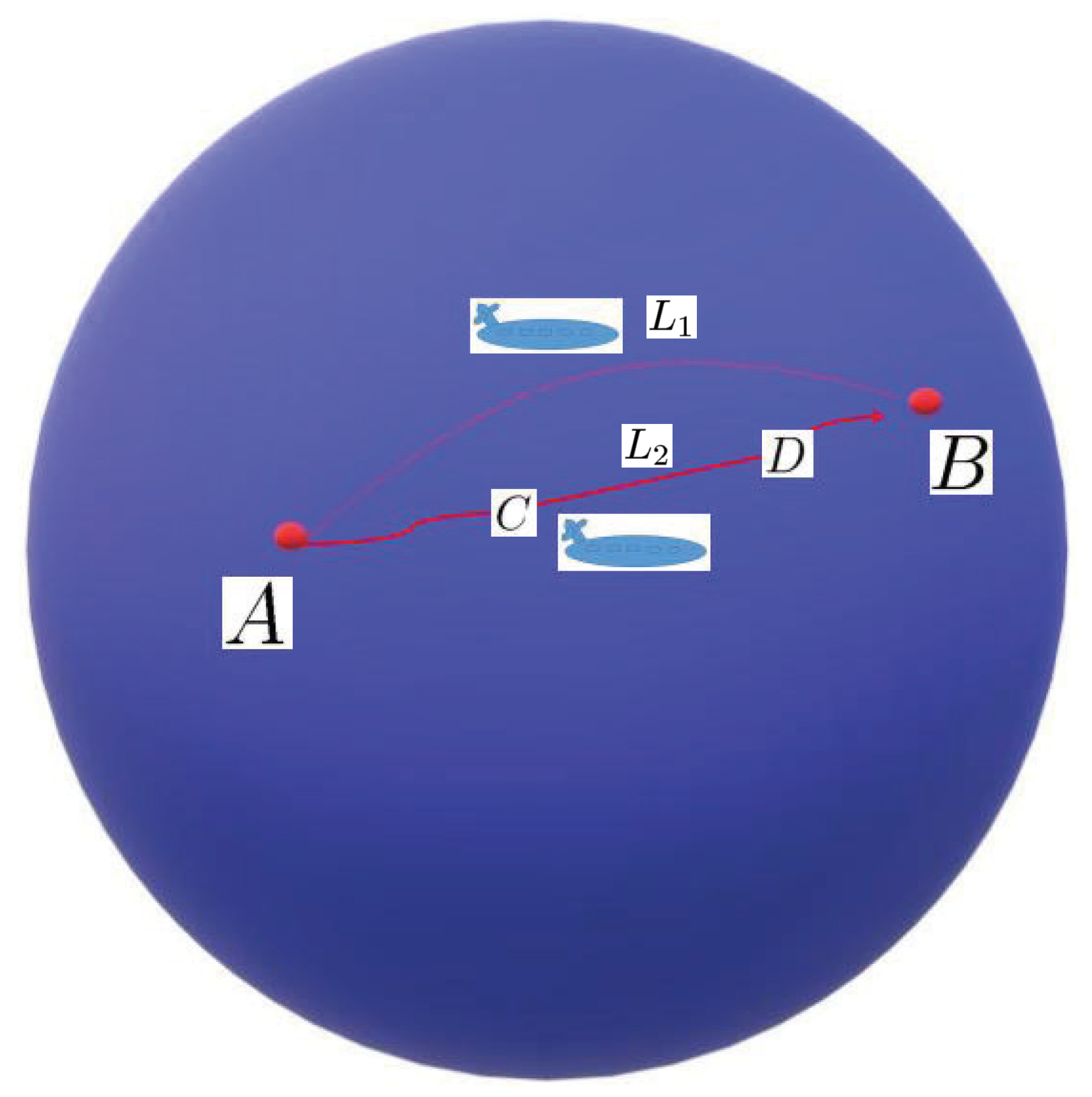
- (3)
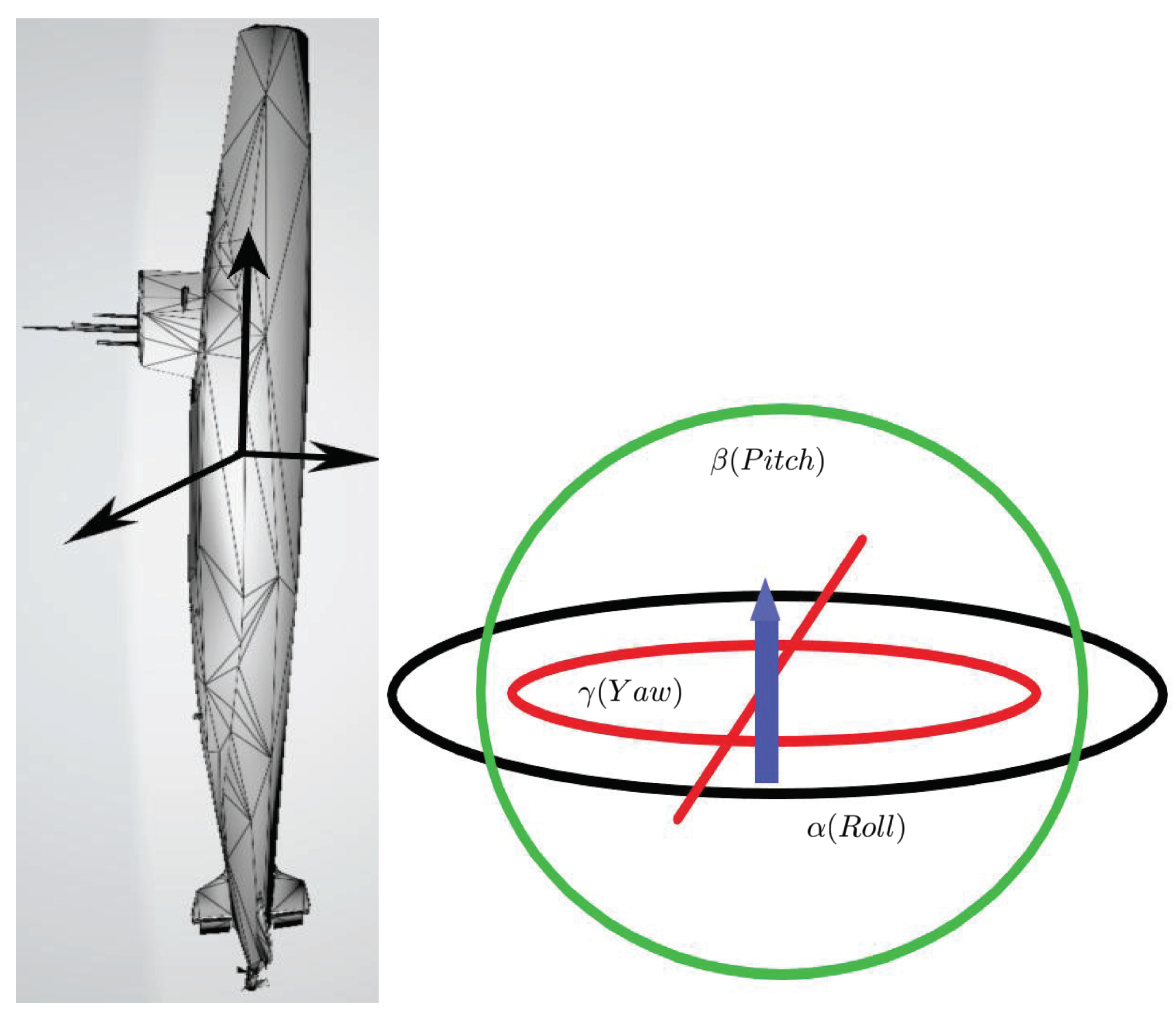
- It is very common to see some phenomena described by a quaternion dynamic equations on time scales. For example, in the process of a car going up a slope, the time that is consumed for changing the direction of the car can be regarded as a time scale which is located in the time interval from the bottom to the top of the hill (see Figure 3). It is convenient to use a quaternion dynamic equations on a time scale to accurately describe the orientations and rotations of the car on the slope. How can a quaternion dynamic equations to describe the process of the orientations and rotations of this car be established? What is the representation form of the solution to this dynamic equations?
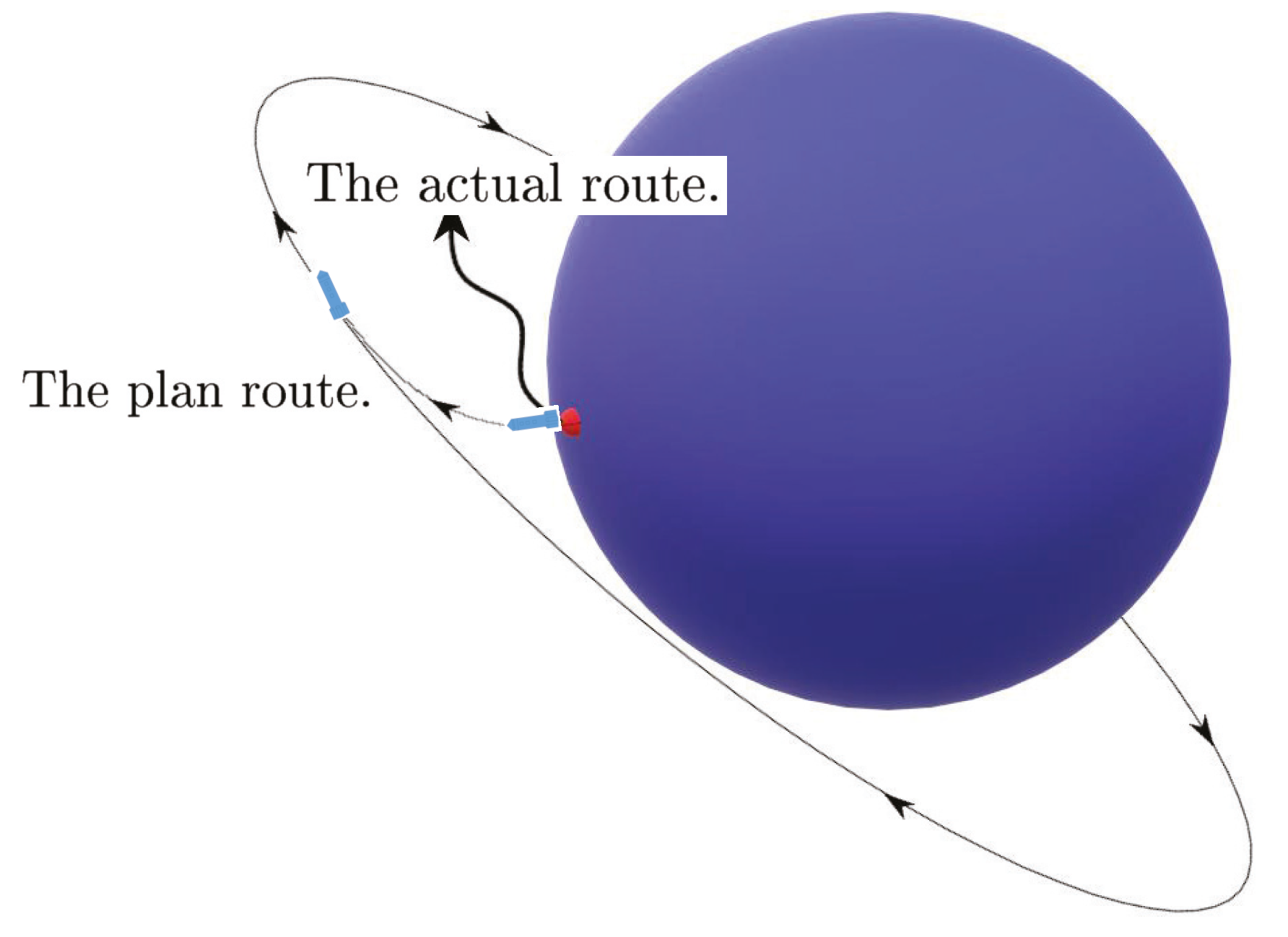
- (4)
- For the dynamic equation with the initial value . The quaternion exponential functionfrom the previous literature is not a solution, this deficiency will lead to a great difficulty to analyze some practical and theoretical problems. For example, the rocket will deviate from its intended route (see Figure 4). Therefore, it is urgent to find the quaternion exponential solution of this initial-valued problem.
- (5)
- As is well known, three rings of the gyroscope work simultaneously such as warplane, rocket (see Figure 5), etc. Unfortunately, it is impossible to depict the orientations and rotations by a quaternion dynamic equations for this case. Hence, it is necessary to consider the higher dimensional matrix quaternion dynamic equations. The main problem is how to establish some basic results of the quaternion dynamic equations based on the double determinant algorithm and extend the case to situation?
- (6)
- Does the linear homogeneous quaternion dynamic equations have a unique solution on time scales? What form does it have? In fact, many objects’ orientations and rotations can be described by quaternion dynamic equations. If the solution is not unique, some reality problems will emerge such as losing the direction of the objects or suffering from the unexpected orientations and rotations.
- (7)
- Letting be a solution of and be a solution of , what are the commutativity conditions of and on time scales? Moreover, what is the connection between the quaternion functions with commutativity conditions and the complex-valued function? What are the commutativity conditions of the quaternion-valued functions on time scales?
- (8)
- Based on the double determinant algorithm, what is the Liouville formula of the linear homogenous quaternion dynamic equations on time scales? Particularly for , what kind of the orientations and rotations phenomena will occur?
- (9)
- We will encounter many problems in real applications in which the or quaternion dynamic equations are not sufficient. Taking the launching rocket as an example, the process will be affected by many factors, for example, the continuously changing earth gravity, the irregular wind power, the predictable and irregular air temperature and the continuously changing atmospheric pressure, etc. All these factors indicate that we must adopt the quaternion dynamic equations on time scales. Therefore, some mathematical questions arise, such as what is the solution expression of the quaternion dynamic equations ? Do these dynamic equations have a unique solution? How can the Liouville formula of the quaternion dynamic equations on time scales be obtained?
4.1. Basic Results of Quaternion Dynamic Equations on Time Scales
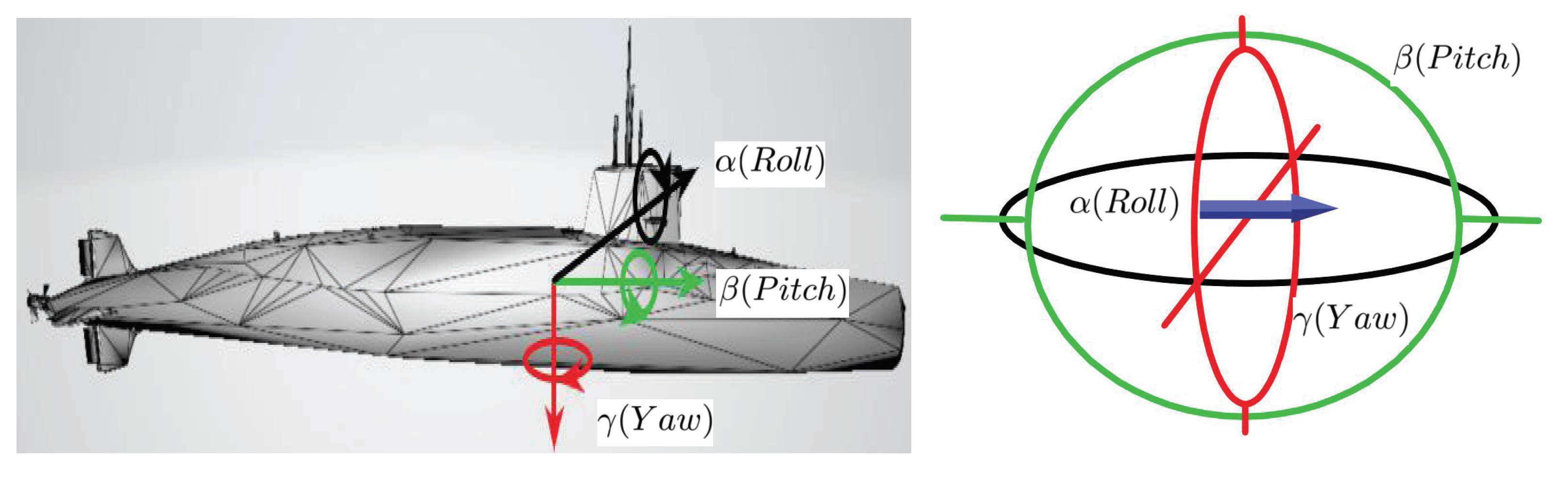
clear syms h11 h21 h31 h12 h22 h32 h13 h23 h33 h14 h24 h34 t; h11=1;h21=1;h31=1;h12=0;h22=0;h32=0;h13=0;h23=0;h33=0;h14=0;h24=0;h34=0; for n=-10:1:4;t=2.^n; h=[h11 h21 h31;h12 h22 h32;h13 h23 h33;h14 h24 h34]; A=[sin(t.^2) cos(t) 0;sin(2.*t) sin(4.*t) 0;1 sin(t) 0]’; B=[sin(t) sin(t + 1) 0;3 4 0;4 0 0]’; C=[sin(2.*t) cos(t) 0;2 1 sin(t);cos(t) sin(2.*t) 0]’; D=[cos(t.^3) sin(t) sin(t);sin(t) 0 0;sin(t) 3 sin(t.^2)]’; h=t.*[h(1,:)*A-h(2,:)*B-h(3,:)*C-h(4,:)*D;h(2,:)*A + h(1,:)*B + h(4,:)*C-h(3,:)*D; h(3,:)*A-h(4,:)*B + h(1,:)*C + h(2,:)*D;h(4,:)*A + h(3,:)*B-h(2,:)*C + h(1,:)*D] + h endThe numerical iteration solution of (38) is given by Table 1. Notice that the existence of solutions to quaternion homogeneous dynamic equations on time scales provides a prerequisite to study the applications of quaternion dynamic equations on various hybrid domains, these significant applications are demonstrated in [61] including the multi-dimensional rotations and transformations of the submarine, gyroscope and planet whose dynamical behaviors are depicted by quaternion dynamics on time scales.
4.2. Applied Quaternion Dynamic Equations
clear syms h11 h21 h12 h22 h13 h23 h14 h24 t; h11=1;h21=1;h12=0;h22=0;h13=0;h23=0;h14=0;h24=0; for n=0:1:14;t=n h=[h11 h21;h12 h22;h13 h23;h14 h24]; A=[15*sin(23.5)*sin(t) 15*sin(t)*sin(t)*sin(23.5); 3.8*sin(t) 3.8*sin(t)*sin(t)]’; B=[15*sin(23.5)*cos(t) 15*cos(t)*sin(t)*sin(23.5); 3.8*cos(t) 3.8*cos(t)*sin(t)]’; C=[15*cos(23.5)*sin(t) 15*sin(t)*cos(t)*cos(23.5);2*sin(t) 2*sin(t)*cos(t)]’; D=[15*sin(23.5)*cos(t) 15*cos(t)*cos(t)*sin(23.5);2*cos(t) 2*cos(t)*cos(t)]’; h=1.*[h(1,:)*A-h(2,:)*B-h(3,:)*C-h(4,:)*D;h(2,:)*A + h(1,:)*B + h(4,:)*C-h(3,:)*D; h(3,:)*A-h(4,:)*B + h(1,:)*C + h(2,:)*D;h(4,:)*A + h(3,:)*B-h(2,:)*C + h(1,:)*D] + h endThe numerical solution of (41) is demonstrated at Table 2. Next, in real application, we will show the solution with the planets corresponding state (see Figure 11), without loss of generality, for , we have
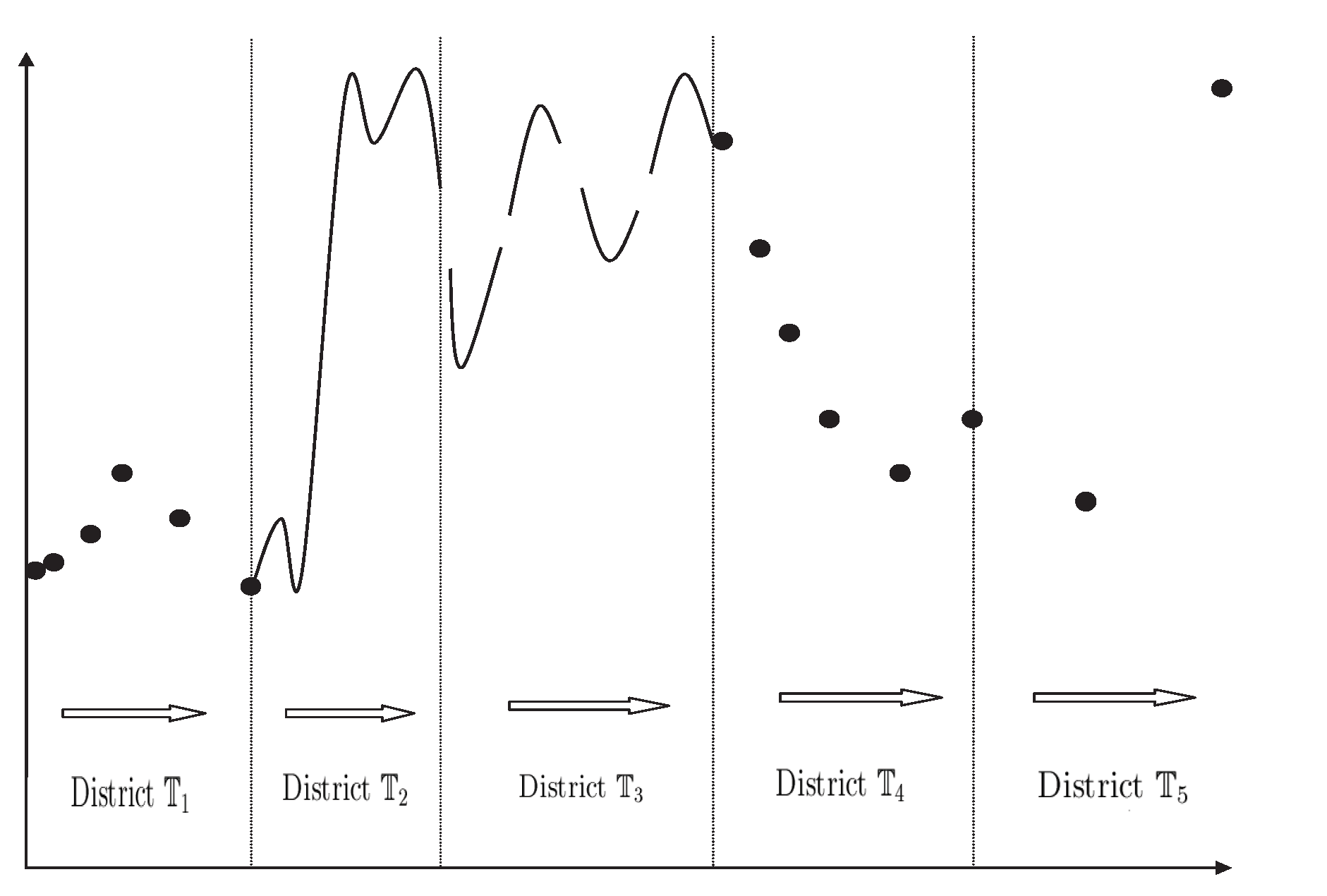
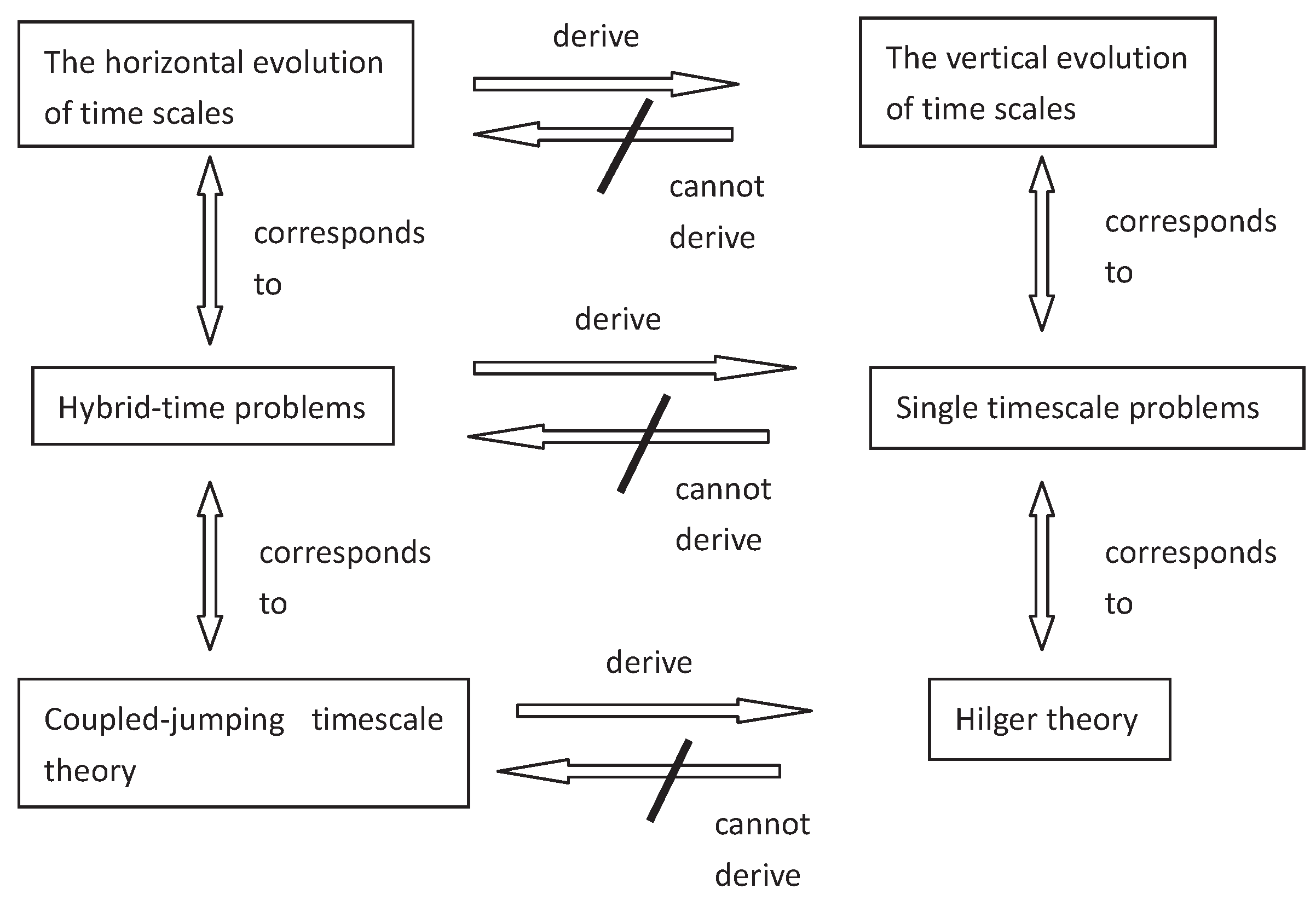
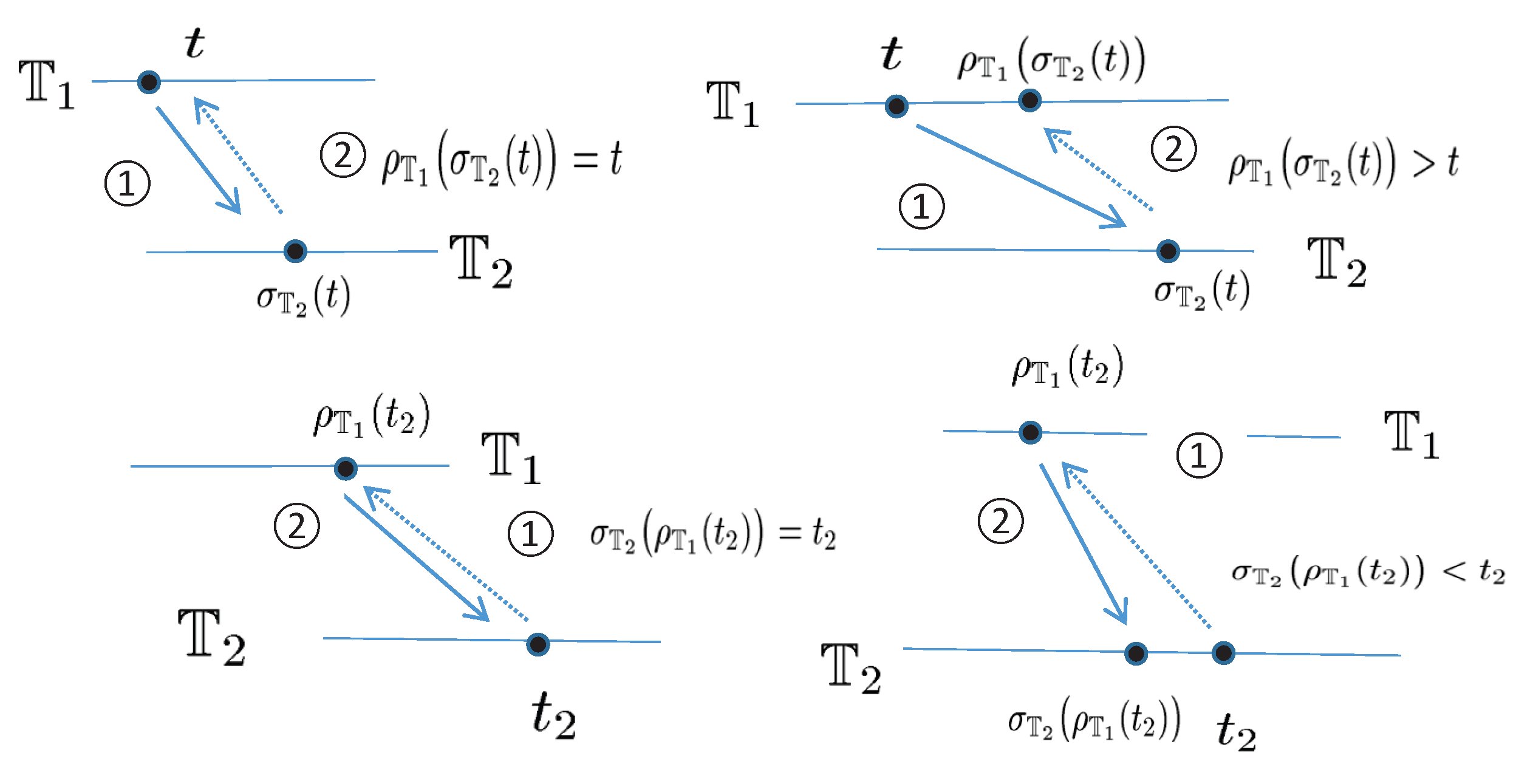
5. The Coupled-Jumping Theory on Time Scales
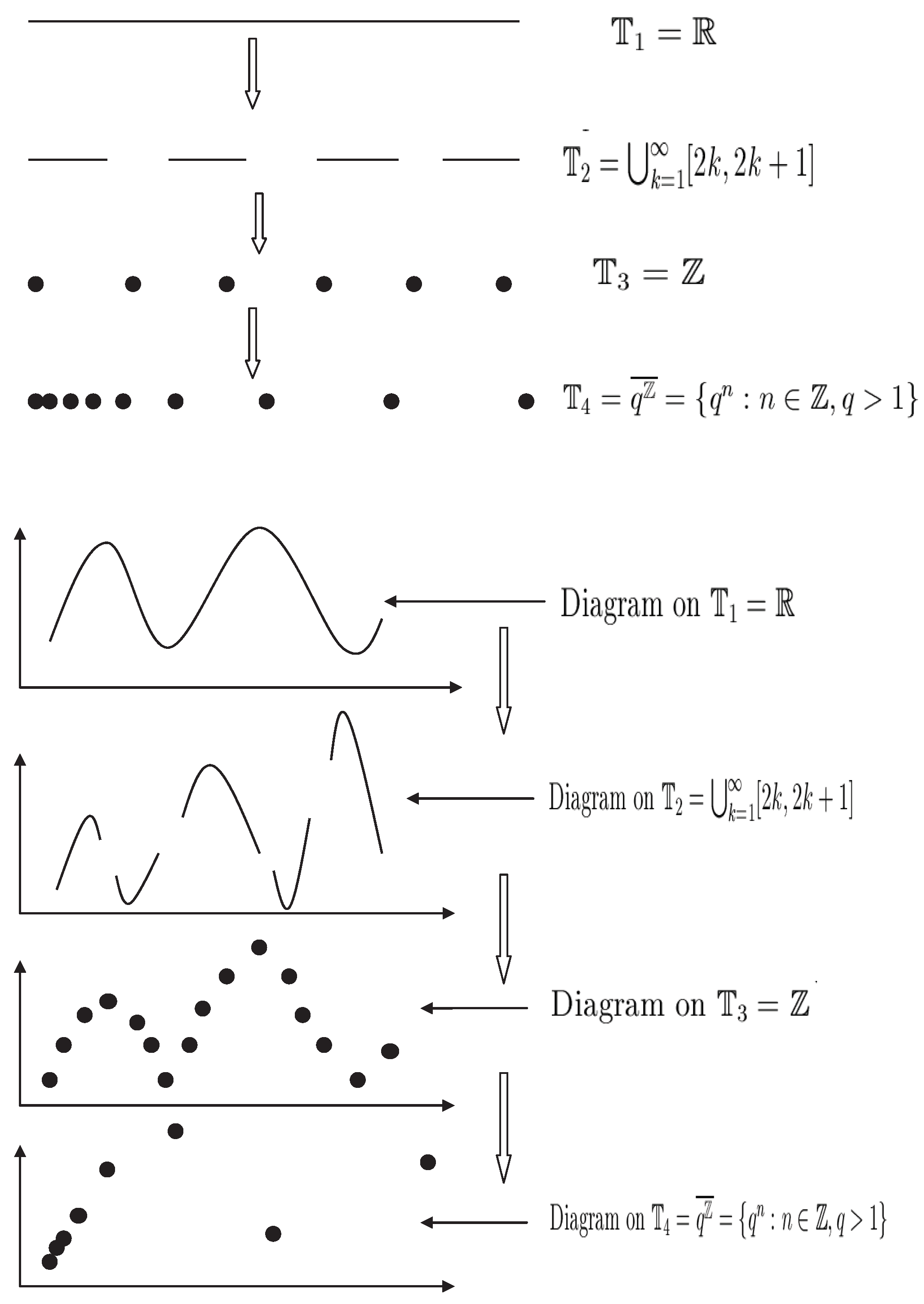
5.1. Vertical Evolution of Time Scales
5.2. Hybrid-Timescale Problems—A Horizontal Evolution of Time Scales
5.3. The Description of the Hybrid-Timescale Initial-Value Problems
5.4. The Coupled-Jumping Timescale Space (CJTS) and Calculus
- (i)
- Let , and . Then, if ; if ;
- (ii)
- ;
- (iii)
- ;
- (iv)
- ;
- (v)
- ;
- (vi)
- if for all .
6. Combined Measure Theory on Time Scales
6.1. -Measurability and -Measure
- (1)
- , if , then ;
- (2)
- let then ;
- (3)
- (i)
- (ii)
- (iii)
- (iv)
6.2. Lebesgue Measurable and Lebesgue -Measurable Sets
- (a)
- (b)
- If E has no scattered points, then
- (c)
- The sets defined in (43) are Lebesgue measurable. Moreover . In addition,where indicates the indices set for all right-scattered and left-dense points, the indices set for all left-scattered and right-dense points, and the indices set for all left-scattered and right-scattered points in E, respectively.
- (d)
- (e)
- if and only if E has no scattered points.
- (i)
- , where and denote the index set of all right-scattered points of E and the index set of all left-scattered points of E, respectively.
- (ii)
- if and only if and E has no scattered points.
- (i)
- , where and denote the index set of all right-scattered points of E and the index set of all left-scattered points of E, respectively.
- (ii)
- if and only if and E has no scattered points.
6.3. Lebesgue–Stieltjes -measurability
- (i)
- ,
- (ii)
- ,
- (iii)
- ,
- (iv)
- If , ,
- (i)
- ,
- (ii)
- ,
- (iii)
- ,
- (iv)
- If , .
- (1)
- Consider the -measure of the above sets:
- 1.
- 2.
- 3.
- (2)
- Consider the -measure of the above sets:
- 1.
- 2.
- 3.
- (2)
- Let , then
- 1.
- ,
- 2.
- ,
- 3.
- ,
- 4.
- For , .
- (3)
- Let and , then -measure turns into -measure as follows:
- 1.
- ,
- 2.
- ,
- 3.
- ,
- 4.
- If , ,
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- , since the limit from the left-hand side of β at is not defined.
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- since the limit from the left-hand side of β at is not defined.
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- since the limit from left-hand side of β at and are not defined.
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hilger, S. Ein Maßkettenkalkül mit Anwendung auf Zentrumsmannigfaltigkeiten. Ph.D. Thesis, Universität Würzburg, Wurzburg, Germany, 1988. [Google Scholar]
- Bohner, M.; Peterson, A. Dynamic Equations on Time Scales An Introduction with Applications; Birkhäuser Boston: Boston, MA, USA, 2001. [Google Scholar]
- Bohner, M.; Peterson, A. Advances in Dynamic Equations on Time Scales; Birkhäuser: Boston, MA, USA, 2003. [Google Scholar]
- Besicovitch, A.S. Almost Periodic Functions; Cambridge University Press: Cambridge, UK, 1932. [Google Scholar]
- Bochner, S. Beitrage zur Theorie der fastperiodischen Funktionen. Math. Annalen 1926, 96, 119–147. [Google Scholar] [CrossRef]
- Bohr, H. Zur Theorie der fastperiodischen Funktionen I. Acta Math. 1925, 45, 29–127. [Google Scholar] [CrossRef]
- Veech, W.A. Almost automorphic functions. Proc. Natl. Acad. Sci. USA 1963, 49, 462–464. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Veech, W.A. Almost Automorphic Functions on Groups. Am. J. Math. 1965, 87, 719–751. [Google Scholar] [CrossRef]
- N’Guérékata, G.M. Almost Automorphic Functions and Almost Periodic Functions in Abstract Spaces; Kluwer: New York, NY, USA, 2001. [Google Scholar]
- N’Guérékata, G.M. Topics in Almost Automorphy; Springer: New York, NY, USA, 2005. [Google Scholar]
- Agarwal, R.P.; Wang, C.; O’Regan, D. Recent development of time scales and related topics on dynamic equations. Mem. Differ. Equ. Math. Phys. 2016, 67, 131–135. [Google Scholar]
- Wang, C.; Agarwal, R.P. Relatively dense sets, corrected uniformly almost periodic functions on time scales, and generalizations. Adv. Differ. Equ. 2015, 312, 1–9. [Google Scholar] [CrossRef]
- Wang, C.; Agarwal, R.P.; O’Regan, D. Periodicity, almost periodicity for time scales and related functions. Nonauton. Dyn. Syst. 2016, 3, 24–41. [Google Scholar] [CrossRef]
- Agarwal, R.P.; O’Regan, D. Some comments and notes on almost periodic functions and changing-periodic time scales. Electr. J. Math. Anal. Appl. 2018, 6, 125–136. [Google Scholar]
- Wang, C. Existence and exponential stability of piecewise mean-square almost periodic solutions for impulsive stochastic Nicholson’s blowflies model on time scales. Appl. Math. Comput. 2014, 248, 101–112. [Google Scholar] [CrossRef]
- Wang, C.; Agarwal, R.P. Uniformly rd-piecewise almost periodic functions with applications to the analysis of impulsive Δ-dynamic system on time scales. Appl. Math. Comput. 2015, 259, 271–292. [Google Scholar]
- Wang, C. Piecewise pseudo almost periodic solution for impulsive non-autonomous highorder Hopfield neural networks with variable delays. Neurocomputing 2016, 171, 1291–1301. [Google Scholar] [CrossRef]
- Wang, C. Almost periodic solutions of impulsive BAM neural networks with variable delays on time scales. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 2828–2842. [Google Scholar] [CrossRef]
- Wang, C.; Agarwal, R.P. Exponential dichotomies of impulsive dynamic systems with applications on time scales. Math. Meth. Appl. Sci. 2015, 38, 3879–3900. [Google Scholar] [CrossRef]
- Wang, C.; Agarwal, R.P. Weighted piecewise pseudo almost automorphic functions with applications to abstract impulsive ∇-dynamic equations on time scales. Adv. Differ. Equ. 2014, 153, 1–29. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Agarwal, R.P.; O’Regan, D. Π-semigroup for invariant under translations time scales and abstract weighted pseudo almost periodic functions with applications. Dyn. Syst. Appl. 2016, 25, 1–28. [Google Scholar]
- Wang, C.; Agarwal, R.P. Almost automorphic functions on semigroups induced by complete-closed time scales and application to dynamic equations. Discret. Contin. Dyn. Syst. B 2020, 25, 781–798. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Agarwal, R.P. A classification of time scales and analysis of the general delays on time scales with applications. Math. Meth. Appl. Sci. 2016, 39, 1568–1590. [Google Scholar] [CrossRef]
- Wang, C.; Agarwal, R.P. A Further study of almost periodic time scales with some notes and applications. Abstr. Appl. Anal. 2014, 2014, 267384. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Agarwal, R.P.; O’Regan, D.; Sakthivel, R. A computation method of Hausdorff distance for translation time scales. Appl. Anal. 2020, 99, 1218–1247. [Google Scholar] [CrossRef]
- Wang, C.; Agarwal, R.P.; O’Regan, D. Weighted piecewise pseudo double-almost periodic solution for impulsive evolution equations. J. Nonlinear Sci. Appl. 2017, 10, 3863–3886. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Sakthivel, R. Double almost periodicity for high-order Hopfield neural networks with slight vibration in time variables. Neurocomputing 2018, 282, 1–15. [Google Scholar] [CrossRef]
- Wang, C.; Agarwal, R.P.; O’Regan, D. Compactness criteria and new impulsive functional dynamic equations on time scales. Adv. Differ. Equ. 2016, 197, 1–41. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Agarwal, R.P.; O’Regan, D. Matrix measure on time scales and almost periodic analysis of the impulsive Lasota-Wazewska model with patch structure and forced perturbations. Math. Meth. Appl. Sci. 2016, 39, 5651–5669. [Google Scholar] [CrossRef]
- Wang, C.; Agarwal, R.P. Almost periodic dynamics for impulsive delay neural networks of a general type on almost periodic time scales. Commun. Nonlinear Sci. Numer. Simulat. 2016, 36, 238–251. [Google Scholar] [CrossRef]
- Wang, C.; Agarwal, R.P.; O’Regan, D.; Sakthivel, R. Discontinuous generalized double-almost-periodic functions on almost-complete-closed time scales. Bound Value Probl. 2019, 165. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Agarwal, R.P. Changing-periodic time scales and decomposition theorems of time scales with applications to functions with local almost periodicity and automorphy. Adv. Differ. Equ. 2015, 296, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Agarwal, R.P.; O’Regan, D.; Sakthivel, R. Theory of Translation Closedness for Time Scales; Developments in Mathematics; Springer: Cham, Switzerland, 2020; Volume 62. [Google Scholar]
- Wang, C.; Agarwal, R.P.; O’Regan, D. Local-periodic solutions for functional dynamic equations with infinite delay on changing-periodic time scales. Math. Slovaca 2018, 68, 1397–1420. [Google Scholar] [CrossRef]
- Wang, C.; Agarwal, R.P.; O’Regan, D.; Sakthivel, R. Local pseudo almost automorphic functions with applications to semilinear dynamic equations on changing-periodic time scales. Bound Value Probl. 2019, 133. [Google Scholar] [CrossRef]
- Wang, C.; Agarwal, R.P.; O’Regan, D. A matched space for time scales and applications to the study on functions. Adv. Differ. Equ. 2017, 305, 1–28. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Agarwal, R.P.; O’Regan, D. The shift invariance of time scales and applications. In Proceedings of the International Workshop QUALITDE-2017, Tbilisi, Georgia, 4–26 December 2017. [Google Scholar]
- Wang, C.; Agarwal, R.P.; O’Regan, D. n0-order Δ-almost periodic functions and dynamic equations. Applic. Anal. 2018, 97, 2626–2654. [Google Scholar] [CrossRef]
- Wang, C.; Agarwal, R.P.; O’Regan, D. δ-almost periodic functions and applications to dynamic equations. Mathematics 2019, 7, 525. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Agarwal, R.P.; O’Regan, D. Weighted pseudo δ-almost automorphic functions and abstract dynamic equations. Georgian Math. J. 2019, in press. [Google Scholar] [CrossRef]
- Wang, C.; Agarwal, R.P.; O’Regan, D.; N’Guérékata, G.M. n0-Order weighted pseudo Δ-almost automorphic functions and abstract dynamic equations. Mathematics 2019, 7, 775. [Google Scholar] [CrossRef] [Green Version]
- Anirban, A. Fuzzy graphene for neuron control. Nat. Rev. Phys. 2020, 2, 344. [Google Scholar] [CrossRef]
- Balachandran, A.P.; Kürkçüoglu, S.; Vaidya, S. Lectures on Fuzzy and Fuzzy SUSY Physics; World Scientific: Singapore, 2007. [Google Scholar]
- Jarosław, P. Quantum Physics, Fuzzy Sets and Logic, Steps Towards a Many-Valued Interpretation of Quantum Mechanics; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Madore, J. Fuzzy physics. Ann. Phys. 1992, 219, 187–198. [Google Scholar] [CrossRef]
- Adívar, M. A new periodic concept for time scales. Math. Slovaca 2013, 63, 817–828. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Agarwal, R.P.; Sakthivel, R. Almost periodic oscillations for delay impulsive stochastic Nicholson’s blowflies timescale model. Comput. Appl. Math. 2018, 37, 3005–3026. [Google Scholar] [CrossRef]
- Wang, C.; Agarwal, R.P. Almost periodic solution for a new type of neutral impulsive stochastic Lasota-Wazewska timescale model. Appl. Math. Lett. 2017, 70, 58–65. [Google Scholar] [CrossRef]
- Wang, C.; Sakthivel, R.; N’Guérékata, G.M. S-almost automorphic solutions for impulsive evolution equations on time scales in shift operators. Mathematics 2020, 8, 1028. [Google Scholar] [CrossRef]
- Wang, C.; Agarwal, R.P.; O’Regan, D. Calculus of fuzzy vector-valued functions and almost periodic fuzzy vector-valued functions on time scales. Fuzzy Sets Syst. 2019, 375, 1–52. [Google Scholar] [CrossRef]
- Bohner, M.; Stanzhytskyi, O.M.; Bratochkina, A.O. Stochastic dynamic equations on general time scales. Electron. J. Differ. Equ. 2013, 57, 1–15. [Google Scholar]
- Bede, B. Mathematics of Fuzzy Sets and Fuzzy Logic; Studies in Fuzziness and Soft Computing, 295; Springer: Heidelberg, Germany, 2013. [Google Scholar]
- Stefanini, L. A generalization of Hukuhara difference and division for interval and fuzzy arithmetic. Fuzzy Sets Syst. 2010, 161, 1564–1584. [Google Scholar] [CrossRef]
- Katz, A. Computational Rigid Vehicle Dynamics; Krieger Publishing Co.: Malabar, FL, USA, 1996. [Google Scholar]
- Kuipers, J.B. Quaternions and rotation Sequences: A Primer with Applications to Orbits, Aerospace, and Virtual Reality; Princeton University Press: Princeton, NJ, USA, 1999. [Google Scholar]
- McCarthy, J.M. Introduction to Theoretical Kinematics; MIT Press: Cambridge, MA, USA, 1990. [Google Scholar]
- Shoemake, K. Animating Rotation with Quaternion Curves. Comput. Graph. 1985, 19, 245–254. [Google Scholar] [CrossRef]
- Cheng, D.; Kou, K.I.; Xia, Y. A unified analysis of linear quaternion dynamic equations on time scales. J. Appl. Anal. Comput. 2018, 8, 172–201. [Google Scholar]
- Kou, K.I.; Xia, Y. Linear quaternion differential equations: Basic theory and fundamental results. Studies. Appl. Math. 2018, 141, 3–45. [Google Scholar] [CrossRef]
- Li, Z.; Wang, C. Cauchy matrix and Liouville formula of quaternion impulsive dynamic equations on time scales. Open Math. 2020, 18, 353–377. [Google Scholar] [CrossRef]
- Li, Z.; Wang, C.; Agarwal, R.P.; O’Regan, D. Commutativity of quaternion-matrix-valued functions and quaternion matrix dynamic equations on time scales. Stud. Appl. Math. 2021, 146, 139–210. [Google Scholar] [CrossRef]
- Wang, C.; Li, Z.; Agarwal, R.P.; O’Regan, D. Coupled-jumping timescale theory and applications to time-hybrid dynamic equations, convolution and Laplace transforms. Dyn. Syst. Appl. 2021, 30, 461–508. [Google Scholar]
- Wang, C.; Agarwal, R.P.; O’Regan, D. Coupled-Jumping Timescale Theory and Applications. In Proceedings of the International Workshop QUALITDE-2020, Tbilisi, Georgia, 19–21 December 2020; pp. 203–208. [Google Scholar]
- Deniz, A.; Ufuktepe, Ü. Lebesgue–Stieltjes measure on time scales. Turk. J. Math. 2009, 33, 27–40. [Google Scholar]
- Deniz, A. Measure Theory on Time Scales. Master’s Thesis, Graduate School of Engineering and Sciences of Izmir Institute of Technology, Izmir, Turkey, 2007. [Google Scholar]
- Sheng, Q.; Fadag, M.; Henderson, J.; Davis, J.M. An exploration of combined dynamic derivatives on time scales and their applications. Nonlinear Anal. Real World Appl. 2006, 7, 395–413. [Google Scholar] [CrossRef]
- Li, Z.; Wang, C.; Agarwal, R.P. The non-eigenvalue form of Liouville’s formula and α-matrix exponential solutions for combined matrix dynamic equations on time scales. Mathematics 2019, 7, 962. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Qin, G.; Agarwal, R.P.; O’Regan, D. ⋄α-Measurability and combined measure theory on time scales. Appl. Anal. 2020, in press. [Google Scholar] [CrossRef]
- Qin, G.; Wang, C. Lebesgue–Stieltjes combined ⋄α-measure and integral on time scales. Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Mat. RACSAM 2021, 115, 50. [Google Scholar] [CrossRef]





| t | |||||||||||||
| 9.7656 × 10−4 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0.0020 | 1.0010 | 1.0000 | 1.0010 | 0.0008 | 0.0068 | 0.0039 | 0.0010 | 0.0029 | 0.0010 | 0.0010 | 0.0000 | 0.0029 | |
| 0.0039 | 1.0020 | 1.0000 | 1.0020 | 0.0016 | 0.0137 | 0.0078 | 0.0020 | 0.0059 | 0.0020 | 0.0020 | 0.0000 | 0.0059 | |
| 0.0078 | 1.0039 | 1.0001 | 1.0039 | 0.0033 | 0.0273 | 0.0156 | 0.0039 | 0.0117 | 0.0039 | 0.0039 | 0.0000 | 0.0117 | |
| 0.0156 | 1.0078 | 1.0004 | 1.0079 | 0.0067 | 0.0547 | 0.0313 | 0.0079 | 0.0235 | 0.0079 | 0.0079 | 0.0001 | 0.0235 | |
| 0.0313 | 1.0156 | 1.0015 | 1.0159 | 0.0135 | 0.1094 | 0.0625 | 0.0161 | 0.0471 | 0.0161 | 0.0161 | 0.0002 | 0.0471 | |
| 0.0625 | 1.0313 | 1.0058 | 1.0322 | 0.0278 | 0.2188 | 0.1250 | 0.0332 | 0.0947 | 0.0332 | 0.0332 | 0.0010 | 0.0948 | |
| 0.1250 | 1.0626 | 1.0233 | 1.0664 | 0.0585 | 0.4375 | 0.2500 | 0.0702 | 0.1914 | 0.0702 | 0.0703 | 0.0039 | 0.1916 | |
| 0.2500 | 1.1260 | 1.0909 | 1.1406 | 0.1284 | 0.8750 | 0.5000 | 0.1550 | 0.3906 | 0.1550 | 0.1562 | 0.0156 | 0.3925 | |
| 0.5000 | 1.2578 | 1.3302 | 1.3119 | 0.2991 | 1.7500 | 1.0000 | 0.3621 | 0.8119 | 0.3621 | 0.3737 | 0.0619 | 0.8275 | |
| 1 | 1.5625 | 1.8754 | 1.7397 | 0.7385 | 3.5000 | 2.0000 | 0.8595 | 1.7397 | 0.8595 | 0.9755 | 0.2397 | 1.8634 | |
| 2 | 2.3818 | 1.1525 | 2.8415 | 1.7508 | 7.0000 | 4.0000 | 1.4496 | 3.8415 | 1.4496 | 2.2232 | 0.8415 | 4.6829 | |
| 4 | −1.3459 | 1.4651 | 4.8186 | 2.1008 | 14.0000 | 8.0000 | −2.3459 | 7.8186 | −2.3459 | 3.3462 | 1.8186 | 6.3050 | |
| 8 | −2.7662 | 3.8058 | 1.9728 | −6.8629 | 28.0000 | 16.0000 | 1.3429 | 8.9728 | 1.3429 | −4.4870 | −3.0272 | 7.8212 | |
| 16 | 7.1962 | 3.1082 | 16.9149 | 11.2118 | 56.0000 | 32.0000 | −3.4672 | 31.9149 | −3.4672 | 7.8551 | 7.9149 | 39.2751 | |
| 32 | −30.3099 | 24.5432 | 12.3935 | −19.9888 | 112.0000 | 64.0000 | −6.4997 | 43.3935 | −6.4997 | 3.6509 | −4.6065 | 27.4062 | |
| t | |||||||||||||
| 0 | 9.7656 × 10−4 | 1 | 1 | 1 | |||||||||
| 1 | 0.0020 | 1.0010 + 0.0008i + 0.0010j + 0.0010k | 1.0000 + 0.0068i + 0.0029j + 0.0000k | 1.0010 + 0.0039i + 0.0010j + 0.0029k | |||||||||
| 2 | 0.0039 | 1.0020 + 0.0016i + 0.0020j + 0.0020k | 1.0000 + 0.0137i + 0.0059j + 0.0000k | 1.0020 + 0.0078i + 0.0020j + 0.0059k | |||||||||
| 3 | 0.0078 | 1.0039 + 0.0033i + 0.0039j + 0.0039k | 1.0001 + 0.0273i + 0.0117j + 0.0000k | 1.0039 + 0.0156i + 0.0039j + 0.0117k | |||||||||
| 4 | 0.0156 | 1.0078 + 0.0067i + 0.0079j + 0.0079k | 1.0004 + 0.0547i + 0.0235j + 0.0001k | 1.0079 + 0.0313i + 0.0079j + 0.0235k | |||||||||
| 5 | 0.0313 | 1.0156 + 0.0135i + 0.0161j + 0.0161k | 1.0015 + 0.1094i + 0.0471j + 0.0002k | 1.0159 + 0.0625i + 0.0161j + 0.0471k | |||||||||
| 6 | 0.0625 | 1.0313 + 0.0278i + 0.0332j + 0.0332k | 1.0058 + 0.2188i + 0.0947j + 0.0010k | 1.0322 + 0.1250i + 0.0332j + 0.0948k | |||||||||
| 7 | 0.1250 | 1.0626 + 0.0585i + 0.0702j + 0.0703k | 1.0233 + 0.4375i + 0.1914j + 0.0039k | 1.0664 + 0.2500i + 0.0702j + 0.1916k | |||||||||
| 8 | 0.2500 | 1.1260 + 0.1284i + 0.1550j + 0.1562k | 1.0909 + 0.8750i + 0.3906j + 0.0156k | 1.1406 + 0.5000i + 0.1550j + 0.3925k | |||||||||
| 9 | 0.5000 | 1.2578 + 0.2991i + 0.3621j + 0.3737k | 1.3302 + 1.7500i + 0.8119 j + 0.0619jk | 1.3119 + 1.0000i + 0.3621j + 0.8275k | |||||||||
| 10 | 1 | 1.5625 + 0.7385i + 0.8595j + 0.9755k | 1.8754 + 3.5000i + 1.7397j + 0.2397k | 1.7397 + 2.0000i + 0.8595j + 1.8634k | |||||||||
| 11 | 2 | 2.3818 + 1.7508i + 1.4496j + 2.2232k | 1.1525 + 7.0000i + 3.8415j + 0.8415k | 2.8415 + 4.0000i + 1.4496j + 4.6829k | |||||||||
| 12 | 4 | −1.3459 + 2.1008i− 2.3459j + 3.3462k | 1.4651 + 14.0000i + 7.8186j + 1.8186k | 4.8186 + 8.0000i− 2.3459j + 6.3050k | |||||||||
| 13 | 8 | −2.7662 − 6.8629i + 1.3429j− 4.4870k | 3.8058 + 28.0000i + 8.9728j− 3.0272k | 1.9728 + 16.0000i + 1.3429j + 7.8212k | |||||||||
| 14 | 16 | 7.1962 + 11.2118i− 3.4672j + 7.8551k | 3.1082 + 56.0000i + 31.9149j + 7.9149k | 16.9149 + 32.0000i− 3.4672j + 39.2751k | |||||||||
| 15 | 32 | −30.3099 − 19.9888i− 6.4997j + 3.6509k | 24.5432 + 112.0000i + 43.3935j− 4.6065k | 12.3935 + 64.0000i− 6.4997j + 27.4062k | |||||||||
| t | |||||||||
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1.0000 | 1.0000 | −14.9712 | 3.8000 | 0 | 0 | −29.9425 | 4.0000 |
| 2 | 2 | −22.1986 | 6.8883 | −14.8956 | 3.7808 | −1.2036 | 2.5922 | −12.4595 | 1.6645 |
| 3 | 3 | −24.9918 | 7.5973 | 11.8954 | −3.0193 | −0.4930 | 1.0618 | 3.6375 | −0.4859 |
| 4 | 4 | −1.4109 | 1.6119 | 16.9130 | −4.2929 | −0.0013 | 0.0028 | 0.1483 | −0.0198 |
| 5 | 5 | 3.7555 | 0.3006 | 2.3799 | −0.6041 | 0.2434 | −0.5242 | 3.3894 | −0.4528 |
| 6 | 6 | 1.5897 | 0.8503 | −0.1744 | 0.0443 | 1.1430 | −2.4619 | −5.4514 | 0.7283 |
| 7 | 7 | 4.0143 | 0.2349 | -10.3584 | 2.6292 | 0.5086 | −1.0954 | −28.1773 | 3.7642 |
| 8 | 8 | −15.2980 | 5.1367 | −18.7021 | 4.7470 | −1.0700 | 2.3046 | −19.7960 | 2.6445 |
| 9 | 9 | −28.4662 | 8.4791 | 4.3334 | −1.0999 | −0.7850 | 1.6908 | 1.8614 | −0.2487 |
| 10 | 10 | −7.7127 | 3.2114 | 19.2623 | −4.8892 | −0.0340 | 0.0732 | 1.2122 | −0.1619 |
| 11 | 11 | 4.7138 | 0.0574 | 5.7280 | −1.4539 | 0.0813 | −0.1751 | 2.0216 | −0.2701 |
| 12 | 12 | 1.0001 | 1.0000 | −0.0000 | 0.0000 | 0.9327 | −2.0088 | −0.0666 | 0.0089 |
| 13 | 13 | 4.7228 | 0.0551 | −5.8547 | 1.4860 | 0.9187 | −1.9787 | −23.2944 | 3.1119 |
| 14 | 14 | −7.9334 | 3.2675 | −19.2938 | 4.8972 | 7 − 0.7442 | 1.6029 | −25.9138 | 3.4618 |
| 15 | 15 | −28.5219 | 8.4933 | −4.0750 | 1.0343 | −1.0456 | 2.2521 | −2.3270 | 0.3109 |
| t | |||||||||
| 0 | 0 | 1 | 1 | ||||||
| 1 | 1 | 1.0000 − 14.9712i− 29.9425k | 1.0000 + 3.8000i + 4.0000k | ||||||
| 2 | 2 | −22.1986 − 14.8956i− 1.2036j− 12.4595k | 6.8883 + 3.7808i + 2.5922j + 1.6645k | ||||||
| 3 | 3 | −24.9918 + 11.8954i− 0.4930j + 3.6375k | 7.5973 − 3.0193i + 1.0618j− 0.4859k | ||||||
| 4 | 4 | −1.4109 + 16.9130i− 0.0013j + 0.1483k | 1.6119 − 4.2929i + 0.0028j− 0.0198k | ||||||
| 5 | 5 | 3.7555 + 2.3799i + 0.2434j + 3.3894k | 0.3006 − 0.6041i− 0.5242j− 0.4528k | ||||||
| 6 | 6 | 1.5897 − 0.1744i + 1.1430j− 5.4514k | 0.8503 + 0.0443i− 2.4619j + 0.7283k | ||||||
| 7 | 7 | 4.0143 −10.3584i + 0.5086j− 28.1773k | 0.2349 + 2.6292i− 1.0954j + 3.7642k | ||||||
| 8 | 8 | −15.2980 − 18.7021i− 1.0700j− 19.7960k | 5.1367 + 4.7470i + 2.3046j + 2.6445k | ||||||
| 9 | 9 | −28.4662 + 4.3334i− 0.7850j + 1.8614k | 8.4791 − 1.0999i + 1.6908j− 0.2487k | ||||||
| 10 | 10 | −7.7127 + 19.2623i− 0.0340j + 1.2122k | 3.2114 − 4.8892i + 0.0732j− 0.1619k | ||||||
| 11 | 11 | 4.7138 + 5.7280i + 0.0813j + 2.0216k | 0.0574 − 1.4539i− 0.1751j− 0.2701k | ||||||
| 12 | 12 | 1.0001 − 0.0000i + 0.9327j− 0.0666k | 1.0000 + 0.0000i− 2.0088j + 0.0089k | ||||||
| 13 | 13 | 4.7228 − 5.8547i + 0.9187j− 23.2944k | 0.0551 + 1.4860i− 1.9787j + 3.1119k | ||||||
| 14 | 14 | −7.9334 − 19.2938i− 0.7442j− 25.9138k | 3.2675 + 4.8972i + 1.6029j + 3.4618k | ||||||
| 15 | 15 | −28.5219 − 4.0750i− 1.0456j− 2.3270k | 8.4933 + 1.0343i + 2.2521j + 0.3109k | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Agarwal, R.P. A Survey of Function Analysis and Applied Dynamic Equations on Hybrid Time Scales. Entropy 2021, 23, 450. https://0-doi-org.brum.beds.ac.uk/10.3390/e23040450
Wang C, Agarwal RP. A Survey of Function Analysis and Applied Dynamic Equations on Hybrid Time Scales. Entropy. 2021; 23(4):450. https://0-doi-org.brum.beds.ac.uk/10.3390/e23040450
Chicago/Turabian StyleWang, Chao, and Ravi P. Agarwal. 2021. "A Survey of Function Analysis and Applied Dynamic Equations on Hybrid Time Scales" Entropy 23, no. 4: 450. https://0-doi-org.brum.beds.ac.uk/10.3390/e23040450







