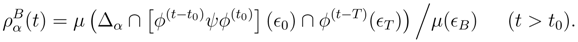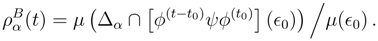1 Introduction
The manifest asymmetry of past and future was a subject of inquiry long before developments in physical theory enhanced the puzzle through an apparent conflict with the nearly symmetric microscopic laws of physics. This “manifest” asymmetry is sometimes called the psychological arrow of time or the consciousness arrow or the biological arrow [
1]. Its characterizations are as diverse as its definition is difficult. One common theme is that the past is
over, complete, immutable; the future is open to change. Mostly, physicists stick to more clear-cut asymmetries, for example in the Second Law of Thermodynamics (the thermodynamic arrow), the expansion of the universe (the cosmological arrow) or certain microscopic laws of physics (the CP arrow). My own opinion, shared by others, is that the psychological arrow is a consequence of the thermodynamic arrow. I view our psychological processes as an outgrowth of other biological processes and I find no reason to propose an arrow for digestion that is not already covered by that describing other chemical processes, specifically the thermodynamic arrow. See Ref. [
2].
Unfortunately, it is difficult to defend this position with anything more than hand-waving arguments. Partly, subtleties in the definition of the thermodynamic arrow get in the way, but more of an obstacle is the intrusion of issues like consciousness, life, free will, and possible indeterminism. In this article I will show that a contemporary computer has features that parallel the psychological arrow of time. I do not claim that this proves the assertion made in my first paragraph. In fact I expect that no one who does not already agree with me will find my analogies compelling. What I hope to do though is to see how much can be said before coming to “undebatable” issues (in the sense that no one ever convinces anyone else) like reductionism.
In
Sec. 2 the form of the thermodynamic arrow to be used is presented including its implications for the distinction between prediction and retrodiction (the mathematical details are not essential to the sequel). Next I develop a characterization of a computer.
Sec. 4 discusses computer properties that parallel our own psychological arrow. The final Section explicitly states the claimed relationship as well as expresses some reservations.
2 The thermodynamic arrow: causality and entropy increase
The thermodynamic arrow is here defined as a kind of causality. Let t be a neutral dynamical time parameter having no a priori thermodynamic directionality. Consider several identically prepared macroscopic systems that are isolated during the time intervals [0, t0] and [t0, t1] (0 < t0 < t1), and let them be struck by a variety of outside forces at t0. For a thermodynamic arrow whose direction is in the direction of increasing “t” their behavior in the interval [0, t0] will be identical, but will be different in the interval [t0, t1]. This arrow can also be characterized as the use of initial conditions for macroscopic problems. The choice of which direction of the parameter t is to be considered “initial’ is the arrow. This is essentially equivalent to the usual statements about entropy increase or the forbidding of the conversion of heat to work.
As shown in Ref. [
3], both macroscopic causality and entropy increase can be derived within a larger time-symmetric context. An outline of the reasoning follows. For simplicity only a limited range of classical dynamical systems is presented.
The dynamics takes place on a phase space, Ω, with measure
µ, and is given by a family of invertible measure-preserving maps,
ϕ(t), −∞ < t < ∞. The coarse graining, necessary to define “macroscopic” as well as entropy, is a partition of Ω, i.e., {∆
α ⊂ Ω},
α = 1, … ,
G, with ∪
α∆
α = Ω, ∆
α ∩ ∆
β = ∅ for
α ≠
β. Let
χα be the characteristic function of ∆
α and let
vα =
µ(∆
α) (> 0). If
f is a function on Ω, its coarse graining is defined to be
Let the system’s distribution in Ω be described by a density function
ρ(
ω). The primitive entropy is defined as
and is constant in time. The entropy to be used here is defined as
with
formed from
ρ as in Eq. (1). It is easy to show that
where
![Entropy 07 00221 i004]()
, and the function
S(
p|q) is the
relative entropy defined by
with
p and
q probability distributions such that
q(
x) vanishes only if
p(
x) does. Note that ∑
ρα = ∫
ρ = 1.
The selection of coarse grains is itself a question of great interest and elsewhere [
4] we have argued that this arises from the dynamics, with dependence on the temporal precision of observers. The physical ideas lying behind Ref. [
4] are not new (see Ref. [
5]) but as far as I know had not previously submitted to precise implementation.
2.1 Symmetric behavior of entropy in the two-time boundary condition context
So far everything is time-symmetric. (The transformation
ϕ(t) is also assumed time-symmetric, with a general definition of this symmetry given in Ref. [
6].) To maintain time symmetry one must be careful to set the boundary value problem symmetric as well. As I have often emphasized, the use of initial conditions can slyly enter a problem, leading occasionally to circular “demonstrations” of an arrow of time. For this reason the dynamical problem for this system is formulated by the demand that the system be found in particular coarse grains at separated times, say
ϵ0, at time-0 and
ϵT at time-
T. I focus on thermodynamic behavior between these times [
7]. For symmetry take
µ(
ϵ0) =
µ(
ϵT). The points of Ω satisfying this two-time boundary condition are
To proceed I make the following assumption: the dynamical map,
ϕ(t) is mixing, and there is a time
τ such that for all coarse grains the characteristic decorrelation property holds for
t > τ. Specifically,
for t > τ and for A and B macroscopic (i.e., unions of coarse grains)
The usual mixing condition only demands the above factoring, or decorrelation, for
t → ∞. The equality in Eq. (4) is shorthand for “equal up negligible quantities” which here correspond to numbers much smaller than the measure of any coarse grain. The time-
t image of the set
ϵ is
To calculate the entropy I need
ρα(
t)
For
T −
t > τUsing the measure-preserving property of
ϕ(t), a factor
µ(
ϵT) appears in both numerator and denominator leading to
This is precisely what one gets
without future conditioning, so that all macroscopic quantities, and in particular the entropy, are indistinguishable from their unconditioned values.
Working backward from time-
T one obtains an analogous result. Define
s ≡ T −
t and set
. Then
If
s satisfies
T −
s > τ, then when the density associated with
is calculated its dependence on
ϵ0 drops out. It follows that
For a time-reversal invariant dynamics this gives the entropy the same time dependence coming back from
T as going forward from 0.
The proximity to low entropy boundary conditions thus induces the usual entropically defined thermodynamic arrow, where “proximity” is based on the equilibration time scale,
τ. Physical systems typically have more than a single time scale. In fact, as suggested by Ref. [
4], the definition of coarse grains generally depends on the existence of a scale shorter than
τ, such that on that smaller scale the system relaxes
within the grain.
2.2 Symmetric behavior of causality in the two-time boundary condition context
In the same two-time boundary condition context, a perturbation-based notion of macroscopic causality can also be deduced. Using two-time boundary conditions one considers dynamical evolution with unperturbed and perturbed dynamics. “Perturbed” means that at a specified intermediate time an additional force acts. When solving the perturbed and unperturbed boundary value problems, there will be different microscopic solutions. In principle, the macroscopic solutions could differ at all intermediate times. However, in a system with causality they differ on only one side of the perturbation.
Let the time interval for the boundary value problem be [0,
T]. Call the unperturbed system A; its boundary conditions and history are as described in the previous section. It evolves under
ϕ(t), its boundary conditions are
ϵ0 and
ϵT, and its microstates are
(formerly called
ϵ). System B, the perturbed case, has an additional transformation act at time-
t0. Call this transformation
ψ. It should not be dissipative—I do not want an arrow from such an asymmetry [
8,
9].
ψ is thus invertible and measure preserving and for simplicity is assumed instantaneous. Solutions of the boundary value problem evolve from
ϵ0 to
ϵT under
. The microstates for system B are therefore in
Clearly,
ϵ(A) ≠
ϵ(B). But as I now show, for mixing dynamics and for sufficiently large
T, the following hold: 1) for
t0 close to 0, the only macroscopic difference between A and B are for
t > t0; 2) for
t0 close to
T, the only macroscopic differences are for
t < t0. This means that the direction of causality coincides with the direction of entropy increase.
The proof is nearly the same as above. Again use the time
τ such that the mixing decorrelation holds for time intervals longer than
τ. First consider
t0 close to 0. The observable macroscopic quantities are the densities in grain-∆
α, which are, for
t < t0,
As before, the mixing property, for
T −
t >
τ, yields
![Entropy 07 00221 i017]()
, which is the initial-value-only macroscopic time evolution. For
, the only difference is to add a step,
ψ−1. Unless
ψ−1 is diabolically contrived to undo
ϕ(−u) for large
u, this will not affect the argument that showed that the dependence on
ϵT disappears. Thus A and B have the same macrostates before
t0.
For
t > t0,
continues its behavior as before. For
things are different:
Now I require
T −
t > τ . If this is satisfied the
ϵT dependence drops out and
This shows that the effect of
ψ is the usual initial-conditions-only phenomenon.
If we repeat these arguments for
t such that
T −
t is small, then just as we showed in
Sec. 2.1, the effect of
ψ will only be at times
t less than t0.
2.3 Analysis of a macroscopic system in this context
Either based on the above arguments or on other approaches to the thermodynamic arrow, the computer can be treated as a macroscopic system whose underlying microscopic dynamics is reversible, but which nevertheless, when treated macroscopically can have irreversible aspects. Moreover, it will be treated as an open system, allowing further introduction of irreversible behavior. Suppose that a collection of dynamical variables has been identified for the computer. Then it would be reasonable to use the Langevin equation for the motion. The reversible terms in this equation represent the pure underlying dynamics, while the irreversible term plus the noise arise from suppressed degrees of freedom—the usual justification for that equation. Moreover, the sign of the irreversible term would be the expression of the thermodynamic arrow. Finally, considering the density function for the computer’s degrees of freedom, it should satisfy a high-dimensional Fokker-Plank equation, as is usual for densities of systems obeying a Langevin equation.
2.4 Prediction and retrodiction
In Ref. [
2] I discussed the equivalence of the arrow of time to the fundamental distinction between prediction and retrodiction for macroscopic states. For prediction one takes equal probability for all microstates consistent with the given macrostate and averages over their subsequent motion. For retrodiction one makes guesses about the earlier microstates and accepts those that arrive in the required macrostate. The guesses are also informed by other considerations so that one is effectively using Bayesian statistics.
It is paradoxical that by this method of knowing the future may be more certain than the past. Take a glass of water with a small piece of ice at 2 p.m. Suppose it to be isolated from 1 p.m. to 2 p.m. and from 2 p.m. to 3 p.m. The 3 p.m. state is not in doubt: a colder glass of water. But what is the 1 p.m. precursor? Two pieces of ice, one of them small? One big cube? One big sphere? There is no way to know.
But the paradox is only that: when we—or a computer—“knows” the past we do not attain this knowledge by retrodicting (but see
Sec. 4). If someone is an eyewitness (seeing an ice
cube, say) that observation is transmitted and stored in the brain. Without worrying about the exact storage mechanism, what has been done is the creation of a
record of the past. The states maintaining this record have the property that they do not change—if memory is good—so for them the retrodiction problem is trivial. (This property can also be stated as the possession of few predecessors [
2].) It is this record that is the past. Indeed we distinguish between “knowing” the past in this way and “knowing” it by retrodictive calculation: “I saw it was a cube of 2 cm,” versus “I suppose it was a 2 cm cube because the local source of ice is a freezer that only makes cubes and it would have had to be about 2 cm to reach the present size in this environment.” (Note too the Bayes-like use of outside information.)
3 A computer
However abstract this discussion may become, the computer is to be thought of as a physical system, like a steam engine or a cuckoo clock. It is attached to a power source, usually thought of as supplying energy, but more significantly characterized as a source of negentropy. (The total energy in the machine is secondary; in fact effort must be expended to keep it cool. Similar energy balance issues exist for the planet: the role of the computer power supply thus resembles the role of the sun vis a vis the earth.)
Each bit of data or program is held in a “two-state” physical subsystem. Ideally this is pictured as a double-well potential with a high barrier. Actual computers have far more internal degrees of freedom for each bit; so many, that for example one can generally assign a temperature to the storage unit. The characteristic features though are the high barrier when the system is left alone and the existence of a mechanism that easily moves the bit from one “state” (which is really a collection of microstates) to another. The high barrier, preventing spontaneous transitions, insures the reliability of retrodiction. Call the state and system,
ω ∈ Ω. The function of the CPU is to move the system from one point to another within Ω. For humans the states are more subtle with actual storage mechanisms far from understood [
10,
11,
12,
13,
14,
15,
16].
There is also a clock. Although asynchronous computers exist, most machines march to a definite beat. For humans there is no overall synchronization, although locally (as in pacemakers) it can be crucial. I mention this because in the context of psychological arrows there is often discussion of the meaning of the “present.” For the computer I do not believe the ticks of its clock define the duration of “present,” so that one not be concerned with the presence or absence of mental synchronous processing. Rather I expect the computer’s present to be the interval between writes to the record file as will be described below.
Computations are accompanied by dissipation, so much so that one of the principal issues for Intel’s Itanium chip is its power consumption [
17]. More fundamentally, Landauer [
18,
19] has shown that computation requires irreversible processes and heat generation. From the standpoint of our two-state systems (where those “two” states are
macrostates), the system will typically enter a new macrostate in a microstate with relatively high energy. Dropping to a lower energy of the same macrostate produces heat energy and allows the system to “forget” its recent arrival and be indistinguishable from a system that had been in this state indefinitely. This represents a loss of information.
There is also an evolutionary process that applies to computers. It is not Darwinian survival of the best software and hardware, as is evident to anyone who has had an effective tool made obsolete by the ongoing march of commercial interests. Nevertheless, consumers do have a vote, and what pleases them and fulfills their needs tends to survive.
Both computers and animals find it convenient to have (at least) two kinds of memory, long term and short term. In view of the difficulty of finding a full physiological basis for any memory in the brain, one does not expect there to be much resemblance in the physical mechanisms of the two systems. Nevertheless, the usefulness of maintaining both sorts of memory appears to be common. One might also construe the overall architecture of humans or machines to be a kind of memory, in the sense that a good deal of the underlying programming of both machines and people is built into the structures of the respective entities. Thus the genome is a kind of memory as is the wiring diagram, evolved and extended from earlier versions, of a chip.
4 Arrow-like features in computer states
I consider a computer whose job it is to record, predict (and perhaps influence as explained below) the weather. It is an open system and interacts with the external world in three principal ways: (1) acquisition of needed resources (electricity, air for cooling, etc.), (2) input via “sensory” channels (keyboard, mouse, updates on current weather, both through links to raw data and through connections to other computers that get and process similar data) and (3) output to monitor, disks, links to other machines. It was created, hooked up and turned on by a human at some time in the past. “Past” here is in accordance with the thermodynamic arrow, which is given. The operation of the computer is that of a physical device (transistors, motors, cables, etc.) in the context of this thermodynamic arrow. The objective is to see how many properties of the consciousness or psychological arrow may be attributed to the computer, given this thermodynamic arrow.
I assume that the programming of the machine is such that at any given moment the weather information in the computer is of several kinds:
In long term memory: records of actual weather patterns (including collected data).
In long term memory: records of weather patterns computed by the machine, for times at which the machine also has actual weather patterns (Item 1).
In long term memory: records of weather patterns computed by the machine for times at which the machine does not have actual weather patterns. These can be both for times before and after the current external present.
In short term memory: records of weather patterns that are already computed but not yet stored in long term memory. (Relation to external time as in Item 3.) Also external weather patterns currently being input.
In short term memory: temporarily stored numbers involved in computing the next weather pattern.
In addition a considerable portion of the machine memory may hold computer programs, which themselves span a hierarchy of types: programs written for this task, software that implements these programs (e.g., codes for Fortran), low level utility programs as well as the operating system. The physical device takes the machine from one “state” to another, where “state” is a list of all bits in the foregoing inventory.
For a well-written program the way the machine handles these different kinds of information parallels the way we do. The past will include all patterns in Item 1. A separate part of the past will be the memory in Items 2 and 3. The computer will distinguish these as its own “opinions,” its guesses, some of which have been checked against authority (Item 1). If the computer needs to check the information in Item 4 (perhaps while moving forward with the next calculation), this too will be considered past.
What then is future? In practice this is what the machine
will compute or will receive from external links. But in the machine itself there isn’t any. It is prepared to accept new data to add to Items 1, 2 and 4, and to this extent shows awareness that there
is a future. Moreover, provisions for the future can go beyond the programming necessary for the computer to be ready to accept new data. There can also be an ability to act, to influence the future. For example, in response to inadequate data it may automatically launch a weather balloon, or inform a human of the need to do so. It might even institute cloud seeding operations in an attempt to increase rainfall (presumably having been programmed to do this and linked to appropriate external devices). What I call “awareness” of the future is thus the fact that built into the program is the ability to accept new data, continue the computation while receiving new data or transferring data between short and long term memory, as well as provisions in the program to respond to certain states by issuing particular kinds of output, such as seeding a cloud. This is not different from our relation to the future, except that our “programming” developed through a process of biological evolution (which certain computer programs emulate [
20]).
And the concept of “present”? Comparison with our own experiences suggests that the interval between writing calculated patterns to short term memory is the appropriate analogue. If the machine multitasks by accepting external weather input simultaneously with its calculations, the human analogy is less clear although we too are fitted for multitasking: most of us
can chew gum and walk at the same time [
21].
The distinctions above regarding past, present and future apply to what I called a well-written program. This recalls the existence of humans who do not possess a “normal” sense of time. Saniga [
22,
23,
24,
25] has collected many examples of this from the literature of psychopathology and interpreted these unusual perspectives in terms of projective spaces.
For a computer, as for a person, a check of memory is technically speaking a retrodiction. (This check may be part of its continuing program, perhaps to improve performance by looking for sources of error in previous work, or it may be introspection due to encountering unanticipatable events, such as a query from a human using the machine.) When pulling up “old” records it equates the stored 0s and 1s in its memory as a weather pattern, effectively retrodicting by “believing” those bits to be the same as it earlier wrote. Here is where my earlier remarks on the characteristics of good memory registers plays a role. They should be states with few precursors, in fact one precursor, the same state. Here too “state” should be interpreted as a coarse grain in which (e.g.) only the magnetic configuration is relevant, temperature and small variations in magnetization being ignored. For these systems retrodicting is reliable.
There is also poor memory. Files may be corrupted (including by viruses) and the computer may or may not be aware of this, where “aware” means the bad data are flagged, perhaps having failed some check-digit test. A computer may also have false or implanted memories, the skullduggery being different from that in the human phenomenon, but the result analogous.
5 Conclusions
The computer has a past that is in many ways as rich as our own, complete with memories of actual events, of its impressions of those events, of its calculated predictions for future events. For the example given above, it also maintains an image of the world. Further, it has a present delineated by intervals between the creation of new memories, probably a bit more well defined than our own present. It is prepared for the future and may act to affect that future. It does all this without an independent arrow of time, retaining the past/future distinction by virtue of its being part of a mechanistic world with a thermodynamic arrow in a particular direction. For the computer, as for us, the past is over, complete. In a well-written program, files in the enumerated categories of
Sec. 4 are not tampered with. Similarly, the future is open, in the sense that it is nowhere contained in a memory file. It has an existence in that the machine is programmed to deal with certain kinds of input (“contingencies”) as well as the results of its own calculations.
The point of this article is that in view of all this parallel structure there is no reason to postulate an independent psychological arrow. This is a reductionist view that may not be acceptable to some.
I close with a disclaimer. It is assumed throughout this article that the Second Law of Thermodynamics is an objective statement about the world, like Einstein’s General Relativity, whereas the psychological arrow is lacking in full definition because of its subjective nature. But the Second Law has subjective elements as well. At its core is an essential distinction between the microscopic and the macroscopic, equivalent to the distinction between work and heat, equivalent in turn to the selection of coarse grains in phase space or Hilbert space. The choice of coarse grains has important aspects of subjectivity, so that the superior position of the Second Law vis a vis the definition of a psychological arrow may be questioned. Recent work [
4] has addressed this question in a precise way and implementation of the physical idea that coarse grains correspond to objectively slow variables has begun. My belief in the ultimate success of this program leads me back to the conclusion that the psychological arrow is the dependent concept, but one should not be too dogmatic.
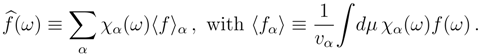
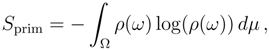
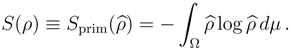
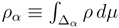 , and the function S(p|q) is the relative entropy defined by
, and the function S(p|q) is the relative entropy defined by

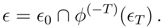

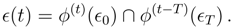
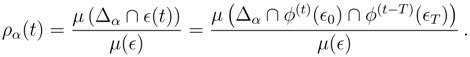
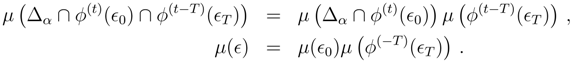
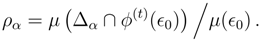
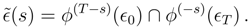
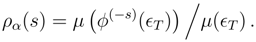
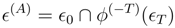
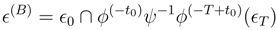
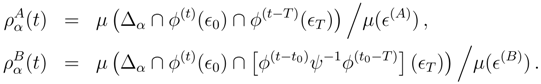
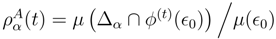 , which is the initial-value-only macroscopic time evolution. For , the only difference is to add a step, ψ−1. Unless ψ−1 is diabolically contrived to undo ϕ(−u) for large u, this will not affect the argument that showed that the dependence on ϵT disappears. Thus A and B have the same macrostates before t0.
, which is the initial-value-only macroscopic time evolution. For , the only difference is to add a step, ψ−1. Unless ψ−1 is diabolically contrived to undo ϕ(−u) for large u, this will not affect the argument that showed that the dependence on ϵT disappears. Thus A and B have the same macrostates before t0.