Construction of a Robust Cofactor Self-Sufficient Bienzyme Biocatalytic System for Dye Decolorization and its Mathematical Modeling
Abstract
:1. Introduction
2. Results and Discussion
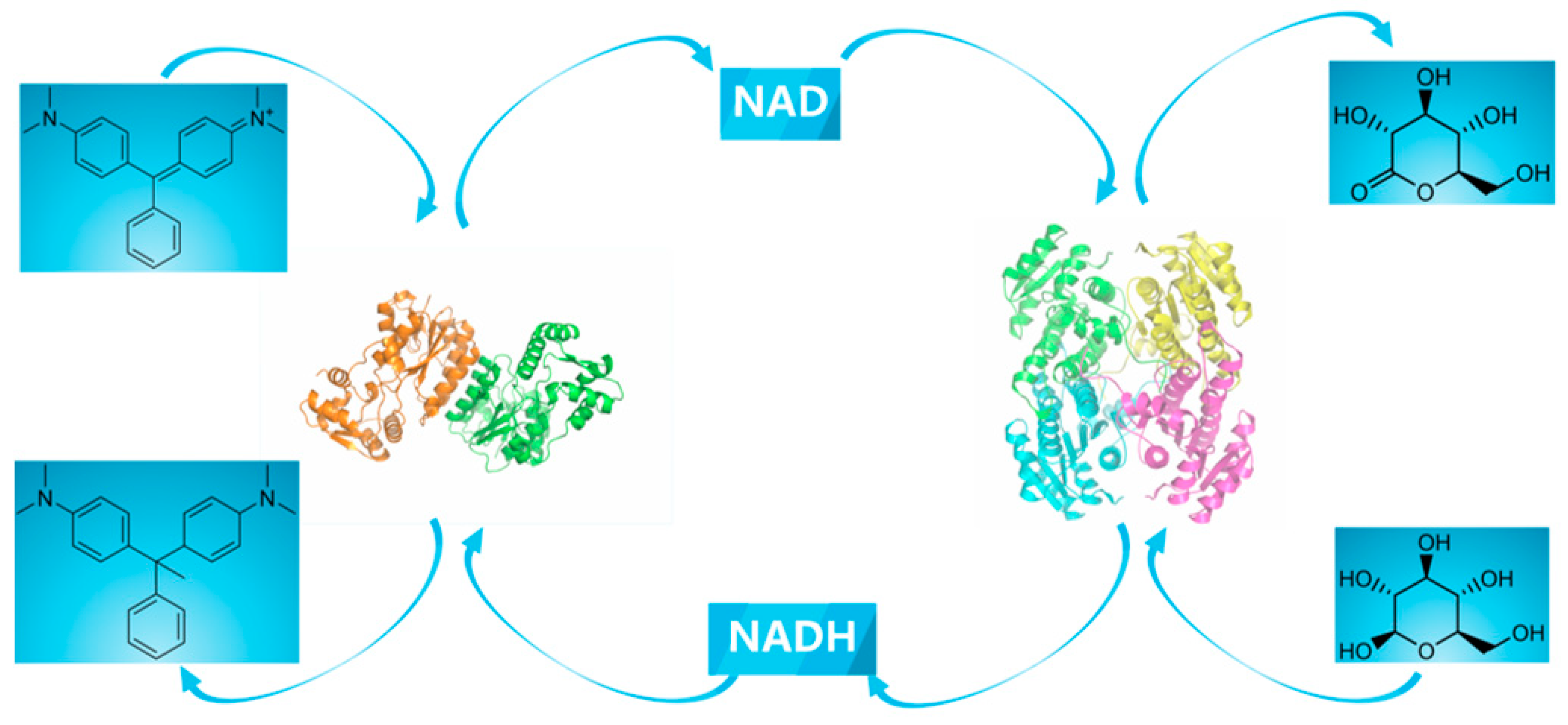
2.1. Construction of a Self-Sufficient Bienzyme Biocatalytic System for Dye Decolorization
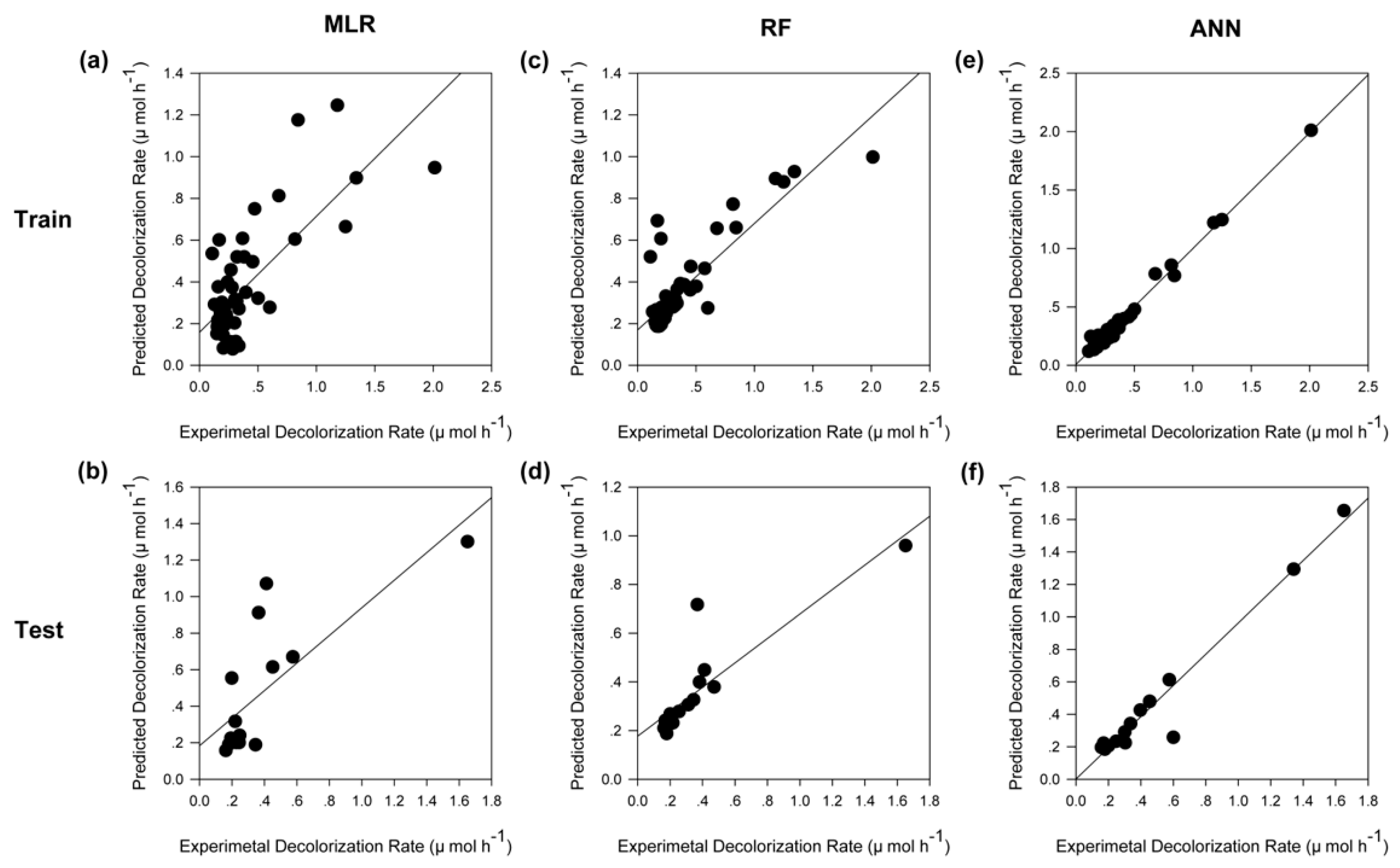
2.2. Modeling by Multiple Linear Regression
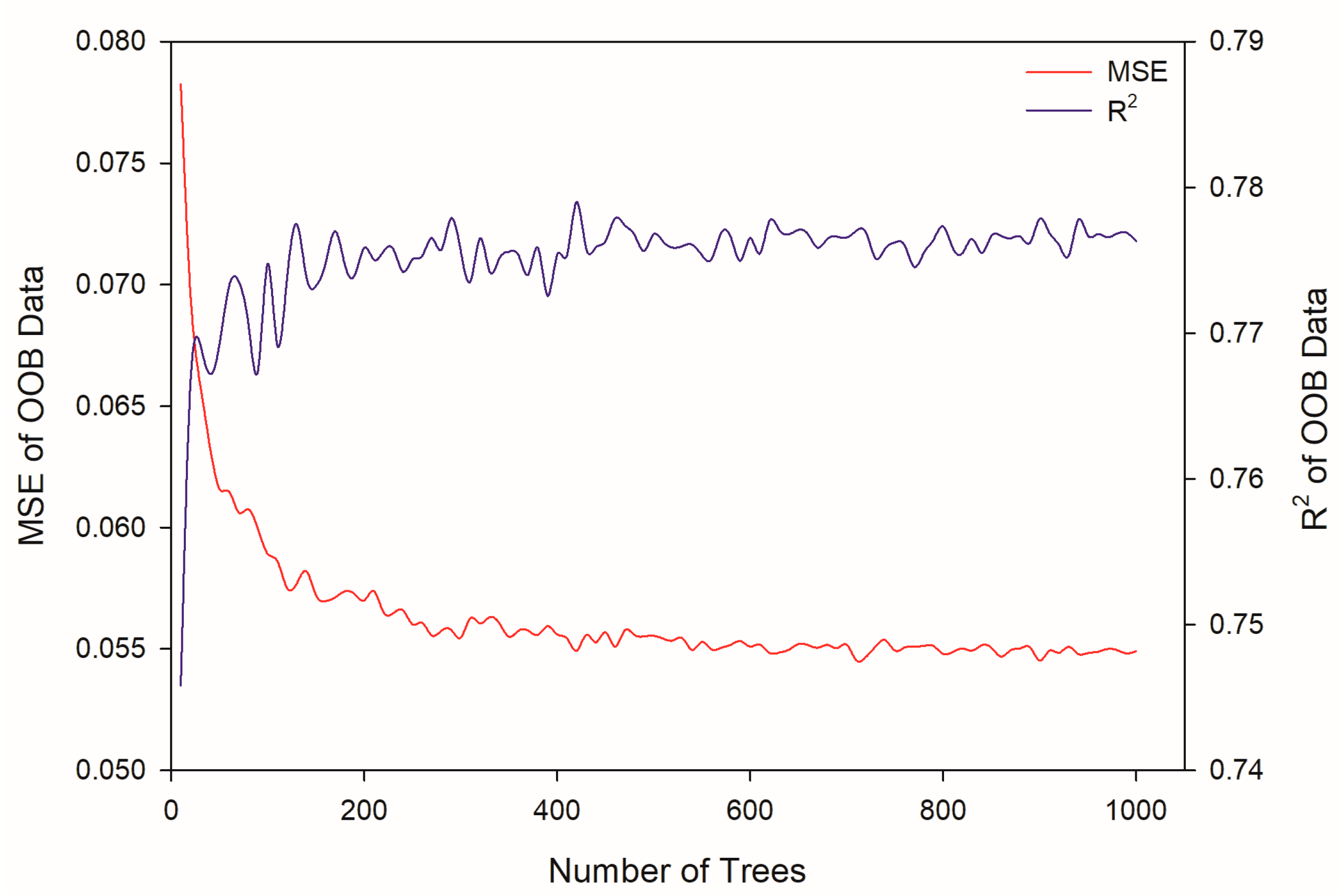
2.3. Modeling by Random Forest
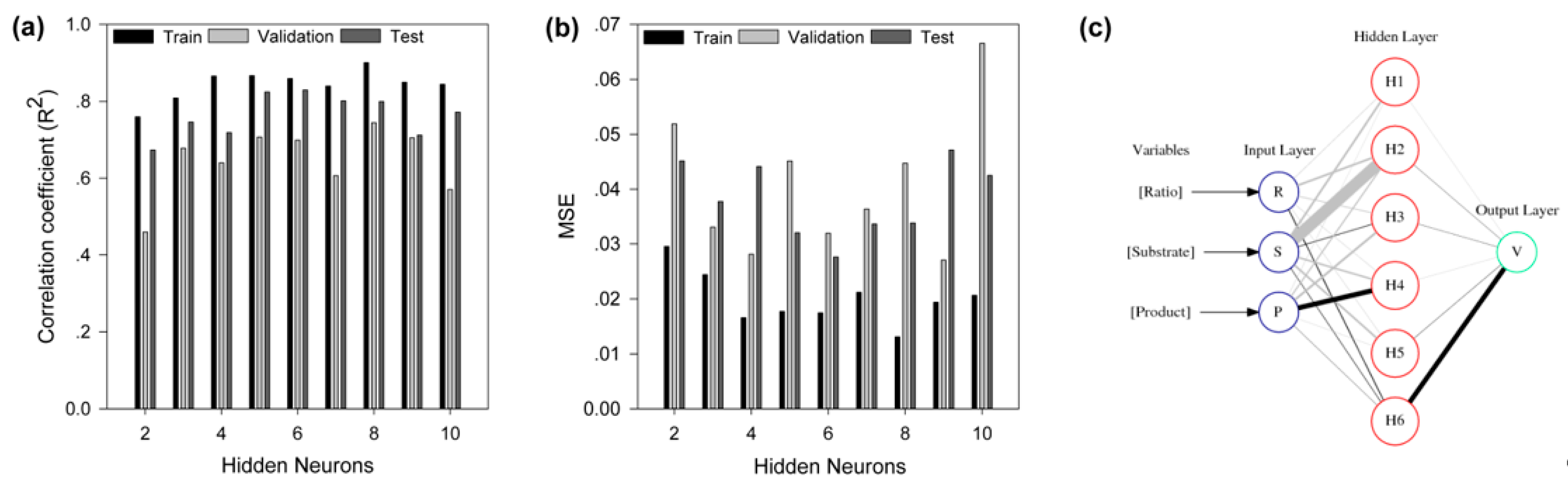
2.4. Modeling by Artificial Neural Network
2.5. Model Comparision
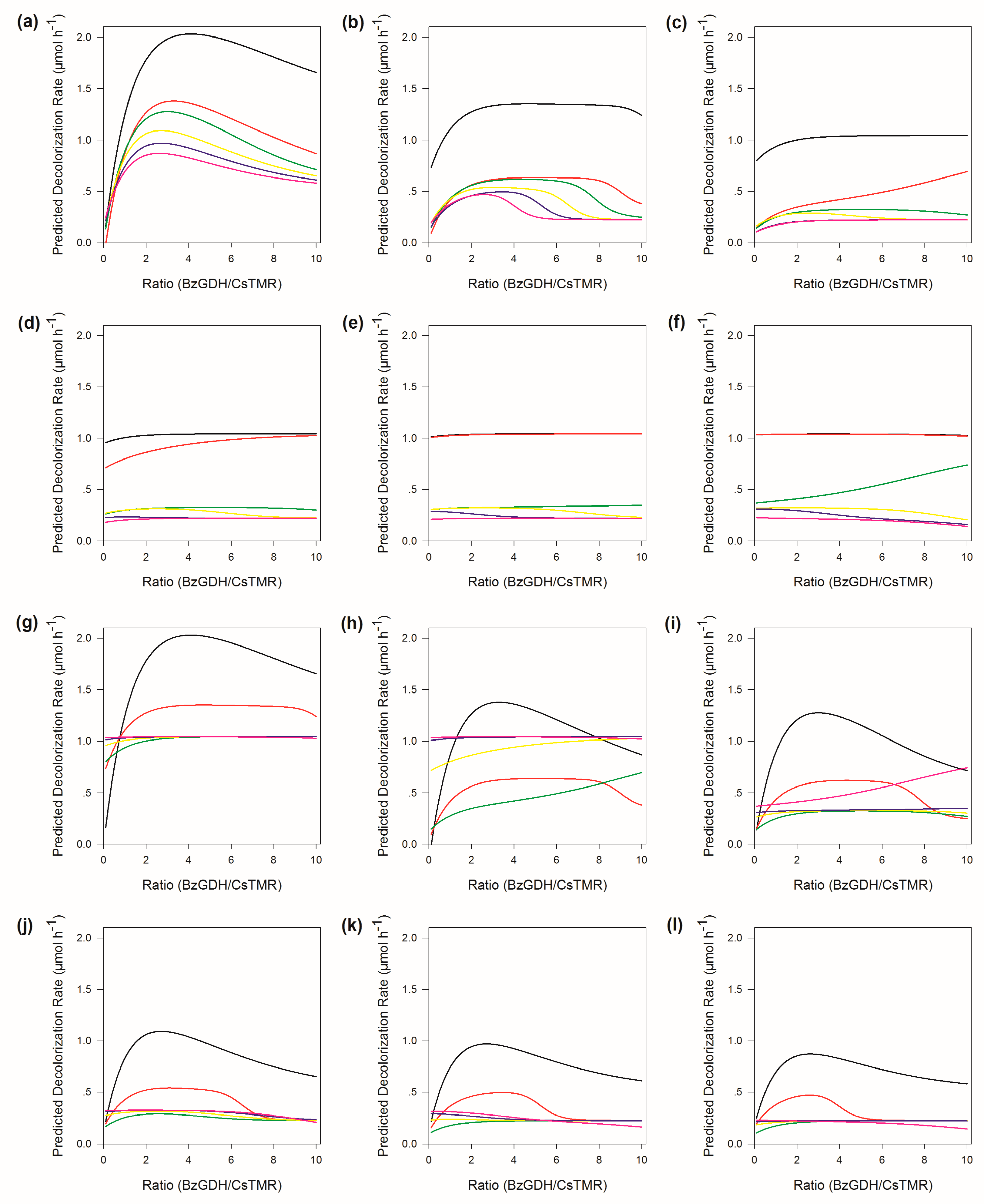
2.6. Weights Analysis of ANN
2.7. Sensitivity Analysis of ANN
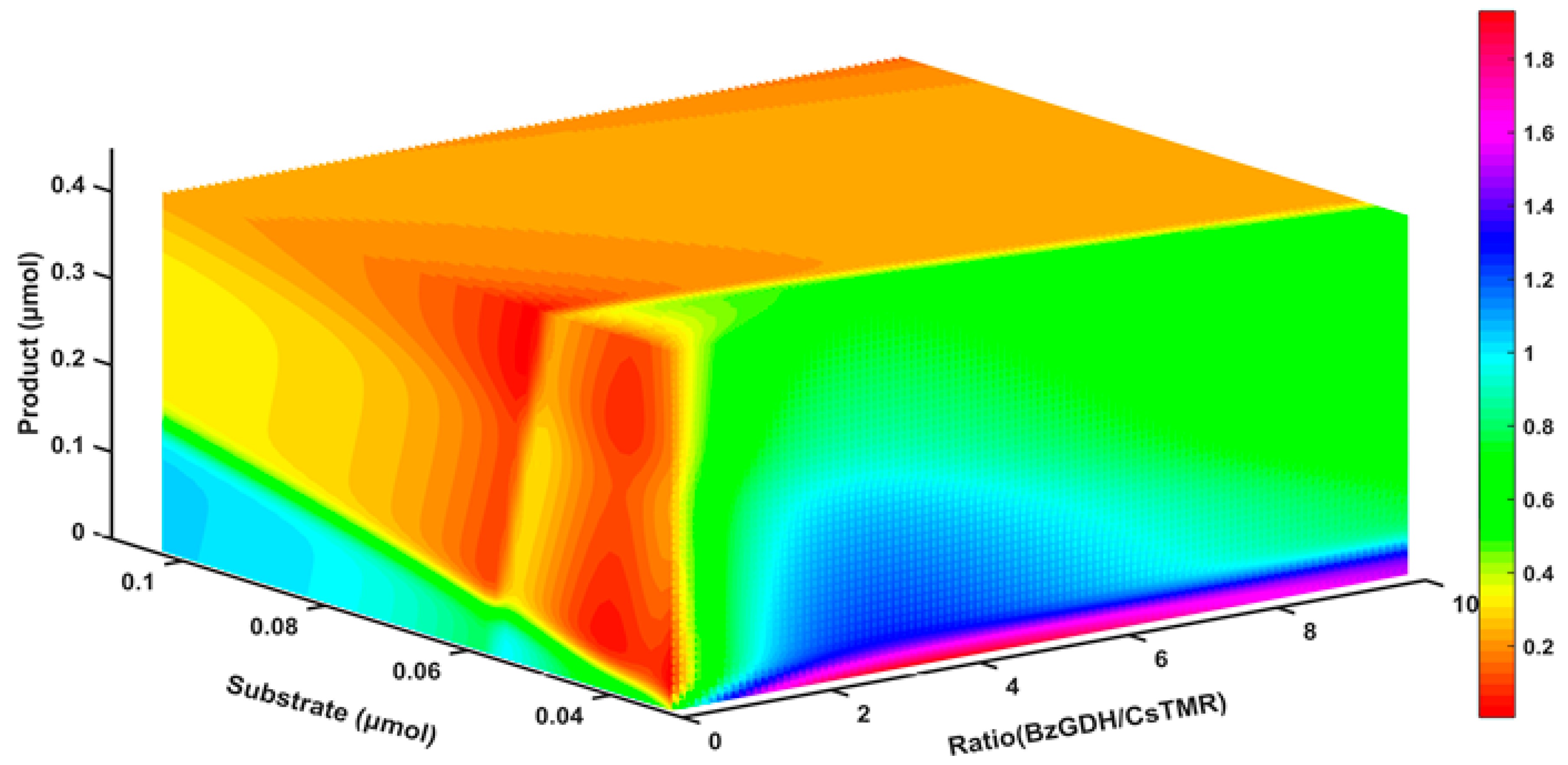
2.8. The Response of the Decolorization Efficiency to Other Variables
3. Materials and Methods
3.1. Strains, Plasmids, and Chemicals
3.2. Preparation of Recombinant Enzymes
3.3. Enzyme Activity Assays
3.4. Construction of a Cofactor Self-Sufficient Bienzyme Biocatalytic System for Dye Decolorization
3.5. Modeling by Multiple Linear Regression
3.6. Modeling by Random Forest
3.7. Modeling by Artificial Neural Network
3.8. Model Comparision
3.9. Neural Interpretation Diagram
3.10. Estimation of the Importance of Variables
3.11. Sensitivity Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gregory, P. Dyes and Dye Intermediates; Wiley: New York, NY, USA, 1993; pp. 544–545. [Google Scholar]
- Boulos, R.A. Antimicrobial dyes and mechanosensitive channels. Antonie. Van. Leeuwenhoek 2013, 104, 155–167. [Google Scholar] [CrossRef]
- Weisburger, J.H. Comments on the history and importance of aromatic and heterocyclic amines in public health. Mutation Res. 2002, 506–507, 9–20. [Google Scholar] [CrossRef]
- Vršanská, M.; Voběrková, S.; Jiménez Jiménez, A.M.; Strmiska, V.; Adam, V. Preparation and Optimisation of Cross-Linked Enzyme Aggregates Using Native Isolate White Rot Fungi Trametes versicolor and Fomes fomentarius for the Decolourisation of Synthetic Dyes. Inter. J. Env. Res. Pub. Heal. 2018, 15, 23. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, J.; Leng, J.; Yang, X.; Liao, L.; Liu, L.; Xiao, A. Enhanced Performance of Magnetic Graphene Oxide-Immobilized Laccase and Its Application for the Decolorization of Dyes. Molecules 2017, 22, 221. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zimbardi, A.; Camargo, P.F.; Carli, S.; Aquino Neto, S.; Meleiro, L.P.; Rosa, J.C.; De Andrade, A.R.; Jorge, J.A.; Furriel, R.P.M. A High Redox Potential Laccase from Pycnoporus sanguineus RP15: Potential Application for Dye Decolorization. Int. J. Mol. Sci. 2016, 17, 672. [Google Scholar] [CrossRef] [Green Version]
- Jang, M.S.; Lee, Y.M.; Kim, C.H.; Lee, J.H.; Kang, D.W.; Kim, S.J.; Lee, Y.C. Triphenylmethane reductase from Citrobacter sp. strain KCTC 18061P: purification, characterization, gene cloning, and overexpression of a functional protein in Escherichia coli. Appl. Environ. Microbiol. 2005, 71, 7955–7960. [Google Scholar] [CrossRef] [Green Version]
- Hummel, W. Large-scale applications of NAD(P)-dependent oxidoreductases: recent developments. Trends Biotechnol. 1999, 17, 487–492. [Google Scholar] [CrossRef]
- Liu, W.; Wang, P. Cofactor regeneration for sustainable enzymatic biosynthesis. Biotechnol. Adv. 2007, 25, 369–384. [Google Scholar] [CrossRef]
- Liu, Z.Q.; Ye, J.J.; Shen, Z.Y.; Hong, H.B.; Yan, J.B.; Lin, Y.; Chen, Z.X.; Zheng, Y.G.; Shen, Y.C. Upscale production of ethyl (S)-4-chloro-3-hydroxybutanoate by using carbonyl reductase coupled with glucose dehydrogenase in aqueous-organic solvent system. Appl. Microbiol. Biotechnol. 2015, 99, 2119–2129. [Google Scholar] [CrossRef]
- Siriphongphaew, A.; Pisnupong, P.; Wongkongkatep, J.; Inprakhon, P.; Vangnai, A.S.; Honda, K.; Ohtake, H.; Kato, J.; Ogawa, J.; Shimizu, S.; et al. Development of a whole-cell biocatalyst co-expressing P450 monooxygenase and glucose dehydrogenase for synthesis of epoxyhexane. Appl. Microbiol. Biotechnol. 2012, 95, 357–367. [Google Scholar] [CrossRef]
- Zhang, Y.; Arugula, M.A.; Wales, M.; Wild, J.; Simonian, A.L. A novel layer-by-layer assembled multi-enzyme/CNT biosensor for discriminative detection between organophosphorus and non-organophosphrus pesticides. Biosens. Bioelectron. 2015, 67, 287–295. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Gao, F.; Zhang, S.P.; Su, Z.G.; Ma, G.H.; Wang, P. Simultaneous production of 1,3-dihydroxyacetone and xylitol from glycerol and xylose using a nanoparticle-supported multi-enzyme system with in situ cofactor regeneration. Bioresour. Technol. 2011, 102, 1837–1843. [Google Scholar] [CrossRef] [PubMed]
- Bhaskar, U.; Li, G.; Fu, L.; Onishi, A.; Suflita, M.; Dordick, J.S.; Linhardt, R.J. Combinatorial one-pot chemoenzymatic synthesis of heparin. Carbohydr. Polym. 2015, 122, 399–407. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Basheer, I.A.; Hajmeer, M. Artificial neural networks: fundamentals, computing, design, and application. J. Microbiol. Methods 2000, 43, 3–31. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Boulesteix, A.-L.; Janitza, S.; Kruppa, J.; König, I.R. Overview of random forest methodology and practical guidance with emphasis on computational biology and bioinformatics. Wires. Data Min. Knowl. 2012, 2, 493–507. [Google Scholar] [CrossRef] [Green Version]
- Ding, H.; Gao, F.; Yu, Y.; Chen, B. Biochemical and Computational Insights on a Novel Acid-Resistant and Thermal-Stable Glucose 1-Dehydrogenase. Int. J. Mol. Sci. 2017, 18, 1198. [Google Scholar] [CrossRef] [Green Version]
- Garson, D.G. Interpreting neural network connection weights. Arti. Intell. Expert 1991, 6, 46–51. [Google Scholar]
- Aleboyeh, A.; Kasiri, M.; Olya, M.; Aleboyeh, H. Prediction of azo dye decolorization by UV/H2O2 using artificial neural networks. Dyes. Pigments. 2008, 77, 288–294. [Google Scholar] [CrossRef]
- Olden, J.D.; Joy, M.K.; Death, R.G. An accurate comparison of methods for quantifying variable importance in artificial neural networks using simulated data. Ecol. Model 2004, 178, 389–397. [Google Scholar] [CrossRef]
- Olden, J.D.; Jackson, D.A. Illuminating the “black box”: a randomization approach for understanding variable contributions in artificial neural networks. Ecol. Model 2002, 154, 135–150. [Google Scholar] [CrossRef]
- Lek, S.; Delacoste, M.; Baran, P.; Dimopoulos, I.; Lauga, J.; Aulagnier, S. Application of neural networks to modelling nonlinear relationships in ecology. Ecol. Model 1996, 90, 39–52. [Google Scholar] [CrossRef]
- Efron, B. Bootstrap Methods: Another Look at the Jackknife. In Breakthroughs in Statistics: Methodology and Distribution; Kotz, S., Johnson, N.L., Eds.; Springer New York: New York, NY, USA, 1992; pp. 569–593. [Google Scholar]
- Wolpert, D.H.; Macready, W.G. An Efficient Method To Estimate Bagging’s Generalization Error. Mach. Learn 1999, 35, 41–55. [Google Scholar] [CrossRef] [Green Version]
- Özesmi, S.L.; Özesmi, U. An artificial neural network approach to spatial habitat modelling with interspecific interaction. Ecol. Model 1999, 116, 15–31. [Google Scholar] [CrossRef]
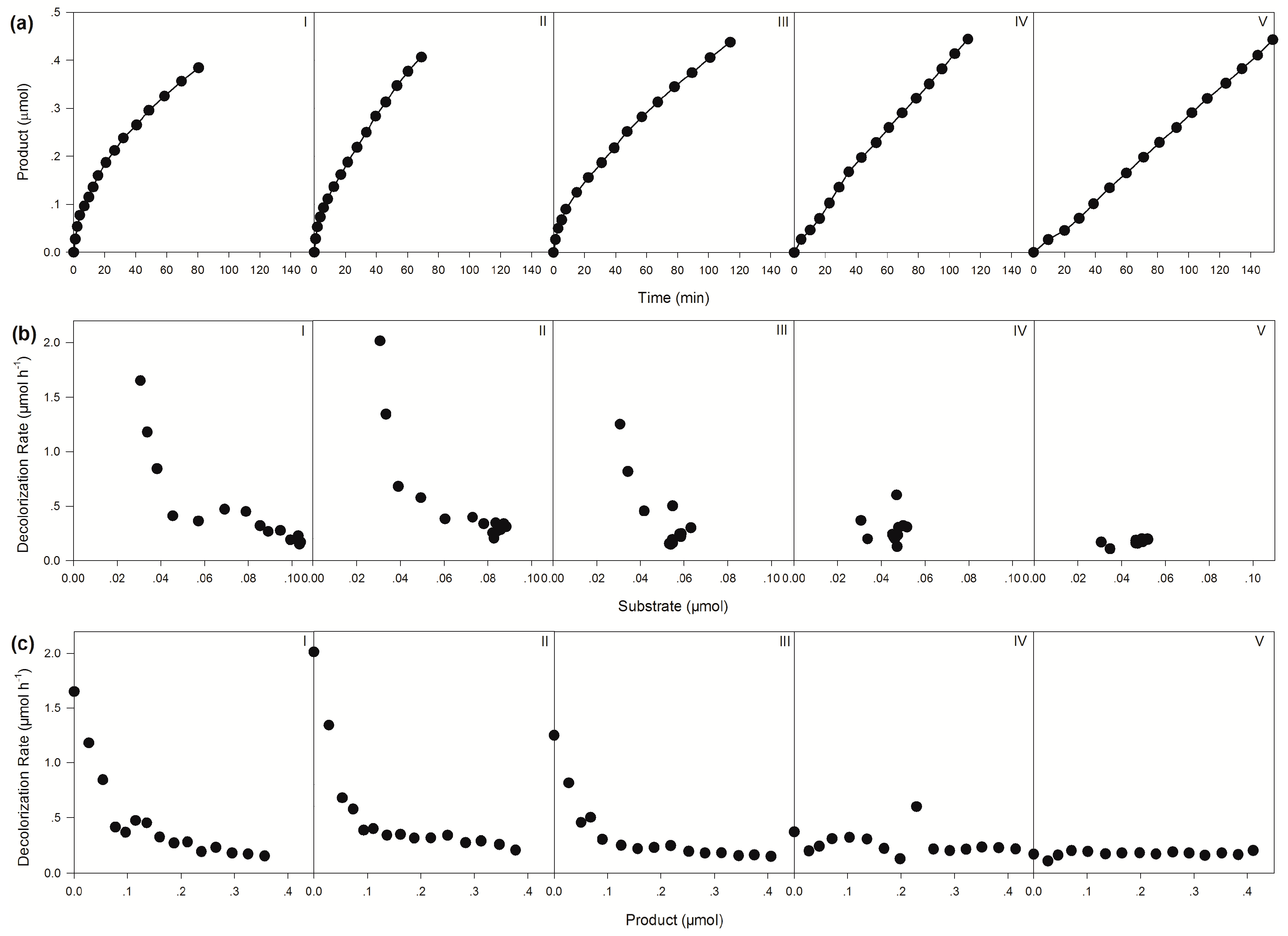
| Apparent Decolorization Rates (μmol h−1) | |||||
|---|---|---|---|---|---|
| Molar ratio of CsTMR/BzGDH | |||||
| 1:10 | 1:5 | 1:1 | 5:1 | 10:1 | |
| Initial | 1.65 | 2.01 | 1.25 | 0.37 | 0.17 |
| Average | 0.28 | 0.35 | 0.23 | 0.23 | 0.17 |
| Parameters | MLR | RF | ANN | |||
|---|---|---|---|---|---|---|
| Train | Test | Train | Test | Train | Test | |
| MSE | 0.0511 | 0.0706 | 0.0383 | 0.0419 | 0.0013 | 0.0090 |
| MAE | 0.1474 | 0.1708 | 0.0974 | 0.1031 | 0.0270 | 0.0487 |
| MRE | 48.7130 | 47.7690 | 32.9363 | 24.0703 | 11.1586 | 13.2349 |
| R2 | 0.5552 | 0.5725 | 0.7377 | 0.7602 | 0.9867 | 0.9527 |
| Wi | Wo | |||||
|---|---|---|---|---|---|---|
| Neuron | Variable | Bias | Neuron | Weight | ||
| Ratio | Substrate | Product | ||||
| 1 | −1.0584 | −5.3016 | −0.5183 | 6.9997 | 1 | 0.0944 |
| 2 | −5.3136 | −32.2206 | −3.3973 | −17.0822 | 2 | 0.1495 |
| 3 | −2.0184 | 1.6110 | −5.7296 | 1.1000 | 3 | 0.0555 |
| 4 | −0.7781 | −4.5670 | 13.1172 | 7.7110 | 4 | −0.3755 |
| 5 | −0.7376 | −5.0937 | −0.4546 | −5.3149 | 5 | 0.6968 |
| 6 | 2.2761 | 1.3407 | 0.1931 | 5.0204 | 6 | 12.8454 |
| Bias | −12.5429 | |||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, H.; Luo, W.; Yu, Y.; Chen, B. Construction of a Robust Cofactor Self-Sufficient Bienzyme Biocatalytic System for Dye Decolorization and its Mathematical Modeling. Int. J. Mol. Sci. 2019, 20, 6104. https://0-doi-org.brum.beds.ac.uk/10.3390/ijms20236104
Ding H, Luo W, Yu Y, Chen B. Construction of a Robust Cofactor Self-Sufficient Bienzyme Biocatalytic System for Dye Decolorization and its Mathematical Modeling. International Journal of Molecular Sciences. 2019; 20(23):6104. https://0-doi-org.brum.beds.ac.uk/10.3390/ijms20236104
Chicago/Turabian StyleDing, Haitao, Wei Luo, Yong Yu, and Bo Chen. 2019. "Construction of a Robust Cofactor Self-Sufficient Bienzyme Biocatalytic System for Dye Decolorization and its Mathematical Modeling" International Journal of Molecular Sciences 20, no. 23: 6104. https://0-doi-org.brum.beds.ac.uk/10.3390/ijms20236104





