Thermodynamics and Kinetics of Glycolytic Reactions. Part II: Influence of Cytosolic Conditions on Thermodynamic State Variables and Kinetic Parameters
Abstract
:1. Introduction
2. Results
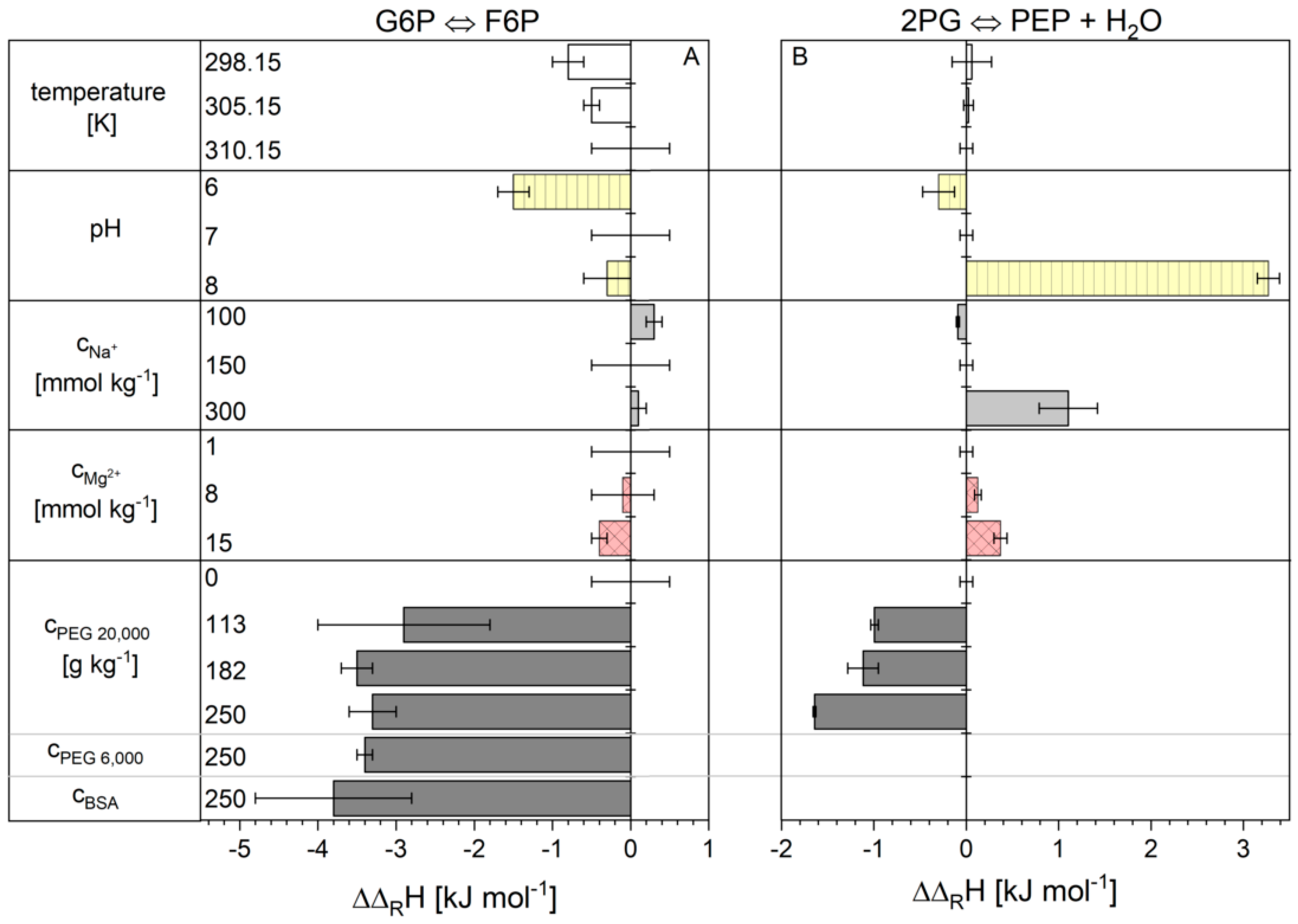
2.1. Influence of the Cytosolic Conditions on the Reaction Enthalpy Change
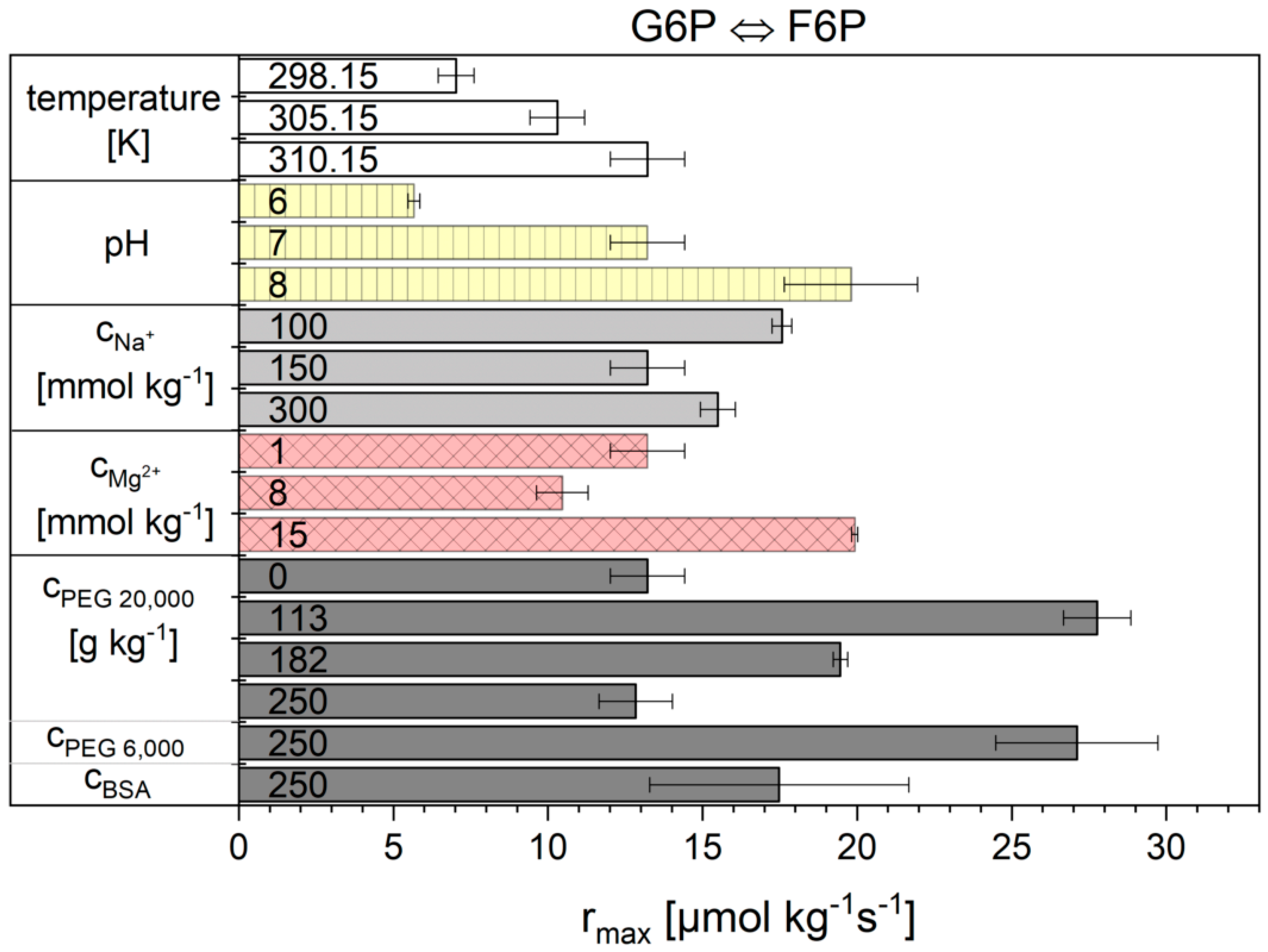
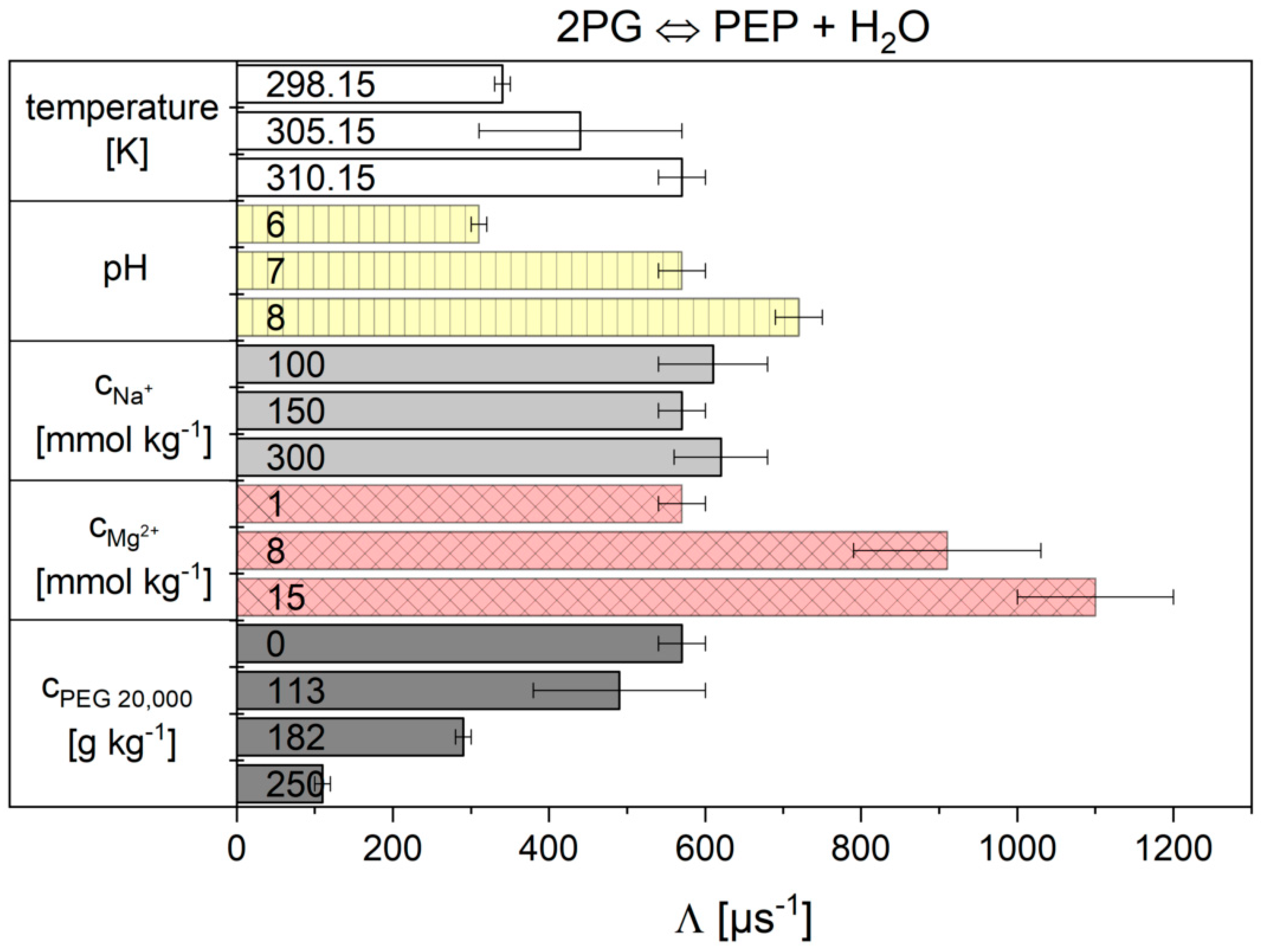
2.2. Influence of the Cytosolic Conditions on the Reaction Kinetics
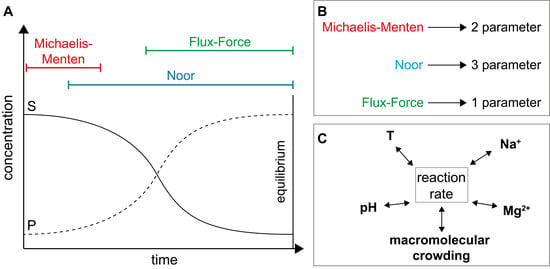
2.2.1. The Noor Model
2.2.2. The Flux-Force Model
3. Discussion
3.1. Influence of the Cytosolic Conditions on the Reaction Enthalpy Change
3.2. Influence of the Cytosolic Conditions on the Reaction Kinetics
3.2.1. Validation of Kinetic Models
3.2.2. Importance of Cytosolic Conditions
3.2.3. Influence on Reaction 2
3.2.4. Influence on Reaction 9
4. Materials and Methods
4.1. Chemicals
4.2. Sample Preparation
4.3. ITC Measurements of the Phosphoglucose Isomerase Reaction
4.4. ITC Measurements of the Enolase Reaction
4.5. Thermodynamic Calculations
4.6. Kinetic Evaluation
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| PEG | polyethylene glycol |
| BSA | bovine serum albumin |
| ITC | isothermal titration calorimetry |
| M-M | Michaelis-Menten |
| G6P | glucose-6-phosphate |
| F6P | fructose-6-phosphate |
| 2PG | 2-phosphoglycerate |
| PEP | phosphoenolpyruvate |
| PGI | phosphoglucose isomerase |
Symbols
| Symbol | Property | Unit |
| r | reaction rate | mol kg−1 s−1 |
| substrate concentration | mol kg−1 | |
| product concentration | mol kg−1 | |
| L | phenomenological coefficient/kinetic parameter | s−1 |
| thermodynamic driving force | - | |
| Gibbs free energy change of biochemical reaction | J mol−1 | |
| standard Gibbs free energy change of biochemical reaction | J mol−1 | |
| universal gas constant (8.314 J∙mol−1∙K−1) | J mol−1 K−1 | |
| temperature | K | |
| activity of component | - | |
| concentration of component | mol kg−1 | |
| kinetic constant of reaction | s−1 | |
| Michaelis constant for substrate/product | mol kg−1 | |
| concentration of component at time 0 | mol kg−1 | |
| equilibrium concentration of component | mol kg−1 | |
| maximum reaction rate | mol kg−1 s−1 | |
| Λ | kinetic parameter | s−1 |
| Q | heat | J |
| reaction enthalpy change of biochemical reaction | J mol−1 | |
| standard entropy change of biochemical reaction | J mol−1 K−1 | |
| P | heat production rate | W |
| m | mass | kg |
| equilibrium-molality ratio of biochemical reaction | -/mol kg−1 | |
| thermodynamic equilibrium constant of biochemical reaction | - | |
| activity-coefficient ratio of biochemical reaction | -/mol kg−1 | |
| rational activity coefficient of component on molality base | - | |
| relative dielectric constant | - |
References
- Hoffmann, P.; Held, C.; Maskow, T.; Sadowski, G. A thermodynamic investigation of the glucose-6-phosphate isomerization. Biophys. Chem. 2014, 195, 22–31. [Google Scholar] [CrossRef] [PubMed]
- Greinert, T.; Vogel, K.; Mühlenweg, J.-K.; Sadowski, G.; Maskow, T.; Held, C. Standard Gibbs energy of metabolic reactions: VI. Glyceraldehyde 3-phosphate dehydrogenase reaction. Fluid Phase Equilibria 2020, 517, 112597. [Google Scholar] [CrossRef]
- Olsen, S.N. Applications of isothermal titration calorimetry to measure enzyme kinetics and activity in complex solutions. Thermochim. Acta 2006, 448, 12–18. [Google Scholar] [CrossRef]
- Tewari, Y.B.; Steckler, D.K.; Goldberg, R.N. Thermodynamics of isomerization reactions involving sugar phosphates. J. Biol. Chem. 1988, 263, 3664–3669. [Google Scholar] [PubMed]
- Goldberg, R.N. Thermodynamics of hexokinase-catalyzed reactions. Biophys. Chem. 1975, 3, 192–205. [Google Scholar] [CrossRef]
- Vogel, K.; Greinert, T.; Harms, H.; Sadowski, G.; Held, C.; Maskow, T. Influence of cytosolic conditions on the reaction equilibrium and the reaction enthalpy of the enolase reaction accessed by calorimetry and van ‘t HOFF. Biochim. Biophys. Acta (BBA) Gen. Subj. 2020, 1864, 129675. [Google Scholar] [CrossRef]
- Mazzei, L.; Ciurli, S.; Zambelli, B. Hot biological catalysis: Isothermal titration calorimetry to characterize enzymatic reactions. Jove J. Vis. Exp. 2014, 86, e51487. [Google Scholar] [CrossRef] [Green Version]
- Todd, M.J.; Gomez, J. Enzyme kinetics determined using calorimetry: A general assay for enzyme activity? Anal. Biochem. 2001, 296, 179–187. [Google Scholar] [CrossRef] [Green Version]
- Hansen, L.D.; Transtrum, M.K.; Quinn, C.; Demarse, N. Enzyme-catalyzed and binding reaction kinetics determined by titration calorimetry. Biochim. Biophys. Acta Gen. Subj. 2016, 1860, 957–966. [Google Scholar] [CrossRef]
- Demarse, N.A.; Killian, M.C.; Hansen, L.D.; Quinn, C.F. Determining enzyme kinetics via isothermal titration calorimetry. Methods Mol. Biol. 2013, 978, 21–30. [Google Scholar]
- Bianconi, M.L. Calorimetry of enzyme-catalyzed reactions. Biophys. Chem. 2007, 126, 59–64. [Google Scholar] [CrossRef]
- Lonhienne, T.G.; Winzor, D.J. A potential role for isothermal calorimetry in studies of the effects of thermodynamic non-ideality in enzyme-catalyzed reactions. J. Mol. Recognit. 2004, 17, 351–361. [Google Scholar] [CrossRef] [PubMed]
- Transtrum, M.K.; Hansen, L.D.; Quinn, C. Enzyme kinetics determined by single-injection isothermal titration calorimetry. Methods 2015, 76, 194–200. [Google Scholar] [CrossRef]
- Ladbury, J.E.; Chowdhry, B.Z. Sensing the heat: The application of isothermal titration calorimetry to thermodynamic studies of biomolecular interactions. Chem. Biol. 1996, 3, 791–801. [Google Scholar] [CrossRef] [Green Version]
- Mucsi, Z.; Szabó, A.; Hermecz, I.; Kucsman, Á.; Csizmadia, I.G. Modeling rate-controlling solvent effects. The pericyclic meisenheimer rearrangement of N-propargylmorpholine N-oxide. J. Am. Chem. Soc. 2005, 127, 7615–7631. [Google Scholar] [CrossRef] [PubMed]
- Ruff, F.; Csizmadia, I.G. Organic Reactions: Equilibria, Kinetics and Mechanism (Studies in Organic Chemistry); Elsevier: Amsterdam, The Netherlands, 1994. [Google Scholar]
- Reichardt, C.; Welton, T. Solvents and Solvent Effects in Organic Chemistry; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Maximova, K.; Wojtczak, J.; Trylska, J. Enzyme kinetics in crowded solutions from isothermal titration calorimetry. Anal. Biochem. 2019, 567, 96–105. [Google Scholar] [CrossRef] [PubMed]
- Norris, M.G.; Malys, N. What is the true enzyme kinetics in the biological system? An investigation of macromolecular crowding effect upon enzyme kinetics of glucose-6-phosphate dehydrogenase. Biochem. Biophys. Res. Commun. 2011, 405, 388–392. [Google Scholar] [CrossRef]
- Luby-Phelps, K. Cytoarchitecture and physical properties of cytoplasm: Volume, viscosity, diffusion, intracellular surface area. In International Review of Cytology; Elsevier: Amsterdam, The Netherlands, 1999; Volume 192, pp. 189–221. [Google Scholar]
- García-Contreras, R.; Vos, P.; Westerhoff, H.V.; Boogerd, F.C. Why in vivo may not equal in vitro—New effectors revealed by measurement of enzymatic activities under the same in vivo-like assay conditions. FEBS J. 2012, 279, 4145–4159. [Google Scholar]
- Slonczewski, J.L.; Fujisawa, M.; Dopson, M.; Krulwich, T.A. Cytoplasmic pH measurement and homeostasis in bacteria and archaea. Adv. Microb. Physiol. 2009, 55, 1–317. [Google Scholar]
- Ando, T.; Skolnick, J. Crowding and hydrodynamic interactions likely dominate in vivo macromolecular motion. Proc. Natl. Acad. Sci. USA 2010, 107, 18457–18462. [Google Scholar] [CrossRef] [Green Version]
- Theillet, F.X.; Binolfi, A.; Frembgen-Kesner, T.; Hingorani, K.; Sarkar, M.; Kyne, C.; Li, C.; Crowley, P.B.; Gierasch, L.; Pielak, G.J.; et al. Physicochemical properties of cells and their effects on intrinsically disordered proteins (IDPs). Chem. Rev. 2014, 114, 6661–6714. [Google Scholar] [CrossRef] [PubMed]
- Moomaw, A.S.; Maguire, M.E. The unique nature of Mg2+ channels. Physiology 2008, 23, 275–285. [Google Scholar] [CrossRef] [Green Version]
- Maguire, M.E.; Cowan, J.A. Magnesium chemistry and biochemistry. Biometals 2002, 15, 203–210. [Google Scholar] [CrossRef] [PubMed]
- Beeler, T.; Bruce, K.; Dunn, T. Regulation of cellular Mg2+ by Saccharomyces cerevisiae. Biochim. Biophys. Acta (BBA) Biomembr. 1997, 1323, 310–318. [Google Scholar] [CrossRef] [Green Version]
- Ellis, R.J. Macromolecular crowding: An important but neglected aspect of the intracellular environment. Curr. Opin. Struct. Biol. 2001, 11, 114–119. [Google Scholar] [CrossRef]
- Delarue, M.; Brittingham, G.P.; Pfeffer, S.; Surovtsev, I.V.; Pinglay, S.; Kennedy, K.J.; Schaffer, M.; Gutierrez, J.I.; Sang, D.; Poterewicz, G.; et al. mTORC1 controls phase separation and the biophysical properties of the cytoplasm by tuning crowding. Cell 2018, 174, 338–349.e20. [Google Scholar] [CrossRef] [Green Version]
- Vogel, K.; Greinert, T.; Harms, H.; Sadowski, G.; Held, C.; Maskow, T. Thermodynamics and kinetics of glycolytic reactions. Part I: Kinetic modeling based on irreversible thermodynamics and validation by calorimetry. Int. J. Mol. Sci. 2020. submitted. [Google Scholar]
- Noor, E.; Flamholz, A.; Liebermeister, W.; Bar-Even, A.; Milo, R. A note on the kinetics of enzyme action: A decomposition that highlights thermodynamic effects. FEBS Lett. 2013, 587, 2772–2777. [Google Scholar] [CrossRef] [Green Version]
- Beard, D.A.; Qian, H. Relationship between thermodynamic driving force and one-way fluxes in reversible processes. PLoS ONE 2007, 2, e144. [Google Scholar] [CrossRef] [Green Version]
- Bianconi, M.L. Calorimetric determination of thermodynamic parameters of reaction reveals different enthalpic compensations of the yeast hexokinase isozymes. J. Biol. Chem. 2003, 278, 18709–18713. [Google Scholar] [CrossRef] [Green Version]
- Morin, P.E.; Freire, E. Direct calorimetric analysis of the enzymatic activity of yeast cytochrome c oxidase. Biochemistry 1991, 30, 8494–8500. [Google Scholar] [CrossRef] [PubMed]
- Dyson, J.E.; Noltmann, E.A. The effect of pH and temperature on the kinetic parameters of phosphoglucose isomerase. Participation of histidine and lysine in a proposed dual function mechanism. J. Biol. Chem. 1968, 243, 1401–1414. [Google Scholar]
- Vojinovic, V.; von Stockar, U. Influence of uncertainties in pH, pMg, activity coefficients, metabolite concentrations, and other factors on the analysis of the thermodynamic feasibility of metabolic pathways. Biotechnol. Bioeng. 2009, 103, 780–795. [Google Scholar] [CrossRef] [PubMed]
- Alberty, R.A. Thermodynamics of Biochemical Reactions; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Bhat, R.; Timasheff, S.N. Steric exclusion is the principal source of the preferential hydration of proteins in the presence of polyethylene glycols. Protein Sci. 1992, 1, 1133–1143. [Google Scholar] [CrossRef] [Green Version]
- Arnold, K.; Herrmann, A.; Pratsch, L.; Gawrisch, K. The dielectric properties of aqueous solutions of poly (ethylene glycol) and their influence on membrane structure. Biochim. Biophys. Acta 1985, 815, 515–518. [Google Scholar] [CrossRef]
- Murthy, N.S.; Braswell, E.H.; Knox, J.R. The association behavior of β-lactamases in polyethylene glycol solution. Biopolym. Orig. Res. Biomol. 1988, 27, 865–881. [Google Scholar] [CrossRef]
- Honig, B.; Gilson, M. Calculation of the total electrostatic energy of a macromoleular system: Solvation energies, binding energies, and conformational analysis. Proteins 1988, 4, 7–18. [Google Scholar]
- Li, L.; Li, C.; Zhang, Z.; Alexov, E. On the dielectric “constant” of proteins: Smooth dielectric function for macromolecular modeling and its implementation in DelPhi. J. Chem. Theory Comput. 2013, 9, 2126–2136. [Google Scholar] [CrossRef]
- Alexov, E.; Mehler, E.L.; Baker, N.; Baptista, A.M.; Huang, Y.; Milletti, F.; Nielsen, J.E.; Farrell, D.; Carstensen, T.; Olsson, M.H.; et al. Progress in the prediction of pKa values in proteins. Proteins 2011, 79, 3260–3275. [Google Scholar] [CrossRef] [Green Version]
- Shabala, L.; Bowman, J.; Brown, J.; Ross, T.; McMeekin, T.; Shabala, S. Ion transport and osmotic adjustment in Escherichia coli in response to ionic and non-ionic osmotica. Environ. Microbiol. 2009, 11, 137–148. [Google Scholar] [CrossRef]
- Junker, N.O.; Vaghefikia, F.; Albarghash, A.; Hofig, H.; Kempe, D.; Walter, J.; Otten, J.; Pohl, M.; Katranidis, A.; Wiegand, S.; et al. Impact of molecular crowding on translational mobility and conformational properties of biological macromolecules. J. Phys. Chem. B 2019, 123, 4477–4486. [Google Scholar] [CrossRef] [PubMed]
- Rohwer, J.M.; Postma, P.W.; Kholodenko, B.N.; Westerhoff, H.V. Implications of macromolecular crowding for signal transduction and metabolite channeling. Proc. Natl. Acad. Sci. USA 1998, 95, 10547–10552. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pastor, I.; Pitulice, L.; Balcells, C.; Vilaseca, E.; Madurga, S.; Isvoran, A.; Cascante, M.; Mas, F. Effect of crowding by Dextrans in enzymatic reactions. Biophys. Chem. 2014, 185, 8–13. [Google Scholar] [CrossRef] [Green Version]
- Balcells, C.; Pastor, I.; Vilaseca, E.; Madurga, S.; Cascante, M.; Mas, F. Macromolecular crowding effect upon in vitro enzyme kinetics: Mixed activation-diffusion control of the oxidation of NADH by pyruvate catalyzed by lactate dehydrogenase. J. Phys. Chem. B 2014, 118, 4062–4068. [Google Scholar] [CrossRef] [Green Version]
- Miermont, A.; Waharte, F.; Hu, S.Q.; McClean, M.N.; Bottani, S.; Leon, S.; Hersen, P. Severe osmotic compression triggers a slowdown of intracellular signaling, which can be explained by molecular crowding. Proc. Natl. Acad. Sci. USA 2013, 110, 5725–5730. [Google Scholar] [CrossRef] [Green Version]
- Ellis, R.J. Macromolecular crowding: Obvious but underappreciated. Trends Biochem. Sci. 2001, 26, 597–604. [Google Scholar] [CrossRef]
- Minton, A.P. The influence of macromolecular crowding and macromolecular confinement on biochemical reactions in physiological media. J. Biol. Chem. 2001, 276, 10577–10580. [Google Scholar] [CrossRef] [Green Version]
- Hines, M.C.; Wolfe, R.G. Phosphoglucose isomerase. 2. Influence of PH on kinetic parameters. Biochemistry 1963, 2, 770–775. [Google Scholar] [CrossRef]
- Vennemann, N.; Lechner, M.; Oberthür, R. Thermodynamics and conformation of polyoxyethylene in aqueous solution under high pressure: 1. Small-angle neutron scattering and densitometric measurements at room temperature. Polymer 1987, 28, 1738–1748. [Google Scholar] [CrossRef]
- Westhead, E.W.; McLain, G. A purification of brewers’ and bakers’ yeast enolase yielding a single active component. J. Biol. Chem. 1964, 239, 2464–2468. [Google Scholar]
- Schurig, H.; Rutkat, K.; Rachel, R.; Jaenicke, R. Octameric enolase from the hyperthermophilic bacterium Thermotoga-maritima—Purification, characterization, and image-processing. Protein Sci. 1995, 4, 228–236. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kornblatt, M.J.; Klugerman, A. Characterization of the enolase isozymes of rabbit brain—Kinetic differences between mammalian and yeast enolases. Biochem. Cell Biol. Biochim. Biol. Cell. 1989, 67, 103–107. [Google Scholar] [CrossRef] [PubMed]
- Wold, F.; Ballou, C.E. Studies on the enzyme enolase. 1. Equilibrium studies. J. Biol. Chem. 1957, 227, 301–312. [Google Scholar] [PubMed]
- Warburg, O. Isolierung und kristallisation des gaerungsferments enolase. Biochem. Z. 1941, 310, 384–421. [Google Scholar]
- Wold, F.; Ballou, C.E. Studies on the enzyme enolase. II. Kinetic studies. J. Biol. Chem. 1957, 227, 313–328. [Google Scholar] [PubMed]
- Held, C.; Reschke, T.; Mohammad, S.; Luza, A.; Sadowski, G. ePC-SAFT revised. Chem. Eng. Res. Des. 2014, 92, 2884–2897. [Google Scholar] [CrossRef]
- Gross, J.; Sadowski, G. Perturbed-chain SAFT: An equation of state based on a perturbation theory for chain molecules. Ind. Eng. Chem. Res. 2001, 40, 1244–1260. [Google Scholar] [CrossRef]
- Cameretti, L.F.; Sadowski, G.; Mollerup, J.M. Modeling of aqueous electrolyte solutions with perturbed-chain statistical associated fluid theory. Ind. Eng. Chem. Res. 2005, 44, 3355–3362. [Google Scholar] [CrossRef]
- Lorentz, H. Ueber die Anwendung des Satzes vom Virial in der kinetischen Theorie der Gase. Annalen Physik 1881, 248, 127–136. [Google Scholar] [CrossRef] [Green Version]
- Wolbach, J.P.; Sandler, S.I. Using molecular orbital calculations to describe the phase behavior of hydrogen-bonding fluids. Ind. Eng. Chem. Res. 1997, 36, 4041–4051. [Google Scholar] [CrossRef]
- Greinert, T.; Vogel, K.; Seifert, A.I.; Siewert, R.; Andreeva, I.V.; Verevkin, S.P.; Maskow, T.; Sadowski, G.; Held, C. Standard Gibbs energy of metabolic reactions: V. Enolase reaction. Biochim. Biophys. Acta (BBA)-Proteins Proteom. 2020, 1868, 140365. [Google Scholar] [CrossRef] [PubMed]
- Wangler, A.; Schmidt, C.; Sadowski, G.; Held, C. Standard Gibbs energy of metabolic reactions: III the 3-phosphoglycerate kinase reaction. ACS Omega 2018, 3, 1783–1790. [Google Scholar] [CrossRef]
- Fuchs, D.; Fischer, J.; Tumakaka, F.; Sadowski, G. Solubility of amino acids: Influence of the pH value and the addition of alcoholic cosolvents on aqueous solubility. Ind. Eng. Chem. Res. 2006, 45, 6578–6584. [Google Scholar] [CrossRef]




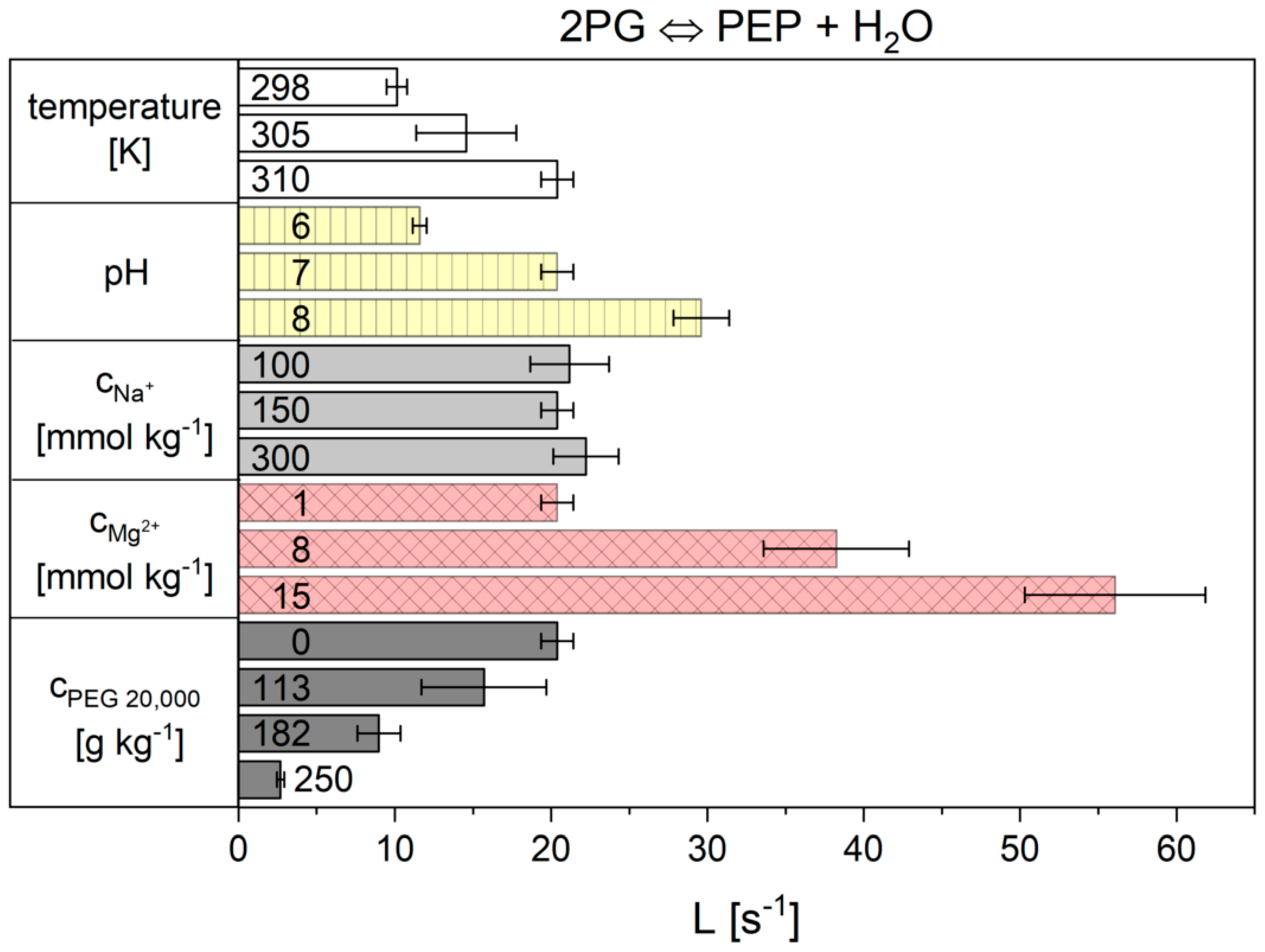
| pH | ||
|---|---|---|
| 6 | 9.6 ± 0.2 kJ mol−1 (86 ± 2%) | 13.2 kJ mol−1 (91%) |
| 7 | 11.1 ± 0.5 kJ mol−1 (100%) | 14.5 kJ mol−1 (100%) |
| 8 | 10.8 ± 0.3 kJ mol−1 (97 ± 3%) | 14.7 kJ mol−1 (101%) |
| Gibbs Free Energy Change (kJ mol−1) | Reaction Enthalpy Change (kJ mol−1) | Entropy Change (J mol−1 K−1) | ||||
|---|---|---|---|---|---|---|
| Conditions | Reaction 2 | Reaction 9 | Reaction 2 | Reaction 9 From [6] | Reaction 2 | Reaction 9 From [6] |
| basic condition | 2.8 ± 0.1 | −13.7 ± 0.1 | 11.1 ± 0.5 | 2.4 ± 0.1 | 26.9 ± 1.7 | 51.8 ± 0.5 |
| 250 g L−1 PEG 20,000 | 12.8 ± 2.9 | −10.8 ± 0.1 | 7.8 ± 0.3 | 0.7 ± 0.0 | −15.9 ± 1.1 | 34.7 ± 0.8 |
| 250 g L−1 PEG 6000 | 12.8 ± 2.9 | n.d. | 7.7 ± 0.1 | n.d. | −16.4 ± 0.4 | n.d. |
| 250 g L−1 BSA | 6.4 ± 0.2 | n.d. | 7.4 ± 1.0 | n.d. | 3.1 ± 3.6 | n.d. |
| Conditions | Chemicals | Values | Unit |
|---|---|---|---|
| Temperature | - | 298.15, 305.15, 310.15 | K |
| pH | buffer | 6, 7, 8 | - |
| Na+ concentration | NaOH, NaCl | 0.1, 0.15, 0.3 | mol kg−1 |
| Mg2+ concentration | MgCl2 | 1, 8, 15 | mmol kg−1 |
| Crowding agent concentration | PEG 20,000 PEG 6000 BSA | 0, 113, 182, 250 250 250 | g kg−1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vogel, K.; Greinert, T.; Reichard, M.; Held, C.; Harms, H.; Maskow, T. Thermodynamics and Kinetics of Glycolytic Reactions. Part II: Influence of Cytosolic Conditions on Thermodynamic State Variables and Kinetic Parameters. Int. J. Mol. Sci. 2020, 21, 7921. https://0-doi-org.brum.beds.ac.uk/10.3390/ijms21217921
Vogel K, Greinert T, Reichard M, Held C, Harms H, Maskow T. Thermodynamics and Kinetics of Glycolytic Reactions. Part II: Influence of Cytosolic Conditions on Thermodynamic State Variables and Kinetic Parameters. International Journal of Molecular Sciences. 2020; 21(21):7921. https://0-doi-org.brum.beds.ac.uk/10.3390/ijms21217921
Chicago/Turabian StyleVogel, Kristina, Thorsten Greinert, Monique Reichard, Christoph Held, Hauke Harms, and Thomas Maskow. 2020. "Thermodynamics and Kinetics of Glycolytic Reactions. Part II: Influence of Cytosolic Conditions on Thermodynamic State Variables and Kinetic Parameters" International Journal of Molecular Sciences 21, no. 21: 7921. https://0-doi-org.brum.beds.ac.uk/10.3390/ijms21217921