Integrative Analysis of Multi-Omics Data Based on Blockwise Sparse Principal Components
Abstract
:1. Introduction
2. Results
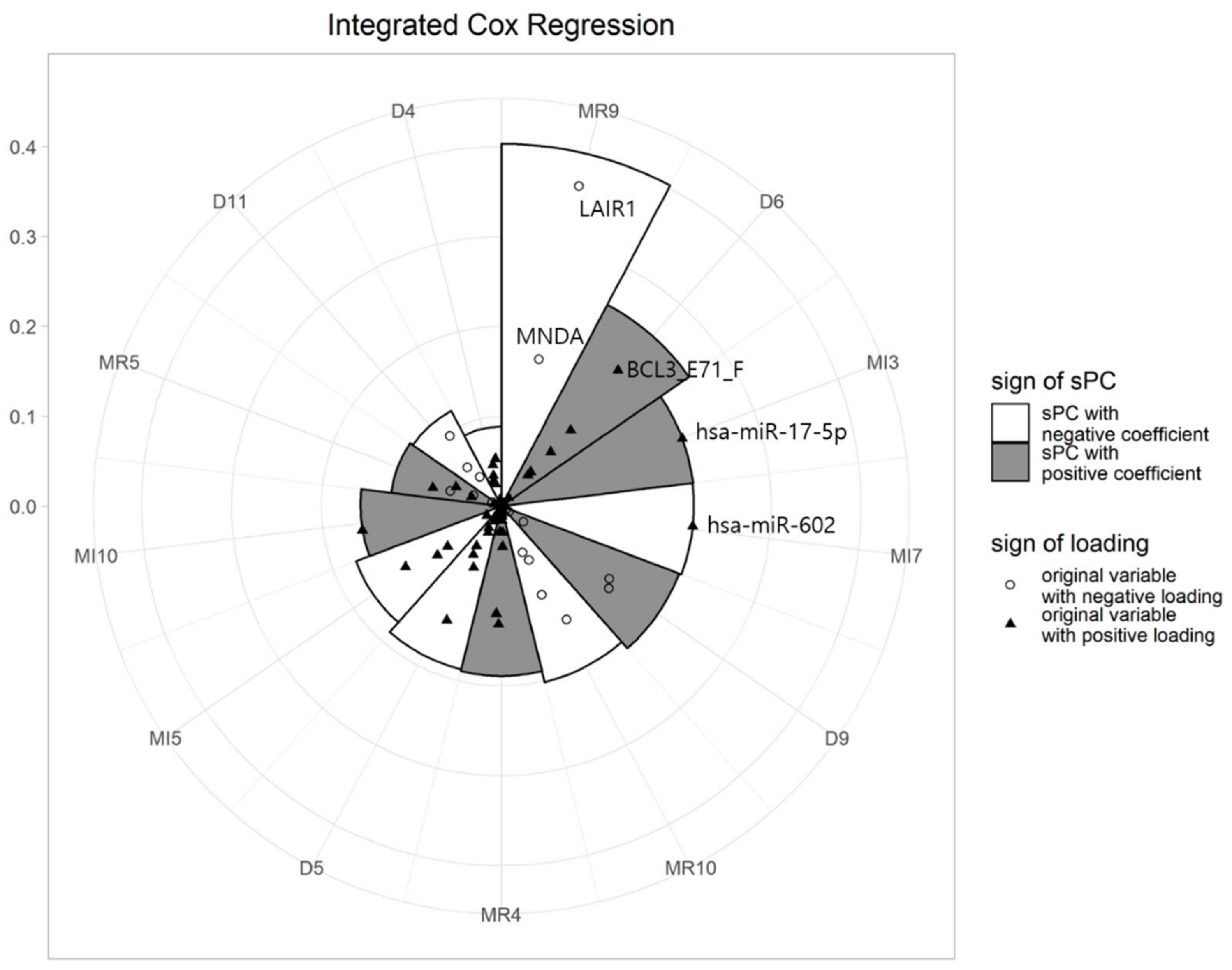
2.1. Analysis Using iMO-BSPC
2.2. Comparison with Other Approaches
3. Discussion
4. Materials and Methods
4.1. Stage 1: Finding Blockwise Components for Each Omics Data
4.1.1. Finding Homogeneous Variable Blocks
4.1.2. Extracting Sparse Principal Components
4.2. Stage 2: Integrative Analysis for Multi-Omics Data
4.2.1. Parallel Integration of Omics Data, and Construction of a Prediction Model
4.2.2. Assessing Prediction Performance
4.2.3. Visualization
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AIC | Akaike information criterion |
| AUC | Area under the curve |
| GBM | Glioblastoma multiforme |
| HR | Hazard ratio |
| iMO-BSPC | Integrative analysis of multi-omics data based on block-wise sparse principal component analysis |
| LASSO | least absolute shrinkage and selection operator |
| MP chart | Multi-level polar chart |
| PCA | Principal component analysis |
| PLS | Partial least squares |
| ROC curve | Receiver operator characteristic curve |
| SAS | Statistical analysis system |
| sPC | Sparse principal component |
| TCGA | The Cancer Genome Atlas |
References
- Shafi, A.; Nguyen, T.; Peyvandipour, A.; Nguyen, H.; Draghici, S. A Multi-Cohort and Multi-Omics Meta-Analysis Framework to Identify Network–Based Gene Signatures. Front. Genet. 2019, 10, 159. [Google Scholar] [CrossRef]
- Greenawalt, D.M.; Sieberts, S.K.; Cornelis, M.C.; Girman, C.J.; Zhong, H.; Yang, X.; Guinney, J.; Qi, L.; Hu, F.B. Integrating genetic association, genetics of gene expression, and single nucleotide polymorphism set analysis to identify susceptibility Loci for type 2 diabetes mellitus. Am. J. Epidemiol. 2012, 176, 423–430. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Karczewski, K.J.; Snyder, M.P. Integrative omics for health and disease. Nat. Rev. Genet. 2018, 19, 299–310. [Google Scholar] [CrossRef] [PubMed]
- Meng, C.; Zeleznik, O.A.; Thallinger, G.G.; Kuster, B.; Gholami, A.M.; Culhane, A.C. Dimension reduction techniques for the integrative analysis of multi-omics data. Brief. Bioinform. 2016, 17, 628–641. [Google Scholar] [CrossRef] [PubMed]
- Abraham, G.; Inouye, M. Fast principal component analysis of large-scale genome-wide data. PLoS ONE 2014, 9, e93766. [Google Scholar] [CrossRef] [Green Version]
- Patterson, N.; Price, A.L.; Reich, D. Population structure and eigenanalysis. PLoS Genet. 2006, 2, e190. [Google Scholar] [CrossRef]
- Alonso–Gutierrez, J.; Kim, E.-M.; Batth, T.S.; Cho, N.; Hu, Q.; Chan, L.J.G.; Petzold, C.J.; Hillson, N.J.; Adams, P.D.; Keasling, J.D.; et al. Principal component analysis of proteomics (PCAP) as a tool to direct metabolic engineering. Metab. Eng. 2015, 28, 123–133. [Google Scholar]
- Ringnér, M. What is principal component analysis? Nat. Biotechnol. 2008, 26, 303–304. [Google Scholar] [CrossRef] [PubMed]
- Bougeard, S.; Abdi, H.; Saporta, G.; Niang, N. Clusterwise analysis for multiblock component methods. Adv. Data Anal. Classif. 2018, 12, 285–313. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T.; Tibshirani, R. Sparse Principal Component Analysis. J. Comput. Graph. Stat. 2006, 15, 265–286. [Google Scholar] [CrossRef] [Green Version]
- Cadima, J.; Jolliffe, I.T. Loading and correlations in the interpretation of principle compenents. J. Appl. Stat. 1995, 22, 203–214. [Google Scholar] [CrossRef]
- Yu, L.; Liu, H. Efficient feature selection via analysis of relevance and redundancy. J. Mach. Learn. Res. 2004, 5, 1205–1224. [Google Scholar]
- Venkatesh, B.; Anuradha, J. A review of feature selection and its methods. Cybern. Inf. Technol. 2019, 19, 3–26. [Google Scholar] [CrossRef] [Green Version]
- Kristensen, V.N.; Lingjærde, O.C.; Russnes, H.G.; Vollan, H.K.M.; Frigessi, A.; Børresen–Dale, A. –L. Principles and methods of integrative genomic analyses in cancer. Nat. Rev. Cancer 2014, 14, 299. [Google Scholar] [CrossRef] [PubMed]
- Pineda, S.; Real, F.X.; Kogevinas, M.; Carrato, A.; Chanock, S.J.; Malats, N.; Van Steen, K. Integration Analysis of Three Omics Data Using Penalized Regression Methods: An Application to Bladder Cancer. PLoS Genet. 2015, 11, e1005689. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Richardson, S.; Tseng, G.C.; Sun, W. Statistical Methods in Integrative Genomics. Annu. Rev. Stat. Appl. 2016, 3, 181–209. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Thompson, J.R.; Attia, J.; Minelli, C. The meta-analysis of genome-wide association studies. Brief. Bioinform. 2011, 12, 259–269. [Google Scholar] [CrossRef]
- Begum, F.; Ghosh, D.; Tseng, G.C.; Feingold, E. Comprehensive literature review and statistical considerations for GWAS meta-analysis. Nucleic Acids Res. 2012, 40, 3777–3784. [Google Scholar] [CrossRef] [Green Version]
- Wu, C.; Zhou, F.; Ren, J.; Li, X.; Jiang, Y.; Ma, S. A Selective Review of Multi-Level Omics Data Integration Using Variable Selection. High Throughput 2019, 8, 4. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Q.; Shi, X.; Xie, Y.; Huang, J.; Shia, B.; Ma, S. Combining multidimensional genomic measurements for predicting cancer prognosis: Observations from TCGA. Brief. Bioinform. 2014, 16, 291–303. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Y.; Shi, X.; Zhao, Q.; Krauthammer, M.; Rothberg, B.E.G.; Ma, S. Integrated analysis of multidimensional omics data on cutaneous melanoma prognosis. Genomics 2016, 107, 223–230. [Google Scholar] [CrossRef] [PubMed]
- Zou, H. The Adaptive Lasso and Its Oracle Properties. J. Am. Stat. Assoc. 2006, 101, 1418–1429. [Google Scholar] [CrossRef] [Green Version]
- Fan, J.; Li, R. Variable Selection via Nonconcave Penalized Likelihood and its Oracle Properties. J. Am. Stat. Assoc. 2001, 96, 1348–1360. [Google Scholar] [CrossRef]
- Zhang, C.-H. Nearly unbiased variable selection under minimax concave penalty. Ann. Stat. 2010, 38, 894–942. [Google Scholar] [CrossRef] [Green Version]
- Wu, C.; Ma, S. A selective review of robust variable selection with applications in bioinformatics. Brief Bioinform. 2015, 16, 873–883. [Google Scholar] [CrossRef] [Green Version]
- Ickstadt, K.; Schäfer, M.; Zucknick, M. Toward Integrative Bayesian Analysis in Molecular Biology. Annu. Rev. Stat. Its Appl. 2018, 5, 141–167. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Hassani, S.; Martens, H.; Qannari, E.M.; Hanafi, M.; Borge, G.I.; Kohler, A. Analysis of -omics data: Graphical interpretation– and validation tools in multi–block methods. Chemom. Intell. Lab. Syst. 2010, 104, 140–153. [Google Scholar] [CrossRef]
- Hassani, S.; Hanafi, M.; Qannari, E.M.; Kohler, A. Deflation strategies for multi-block principal component analysis revisited. Chemom. Intell. Lab. Syst. 2013, 120, 154–168. [Google Scholar] [CrossRef]
- Yang, Z.; Michailidis, G. A non-negative matrix factorization method for detecting modules in heterogeneous omics multi-modal data. Bioinformatics 2016, 32, 1–8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Waaijenborg, S.; Zwinderman, A.H. Sparse canonical correlation analysis for identifying, connecting and completing gene–expression networks. Bmc Bioinform. 2009, 10, 315. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Z.; Safo, S.E.; Long, Q. Incorporating biological information in sparse principal component analysis with application to genomic data. BMC Bioinform. 2017, 18, 332. [Google Scholar] [CrossRef]
- Lock, E.F.; Hoadley, K.A.; Marron, J.S.; Nobel, A.B. Joint and individual variation explained (jive) for integrated analysis of multiple data types. Ann. Appl. Stat. 2013, 7, 523–542. [Google Scholar] [CrossRef]
- Li, Y.; Wu, F.X.; Ngom, A. A review on machine learning principles for multi–view biological data integration. Brief Bioinform. 2018, 19, 325–340. [Google Scholar] [CrossRef]
- Shen, R.; Olshen, A.B.; Ladanyi, M. Integrative clustering of multiple genomic data types using a joint latent variable model with application to breast and lung cancer subtype analysis. Bioinformatics 2009, 25, 2906–2912. [Google Scholar] [CrossRef]
- Wang, W.; Baladandayuthapani, V.; Morris, J.S.; Broom, B.M.; Manyam, G.; Do, K.-A. iBAG: Integrative Bayesian analysis of high–dimensional multiplatform genomics data. Bioinformatics 2013, 29, 149–159. [Google Scholar] [CrossRef]
- Subramanian, I.; Verma, S.; Kumar, S.; Jere, A.; Anamika, K. Multi-omics Data Integration, Interpretation, and Its Application. Bioinform. Biol. Insights 2020, 14, 1177932219899051. [Google Scholar] [CrossRef] [Green Version]
- Qi, X.; Luo, R.; Zhao, H. Sparse principal component analysis by choice of norm. J. Multivar. Anal. 2013, 114, 127–160. [Google Scholar] [CrossRef]
- Huh, M.-H. Representing variables in the latent space. Korean J. Appl. Stat. 2017, 30, 555–566. [Google Scholar] [CrossRef] [Green Version]
- Dhillon, I.S.; Marcotte, E.M.; Roshan, U. Diametrical clustering for identifying anti-correlated gene clusters. Bioinformatics 2003, 19, 1612–1619. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kiers, H.A. Simple structure in component analysis techniques for mixtures of qualitative and quantitative variables. Psychometrika 1991, 56, 197–212. [Google Scholar] [CrossRef]
- Wang, Q. Kernel principal component analysis and its applications in face recognition and active shape models. arXiv 2012, preprint. arXiv:1207.3538. [Google Scholar]
- Wang, Y.; Zhang, X.; Miao, F.; Cao, Y.; Xue, J.; Cao, Q.; Zhang, X. Clinical significance of leukocyte-associated immunoglobulin-like receptor-1 expression in human cervical cancer. Exp. Ther. Med. 2016, 12, 3699–3705. [Google Scholar] [CrossRef] [Green Version]
- Xu, L.; Wang, S.; Li, J.; Li, J.; Li, B. Cancer immunotherapy based on blocking immune suppression mediated by an immune modulator LAIR–1. OncoImmunology 2020, 9, 1740477. [Google Scholar] [CrossRef] [Green Version]
- Guo, Q.; Guan, G.F.; Cao, J.Y.; Zou, C.Y.; Zhu, C.; Cheng, W.; Xu, X.Y.; Lin, Z.G.; Cheng, P.; Wu, A.H. Overexpression of oncostatin M receptor regulates local immune response in glioblastoma. J. Cell. Physiol. 2019, 234, 15496–15509. [Google Scholar] [CrossRef]
- Liu, Y.; Ma, L.; Shangguan, F.; Zhao, X.; Wang, W.; Gao, Z.; Zhou, H.; Qu, G.; Huang, Y.; An, J. LAIR–1 suppresses cell growth of ovarian cancer cell via the PI3K–AKT–mTOR pathway. Aging 2020, 12, 16142. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, L.; Zhou, J.; Liu, L.; Fu, Q.; Fu, A.; Feng, X.; Xin, R.; Liu, H.; Gao, Y. Clinicopathologic significance of LAIR–1 expression in hepatocellular carcinoma. Curr. Probl. Cancer 2019, 43, 18–26. [Google Scholar] [CrossRef]
- Briggs, R.C.; Atkinson, J.B.; Miranda, R.N. Variable expression of human myeloid specific nuclear antigen MNDA in monocyte lineage cells in atherosclerosis. J. Cell. Biochem. 2005, 95, 293–301. [Google Scholar] [CrossRef]
- North, W.G.; Liu, F.; Lin, L.Z.; Tian, R.; Akerman, B. NMDA receptors are important regulators of pancreatic cancer and are potential targets for treatment. Clin. Pharmacol. Adv. Appl. 2017, 9, 79. [Google Scholar] [CrossRef] [Green Version]
- Sun, C.; Liu, C.; Dong, J.; Li, D.; Li, W. Effects of the myeloid cell nuclear differentiation antigen on the proliferation, apoptosis and migration of osteosarcoma cells. Oncol. Lett. 2014, 7, 815–819. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Peng, Q.; Li, R.; Li, Y.; Xu, X.; Ni, W.; Lin, H.; Ning, L. Prediction of a competing endogenous RNA co-expression network as a prognostic marker in glioblastoma. J. Cell. Mol. Med. 1–10. [CrossRef] [PubMed]
- Wu, L.; Bernal, G.M.; Cahill, K.E.; Pytel, P.; Fitzpatrick, C.A.; Mashek, H.; Weichselbaum, R.R.; Yamini, B. BCL3 expression promotes resistance to alkylating chemotherapy in gliomas. Sci. Transl. Med. 2018, 10, eaar2238. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, K.; Cui, X.; Wang, Q.; Fang, C.; Tan, Y.; Wang, Y.; Yi, K.; Yang, C.; You, H.; Shang, R. RUNX1 contributes to the mesenchymal subtype of glioblastoma in a TGFβ pathway–dependent manner. Cell Death Dis. 2019, 10, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Zhou, C.; Huang, Y.; Chen, Y.; Xie, Y.; Wen, H.; Tan, W.; Wang, C. miR–602 Mediates the RASSF1A/JNK Pathway, Thereby Promoting Postoperative Recurrence in Nude Mice with Liver Cancer. Oncotargets Ther. 2020, 13, 6767. [Google Scholar] [CrossRef]
- Li, R.; Gao, K.; Luo, H.; Wang, X.; Shi, Y.; Dong, Q.; Luan, W.; You, Y. Identification of intrinsic subtype–specific prognostic microRNAs in primary glioblastoma. J. Exp. Clin. Cancer Res. 2014, 33, 9. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Ma, Z.; Wang, D.; Zhao, W.; Chen, L.; Wang, G. MicroRNA–602 regulating tumor suppressive gene RASSF1A is over–expressed in hepatitis B virus–infected liver and hepatocellular carcinoma. Cancer Biol. Ther. 2010, 9, 803–808. [Google Scholar] [CrossRef] [Green Version]
- Tsz–fung, F.C.; Mankaruos, M.; Scorilas, A.; Youssef, Y.; Girgis, A.; Mossad, S.; Metias, S.; Rofael, Y.; Honey, R.J.; Stewart, R. The miR–17–92 cluster is over expressed in and has an oncogenic effect on renal cell carcinoma. J. Urol. 2010, 183, 743–751. [Google Scholar]
- Fu, F.; Jiang, W.; Zhou, L.; Chen, Z. Circulating exosomal miR–17–5p and miR–92a–3p predict pathologic stage and grade of colorectal cancer. Transl. Oncol. 2018, 11, 221–232. [Google Scholar] [CrossRef]
- Agnihotri, S.; Burrell, K.E.; Wolf, A.; Jalali, S.; Hawkins, C.; Rutka, J.T.; Zadeh, G. Glioblastoma, a brief review of history, molecular genetics, animal models and novel therapeutic strategies. Arch. Immunol. Ther. Exp. 2013, 61, 25–41. [Google Scholar] [CrossRef]
- Sayegh, E.T.; Kaur, G.; Bloch, O.; Parsa, A.T. Systematic review of protein biomarkers of invasive behavior in glioblastoma. Mol. Neurobiol. 2014, 49, 1212–1244. [Google Scholar] [CrossRef]
- SAS Institute. SAS/STAT12.1; SAS Institute, Inc.: Cary, NC, USA, 2012; pp. 8497–8529. [Google Scholar]
- Vigneau, E.; Qannari, E. Clustering of variables around latent components. Commun. Stat. Simul. Comput. 2003, 32, 1131–1150. [Google Scholar] [CrossRef]
- Chavent, M.; Kuentz–Simonet, V.; Liquet, B.; Saracco, J. ClustOfVar: An R Package for the Clustering of Variables. arXiv 2012, arXiv:1112.0295. [Google Scholar]
- Feng, C.-M.; Gao, Y.-L.; Liu, J.-X.; Zheng, C.-H.; Li, S.-J.; Wang, D. A Simple Review of Sparse Principal Components Analysis, Proceedings of the International Conference on Intelligent Computing, Lanzhou, China, 2–5 August 2016; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Wolf, P.; Schmidt, G.; Ulm, K. The use of ROC for defining the validity of the prognostic index in censored data. Stat. Probab. Lett. 2011, 81, 783–791. [Google Scholar] [CrossRef] [Green Version]
- Heagerty, P.J.; Zheng, Y. Survival model predictive accuracy and ROC curves. Biometrics 2005, 61, 92–105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Harrell, F.E., Jr.; Califf, R.M.; Pryor, D.B.; Lee, K.L.; Rosati, R.A. Evaluating the Yield of Medical Tests. JAMA 1982, 247, 2543–2546. [Google Scholar] [CrossRef]
- Schmid, M.; Wright, M.N.; Ziegler, A. On the use of Harrell’s C for clinical risk prediction via random survival forests. Expert Syst. Appl. 2016, 63, 450–459. [Google Scholar] [CrossRef] [Green Version]
- Raykar, V.C.; Steck, H.; Krishnapuram, B.; Dehing–Oberije, C.; Lambin, P. On Ranking in Survival Analysis: Bounds on the Concordance Index. In Proceedings of the 20th International Conference on Neural Information Processing Systems, Daegu, Korea, 3–7 November 2013; Curran Associates Inc.: Vancouver, BC, Canada, 2007; pp. 1209–1216. [Google Scholar]





| Omics | Block | Number of Variables | Number of Variables Remained | Coefficient (Standard Error) | Hazard Ratio | 1p-Value |
|---|---|---|---|---|---|---|
| DNA | D4 | 128 | 13 | −0.09 (0.05) | 0.92 | 0.089 |
| D5 | 186 | 19 | −0.19 (0.05) | 0.83 | <0.001 | |
| D6 | 153 | 15 | 0.25 (0.06) | 1.29 | <0.001 | |
| D9 | 69 | 7 | 0.21 (0.07) | 1.24 | 0.004 | |
| D11 | 46 | 5 | −0.12 (0.05) | 0.89 | 0.011 | |
| mRNA | MR4 | 188 | 19 | 0.19 (0.07) | 1.21 | 0.009 |
| MR5 | 161 | 16 | 0.12 (0.06) | 1.13 | 0.033 | |
| MR9 | 65 | 6 | −0.40 (0.10) | 0.67 | <0.001 | |
| MR10 | 67 | 7 | −0.20 (0.07) | 0.82 | 0.011 | |
| miRNA | MI3 | 32 | 3 | 0.21 (0.08) | 1.24 | 0.005 |
| MI5 | 79 | 8 | −0.17 (0.05) | 0.84 | <0.001 | |
| MI7 | 56 | 6 | −0.21 (0.09) | 0.81 | 0.021 | |
| MI10 | 22 | 2 | 0.16 (0.06) | 1.17 | 0.016 |
| Methodology | Single Omics | Multi-Omics | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (1) | (2) | (3) | |||||||
| Omics | (a) | (b) | (c) | (a) | (b) | (c) | (a) | (b) | (c) | all | all | all |
| 1 PC-before | 12 | 10 | 10 | 12 | 10 | 10 | 12 | 10 | 10 | 32 | 32 | 32 |
| 2 PC-after | 5 | 2 | 2 | 8 | 4 | 3 | 4 | 4 | 3 | 13 | 15 | 13 |
| 3 variable | 563 | 188 | 225 | 935 | 559 | 167 | 56 | 49 | 17 | 1580 | 1339 | 126 |
| AUC | 0.67 | 0.54 | 0.61 | 0.71 | 0.58 | 0.59 | 0.66 | 0.60 | 0.63 | 0.75 | 0.76 | 0.74 |
| C-index | 0.63 | 0.55 | 0.60 | 0.64 | 0.61 | 0.60 | 0.61 | 0.59 | 0.60 | 0.69 | 0.69 | 0.67 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, M.; Kim, D.; Moon, K.; Park, T. Integrative Analysis of Multi-Omics Data Based on Blockwise Sparse Principal Components. Int. J. Mol. Sci. 2020, 21, 8202. https://0-doi-org.brum.beds.ac.uk/10.3390/ijms21218202
Park M, Kim D, Moon K, Park T. Integrative Analysis of Multi-Omics Data Based on Blockwise Sparse Principal Components. International Journal of Molecular Sciences. 2020; 21(21):8202. https://0-doi-org.brum.beds.ac.uk/10.3390/ijms21218202
Chicago/Turabian StylePark, Mira, Doyoen Kim, Kwanyoung Moon, and Taesung Park. 2020. "Integrative Analysis of Multi-Omics Data Based on Blockwise Sparse Principal Components" International Journal of Molecular Sciences 21, no. 21: 8202. https://0-doi-org.brum.beds.ac.uk/10.3390/ijms21218202





