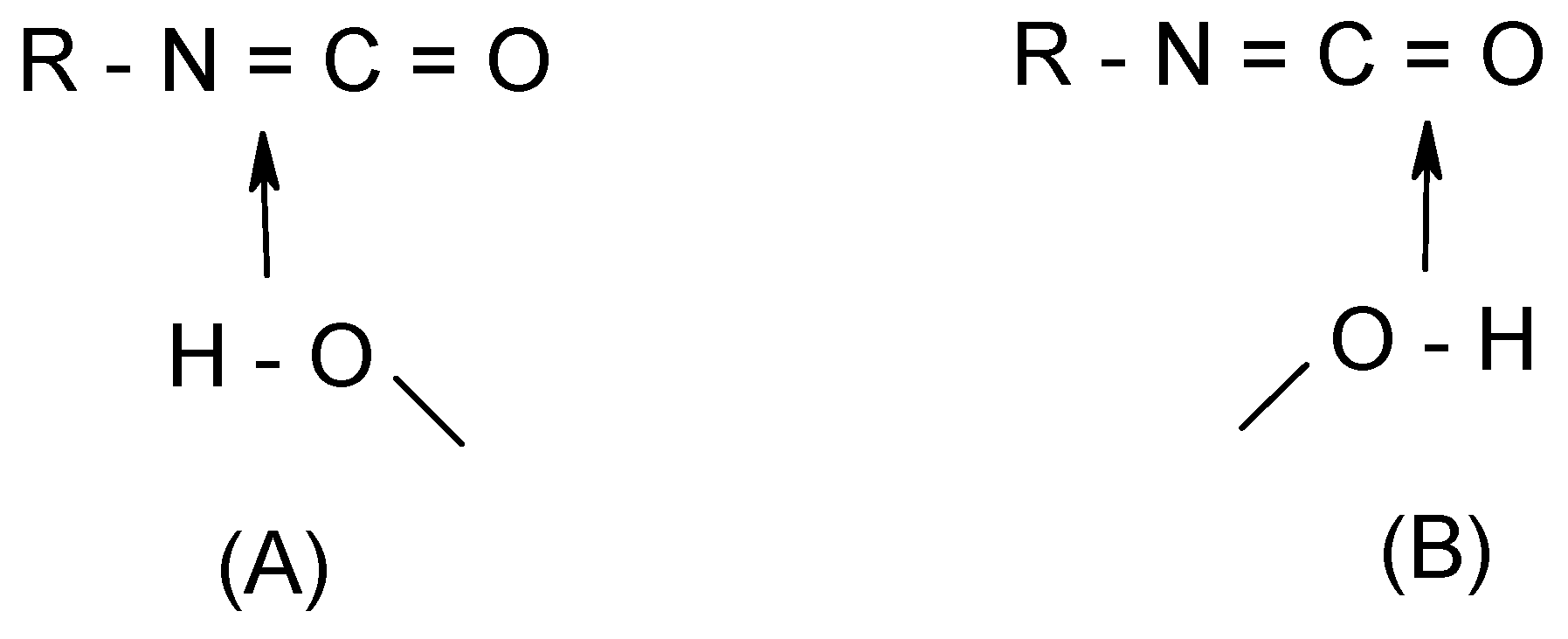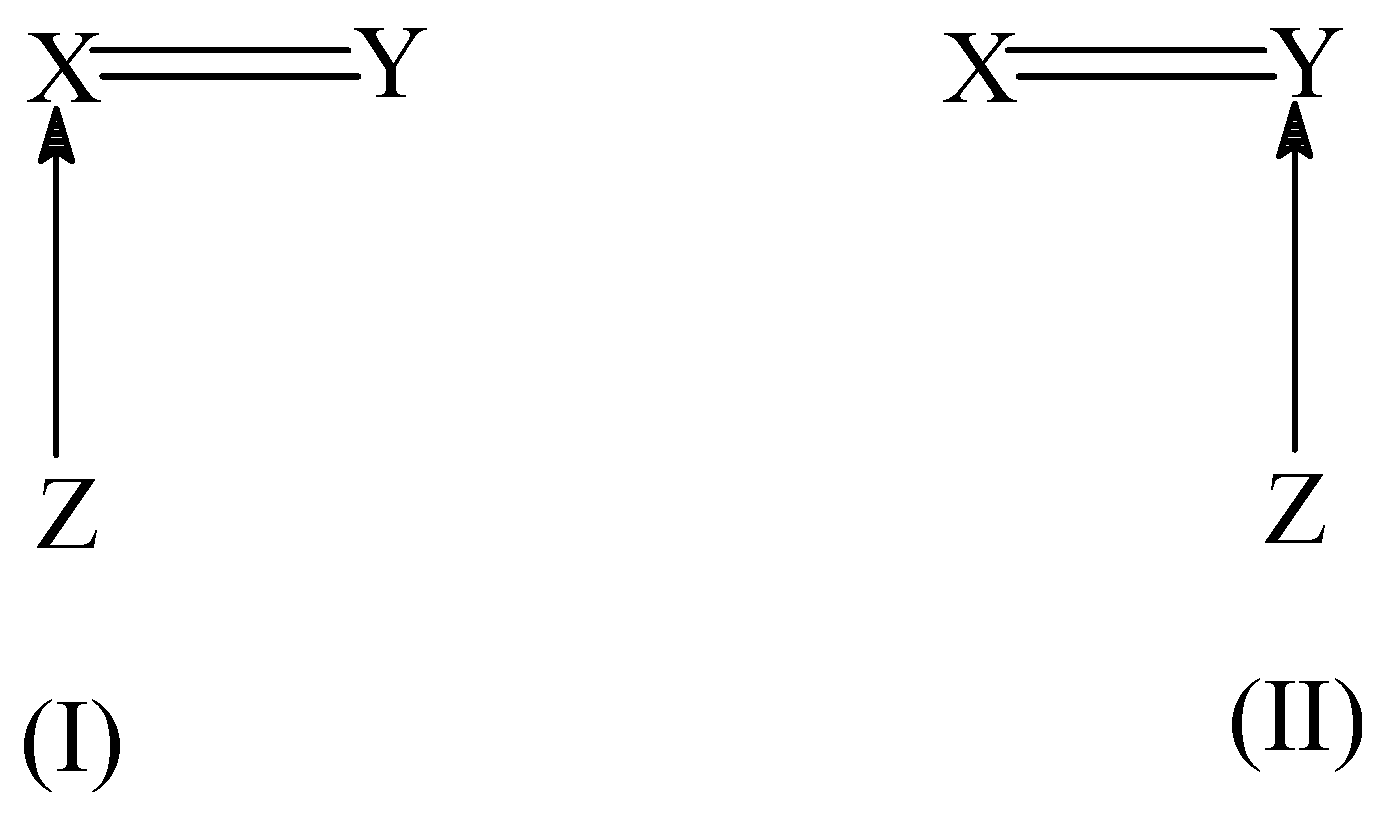1. Introduction
According to the density functional theory (DFT), the properties of a molecular system are determined by its total electron density [
1]. However, electron density alone could not describe all the chemical phenomena. Its sensitivities to structural perturbations and responses to the changes in external conditions are rather more important in reflecting the chemical reactivity of a system than its absolute values. Therefore much effort has recently been devoted to the development and application of reactivity indices derived from electron density.
Many of the well known, empirical but important, chemical concepts such as the chemical potential (μ), electronegativity (χ), hardness (η), softness (S)… appear naturally within the framework of DFT [
1]. This not only provides them with a new status but also gives a rigorous way for estimating their actual values. In general, these quantities correspond to the linear responses of the electron density with respect to changes in external potential (v) and number of electrons (N). These global parameters help understanding the behavior of a system and lead to widely applicable and useful principles such as the principle of maximum hardness [
2].
In a more local approach, the parameters mentioned above also emerge as a useful tool for rationalizing, interpreting and predicting diverse aspects of chemical bonding and reaction mechanism. The mathematical formalism of these quantities has been well presented in recent papers [
3,
4,
5]. Their applications to concrete problems by different groups [
4,
5] have also been well documented. We would refer to the latter reviews [
3,
4,
5] for the abundant literature. In the present article, we rather intend to discuss the applicability of two of these reactivity indices, namely the Fukui function and the local softness, that are mutually related to each other, on some particular problems selected from our own contributions, and where it is relevant, we will mention the results obtained by other groups but without a detailed discussion.
2. Basic Concepts
The chemical potential, electronegativity, hardness and softness are defined as follows [
6]:
where E, N, and v are the energy, number of electrons and the external potential of the system. Due to the discontinuity of the energy E with respect to the variation of N, one generally makes a finite difference approximation to derive η and S:
where IE and EA represent the first vertical ionization energy and electron affinity of the system, respectively. The quantities defined in (1), (2) and (3) are all global molecular properties and give information about the general behavior of a reactive molecule. Theoretical justification of the well known hard and soft acids and bases (HSAB) principle [
7] has also been given using chemical potential and softness [
6,
8]. As an extension, size, charge and dipole polarizability (α) were also used for a hard and soft classification [
6,
9]. There have been in fact numerous analytical and numerical evidences that softness has a closer link with the latter properties, especially with polarizability [
10,
11,
12,
13]. It has been observed in many cases that softness is linearly related to the cube-root of polarizability, α
1/3. Conversely, hardness is inversely proportional to α
1/3. Such relationship lends a support for the use of these physical properties for qualitative characterization of the HSAB concept.
In order to understand reaction mechanism, however, apart from the global properties, we also need the local quantities that vary from place to place and could be used as a measure of reactivity of the different sites within a supermolecule. Local reactivity parameters are thus necessary for differentiating the reactive behavior of atoms forming a molecule. Fukui function (f) [14(a)], and local softness (s) [14(b)] are two of such local reactivity parameters that we have at hand.
The Fukui function f(r) and local softness s(r) are mutually related and can be written as follows [
14]:
and
In a way, Fukui function represents the response of the chemical potential of a system to a change in external potential and could thus be regarded as an important index of reactivity. Once again, due to the discontinuity of the electron density with respect to N, finite difference approximation leads to three types of Fukui function for a system [
14], namely f
+(r) for nucleophilic attack, f
-(r) for electrophilic attack, and f
o(r) for radical attack that are defined as follows:
In practice, however, a more convenient way of calculating the f(r) functions at atomic resolution is to use the condensed Fukui functions [
15]. The condensed form of Fukui functions for an atom k in a molecule are expressed as:
where q
k is the electronic population of atom k in the molecule under consideration. Perhaps the most useful and important application of local softness resides in the interpretation and thereby prediction of reaction mechanism, especially in rationalizing site-selectivity and/or regio-selectivity. It is known that atomic charges and frontier orbital theory (FMO) are generally used to probe the regio-selective nature of a reaction. Thus, DFT-based parameters that combine both charge and orbital information, could emerge as a novel and alternative approach to the site selectivity problem in chemical reactions.
4. Hydration of Cumulenes
A hydration reaction of a doubly bonded substrate usually involves a water oligomer (H
2O)
n which ranges up to a tetramer (n=4) [
19]. The hydration occurs by an initial
nucleophilic attack of one water oxygen to one site of the double bond, followed by a proton relay within the water chain and ended up by an
electrophilic attack of a proton to another site [
19,
20,
21,
22,
23].
As a cumulene molecule possesses two distinct double bonds (X=C=Y), the hydration could thus present a regioselectivity with water adding preferentially to one of the two available double bonds. We have considered the mechanism of hydration [
19,
20,
21,
22,
23] and similar alcololysis [
24] and amination [
25] reactions in several typical cumulenes such as isocyanates (R-C=N=O), ketenes (RRC=C=O), ketenimines (RRC=C=NR), carbodiimides (RN=C=NR), carbon dioxide (O=C=O) and carbon suboxide (O=C=C=C=O). The most interesting result for this type of addition is perhaps the finding that the most kinetically favored channel does not always lead to the most thermodynamically stable adduct. Formation of novel reaction intermediates, namely the less stable enols, was frequently predicted, and this theoretical prediction was finally verified by experimental evidence [
20,
21,
24,
25]. Moreover, such site selectivity could be understood in terms of Fukui functions f(r).
Let us consider a typical case involving the hydration of isocyanates (R-N=C=O + (H
2O)
n). The addition is characterized by two different transition structures in which the water moiety approaches either the C=N or the C=O bond (
Scheme 2). In terms of energy barriers, although the values obtained are dependent on the methods employed, the addition of water across the C=N double bond is calculated to be consistently favored over that across C=O, irrespective of the number of water molecules considered. Calculations of the local softness maps indicate that a
nucleophilic attack is likely occurs at the central carbon, whereas the nitrogen site is clearly favored over the oxygen for an
electrophilic attack, due to the more extended concentration of electron density. Thus, coherent with the calculated energy barriers of the two corresponding TS’s mentioned above, the favored addition is expected to proceed through an addition of a water oxygen (O) on the cumulene central carbon (C, having the largest f
+ value) whereas a proton transfer occurs at the terminal nitrogen (N, having the largest f
- value; cf.
Scheme 2, structure (A)). This shows the higher ability of nitrogen in isocyanates to accept and to distribute positive charge to gain stabilization even though the oxygen carries a larger formal negative charge (approach (B) in
Scheme 2). This corroborates the fact that isocyanates usually undergo an N-protonation. Predictions derived from local softnesses were also successful for the similar processes in ketenes, ketenimines and carbon suboxide [
21,
22,
23] that show a variety of regio-selectivities.
5. Regiochemistry in Cycloadditions of Isocyanides
Isocyanides usually react with a wide range of substrates, including
electrophiles,
nucleophiles and radicals giving rise to different imine adducts. The mechanism and especially the stereospecificity of these addition reactions have been an active area of research. In our group, we studied the [2+1] addition reactions between isocyanide and heteronuclear dipolarophiles X=Y (X = C, Si, P and Y=Si, P, N, O, S) [
26] and acetylenes R-C ≡ C-H [
27]. In these addition reactions, two distinct transition structures, as depicted in (I) and (II) of
Scheme 3, can be found corresponding to the initial attack of the isocyanide carbon atom to the two doubly bonded atoms in the dipolarophile. Quite often, both TS’s (I) and (II) have an energy difference ranging from 10 to 100 kJ/mol.
Such a predominance of one TS over the other introduces a clear-cut regiospecificity in the addition reaction. This observed selectivity in the initial attack was explained by using the condensed-to-atom softness. Since the isocyanide HNC behaves as a
nucleophile in these addition reactions, the most
electrophilic center of the dipolarophile should be the preferred site for HNC attack. The local softness values for
nucleophilic attack (s
+) were calculated for the two atoms (X and Y) in the dipolarophile and it was found that in almost all the cases the preferred site of attack (marked by * in the
Table 2) has larger softness than the other atom. This clearly explains the observed site-selectivity in these addition reactions. More recently, the addition reactions between isocyanide and substituted acetylenes were studied in which isocyanide was found to behave as an
electrophile. The observed site-selectivity in these addition reactions was explained from the local softness values for
electrophilic attack (s
-) for the two carbon atoms of substituted acetylene. Local softness is also found to be successful in explaining the site-selectivity in adsorption of different base molecules such as CO, NH
3 on zeolite surfaces [
28,
29].
6. Pericyclic additions viewed from the local hard soft acid base (HSAB) principle
Local softness has also been applied successfully for explaining the regiochemistry in a more complex pericyclic addition reactions. For example, 1,3-dipolar cycloaddition reactions between various dipoles and dipolarophiles [
30,
31,
32], excited state cycloadditions [
33], and [4+2] Diels-Alder reactions [
34] were studied recently by using local reactivity descriptors. However, in order to explain the regiochemistry of a multicenter reaction, such as cycloaddition, apart from the local softness one also needs to consider HSAB principle in a local sense.
Let us consider the interaction energy between two chemical species A and B, the one is electrophilic and the other nucleophilic. From a global point of view and in neglecting the effect of change in external potential of A and B, the change in grand potential can be expressed as [
35]:
Table 2.
Global softness, condensed Fukui function and softness for nucleophilic attack for various dipolarophiles. The calculations were performed by using B3LYP/6-31G(d,p) method. Fukui function values were estimated from electrostatic potential (ESP) derived atomic populations.
Table 2.
Global softness, condensed Fukui function and softness for nucleophilic attack for various dipolarophiles. The calculations were performed by using B3LYP/6-31G(d,p) method. Fukui function values were estimated from electrostatic potential (ESP) derived atomic populations.
| Molecule | S | Atoma) | f+ | s+ |
| H2C=SiH2 | 2.73 | C | -0.11 | -0.31 |
| Si* | 0.84 | 2.31 |
| H2C=PH | 2.49 | C* | 0.16 | 0.41 |
| P | 0.69 | 1.72 |
| H2C=NH | 2.05 | C* | 0.49 | 1.00 |
| N | 0.27 | 0.56 |
| H2C=O | 2.12 | C* | 0.61 | 1.30 |
| O | 0.21 | 0.45 |
| H2Si=PH | 3.07 | Si* | 0.50 | 1.55 |
| P | 0.44 | 1.36 |
| H2Si=NH | 2.56 | Si* | 0.85 | 2.16 |
| N | 0.08 | 0.22 |
| H2Si=O | 2.48 | Si* | 0.94 | 2.34 |
| O | 0.04 | 0.10 |
| H2Si=S | 3.04 | Si* | 0.70 | 2.13 |
| S | 0.30 | 0.91 |
| HP=O | 2.79 | P* | 0.80 | 2.22 |
| O | 0.13 | 0.36 |
| HP=S | 3.44 | P* | 0.53 | 1.83 |
| S | 0.42 | 1.44 |
| HNC | 1.69 | C | 1.11b) | 1.88b) |
In order to prove the HSAB principle, it have been shown [
35] that for a given chemical potential difference μ
A − μ
B and a given S
B, the minimisation of ΔΩ
A with respect to S
A leads precisely to S
A = S
B. At the same time the minimisation of ΔΩ
B with respect to S
B at fixed μ
B − μ
A and S
A leads to S
B = S
A. Under these conditions (ΔΩ
A)
min = (ΔΩ
B)
min. Basically, it implies that the grand potential of all the atoms in A and B becomes a minimum when A and B have an approximately equal global softness.
An extension of the above idea to the atomic level [
36] showed that when two molecules A and B form a new molecule AB, then the change in electronic population for each atom in A (say k) and B (say l), can be written as:
While the change in grand potential can be expressed as [
36],
Now, if the interaction between A and B occurs through the kth atom of A and lth atom of B, then it is reasonable to assume that most favourable situation corresponds to (ΔΩ
Ak)
min = (ΔΩ
Bl)
min, and which finally leads to s
Ak = s
Bl. Thus, the interaction between A and B is favored when it occurs through those atoms whose softnesses are approximately equal: that is essentially the local HSAB principle [
36].
The combination of local softness and local HSAB principle can be useful for the interpretation of regiochemistry in many cycloaddition reactions as demonstrated below in some representative examples.
In our group, intensive attempts have been made to apply local softness for the interpretation of the observed regiochemistry in various cycloaddition reactions between a 1,3-dipole (C=D=E, henceforth referred to as 13DP) and a dipolarophile (A=B, hereafter referred to as DPh) [
31,
37]. These 1,3-dipolar cycloaddition (13DC) reactions are important in synthetic organic chemistry due to the potential of forming many starting materials for the syntheses of heterocycles. The problem of primary importance here concerns the regiochemistry of the cycloaddition. When a dipolarophile A=B and a 1,3-dipole C=D=E approach to each other, two cycloadducts are, in principle, possible (cf.
Scheme 4):
In a majority of the cases considered, however, one transition state structure is calculated to be lower in energy than the other, and thus the reaction proceeds mainly through the lower energy transition state. Again, this introduces a regioselectivity in addition [
38,
39,
40,
41,
42]. For example, in the case of cycloaddition between HCP and H
2CNN, the transition state where C-atom of H
2CNN forms a bond with the P-atom of HCP is lower in energy and the reaction proceeds mainly through this TS [
39].
Although the local HSAB principle states that in addition reactions the two atoms with closer softness should join together, but in a multicenter addition reaction, simultaneous fulfillment of local HSAB principle at all the termini is important. One thus needs to define a quantity that can be used as a measure of fulfillment of HSAB principle. To this end, the following expressions were proposed [
33,
34], which measure the fulfillment of HSAB principle in a least square sense for both the termini involved in cycloaddition (see
Scheme 4).
The
and
are the softness values for
electrophilic attack for the two atoms of 13DP involved in cycloaddition (see
Scheme 4, whereas the
and
are the softness for
nucleophilic attack for the two atoms of DPh participating in the 13DC. Here, 13DP and DPh are considered, respectively, as
nucleophile and
electrophile. However, in the opposite case when 13DP and DPh behave as
electrophile and
nucleophile, respectively, the signs in the superscripts of the above expressions should be the reverse. The smaller the value of Δ the greater is the extent that the HSAB principle is satisfied. The product associated with reaction channel having smaller Δ value is thus expected to be the predominant product. Recently, a more general theoretical justification for using the expression (15) as a criteria to regio-selectivity in cycloadditions [
43].
The same approach was adopted [
33] for explaining the regiochemistry in excited state [2+2] photocycloaddition reactions of carbonyls with several partners containing a double bond. Such as in 13DC, two modes of addition exist for these excited state cycloaddition reactions. However, it was observed [
33] that one photocycloadduct is always predominate over the other, which thus introduces a regioselectivity in the addition reactions. The Δ values associated with two modes of addition were calculated from the atomic softness values and using equation (15). It was observed that the reaction channel forming the predominant product is always associated with a smaller Δ value [
33]. Thus the product formed by maintaining the HSAB principle is invariably the major product observed in the photocycloaddition reaction.
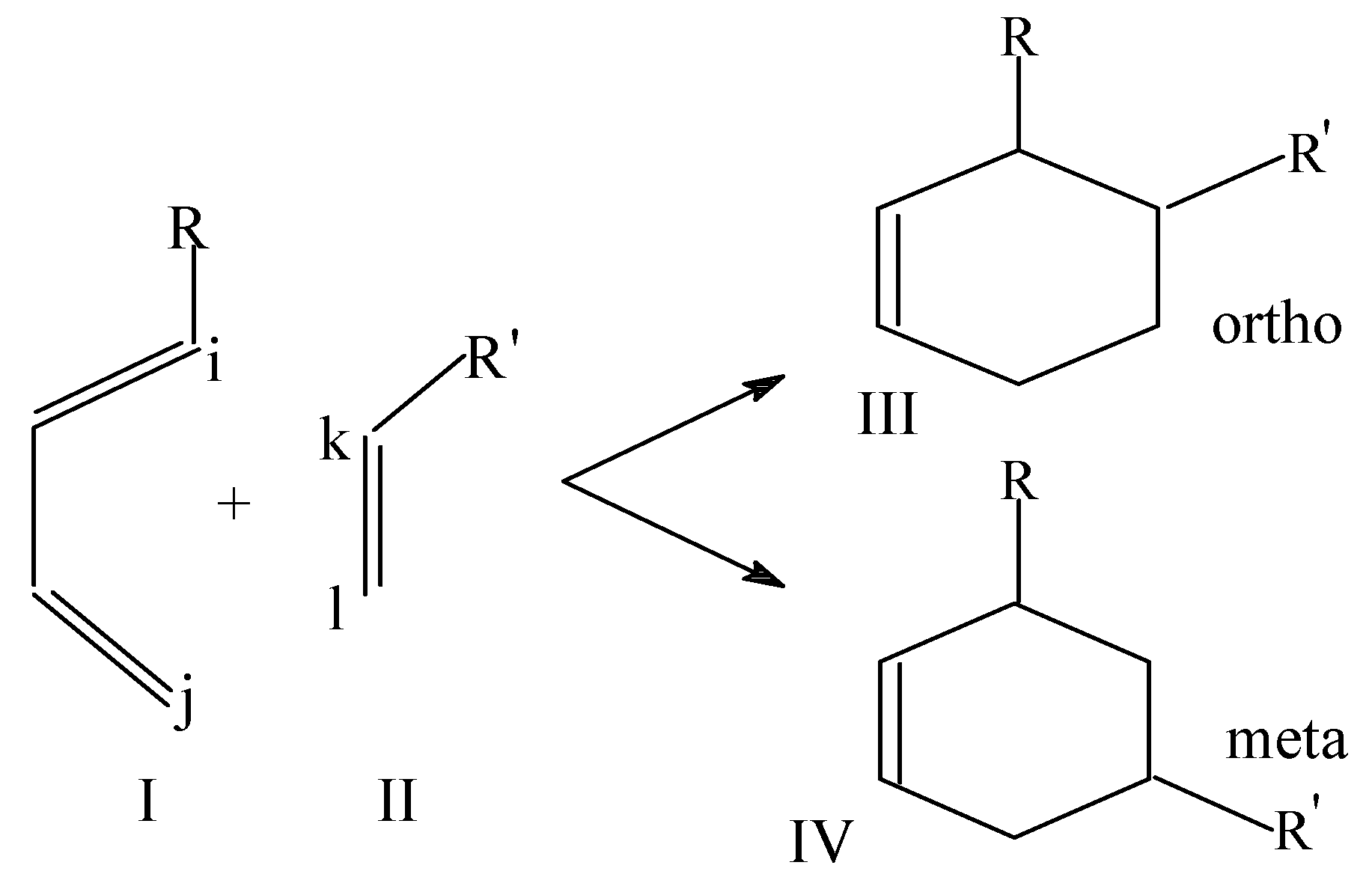
Local softness and HSAB principle have also been used as a regioselectivity indicator in Diels-Alder reactions between diene and dienophile [
34]. It is well known that in these [4+2] cycloaddition reactions one of the two possible regio-isomers (structure III in
Scheme 5) predominates over the other:
The values of Δ for both the modes of addition were calculated from the following expressions by using the atomic softness values estimated:
Diene acts as nucleophile and dienophile as an electrophile in these reactions. As discussed earlier, the product associated with a smaller Δ value is expected to be the predominant product. Taking different R and R', 48 Diels-Alder reactions have been studied and it is observed that in all the reactions but with R and R'=CN, Δ
ortho < Δ
meta [
34]. Thus the product formed by maintaining the HSAB principle is found to be the predominant product in the Diels-Alder reactions between dienes and dienophiles.
All the examples discussed above show that the regiochemistry in diverse chemical reactions can be explained by combining local softness and local HSAB principle. In view of the simplicity of this approach, the success is truly remarkable. It is also important to note that all the predictions are made from isolated molecular properties only. Thus some odd cases may eventually appear when perturbations, due to the presence of the other molecule, are significant or some other stronger factors exist, such as stereoelectronic effect or nuclear repulsion. However, it was observed in the context of 13DC reactions that the regioselective behavior predicted from the model based on local softness values for the isolated molecules remain unchanged even after the inclusion of polarization and charge transfer effects on local softness.