Time Dependent Coupled Cluster Approach to Resonance Raman Excitation Profiles from General Anharmonic Surfaces
Abstract
:Introduction
Theory
Preliminary remarks:
Vibrational states of the ground surface:
Time propagation :
Results and discussion
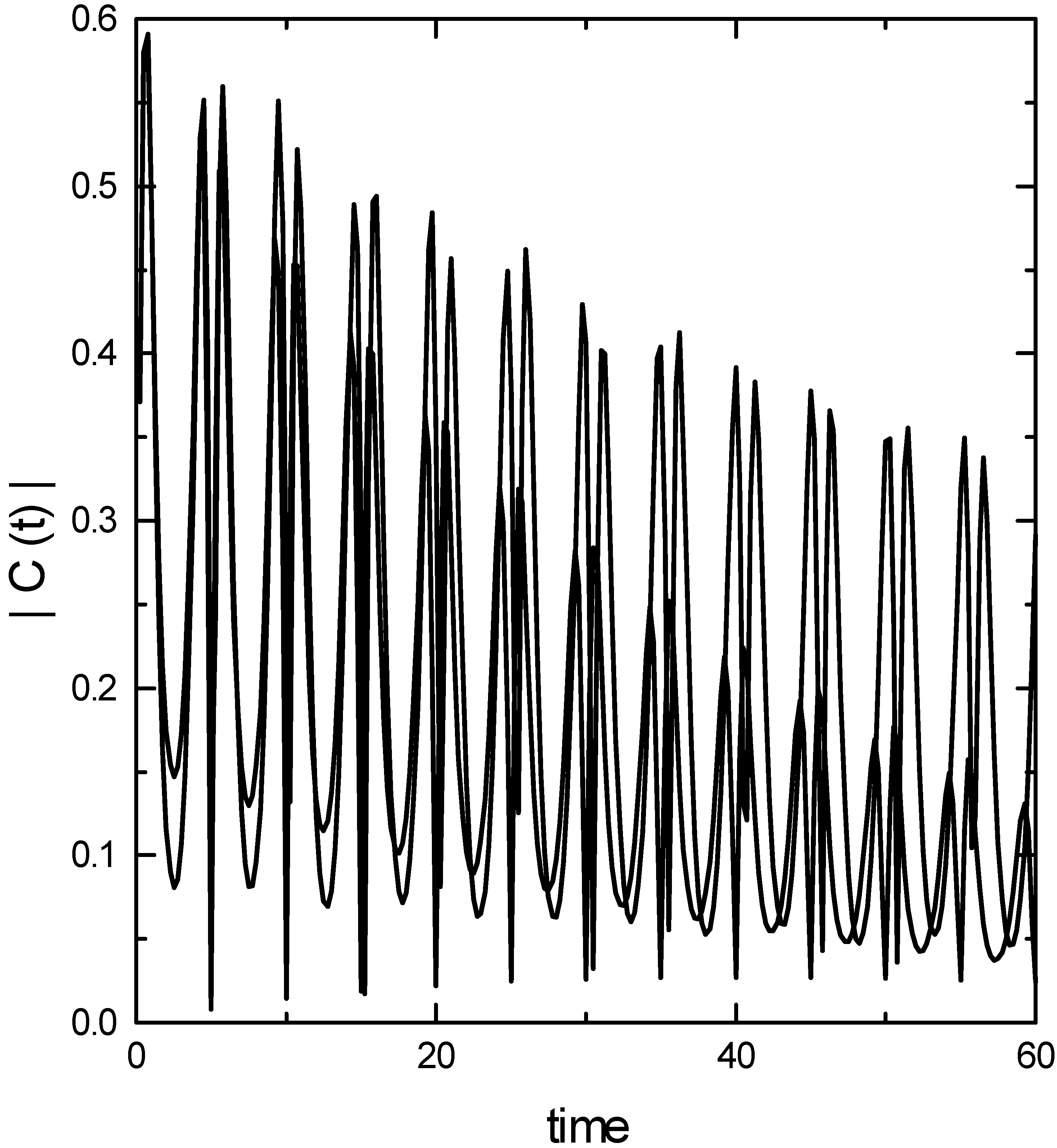
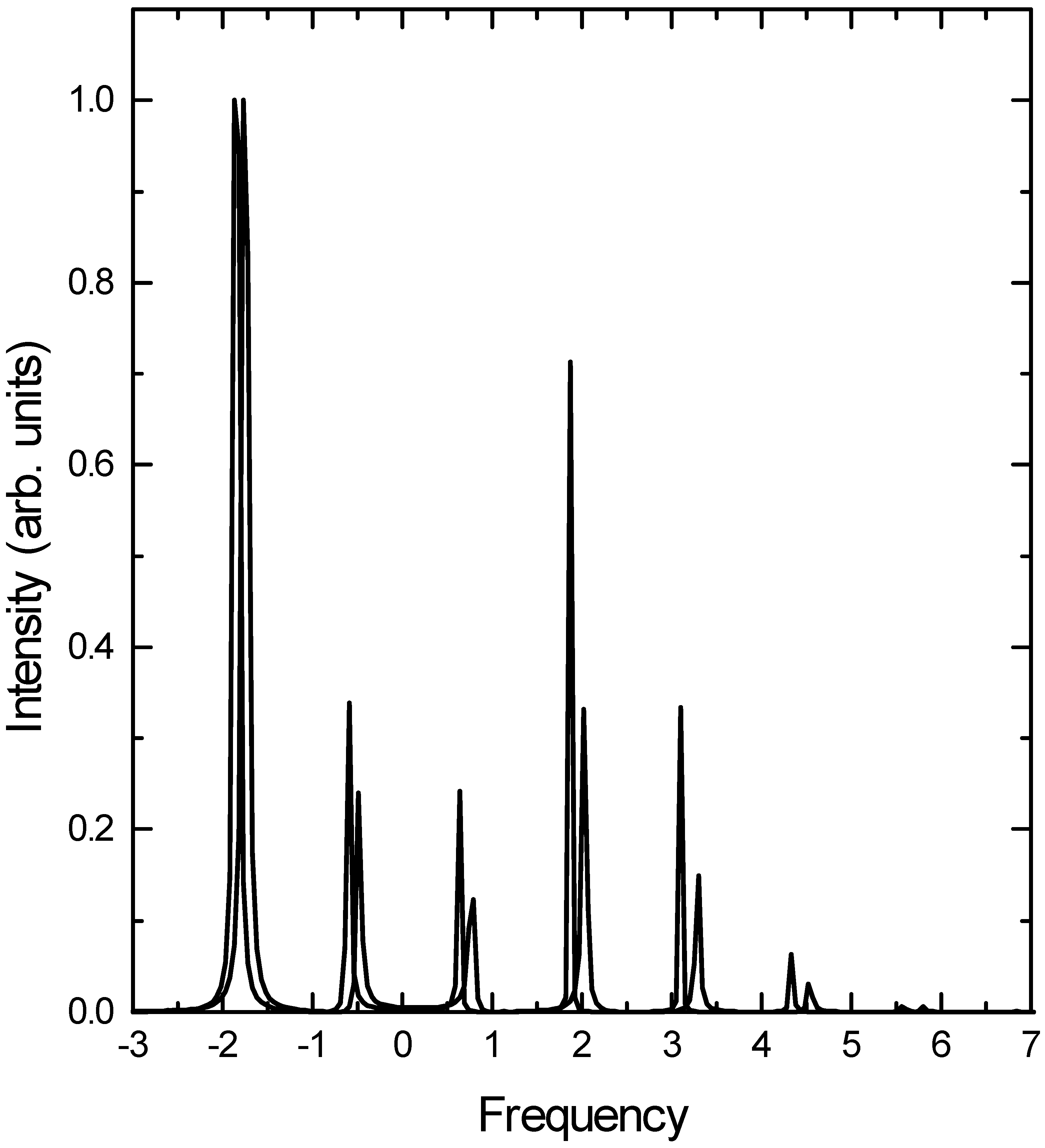

Acknowledgements
References
- Kramers, H.A.; Heisenberg, W. Z. Phys. 1925, 31, 681.Dirac, P. Proc. R. Soc., London 1927, 114, 710. [CrossRef]
- Lee, S.-Y.; Heller, E.J. J. Chem. Phys. 1979, 71, 4777.
- Tanner, D. J.; Heller, E.J. J. Chem. Phys. 1985, 82, 1982.
- Heller, E.J. Acc. Chem. Res. 1981, 14, 368. [CrossRef]
- Friesner, R.; Pettitt, M.; Jean, J.M. J. Chem. Phys. 1985, 82, 2918. [CrossRef]
- Coalson, R.D.; Kinsey, J.L. J. Chem. Phys. 1986, 85, 4322.
- Page, B.; Tonks, D.L. J. Chem. Phys. 1988, 88, 738.
- Gerdts, T.; Manthe, U. J. Chem. Phys. 1997, 107, 6584.
- Heller, E.J. J. Chem. Phys. 1978, 68, 2066.
- Cizek, J. Adv. Chem. Phys. 1969, 14, 35.
- Bartlett, R.J. Ann. Rev. Phys. Chem 1981, 32, 359.
- Mukherjee, D.; Pal, S. Adv. Quantum Chem. 1988, 20, 291.
- Lindgren, I.; Mukherjee, D. Phys. Rept. 1987, 151, 93. [CrossRef]
- Bartlett, R.J. J. Phys. Chem., 93 1989, 93, 1697. [CrossRef]
- Nagalakshmi, V.; Lakshminarayana, V.; Sumitra, G.; Durga Prasad, M. Chem. Phys. Lett. 1994, 217, 279.
- Durga Prasad, M. Ind. J. Chem 2000, 39A, 196.
- Patwari, G.N.; Wagegaonkar, S.; Durga Prasad, M. Chem. Phys. Lett. 2001, 344, 229.
- Sreelatha, G.; Durga Prasad, M. J. Chem. Phys. 1996, 105, 2972.
- Durga Prasad, M. Theor. Chim. Acta 1994, 88, 383. [CrossRef]
- Durga Prasad, M. J. Chem. Phys. 1988, 88, 7005.
- Monkhorst, H. Int. J. Quantum Chem. 1977, S11, 421.Mukherjee, D.; Mukherjee, P.K. Chem. Phys. 1979, 37, 325.Emrich, K. Nucl. Phys. A. 1981, 351, 379.Koch, H.; Jorgenson, P. J. Chem. Phys 1990, 93, 3333. [CrossRef]Stanton, J.F.; Bartlett, R.J. J. Chem. Phys. 1993, 98, 7029.
- Sree Lath, G.; Durga Prasad, M. Theor. Chim. Acta. 1993, 86, 511. [CrossRef]
© 2002 by MDPI (http://www.mdpi.org).
Share and Cite
Prasad, M.D. Time Dependent Coupled Cluster Approach to Resonance Raman Excitation Profiles from General Anharmonic Surfaces. Int. J. Mol. Sci. 2002, 3, 447-458. https://0-doi-org.brum.beds.ac.uk/10.3390/i3050447
Prasad MD. Time Dependent Coupled Cluster Approach to Resonance Raman Excitation Profiles from General Anharmonic Surfaces. International Journal of Molecular Sciences. 2002; 3(5):447-458. https://0-doi-org.brum.beds.ac.uk/10.3390/i3050447
Chicago/Turabian StylePrasad, M. Durga. 2002. "Time Dependent Coupled Cluster Approach to Resonance Raman Excitation Profiles from General Anharmonic Surfaces" International Journal of Molecular Sciences 3, no. 5: 447-458. https://0-doi-org.brum.beds.ac.uk/10.3390/i3050447



