Introduction
The reactions of azo coupling of aromatic amines and phenols with the aryldiazonium cations are of great importance in dyes production [
1,
2], in analytical chemistry [
3]. The participants (amines, phenols) and products (azo compounds) of the above reactions are priority toxicants of the environment. The diazotization and azo coupling reactions are very important for the NO
2− [
3] and N-nitrosamines determination. Nitrite ion is eco toxicant and priority environmental pollutant, precursor of N-nitrosamines possessing carcinogenic and mutagenic effects. Nitrites are added to meat products to render a market appearance. Actual is the problem of analytical determination of nitrites in foods. Thus a demand emerges for the diazonia reactivity
a priori predictions.
Diazonium cations may be chemically and electrochemically reduced [
4,
5,
6,
7,
8,
9,
10,
11]. For many substances, capabilities of being exposed to electrophilic (nucleophilic) attack and undergoing oxidation (reduction) change with symbate character [
12,
13,
14,
15]. So a tendency of diazo cations for reduction could be a measure of their electrophilic activity on azo coupling. For establishing an optimal rate of azo dyes formation reactions, appropriate is
a priori prediction of reduction potentials and electron affinities for diazonium cations of a given structure followed by their directive synthesis.
Diazonium cations are capable of decomposing to form nitrogen molecules [
2,
9,
11,
16]. In order to provide the high dyes yields, satisfactory correctness, reproducibility and other metrological characteristics of analytical techniques, it is desirable to eliminate the above competing reaction, to evaluate quantitatively an extent of decomposition of newly synthesized diazonium salts.
A measure of diazonium cations stability (and at the same time an indicator of their activity as electrophilic agents) can be, in particular, frequencies of stretching vibrations of the atomic group C-N
+≡N bonds [
16,
17,
18,
19,
20,
21].
Direct correct computation of vibrational frequencies is very complicated problem requiring the
ab initio approach. Therewith the Hartree-Fock method dramatically (for 200-500 cm
−1) overestimates the high frequencies (≥ 1600 cm
−1), considerably underestimates low ones (≤ 300 cm
−1) and systematically (for 100-200 cm
−1) overestimates the rest ones because of non-allowance for electron correlation [
22,
23]. The latter, even being considered within the framework of MP2 theory, does not contribute to the better situation. The DFT (B3LYP) method is much more successful in simulating the aforesaid values: high frequencies (≥ 1600 cm
−1) overestimation consists 100-150 cm
−1, low frequencies (≤ 300 cm
−1) are underestimated to the lesser extent, and moderate ones (300-1600 cm
−1) are 20-50 cm
−1 overestimated. However, hybride character of DFT (presence of a semiempirical component) in a number of cases leads to great errors for low frequencies (≤ 500 cm
−1) and to the non-predictible asymptotic behaviour of adiabatic potential at long internuclear distances [
24]. For poor-symmetry molecules, the frequencies computation is severely complicated by the unharmonic disturbances as those of Fermi resonance type, by the presence of composed frequencies, decreased number of experimental criteria of assignment. Besides, on the difference between vibrational levels energies comparable to the quantum chemical method error (20-50 cm
−1 with respect to DFT), accident coincidence between the computed and experimental frequencies is possible. Therefore it is of value to have simple (established on the basis of semiempirical quantum chemical computations) quantitative interrelations for estimating the vibrational spectra frequencies.
In general, for rather simplified obtaining quantitative relations for the predicting of different physicochemical properties, the semiempirical quantum chemical methods would be reasonable to use.
As will be shown below, vibrational frequencies and electron affinities correlate with the mesomeric dipole moments of substituents in the aryldiazonium cations.
The aim of the present work is finding (on the basis of quantum chemical computations) the quantitative structure - property relationships in order to predict the reduction potentials and some related quantities, electron affinities, stretching vibrational frequencies for fragment C-N+≡N bonds in aryldiazonium cations, mesomeric dipole moments of atomic groups.
Computational Methods
The computations were performed by means of the PM3 method [
25,
26] using the software from the
MOPAC package [
27,
28] with the complete geometry optimization (Broyden-Fletcher-Goldfarb-Shanno function minimizer) [
29] involving Thiel's fast minimization algorithm [
30]. The preliminary optimization was realized by the molecular mechanics method (the MMX procedure) [
31] with the software of the
PCMODEL complex [
31]. In quantum chemical computations, the condition of the gradient norm not exceeding 0.02 kcal/(mol
.Å) was preset. In some cases, the sufficient decrease in gradient norm was achieved by means of abandonment of the Thiel's fast minimization routine (the key word NOTHIEL of the
MOPAC package was applied), or under optimization with the Davidon - Fletcher - Powell method (key word DFP) [
29], or by conducting double precision calculations (key word PRECISE), as well as using combined approaches involving the key words NOTHIEL, DFP and PRECISE.
For molecules with closed electronic shells, the computations were carried out within the restricted Hartree - Fock (RHF) formalism [
28]. For the radicals formed at the diazonium salts reduction, the unrestricted Hartree - Fock (UHF) method [
28] was used.
In calculating the rotational contributions to thermodynamic functions the symmetry number was taken as unity.
The linear regression analysis was performed with the confidence level of 0.95 taking into account the Student coefficient.
Results and Discussion
Aryldiazonia XC6H4N+≡N with X = H, 2-CH3, 3-CH3, 4-CH3, 2-CF3, 3-CF3, 4-CF3, 4-CCl3, 4-CN, 4-COCH3, 4-COC6H5, 2-COOCH3, 3-COOCH3, 4-COOCH3, 2-COOC2H5, 4-COOC2H5, 4-NH2, 4-NHCH3, 4-N(CH3)2, 4-N(C2H5)2, 4-NHCOCH3, 2-NO2, 3-NO2, 4-NO2, 2-OH, 3-OH, 4-OH, 2-OCH3, 3-OCH3, 4-OCH3, 3-F, 4-F, 4-Si(CH3)3, 4-SiCl3, 4-SH, 4-SCH3, 4-SO2CF3, 4-SO2NH2, 2-Cl, 3-Cl, 4-Cl, 3-Br, 4-Br, 4-I have been considered in this work.
For the series of compounds, earlier we have established a correctness of the most important thermodynamic and molecular characteristics reproduction by the MNDO, AM1 and PM3 methods [
32,
33,
34,
35,
36,
37,
38,
39,
40,
41,
42,
43], as well as of electronegativity, inductive and mesomeric parameters of atomic groups [
44]. Among the mentioned methods PM3 seems to provide satisfactory results in obtaining the heats of formation for nitro derivatives [
26,
32] and dimethylsulphone [
34]. Some of the molecular systems under study contain NO
2 or SO
2 group. That is the reason for selecting the PM3 [
25,
26] method for the purposes of this work.
The PM3 method is suitable for quantitative structure - property relationships establishment for series of similar electroneutral or charged species within which possible errors compensate each other due to the fundamental relativistic principle. So it is quite correct to apply the PM3 directly, and there is no necessity to bridge the quantum chemical computations to the molecular mechanics ones, as well as to use ab initio, ECP, DFT or some other more sophisticated approach.
The standard free energy ΔG
f values were calculated from the relationship:
where the standard entropies of formation ΔS
f were calculated by the formula:
in which S
i are the entropies of the elements constituting molecule in their standard states [
45] in view of hydrogen, nitrogen, oxygen, fluorine, rhombic sulphur, chlorine, bromine, iodine being the two-atomic molecules; T = 298.15 K.
In our work, the standard heats of formation ΔHf and standard entropies S were generated directly by the MOPAC package.
Of importance is to explain how the S values were computed. The contributions of separate degrees of freedom for translation, rotation and vibration motions to entropy were computed in the rigid molecule approximation (barriers of rotation and inversion far exceed kT) with no allowance for vibrations anharmonicity. The translation contributions were calculated without using quantum chemical computations, and the rotation contributions relying on the data on equilibrium internuclear distances obtained in the course of quantum chemical treatment. Finally, the contributions of vibration components of entropy were evaluated on the basis of normal vibrations frequencies computed by the quantum chemical method. For computing the frequencies after geometry optimization, second-order derivatives of total energy by natural coordinates (force constants) were preliminary computed [
46].
Interrelationship of reduction potentials and some related quantities with electron affinities
Polarographic reduction half-wave potentials (E) depend linearly on the energies of lowest unoccupied molecular orbitals of depolarizers [
47] and, thus, in accordance with Koopmans theorem [
48], on their electron affinities (A). It would be reasonable to assume the analogous relationship between the chemical reduction potentials and A.
From the viewpoint of finding the quantitative structure - property relationships in the series of diazonium cations, the reverse problem is also of interest, namely the electron affinities evaluation using the measured reduction potentials. Electron affinity is one of the most important and, at the same time, hard-to-get characteristics of electronic structure, molecules capability of electron-accepting and being reduced.
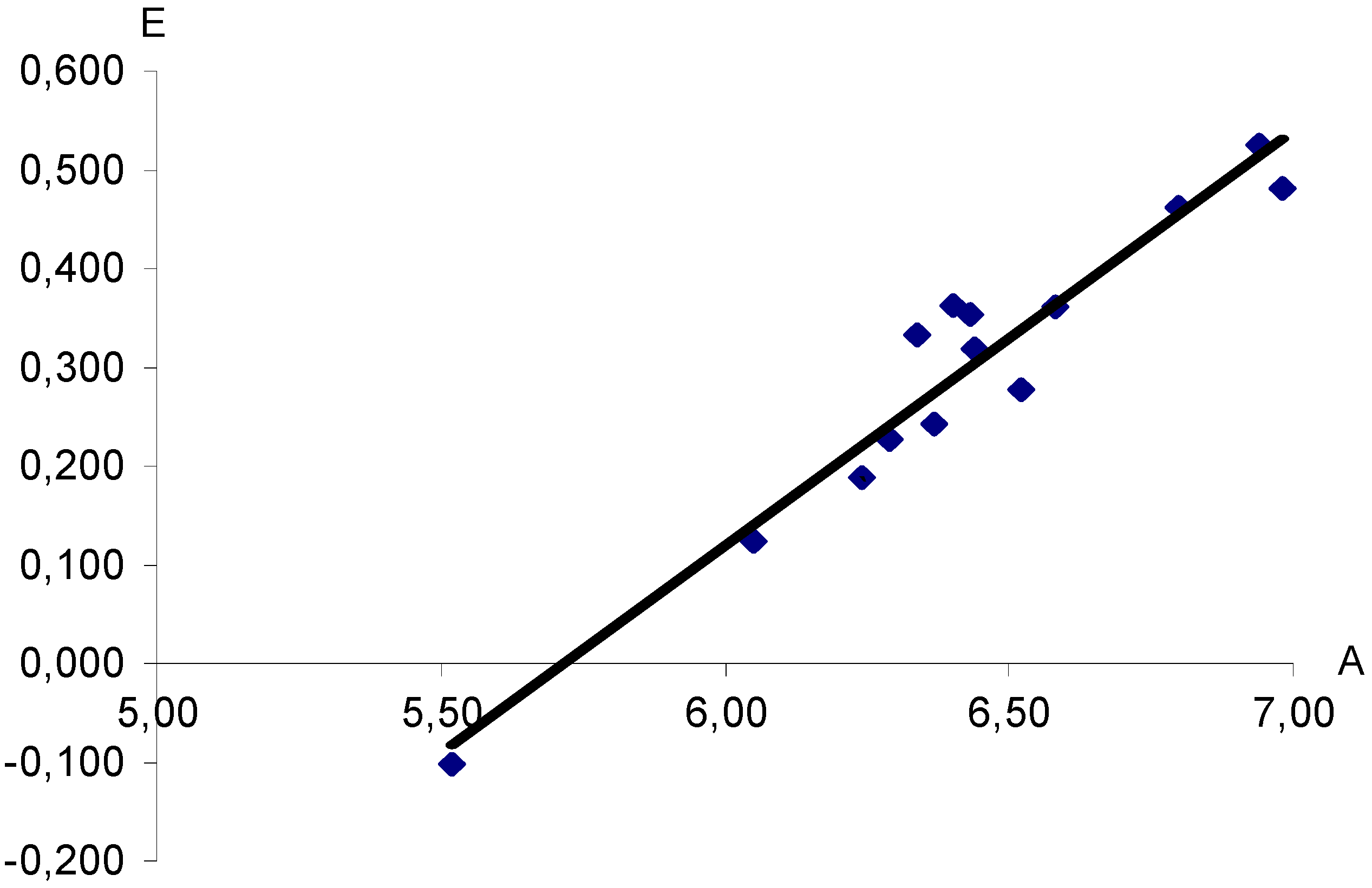
We have established the linear dependences of E
vs A and A
vs E, where E are redox potentials or polarographic reduction potentials, A are Koopmans electron affinities (see two dependences below, along with
Figure 1 and
Table 1a and
Table 1b). The following designations are accepted: m is the number of considered points, r is the correlation coefficient.
Given are interrelationships of half-wave potentials (E) of polarographic reduction of aryldiazonium XC
6H
4N
+≡N (X = H, 2-CH
3, 3-CH
3, 4-CH
3, 4-CN, 4-N(CH
3)
2, 2-OCH
3, 4-OCH
3, 2-Cl, 3-Cl, 4-Cl, 3-Br, 4-Br, 4-I) tetrafluoroborates in sulfolane [
4,
9] measured
vs. saturated Hg
2Cl
2 electrode, and proton affinities (A) (m = 14; e is the electron charge):
Figure 1.
Dependence of half-wave potentials (E, V) of polarographic reduction of aryldiazonium XC6H4N+≡N cations (measured in nitromethane vs saturated Hg2Cl2 electrode) upon computed proton affinities (A, eV). X = H, 3-CH3, 4-CH3, 4-N(CH3)2, 3-NO2, 4-NO2, 4-OCH3, 3-F, 4-F, 4-SO2CF3, 3-Cl, 4-Cl, 3-Br, 4-Br. Correlation coefficient r = 0.9662.
Figure 1.
Dependence of half-wave potentials (E, V) of polarographic reduction of aryldiazonium XC6H4N+≡N cations (measured in nitromethane vs saturated Hg2Cl2 electrode) upon computed proton affinities (A, eV). X = H, 3-CH3, 4-CH3, 4-N(CH3)2, 3-NO2, 4-NO2, 4-OCH3, 3-F, 4-F, 4-SO2CF3, 3-Cl, 4-Cl, 3-Br, 4-Br. Correlation coefficient r = 0.9662.
Table 1a.
Correlations of redox-potentials
* (E) obtained on XC
6H
4N
+≡N cations titration, potentials of polarographic reduction (E) (
vs saturated Hg
2Cl
2 electrode) [
5,
6,
7,
11], with proton affinities (A)
Table 1a.
Correlations of redox-potentials* (E) obtained on XC6H4N+≡N cations titration, potentials of polarographic reduction (E) (vs saturated Hg2Cl2 electrode) [5,6,7,11], with proton affinities (A)
| Reduction mode | Set of substituents X | m | f, V** | g, e−1** | r |
| 1 | H, 3-NO2, 4-NO2, 3-Cl, 4-Cl | 5 | -1.921 ± 0.549 | 0.3561 ± 0.0835 | 0.9920 |
| 2 | H, 4-NO2, 3-Cl, 4-Cl | 4 | -2.775 ± 1.050 | 0.4908 ± 0.1609 | 0.9942 |
| 3 | 3-NO2, 4-NO2, 4-SO2CF3, 3-Cl, 4-Cl, 3-Br, 4-I | 7 | -0.9757 ± 0.6224 | 0.2075 ± 0.0940 | 0.9304 |
| 4 | H, 4-CH3, 4-N(CH3)2, 3-NO2, 4-NO2, 4-OCH3, 4-SO2CF3, 3-Cl, 4-Cl, 3-Br, 4-Br | 11 | -2.338 ± 0.578 | 0.4138 ± 0.0901 | 0.9607 |
| 5 | 3-NO2, 4-NO2, 4-OCH3, 4-SO2CF3, 3-Cl, 3-Br | 6 | -2.130 ± 0.794 | 0.3774 ± 0.1216 | 0.9741 |
| 6 | H, 4-N(CH3)2, 3-NO2, 4-NO2, 3-Cl, 4-Cl, 4-Br | 7 | -2.351 ± 0.665 | 0.4124 ± 0.1037 | 0.9769 |
| 7 | H, 3-CH3, 4-CH3, 4-N(CH3)2, 3-NO2, 4-NO2, 4-OCH3, 3-F, 4-F, 4-SO2CF3, 3-Cl, 4-Cl,3-Br, 4-Br | 14 | -2.398 ± 0.453 | 0.4198 ± 0.0704 | 0.9662 |
| 8 | H, 3-CH3, 4-CH3, 4-N(CH3)2, 3-NO2, 4-NO2, 4-OCH3, 3-F, 4-F, 3-Cl, 4-Cl, 3-Br, 4-Br | 13 | -2.431 ± 0.644 | 0.4222 ± 0.1008 | 0.9410 |
| 9 | H, 4-CH3, 4-N(CH3)2, 4-OCH3, 4-Cl, 3-Br, 4-Br | 7 | -2.446 ± 0.722 | 0.4272 ± 0.1164 | 0.9730 |
Table 1b.
Correlations of proton affinities (A) with redox-potentials
* (E) obtained on XC
6H
4N
+≡N cations titration and with potentials of polarographic reduction (E) (
vs saturated Hg
2Cl
2 electrode) [
5,
6,
7,
11]
Table 1b.
Correlations of proton affinities (A) with redox-potentials* (E) obtained on XC6H4N+≡N cations titration and with potentials of polarographic reduction (E) (vs saturated Hg2Cl2 electrode) [5,6,7,11]
| Reduction mode | Set of substituents X | m | h, eV** | i, e** | r |
| 1 | H, 3-NO2, 4-NO2, 3-Cl, 4-Cl | 5 | 5.413 ± 0.279 | 2.763 ± 0.648 | 0.9920 |
| 2 | H, 4-NO2, 3-Cl, 4-Cl | 4 | 5.664 ± 0.293 | 2.014 ± 0.660 | 0.9942 |
| 3 | 3-NO2, 4-NO2, 4-SO2CF3, 3-Cl, 4-Cl, 3-Br, 4-I | 7 | 4.959 ± 0.759 | 4.171 ± 1.889 | 0.9304 |
| 4 | H, 4-CH3, 4-N(CH3)2, 3-NO2, 4-NO2, 4-OCH3, 4-SO2CF3, 3-Cl, 4-Cl, 3-Br, 4-Br | 11 | 5.708 ± 0.173 | 2.231 ± 0.486 | 0.9607 |
| 5 | 3-NO2, 4-NO2, 4-OCH3, 4-SO2CF3, 3-Cl, 3-Br | 6 | 5.688 ± 0.308 | 2.514 ± 0.810 | 0.9741 |
| 6 | H, 4-N(CH3)2, 3-NO2, 4-NO2, 3-Cl, 4-Cl, 4-Br | 7 | 5.732 ± 0.199 | 2.314 ± 0.582 | 0.9769 |
| 7 | H, 3-CH3, 4-CH3, 4-N(CH3)2, 3-NO2, 4-NO2, 4-OCH3, 3-F, 4-F, 4-SO2CF3, 3-Cl, 4-Cl,3-Br, 4-Br | 14 | 5.759 ± 0.125 | 2.224 ± 0.373 | 0.9662 |
| 8 | H, 3-CH3, 4-CH3, 4-N(CH3)2, 3-NO2, 4-NO2, 4-OCH3, 3-F, 4-F, 3-Cl, 4-Cl, 3-Br, 4-Br | 13 | 5.830 ± 0.151 | 2.097 ± 0.501 | 0.9410 |
| 9 | H, 4-CH3, 4-N(CH3)2, 4-OCH3, 4-Cl,3-Br, 4-Br | 7 | 5.752 ± 0.145 | 2.216 ± 0.604 | 0.9730 |
One-electron reduction of diazonium cations leads to the formation of radicals [
7,
8,
9,
10] capable of undergoing dimerization [
7,
8,
10]:
Basing on the results of polarographic and potentiometric studies of aryldiazonium cations complicated by dimerization [
7,
8,
10], we have obtained the relationships combining the standard one-electron E
R0 and dimerization E
RR0 potentials, as well as the half-equivalent point potentials E
1/2 obtained on diazonia titration (
Table 1c,
Table 1d,
Table 1e and
Table 1f).
Table 1c.
Correlations of standard potentials of reductive dimerization (E
RR0), semineutralization potentials (E
1/2) (
vs saturated Hg
2Cl
2 electrode) obtained on XC
6H
4N
+≡N cations titration by sodium sulphite [
7,
8], with A values (m = 7)
*.
Table 1c.
Correlations of standard potentials of reductive dimerization (ERR0), semineutralization potentials (E1/2) (vs saturated Hg2Cl2 electrode) obtained on XC6H4N+≡N cations titration by sodium sulphite [7,8], with A values (m = 7)*.
| E | j, V** | k, e−1** | r |
| ERR0 | -1.864 ± 1.009 | 0.3381 ± 0.1543 | 0.9294 |
| E1/2 | -1.754 ± 1.135 | 0.3227 ± 0.1737 | 0.9057 |
Table 1d.
Correlations of A values with standard potentials of reductive dimerization (E
RR0) and with semineutralization potentials (E
1/2) (
vs saturated Hg
2Cl
2 electrode) obtained on XC
6H
4N
+≡N cations titration by sodium sulphite [
7,
8] (m = 7)
*.
Table 1d.
Correlations of A values with standard potentials of reductive dimerization (ERR0) and with semineutralization potentials (E1/2) (vs saturated Hg2Cl2 electrode) obtained on XC6H4N+≡N cations titration by sodium sulphite [7,8] (m = 7)*.
| E | l, eV** | n, e** | r |
| ERR0 | 5.653 ± 0.414 | 2.555 ± 1.166 | 0.9294 |
| E1/2 | 5.631 ± 0.499 | 2.542 ± 1.368 | 0.9057 |
Table 1e.
Correlations of E
R0, E
RR0, E
1/2 values (
vs saturated Hg
2Cl
2 electrode) obtained on XC
6H
4N
+≡N cations titration by sodium methylate in acetonitrile medium [
10], with A values (m = 6)
*
Table 1e.
Correlations of ER0, ERR0, E1/2 values (vs saturated Hg2Cl2 electrode) obtained on XC6H4N+≡N cations titration by sodium methylate in acetonitrile medium [10], with A values (m = 6)*
| E | s, V** | t, e−1** | r |
| ER0 | -2.743 ± 1.466 | 0.4586 ± 0.2229 | 0.9438 |
| ERR0 | -2.887 ± 1.560 | 0.4969 ± 0.2372 | 0.9457 |
| E1/2 | -3.055 ± 1.557 | 0.5117 ± 0.2367 | 0.9487 |
Table 1f.
Correlations of A values with E
R0, E
RR0, E
1/2 values (
vs saturated Hg
2Cl
2 electrode) obtained on XC
6H
4N
+≡N cations titration by sodium methylate in acetonitrile medium [
10] (m = 6)
*
Table 1f.
Correlations of A values with ER0, ERR0, E1/2 values (vs saturated Hg2Cl2 electrode) obtained on XC6H4N+≡N cations titration by sodium methylate in acetonitrile medium [10] (m = 6)*
| E | u, eV** | v, e** | r |
| ER0 | 6.046 ± 0.282 | 1.942 ± 0.944 | 0.9438 |
| ERR0 | 5.892 ± 0.345 | 1.800 ± 0.859 | 0.9457 |
| E1/2 | 6.030 ± 0.275 | 1.759 ± 0.814 | 0.9487 |
Reduction modes in
Table 1a,
Table 1b mean quite different oxidation conditions (different oxidants, reaction media and measurement techniques) and represent no subject of data comparison in respect to the computed results. The decision what relationship in
Table 1a,
Table 1b and
Table 2a,
Table 2b is to be used, depends upon the oxidation mode for which the predictions are to be performed.
The existence of symbate quantitative interrelationships presented above has its simple explanation: the easier the electron addition to diazonium cation, the easier is the reduction of the latter.
In a number of cases, relatively high (though satisfactory for regression analysis) are confidence limits about the slope and about the intercept. That does not decrease a predictive ability of the relationships stated. For the corresponding evaluations, of importance is a centre of statistical distribution. Many authors publish coefficients in regression equations without data on error, which often exceeds absolute values of the coefficients. Especially as one could hardly expect the narrow confidence limits: thermodynamic characteristics of a complex chemical reaction in solution or of a heterogeneous electrochemical process are compared to gaseous-phase quantity. Even great r values are remarkable here.
In some cases the first digit of confidence limits coincides with the first significant digit of regression coefficients. Following the rules of rounding figures in a literal sense would result in rough estimates. E. g., for the aryldiazonium cations reduction by potassium methylate in acetone, one must write g = 0.4 ± 0.1 instead of g = 0.3774 ± 0.1216. But a centre of statistical distribution shifts therewith, i. e. the result becomes erroneous. The data presentation as g = 0.3774 ± 0.1 distorts the approximation limits. Therefore, following the commonly accepted experience we give for the coefficients and confidence limits the equal number of digit places, but not the significant figures.
An argument in support of presenting “extra” significant digits consisits in the fact that the a-v values are intermediate on estimating the potentials or electron affinities. Rounding off is reasonable for final results.
All the aforesaid about confidence limits and a number of significant digits is valid also for the subsequent discussion.
Dependence of one-electron reduction potentials, dimerization potentials, half-equivalent potentials on titration of aryldiazonium cations by sodium methylate upon the stabilization energies of radicals
For theoretical estimation of the E, ER0, ERR0, E1/2 values it’s reasonable also to use correlations with the stabilization energies of radicals appearing on diazonia reduction.
One can make a logical supposition that for the reactions of diazonium cations reduction, the principle of linear free energy relationships (LFER) [
12,
49,
50,
51] is valid, according to which
where k and k
0 are rate constants of any reaction for the compound under study and reference one, respectively; ΔW is a change in some value characterizing the thermodynamic stability of these two substances or their reactive complexes.
Otherwise speaking, provided that a reduction potential is regarded as an analog of activation barrier on reduction and the LFER principle is assumed to be valid, thus an activation energy must be related linearly to a reaction free energy. The main component of the latter is a stabilization energy of radical [
52] - the difference between energies of a radical and a molecular system it is formed from.
Since the reduction potentials of diazonium cations and the stabilization energies of radicals formed on their basis are thermodynamic quantities with similar physical meanings, thus a linearity of their interrelation is sufficiently obvious even without the LFER principle involvement.
We have established the linear antibate dependences of the E, E
R0, E
RR0, E
1/2 values with the stabilization energies of radicals presented in the form of differences of enthalpies (ΔΔH
f) or free energies (ΔΔG
f) of formation of radicals and the corresponding aryldiazonium cations (two correlations below;
Table 2a,
Table 2b,
Table 2c,
Table 2d,
Table 2e and
Table 2f).
Herewith presented are interrelationships of half-wave potentials (E) of polarographic reduction of aryldiazonium XC
6H
4N
+≡N (X = H, 2-CH
3, 3-CH
3, 4-CH
3, 4-CN, 4-N(CH
3)
2, 2-OCH
3, 4-OCH
3, 2-Cl, 3-Cl, 4-Cl, 3-Br, 4-Br, 4-I) tetrafluoroborates in sulfolane [
4,
9] measured
vs. saturated Hg
2Cl
2 electrode, and energies (ΔΔH
f, ΔΔG
f) of radicals stabilization (m = 14; e is the electron charge):
Calorie-based units are usually used in periodicals and other kinds of permanent literature, as well as in handbooks on thermodynamics, quantum chemistry,
etc. 1 cal = 4.184 J. Dimensional representation of b and d coefficients could be also [mol/(4.184
.10
3 C)].
Correlation of frequencies in IR spectra of aryldiazonium cations with bonds orders, charges on atoms, mesomeric dipole moments, electron affinities
As it has been mentioned in the Introduction, to judge at once the stability of diazonium salts in respect to nitrogen elimination and their electrophilic reactivity, it’s of importance to possess information on the frequencies of stretching vibrations in molecular fragment C-N+≡N.
Taking into account that a bond energy is contributed substantially by a resonance energy [
28]
where p
ψω is the order of bond between ψ and ω atoms, β
ψω is resonance integral, one could suggest a linear relation of stretching vibrational frequencies with bond orders.
Table 2a.
Correlations of redox potentials
* (E) obtained on XC
6H
4N
+≡N cations titration, potentials (E) of polarographic reduction (
vs. saturated Hg
2Cl
2 electrode) [
5,
6,
7,
11], with enthalpies (ΔΔH
f) of radicals stabilization
Table 2a.
Correlations of redox potentials* (E) obtained on XC6H4N+≡N cations titration, potentials (E) of polarographic reduction (vs. saturated Hg2Cl2 electrode) [5,6,7,11], with enthalpies (ΔΔHf) of radicals stabilization
| Reduction mode | Set of substituents X | m | f, V** | g, V.mol/kcal** | r |
| 1 | H, 3-NO2, 4-NO2, 3-Cl, 4-Cl | 5 | -2.577 ± 0.817 | -0.01685 ± 0.00459 | -0.9892 |
| 2 | H, 4-NO2, 3-Cl, 4-Cl | 4 | -3.816 ± 2.415 | -0.02402 ± 0.01368 | -0.9829 |
| 3 | 3-NO2, 4-NO2, 4-SO2CF3, 3-Cl, 4-Cl, 3-Br, 4-I | 7 | -1.365 ± 0.815 | -0.009843 ± 0.004550 | -0.9278 |
| 4 | H, 4-CH3, 4-N(CH3)2, 3-NO2, 4-NO2, 4-OCH3, 4-SO2CF3, 3-Cl, 4-Cl, 3-Br, 4-Br | 11 | -2.783 ± 1.149 | -0.01778 ± 0.00659 | -0.8974 |
| 5 | 3-NO2, 4-NO2, 4-OCH3, 4-SO2CF3, 3-Cl, 3-Br | 6 | -3.327 ± 1.586 | -0.02057 ± 0.00892 | -0.9546 |
| 6 | H, 4-N(CH3)2, 3-NO2, 4-NO2, 3-Cl, 4-Cl, 4-Br | 7 | -3.672 ± 1.530 | -0.02268 ± 0.00873 | -0.9482 |
| 7 | H, 3-CH3, 4-CH3, 4-N(CH3)2, 3-NO2, 4-NO2, 4-OCH3, 3-F, 4-F, 4-SO2CF3, 3-Cl, 4-Cl,3-Br, 4-Br | 14 | -2.940 ± 0.830 | -0.01857 ± 0.00476 | -0.9261 |
| 8 | H, 3-CH3, 4-CH3, 4-N(CH3)2, 3-NO2, 4-NO2, 4-OCH3, 3-F, 4-F, 3-Cl, 4-Cl, 3-Br, 4-Br | 13 | -2.974 ± 1.116 | -0.01866 ± 0.00643 | -0.8874 |
Table 2b.
Correlations of redox potentials
* (E) obtained on XC
6H
4N
+≡N cations titration, potentials (E) of polarographic reduction (
vs. saturated Hg
2Cl
2 electrode) [
5,
6,
7,
11], with free energies (ΔΔG
f) of radicals stabilization
Table 2b.
Correlations of redox potentials* (E) obtained on XC6H4N+≡N cations titration, potentials (E) of polarographic reduction (vs. saturated Hg2Cl2 electrode) [5,6,7,11], with free energies (ΔΔGf) of radicals stabilization
| Reduction mode | Set of substituents X | m | h, V** | i, V.mol/kcal** | r |
| 1 | H, 3-NO2, 4-NO2, 3-Cl, 4-Cl | 5 | -2.894 ± 2.718 | -0.01864 ± 0.01518 | -0.9660 |
| 2 | H, 4-NO2, 3-Cl, 4-Cl | 4 | -4.545 ± 3.191 | -0.02819 ± 0.01810 | -0.9784 |
| 3 | 3-NO2, 4-NO2, 4-SO2CF3, 3-Cl, 4-Cl, 3-Br, 4-I | 7 | -1.457 ± 0.953 | -0.01036 ± 0.00532 | -0.9131 |
| 4 | H, 4-CH3, 4-N(CH3)2, 3-NO2, 4-NO2, 4-OCH3, 4-SO2CF3, 3-Cl, 4-Cl, 3-Br, 4-Br | 11 | -2.907 ± 1.172 | -0.01848 ± 0.00672 | -0.9008 |
| 5 | 3-NO2, 4-NO2, 4-OCH3, 4-SO2CF3, 3-Cl, 3-Br | 6 | -3.459 ± 1.527 | -0.02133 ± 0.00859 | -0.9604 |
| 6 | H, 4-N(CH3)2, 3-NO2, 4-NO2, 3-Cl, 4-Cl, 4-Br | 7 | -3.911 ± 1.431 | -0.02405 ± 0.00817 | -0.9590 |
| 7 | H, 3-CH3, 4-CH3, 4-N(CH3)2, 3-NO2, 4-NO2, 4-OCH3, 3-F, 4-F, 4-SO2CF3, 3-Cl, 4-Cl, 3-Br, 4-Br | 14 | -3.041 ± 0.860 | -0.01913 ± 0.00492 | -0.9955 |
| 8 | H, 3-CH3, 4-CH3, 4-N(CH3)2, 3-NO2, 4-NO2, 4-OCH3, 3-F, 4-F, 3-Cl, 4-Cl, 3-Br, 4-Br | 13 | -3.084 ± 1.173 | -0.01928 ± 0.00676 | -0.8843 |
Table 2c.
Correlations of standard potentials of reductive dimerization (E
RR0), semineutralization potentials (E
1/2) (
vs saturated Hg
2Cl
2 electrode) obtained on XC
6H
4N
+≡N cations titration by sodium sulphite [
7,
8], with enthalpies (ΔΔH
f) of radicals stabilization (m = 7)
*
Table 2c.
Correlations of standard potentials of reductive dimerization (ERR0), semineutralization potentials (E1/2) (vs saturated Hg2Cl2 electrode) obtained on XC6H4N+≡N cations titration by sodium sulphite [7,8], with enthalpies (ΔΔHf) of radicals stabilization (m = 7)*
| E | j, V** | k, V.mol/kcal** | r |
| ERR0 | -2.605 ± 0.994 | -0.01666 ± 0.00561 | -0.9596 |
| E1/2 | -2.476 ± 1.178 | -0.01599 ± 0.00665 | -0.9403 |
Table 2d.
Correlations of standard potentials of reductive dimerization (E
RR0), semineutralization potentials (E
1/2)(
vs saturated Hg
2Cl
2 electrode) obtained on XC
6H
4N
+≡N cations titration by sodium sulphite [
7,
8], with free energies (ΔΔG
f) of radicals stabilization (m = 7)
*
Table 2d.
Correlations of standard potentials of reductive dimerization (ERR0), semineutralization potentials (E1/2)(vs saturated Hg2Cl2 electrode) obtained on XC6H4N+≡N cations titration by sodium sulphite [7,8], with free energies (ΔΔGf) of radicals stabilization (m = 7)*
| E | l, V** | n, V.mol/kcal** | r |
| ERR0 | -2.934 ± 1.066 | -0.01852 ± 0.00602 | -0.9623 |
| E1/2 | -2.795 ± 1.267 | -0.01779 ± 0.00715 | -0.9439 |
Table 2e.
Correlations of E
R0, E
RR0, E
1/2 values (
vs saturated Hg
2Cl
2 electrode) obtained on XC
6H
4N
+≡N cations titration by sodium methylate in acetonitrile medium [
10], with enthalpies (ΔΔH
f) of radicals stabilization (m = 6)
*
Table 2e.
Correlations of ER0, ERR0, E1/2 values (vs saturated Hg2Cl2 electrode) obtained on XC6H4N+≡N cations titration by sodium methylate in acetonitrile medium [10], with enthalpies (ΔΔHf) of radicals stabilization (m = 6)*
| E | s, V** | t, V.mol/kcal** | r |
| ER0 | -4.142 ± 1.552 | -0.02473 ± 0.00873 | -0.9691 |
| ERR0 | -4.345 ± 1.689 | -0.02648 ± 0.00951 | -0.9681 |
| E1/2 | -4.556 ± 1.658 | -0.02727 ± 0.00933 | -0.9709 |
Table 2f.
Correlations of E
R0, E
RR0, E
1/2 values (
vs saturated Hg
2Cl
2 electrode) obtained on XC
6H
4N
+≡N cations titration by sodium methylate in acetonitrile medium [
10], with free energies (ΔΔG
f) of radicals stabilization (m = 6)
*
Table 2f.
Correlations of ER0, ERR0, E1/2 values (vs saturated Hg2Cl2 electrode) obtained on XC6H4N+≡N cations titration by sodium methylate in acetonitrile medium [10], with free energies (ΔΔGf) of radicals stabilization (m = 6)*
| E | u, V** | v, V.mol/kcal** | r |
| ER0 | -4.818 ± 2.043 | -0.02851 ± 0.01149 | -0.9604 |
| ERR0 | -5.057 ± 2.268 | -0.03045 ± 0.01276 | -0.9574 |
| E1/2 | -5.295 ± 2.226 | -0.03140 ± 0.01252 | -0.9612 |
Indeed, we have found the correlations of frequencies characterizing the assemblage of stretching vibrations of the fragment C-N
+≡N bonds [
16,
17,
18,
19,
20,
21,
53] with the N≡N and C-N bond orders (
Table 3a,
Table 3b and
Table 3c,
Figure 2).
Table 3a.
Correlations of stretching vibrational frequencies (ν) for fragment C-N
+≡N bonds in aryldiazonium 4-XC
6H
4N
+≡NY
− tetrafluoroborates and chlorides [
17] (in vaseline oil), with C-N bond orders (p) (m = 6)
*
Table 3a.
Correlations of stretching vibrational frequencies (ν) for fragment C-N+≡N bonds in aryldiazonium 4-XC6H4N+≡NY− tetrafluoroborates and chlorides [17] (in vaseline oil), with C-N bond orders (p) (m = 6)*
| Y | a, cm−1** | b, cm−1** | r |
| BF4 | 3164.2 ± 548.7 | -861.2 ± 536.5 | -0.9123 |
| Cl | 3179.5 ± 355.2 | -877.1 ± 347.2 | -0.9616 |
Table 3b.
Correlations of stretching vibrational frequencies (ν) for fragment C-N
+≡N bonds in aryldiazonium cations XC
6H
4N
+≡N [
53], with N≡N and C-N bond orders (p)
Table 3b.
Correlations of stretching vibrational frequencies (ν) for fragment C-N+≡N bonds in aryldiazonium cations XC6H4N+≡N [53], with N≡N and C-N bond orders (p)
| Anion | Condi-tions* | Set of substituents X | Bond | m | c, cm−1** | d, cm−1** | r |
| BF4− | 1 | H, 2-CH3, 3-CH3, 4-CH3, 2-CF3, 3-CF3, 4-NH2, 4-N(CH3)2, 4-N(C2H5)2, 2-NO2, 3-NO2, 4-NO2, 4-OCH3 | N≡N | 13 | -1402.5 ± 696.7 | 1296.3 ± 246.1 | 0.9614 |
| C-N | 13 | 3531.3 ± 235.7 | -1220.6 ± 227.5 | -0.9630 |
| BF4− | 2 | H, 2-CH3, 3-CH3, 4-CH3, 2-CF3, 4-N(CH3)2, 4-N(C2H5)2, 2-NO2, 3-NO2, 4-NO2, 4-OCH3 | N≡N | 11 | -846.8 ± 640.2 | 1095.9 ± 225.9 | 0.9647 |
| C-N | 11 | 3318.7 ± 229.9 | -1027.0 ± 222.7 | -0.9612 |
| BF4− | 3 | H, 2-CH3, 3-CH3, 4-CH3, 2-NO2 | N≡N | 5 | 702.4 ± 581.7 | 553.8 ± 204.1 | 0.9789 |
| C-N | 5 | 2847.0 ± 246.9 | -557.7 ± 243.2 | -0.9786 |
| PF6− | 1 | H, 2-CH3, 3-CH3, 4-CH3, 2-CF3, 3-CF3, 4-N(CH3)2, 4-N(C2H5)2, 2-NO2, 3-NO2, 4-NO2 | N≡N | 11 | -1171.7 ± 653.2 | 1213.7 ± 230.1 | 0.9697 |
| C-N | 11 | 3456.6 ± 220.7 | -1152.0 ± 214.5 | -0.9710 |
| PF6− | 2 | H, 2-CH3, 3-CH3, 4-CH3, 2-CF3, 4-N(CH3)2, 4-N(C2H5)2 | N≡N | 7 | -1138.6 ± 864.6 | 1198.8 ± 306.3 | 0.9761 |
| C-N | 7 | 3415.0 ± 312.3 | -1121.2 ± 299.1 | -0.9742 |
| CdCl42− | 1 | H, 3-CH3, 4-N(CH3)2, 4-N(C2H5)2 | N≡N | 4 | -1028.5 ± 726.8 | 1158.8 ± 259.1 | 0.9974 |
| C-N | 4 | 3373.3 ± 257.3 | -1084.1 ± 242.0 | -0.9973 |
| CdCl42− | 2 | H, 3-CH3, 4-N(CH3)2, 4-N(C2H5)2 | N≡N | 4 | -1148.5 ± 834.9 | 1202.4 ± 297.6 | 0.9967 |
| C-N | 4 | 3417.2 ± 353.2 | -1123.3 ± 332.2 | -0.9953 |
| HgCl42− | 1 | H, 2-CH3, 3-CH3, 4-CH3, 2-CF3, 3-CF3, 4-N(CH3)2, 4-N(C2H5)2, 2-NO2, 3-NO2, 4-NO2, 4-OCH3 | N≡N | 12 | -701.6 ± 496.0 | 1041.7 ± 174.9 | 0.9732 |
| C-N | 12 | 3258.9 ± 186.6 | -976.8 ± 181.0 | -0.9673 |
| HgCl42− | 2 | H, 2-CH3, 3-CH3, 4-CH3, 4-N(CH3)2, 4-N(C2H5)2, 2-NO2, 3-NO2, 4-NO2, 4-OCH3 | N≡N | 10 | -794.4 ± 673.7 | 1075.9 ± 237.9 | 0.9654 |
| C-N | 10 | 3296.3 ± 249.0 | -1009.2 ± 240.4 | -0.9602 |
Table 3c.
Correlations of stretching vibrational frequencies (ν) for fragment C-N
+≡N bonds in aryldiazonium XC
6H
4N
+≡N salts [
16,
18,
19,
20], with N≡N and C-N bond orders (p)
Table 3c.
Correlations of stretching vibrational frequencies (ν) for fragment C-N+≡N bonds in aryldiazonium XC6H4N+≡N salts [16,18,19,20], with N≡N and C-N bond orders (p)
| Conditions* | Set of substituents X | Bond | m | e, cm−1** | f, cm−1** | r |
| 1 | H, 3-CH3, 4-CH3, 4-COCH3, 3-COOCH3, 4-COOCH3, 4-COOC2H5, 4-NH2, 4-N(CH3)2, 4-NHCOCH3, 3-NO2, 4-NO2, 4-OH, 3-OCH3, 4-OCH3, 4-F, 4-SO2NH2, 3-Cl, 4-Cl, 4-Br, 4-I | N≡N | 21 | -1508.9 ± 508.4 | 1334.6 ± 179.2 | 0.9633 |
| C-N | 21 | 3519.1 ± 182.2 | -1207.2 ± 177.0 | -0.9571 |
| 2 | H, 2-CH3, 3-CH3, 4-CH3, 3-COOCH3, 4-COOCH3, 2-COOC2H5, 4-COOC2H5, 2-NO2, 3-NO2, 4-NO2, 2-OH, 4-OH, 3-OCH3, 4-OCH3, 2-Cl, 3-Cl,4-Cl, 4-Br | C-N | 19 | 3164.1 ± 280.2 | -857.2 ± 274.6 | -0.8497 |
| 3 | H, 2-CH3, 3-CH3, 4-CH3, 3-COOCH3, 4-COOCH3, 2-COOC2H5, 4-COOC2H5, 2-NO2, 3-NO2, 4-NO2, 2-OH, 4-OH, 3-OCH3, 4-OCH3, 2-Cl, 3-Cl,4-Cl, 4-Br | C-N | 19 | 3057.1 ± 208.2 | -756.6 ± 204.0 | -0.8847 |
| 4 | H, 2-CH3, 3-CH3, 4-CH3, 3-COOCH3, 4-COOCH3, 3-NO2, 4-NO2, 4-OH, 3-OCH3, 4-OCH3, 2-Cl, 3-Cl, 4-Cl, 4-Br | C-N | 15 | 3162.6 ± 274.6 | -858.9 ± 268.5 | -0.8867 |
| 5 | H, 2-CH3, 3-CH3, 4-CH3, 2-COOC2H5, 4-COOC2H5, 2-NO2, 3-NO2, 4-NO2, 2-OH, 3-OH, 4-OH, 2-OCH3, 3-OCH3, 4-OCH3, 2-Cl, 3-Cl, 4-Cl, 4-Br | C-N | 19 | 3192.4 ± 260.8 | -892.5 ± 255.6 | -0.8737 |
| 6 | H, 4-CH3, 4-COC6H5, 3-COOCH3, 4-COOCH3, 4-COOC2H5, 4-N(CH3)2, 4-NHCOCH3, 4-NO2, 4-OH, 4-OCH3, 4-F, 4-SO2NH2, 4-Cl,4-Br, 4-I | N≡N | 16 | -1233.3 ± 643.2 | 1235.7 ± 226.8 | 0.9524 |
Figure 2.
Dependence of stretching vibrational frequencies (ν, cm−1) (in vaseline oil) for fragment C-N+≡N bonds in aryldiazonium XC6H4N+≡N cations upon computed N≡N bond orders (p). X = H, 3-CH3, 4-CH3, 4-COCH3, 3-COOCH3, 4-COOCH3, 4-COOC2H5, 4-NH2, 4-N(CH3)2, 4-NHCOCH3, 3-NO2, 4-NO2, 4-OH, 3-OCH3, 4-OCH3, 4-F, 4-SO2NH2, 3-Cl, 4-Cl, 4-Br, 4-I. Correlation coefficient r = 0.9633.
Figure 2.
Dependence of stretching vibrational frequencies (ν, cm−1) (in vaseline oil) for fragment C-N+≡N bonds in aryldiazonium XC6H4N+≡N cations upon computed N≡N bond orders (p). X = H, 3-CH3, 4-CH3, 4-COCH3, 3-COOCH3, 4-COOCH3, 4-COOC2H5, 4-NH2, 4-N(CH3)2, 4-NHCOCH3, 3-NO2, 4-NO2, 4-OH, 3-OCH3, 4-OCH3, 4-F, 4-SO2NH2, 3-Cl, 4-Cl, 4-Br, 4-I. Correlation coefficient r = 0.9633.
In
Table 3b,
Table 3c, confidence limits about the c or e parameter are much greater in relative magnitude for the N≡N than for the C-N bond. Such a situation is not stipulated by vibrational effects, since bond order computations do not include vibrational contributions. The semiempirical PM3 method has been parameterized using a set of electroneutral and charged species. Thus, the PM3 is fit for species with charge equal to +1. However, diazonia are absent among the molecular systems of the set chosen for the parameterization. Then, for N
2, the PM3-computed heat of formation exceeds the experimental value by 17.6 kcal/mol [
26]. For the above possible reasons, the PM3 method may be more adequate for the C-N bond order evaluation, than for the N≡N one. Nevertheless, the correlation coefficient r values are sufficiently high in all cases, and the predictive interrelations obtained are valid, since the centre of statistical distribution is more important than confidence limits about the slope and about the intercept.
We shall now highlight two important points.
1. Vibrational frequencies of diazonium cations decrease with increasing π-electron-donor ability of substituents [
54,
55] in 2 and 4 positions:
Furthermore, for 4-substituted phenyldiazonium cations, the frequencies [
16,
18,
19,
20] are related linearly to the charges on carbon atoms in
para positions of monosubstituted benzenes’ aromatic rings (q
para) computed by the CNDO/2 method [
54,
55] (
Table 4a).
Table 4a.
Correlations of stretching vibrational frequencies (ν) for fragment C-N
+≡N bonds in aryldiazonium cations 4-XC
6H
4N
+≡N [
16,
18,
19,
20], with charges (q
para) on carbon atoms in aromatic rings
Table 4a.
Correlations of stretching vibrational frequencies (ν) for fragment C-N+≡N bonds in aryldiazonium cations 4-XC6H4N+≡N [16,18,19,20], with charges (qpara) on carbon atoms in aromatic rings
| Conditions* | Set of substituents X | m | a, cm−1** | b, cm−1** | r |
| 1 | H, CH3, NH2, N(CH3)2, OH, OCH3 | 6 | 2292.2 ± 41.2 | 3493.2 ± 2036.9 | 0.9220 |
| 1*** | H, CH3, OH, OCH3 | 4 | 2287.7 ± 15.2 | 2023.8 ± 1061.2 | 0.9855 |
| 2 | H, CH3, OH, OCH3 | 4 | 2285.7 ± 11.8 | 1639.6 ± 822.5 | 0.9867 |
| 3 | H, CH3, OH, OCH3 | 4 | 2283.8 ± 5.8 | 1381.7 ± 402.0 | 0.9955 |
| 4 | H, CH3, OH, OCH3 | 4 | 2283.5 ± 6.3 | 1566.0 ± 439.7 | 0.9958 |
| 5 | H, CH3, OH, OCH3 | 4 | 2279.5 ± 1.7 | 1698.1 ± 119.6 | 1.000 |
| 6† | H, CH3, OH, OCH3 | 4 | 2277.5 ± 15.4 | 1726.6 ± 1071.8 | 0.9798 |
The index q
para is assigned to a mesomeric effect of substituents in aromatic molecules [
54,
55,
62]. For substantiating the aforesaid we’ll note that the atomic groups electronegativity effect is extended over not more than three chemical bonds and disappears rapidly [
12,
50,
51,
54,
55]. At the same time, the mesomeric effect decays more slowly: it is transferred through three alternating bonds, even if vacant orbitals or negatively charged atoms do not take part in conjugation [
50].
The substituents mesomeric effect is carried over
ortho and
para positions of aromatic ring by means of the same mechanism [
12,
16,
50,
51,
56]. It’s no wonder therefore that for the frequencies (measured in acetone [
16,
18,
19,
20]) in IR spectra of 2-substituted aryldiazonium cations, the linear interrelation of ν
vs q
para (m = 4): ν = c +dq
para, c = 2282.9 ± 10.9 (cm
−1), d = 1119.6 ± 756.4 (cm
−1), r = 0.9762 is also stated.
We have found the linear correlations of vibrational frequencies for 4-substituted phenyldiazonia with mesomeric dipole moments, as well as the relationships reciprocal of those, μ
m vs ν (two dependences below;
Table 4b,
Table 4c,
Table 4d,
Table 4e,
Table 4f and
Table 4g). Let us present interrelations of stretching vibrational frequencies (ν) for fragment C-N
+≡N bonds in aryldiazonium chlorides 4-XC
6H
4N
+≡NCl
− [
17], and mesomeric dipole moments of X (X = H, CH
3, NO
2, Cl) substituents defined as vector differences μ
m = μ
CH3X - μ
CH2=CHX [
56] (m = 4):
Table 4b.
Correlations of stretching vibrational frequencies (ν) for fragment C-N
+≡N bonds in aryldiazonium salts 4-XC
6H
4N
+≡NY
−*[
17], with mesomeric dipole moments
** of X substituents (m=5)
Table 4b.
Correlations of stretching vibrational frequencies (ν) for fragment C-N+≡N bonds in aryldiazonium salts 4-XC6H4N+≡NY−*[17], with mesomeric dipole moments** of X substituents (m=5)
| Y | e, cm−1*** | f, cm−1/D***+^ | r |
| BF4 | 2283.5 ± 12.9 | -30.25 ± 21.01 | -0.9354 |
| Cl | 2283.9 ± 13.3 | -28.60 ± 21.78 | -0.9238 |
Table 4c.
Correlations of mesomeric dipole moments
* of X substituents with stretching vibrational frequencies (ν) for fragment C-N
+≡N bonds in aryldiazonium salts 4-XC
6H
4N
+≡NY
−**[
17] (m = 5)
Table 4c.
Correlations of mesomeric dipole moments* of X substituents with stretching vibrational frequencies (ν) for fragment C-N+≡N bonds in aryldiazonium salts 4-XC6H4N+≡NY−**[17] (m = 5)
| Y | g, D*** | h, D/cm−1***+ | r |
| BF4 | 66.05 ± 45.88 | -0.02892 ± 0.02010 | -0.9354 |
| Cl | 68.15 ± 51.91 | -0.02984 ± 0.02273 | -0.9238 |
Table 4d.
Correlations of stretching vibrational frequencies (ν) for fragment C-N
+≡N bonds in aryldiazonium cations 4-XC
6H
4N
+≡N [
53], with mesomeric dipole moments of Xsubstituents
Table 4d.
Correlations of stretching vibrational frequencies (ν) for fragment C-N+≡N bonds in aryldiazonium cations 4-XC6H4N+≡N [53], with mesomeric dipole moments of Xsubstituents
| Substituent X position | Set of substituents X | Anion | Condi-tions* | Set of μm** values | m | n, cm−1*** | q, cm−1/D*** | r |
| 4 | H, NH2, N(CH3)2, NO2, OCH3 | BF4− | 1 | 2 | 5 | 2298.7 ± 38.7 | -61.90 ± 30.53 | -0.9658 |
| 4 | H, CH3, N(CH3)2, NO2, OCH3 | BF4− | 2 | 1 | 5 | 2277.7 ± 33.5 | -47.74 ± 35.81 | -0.9258 |
| 4 | H, N(CH3)2, NO2, OCH3 | BF4− | 2 | 2 | 4 | 2282.2 ± 27.8 | -47.87 ± 24.24 | -0.9864 |
| 4 | H, N(CH3)2, NO2 | PF6− | 1 | 2 | 3 | 2288.1 ± 20.2 | -53.29 ± 16.64 | -1.000 |
| 4 | H, N(CH3)2, NO2, OCH3 | HgCl42− | 1 | 2 | 4 | 2266.5 ± 27.7 | -43.64 ± 24.18 | -0.9838 |
| 2 | H, CH3, NO2 | BF4− | 3 | 1 | 3 | 2280.0 ± 0.4 | -19.81 ± 0.80 | -1.000 |
| 2 | H, CH3, CF3, NO2 | HgCl42− | 1 | 1 | 4 | 2263.9 ± 7.8 | -23.92 ± 18.10 | -0.9704 |
| 2 | H, CH3, CF3, NO2 | HgCl42− | 1 | 3 | 4 | 2266.7 ± 3.1 | -40.17 ± 12.69 | -0.9947 |
Table 4e.
Correlations of mesomeric dipole moments of X substituents with stretching vibrational frequencies (ν) for fragment C-N
+≡N bonds in aryldiazonium cations 4-XC
6H
4N
+≡N [
53]
Table 4e.
Correlations of mesomeric dipole moments of X substituents with stretching vibrational frequencies (ν) for fragment C-N+≡N bonds in aryldiazonium cations 4-XC6H4N+≡N [53]
| Substituent X position | Set of substituents X | Anion | Condi-tions* | Set of μm** values | m | s, D*** | t, D/cm−1*** | r |
| 4 | H, NH2, N(CH3)2, NO2, OCH3 | BF4− | 1 | 2 | 5 | 37.40 ± 16.71 | -0.01507 ± 0.00743 | -0.9658 |
| 4 | H, CH3, N(CH3)2, NO2, OCH3 | BF4− | 2 | 1 | 5 | 40.96 ± 30.40 | -0.01796 ± 0.01347 | -0.9258 |
| 4 | H, N(CH3)2, NO2, OCH3 | BF4− | 2 | 2 | 4 | 46.41 ± 23.19 | -0.02033 ± 0.01030 | -0.9864 |
| 4 | H, N(CH3)2, NO2 | PF6− | 1 | 2 | 3 | 42.91 ± 13.23 | -0.01875 ± 0.00586 | -1.000 |
| 4 | H, N(CH3)2, NO2, OCH3 | HgCl42− | 1 | 2 | 4 | 50.28 ± 27.52 | -0.02218 ± 0.01229 | -0.9838 |
| 2 | H, CH3, NO2 | BF4− | 3 | 1 | 3 | 115.11 ± 4.64 | -0.05049 ± 0.00203 | -1.000 |
| 2 | H, CH3, CF3, NO2 | HgCl42− | 1 | 1 | 4 | 89.13 ± 67.59 | -0.03938 ± 0.02981 | -0.9704 |
| 2 | H, CH3, CF3, NO2 | HgCl42− | 1 | 3 | 4 | 55.83 ± 17.65 | -0.02463 ± 0.00778 | -0.9947 |
Table 4f.
Correlations of stretching vibrational frequencies (ν) for fragment C-N
+≡N bonds in aryldiazonium cations 4-XC
6H
4N
+≡N [
16,
18,
19,
20], with mesomeric dipole moments of Xsubstituents
Table 4f.
Correlations of stretching vibrational frequencies (ν) for fragment C-N+≡N bonds in aryldiazonium cations 4-XC6H4N+≡N [16,18,19,20], with mesomeric dipole moments of Xsubstituents
| Set of substituents X | Condi-tions* | Set of μm** values | m | u, cm−1*** | v, cm−1/D*** | r |
| H, CH3, COCH3, COOC2H5, NH2, N(CH3)2, NO2, OCH3 | 1 | 1 | 8 | 2277.4 ± 23.5 | -58.50 ± 27.40 | -0.9054 |
| H, COCH3, NH2, N(CH3)2, NO2, OH, OCH3 | 1 | 2 | 7 | 2288.4 ± 12.2 | -58.10 ± 10.91 | -0.9870 |
| H, CH3, NO2, Cl, Br, I | 1 | 3 | 6 | 2296.0 ± 4.6 | -24.89 ± 13.26 | -0.9336 |
| H, CH3, COOC2H5, NO2, OCH3 | 2 | 1 | 5 | 2290.8 ± 7.1 | -35.41 ± 11.63 | -0.9848 |
| H, COOC2H5, NO2, OCH3 | 2 | 2 | 4 | 2294.9 ± 10.5 | -47.37 ± 16.38 | -0.9936 |
| H, CH3, COOC2H5, NO2, OCH3 | 3 | 1 | 5 | 2287.7 ± 4.8 | -28.53 ± 7.88 | -0.9886 |
| H, COOC2H5, NO2, OCH3 | 3 | 2 | 4 | 2291.3 ± 8.8 | -40.64 ± 13.79 | -0.9938 |
| H, CH3, NO2, OCH3 | 4 | 1 | 4 | 2288.6 ± 10.0 | -33.09 ± 15.69 | -0.9881 |
| H, NO2, OH, OCH3 | 4 | 2 | 4 | 2292.0 ± 11.3 | -45.32 ± 17.60 | -0.9918 |
| H, CH3, COOC2H5, NO2, OCH3 | 5 | 1 | 5 | 2284.1 ± 5.8 | -32.80 ± 9.50 | -0.9876 |
| H, NO2, OH, OCH3 | 5 | 2 | 4 | 2288.3 ± 17.5 | -48.48 ± 27.23 | -0.9834 |
| H, CH3, COOC2H5, N(CH3)2, NO2, OCH3 | 6 | 1 | 6 | 2275.9 ± 26.3 | -51.58 ± 30.00 | -0.9224 |
| H, N(CH3)2, NO2, OH, OCH3 | 6 | 2 | 5 | 2284.8 ± 18.3 | -55.73 ± 16.83 | -0.9868 |
| H, CH3, NO2, Cl, Br, I | 6 | 3 | 6 | 2290.9 ± 7.3 | -31.55 ± 21.03 | -0.9023 |
Table 4g.
Correlations of mesomeric dipole moments of X substituents with stretching vibrational frequencies (ν) for fragment C-N
+≡N bonds in aryldiazonium cations 4-XC
6H
4N
+≡N [
16,
18,
19,
20]
Table 4g.
Correlations of mesomeric dipole moments of X substituents with stretching vibrational frequencies (ν) for fragment C-N+≡N bonds in aryldiazonium cations 4-XC6H4N+≡N [16,18,19,20]
| Set of substituents X | Condi-tions* | Set of μm** values | m | α, D*** | β, D/cm−1*** | r |
| H, CH3, COCH3, COOC2H5, NH2, N(CH3)2, NO2, OCH3 | 1 | 1 | 8 | 31.96 ± 14.84 | -0.01404 ± 0.00656 | -0.9054 |
| H, COCH3, NH2, N(CH3)2, NO2, OH, OCH3 | 1 | 2 | 7 | 38.38 ± 7.08 | -0.01676 ± 0.00315 | -0.9870 |
| H, CH3, NO2, Cl, Br, I | 1 | 3 | 6 | 80.43 ± 42.73 | -0.03502 ± 0.01865 | -0.9336 |
| H, CH3, COOC2H5, NO2, OCH3 | 2 | 1 | 5 | 62.69 ± 20.58 | -0.02737 ± 0.00898 | -0.9848 |
| H, COOC2H5, NO2, OCH3 | 2 | 2 | 4 | 47.83 ± 16.43 | -0.02084 ± 0.00721 | -0.9936 |
| H, CH3, COOC2H5, NO2, OCH3 | 3 | 1 | 5 | 78.42 ± 21.66 | -0.03428 ± 0.00947 | -0.9886 |
| H, COOC2H5, NO2, OCH3 | 3 | 2 | 4 | 55.69 ± 18.79 | -0.02430 ± 0.00824 | -0.9938 |
| H, CH3, NO2, OCH3 | 4 | 1 | 4 | 67.52 ± 31.95 | -0.02950 ± 0.01399 | -0.9881 |
| H, NO2, OH, OCH3 | 4 | 2 | 4 | 49.76 ± 19.21 | -0.02171 ± 0.00843 | -0.9918 |
| H, CH3, COOC2H5, NO2, OCH3 | 5 | 1 | 5 | 67.95 ± 19.69 | -0.02975 ± 0.00862 | -0.9876 |
| H, NO2, OH, OCH3 | 5 | 2 | 4 | 45.66 ± 25.47 | -0.01995 ± 0.01120 | -0.9834 |
| H, CH3, COOC2H5, N(CH3)2, NO2, OCH3 | 6 | 1 | 6 | 37.58 ± 21.69 | -0.01649 ± 0.00959 | -0.9224 |
| H, N(CH3)2, NO2, OH, OCH3 | 6 | 2 | 5 | 39.93 ± 11.86 | -0.01747 ± 0.00527 | -0.9868 |
| H, CH3, NO2, Cl, Br, I | 6 | 3 | 6 | 59.04 ± 39.21 | -0.02575 ± 0.01717 | -0.9023 |
Due to the same-type character of transferring the atomic groups conjugation effect to
ortho and
para positions of aromatic ring [
12,
16,
50,
51,
56], the frequencies for 2-XC
6H
4N
+≡N cations correlate linearly with mesomeric dipole moments analogously to the situation with 4-substituted cations (
Table 4h,
Table 4i).
Table 4h.
Correlations of stretching vibrational frequencies (ν) for fragment C-N
+≡N bonds in aryldiazonium cations 2-XC
6H
4N
+≡N [
16,
18,
19,
20], with mesomeric dipole moments of X substituents
Table 4h.
Correlations of stretching vibrational frequencies (ν) for fragment C-N+≡N bonds in aryldiazonium cations 2-XC6H4N+≡N [16,18,19,20], with mesomeric dipole moments of X substituents
| Set of substituents X | Conditions* | Set of μm** values | m | γ, cm−1*** | δ, cm−1/D*** | r |
| H, CH3, COOC2H5, NO2, OCH3 | 1 | 1 | 5 | 2285.2 ± 6.8 | -20.04 ± 11.15 | -0.9577 |
| H, NO2, OH, OCH3 | 1 | 2 | 4 | 2288.5 ± 15.4 | -30.27 ± 23.99 | -0.9677 |
| H, CH3, COOC2H5, NO2, OCH3 | 2 | 1 | 5 | 2284.4 ± 6.0 | -19.79 ± 9.83 | -0.9647 |
Table 4i.
Correlations of mesomeric dipole moments of X substituents with stretching vibrational frequencies (ν) for fragment C-N
+≡N bonds in aryldiazonium cations 2-XC
6H
4N
+≡N [
16,
18,
19,
20]
Table 4i.
Correlations of mesomeric dipole moments of X substituents with stretching vibrational frequencies (ν) for fragment C-N+≡N bonds in aryldiazonium cations 2-XC6H4N+≡N [16,18,19,20]
| Set of substituents X | Conditions* | Set of μm** values | m | ε, D*** | ζ, D/cm−1*** | r |
| H, CH3, COOC2H5, NO2, OCH3 | 1 | 1 | 5 | 104.48 ± 58.13 | -0.04572 ± 0.02544 | -0.9577 |
| H, NO2, OH, OCH3 | 1 | 2 | 4 | 70.81 ± 55.88 | -0.03093 ± 0.02452 | -0.9677 |
| H, CH3, COOC2H5, NO2, OCH3 | 2 | 1 | 5 | 107.54 ± 53.42 | -0.04708 ± 0.02339 | -0.9647 |
In
Table 4d and
Table 4e there are four linear dependences with m = 3. For the number of points equal to three, the correlation coefficient differs from zero significantly for regression provided that it is exactly equal to unity. But even such a rigorous condition is met for the aforementioned data. The latter confirms the fact that the interrelations revealed are not of coincidental character.
2. Using 43 diazonium cations (all of these considered in the present work) as examples it has been elucidated that the changes in N≡N and C-N bond orders are of linear antibate character. Interdependences between N≡N and C-N bond orders (p) in XC
6H
4N
+≡N (X = H, 2-CH
3, 3-CH
3, 4-CH
3, 2-CF
3, 3-CF
3, 4-CF
3, 4-CCl
3, 4-CN, 4-COCH
3, 4-COC
6H
5, 3-COOCH
3, 4-COOCH
3, 2-COOC
2H
5, 4-COOC
2H
5, 4-NH
2, 4-NHCH
3, 4-N(CH
3)
2, 4-NHCOCH
3, 2-NO
2, 3-NO
2, 4-NO
2, 2-OH, 3-OH, 4-OH, 2-OCH
3, 3-OCH
3, 4-OCH
3, 3-F, 4-F, 4-Si(CH
3)
3, 4-SiCl
3, 4-SH, 4-SCH
3, 4-SO
2CF
3, 4-SO
2NH
2, 2-Cl, 3-Cl, 4-Cl, 3-Br, 4-Br, 4-I) cations (m = 43):
The validity of (1) and (2) conditions confirms that the electron-donor substituents in 2 and 4 positions stabilize the aryldiazonium cations by increasing a contribution of resonance structures, in which a bond between nitrogen atoms of diazo group is not triple but double, e. g., as it’s shown below for 4-hydroxyphenyldiazonium [
16]:
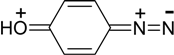
The more pronounced are π-electron-donor properties of a substituent in aromatic ring, the less is vibrational frequency ν, N≡N bond order (pNN) and the higher is the C-N bond order (pCN), i. e. the less favourably is diazonium cation disposed toward decomposition to produce nitrogen molecule.
In spite of the tendency to delocalizing the electron density in the C-N+≡N fragment’s interatomic basins, quinonediazide resonance forms contribute poorly to electronic structure of diazonium cations at any considered modes of substitution in aromatic ring. That is supported by the values of pNN (2.760 to 2.875) and pCN (0.991 to 1.110).
The more stable is aryldiazonium cation in respect to decomposition, the less it’s active as electrophilic agent. Thus the optimal structure (substituents’ nature and position) of diazonia presumes a compromise: diazonium ion must display a sufficiently high reactivity on azo coupling at poor capability of entering the elimination reaction. In order to provide an intensive analytical signal therewith, the chromophoric or auxochromic properties of substituting groups are desirable.
Relationship of mesomeric dipole moments and vibrational frequencies of aryldiazonium cations with electron affinities
In accordance with [
63], the potentials of polarographic oxidation and reduction of mono- and disubstituted benzenes are related linearly to the mesomeric dipole moments of atomic groups X. Because of usual correlation between the polarographic reduction potentials and the electron affinities of electroactive substances [
47], linear dependences would be naturally expected between the computed electron affinities and mesomeric dipole moments of substituents in aryldiazonium cations. Indeed, we have established the correlations of such type (
Table 5a).
The existence of relationships between the ν and μm values on the one hand, μm and A on the other offers a possibility of suggesting the occurrence of linear dependences between the stretching vibrational frequencies of the C-N+≡N fragment bonds in XC6H4N+≡N cations and Koopmans electron affinities.
We have found such relations allowing one to predict both the vibrational frequencies using the computed electron affinities (
Table 5b) and the difficult-to-determine electron affinity values by the experimental vibrational spectra (
Table 5c).
Table 5a.
Correlations of mesomeric dipole moments of X substituents with electron affinity (A) values for 4-XC6H4N+≡N cations
Table 5a.
Correlations of mesomeric dipole moments of X substituents with electron affinity (A) values for 4-XC6H4N+≡N cations
| Set of μm* values | Set of substituents X | m | a, D** | b, D/eV**+ | r |
| 1 | H, CH3, CF3, CCl3, CN, COCH3, COOC2H5, NH2, N(CH3)2, NO2, OCH3, Si(CH3)3, SiCl3, SCH3, Cl, Br, I | 17 | 10.28 ± 2.69 | -1.600 ± 0.425 | -0.9007 |
| 2 | H, CH3, CCl3, CN, N(CH3)2, NO2,F, Cl, Br, I | 10 | 13.84 ± 3.77 | -2.140 ± 0.590 | -0.9473 |
| 3 | H, COCH3, NH2, NHCH3, N(CH3)2, NO2, OH, OCH3, SH, SCH3 | 10 | 12.40 ± 2.76 | -1.900 ± 0.449 | -0.9604 |
Table 5b.
Interrelationships of stretching vibrational frequencies (ν) for fragment C-N
+≡N bonds and electron affinity (A) values for aryldiazonium cations 4-XC
6H
4N
+≡N [
53]
Table 5b.
Interrelationships of stretching vibrational frequencies (ν) for fragment C-N+≡N bonds and electron affinity (A) values for aryldiazonium cations 4-XC6H4N+≡N [53]
| Anion | Condi-tions* | Set of substituents X | m | c, сm−1** | d, сm−1/eV**+ | r |
| BF4− | 1 | H, 2-CH3, 3-CH3, 4-CH3, 2-CF3, 3-CF3, 4-NH2, 4-N(CH3)2, 4-N(C2H5)2, 2-NO2, 3-NO2, 4-NO2, 4-OCH3 | 13 | 1655.2 ± 187.9 | 97.34 ± 29.76 | 0.9083 |
| BF4− | 2 | H, 2-CH3, 3-CH3, 4-CH3, 2-CF3, 4-N(CH3)2, 4-N(C2H5)2, 2-NO2, 3-NO2, 4-NO2, 4-OCH3 | 11 | 1740.4 ± 165.6 | 82.14 ± 26.16 | 0.9212 |
| BF4− | 3 | H, 2-CH3, 3-CH3, 4-CH3, 2-NO2 | 5 | 2043.1 ± 131.4 | 37.22 ± 20.56 | 0.9606 |
| PF6− | 1 | H, 2-CH3, 3-CH3, 4-CH3, 2-CF3, 3-CF3, 4-N(CH3)2, 4-N(C2H5)2, 2-NO2, 3-NO2, 4-NO2 | 11 | 1702.7 ± 188.4 | 89.41 ± 29.48 | 0.9162 |
| PF6− | 2 | H, 2-CH3, 3-CH3, 4-CH3, 2-CF3, 4-N(CH3)2, 4-N(C2H5)2 | 7 | 1612.4 ± 299.4 | 103.36 ± 48.77 | 0.9251 |
| CdCl42− | 1 | H, 3-CH3, 4-N(CH3)2, 4-N(C2H5)2 | 4 | 1521.3 ± 256.3 | 118.67 ± 43.30 | 0.9929 |
| CdCl42− | 2 | H, 3-CH3, 4-N(CH3)2, 4-N(C2H5)2 | 4 | 1494.8 ± 59.91 | 124.04 ± 10.12 | 0.9996 |
| HgCl42− | 1 | H, 2-CH3, 3-CH3, 4-CH3, 2-CF3, 3-CF3, 4-N(CH3)2, 4-N(C2H5)2, 2-NO2, 3-NO2, 4-NO2, 4-OCH3 | 12 | 1761.4 ± 135.6 | 77.41 ± 21.32 | 0.9314 |
| HgCl42− | 2 | H, 2-CH3, 3-CH3, 4-CH3, 4-N(CH3)2, 4-N(C2H5)2, 2-NO2, 3-NO2, 4-NO2, 4-OCH3 | 10 | 1752.5 ± 198.2 | 79.61 ± 31.50 | 0.8996 |
Table 5c.
Interrelationships of electron affinity (A) values with stretching vibrational frequencies (ν) for fragment C-N
+≡N bonds in aryldiazonium cations 4-XC
6H
4N
+≡N [
53]
Table 5c.
Interrelationships of electron affinity (A) values with stretching vibrational frequencies (ν) for fragment C-N+≡N bonds in aryldiazonium cations 4-XC6H4N+≡N [53]
| Anion | Condi-tions* | Set of substituents X | m | e, eV** | f, eV/сm−1**+ | r |
| BF4− | 1 | H, 2-CH3, 3-CH3, 4-CH3, 2-CF3, 3-CF3, 4-NH2, 4-N(CH3)2, 4-N(C2H5)2, 2-NO2, 3-NO2, 4-NO2, 4-OCH3 | 13 | -12.92 ± 5.88 | 0.008474 ± 0.002591 | 0.9083 |
| BF4− | 2 | H, 2-CH3, 3-CH3, 4-CH3, 2-CF3, 4-N(CH3)2, 4-N(C2H5)2, 2-NO2, 3-NO2, 4-NO2, 4-OCH3 | 11 | -17.03 ± 7.43 | 0.01033 ± 0.00329 | 0.9212 |
| BF4− | 3 | H, 2-CH3, 3-CH3, 4-CH3, 2-NO2 | 5 | -49.82 ± 31.05 | 0.02464 ± 0.01362 | 0.9606 |
| PF6− | 1 | H, 2-CH3, 3-CH3, 4-CH3, 2-CF3, 3-CF3, 4-N(CH3)2, 4-N(C2H5)2, 2-NO2, 3-NO2, 4-NO2 | 11 | -14.97 ± 7.04 | 0.009390 ± 0.003096 | 0.9162 |
| PF6− | 2 | H, 2-CH3, 3-CH3, 4-CH3, 2-CF3, 4-N(CH3)2, 4-N(C2H5)2 | 7 | -12.47 ± 8.77 | 0.008280 ± 0.003907 | 0.9251 |
| CdCl42− | 1 | H, 3-CH3, 4-N(CH3)2, 4-N(C2H5)2 | 4 | -12.55 ± 6.74 | 0.008307 ± 0.003031 | 0.9929 |
| CdCl42− | 2 | H, 3-CH3, 4-N(CH3)2, 4-N(C2H5)2 | 4 | -12.01 ± 1.46 | 0.008056 ± 0.000657 | 0.9996 |
| HgCl42− | 1 | H, 2-CH3, 3-CH3, 4-CH3, 2-CF3, 3-CF3, 4-N(CH3)2, 4-N(C2H5)2, 2-NO2, 3-NO2, 4-NO2, 4-OCH3 | 12 | -18.90 ± 6.95 | 0.01121 ± 0.00309 | 0.9314 |
| HgCl42− | 2 | H, 2-CH3, 3-CH3, 4-CH3, 4-N(CH3)2, 4-N(C2H5)2, 2-NO2, 3-NO2, 4-NO2, 4-OCH3 | 10 | -16.62 ± 9.06 | 0.01017 ± 0.00402 | 0.8996 |
One of the independent variables used, A, is subject to error itself. However, such an error, being rather high in the case of experimental determinations and depending on experimental techniques considerably, within quantum chemical evaluations becomes approximately constant for the series of aryldiazonia with similar structure. The latter lets one obtain the above (
Table 5b,
Table 5c) predictive quantitative relationships.
Conclusion
Using the relationships deduced that combine the potentials with electron affinities and stabilization energies of radicals, one could predict the real values of E, ER0, ERR0, E1/2 and A not always available to the experimental measurement.
A priori evaluation of the said parameters by quantum chemical methods is important for molecular design of compounds with given properties (E, ER0, ERR0, E1/2, A), with predictible electrophilic reactivity, may serve as a base for expert decision on reasonability of synthesis that is sometimes labour- and time-consuming, requiring complicated device, rigid conditions, expensive and toxic chemicals.
The existence of linear dependences ν
vs q
para, ν
vs μ
m, p
NN vs p
CN testifies that the changes in frequencies and N≡N, C-N bond orders within the series of 4-XC
6H
4N
+≡N cations occur in accordance with the mesomeric effect of atomic groups X. The latter point is substantiated also by the presence of correlations [
18,
20] between the vibrational frequencies of diazonium cations and the resonance constants σ
+ characterizing the capacity of atomic groups X for polar conjugation [
56]. In general, the frequencies correlate also with the constants σ, σ
*, σ
meta, as well as the σ
0 values allowing for the inductive effect of substituted phenyls on the N≡N bond multiplicity [
18,
19,
20]. The N≡N bond multiplicities are related linearly to the σ values [
19].
Using the quantitative relationships combining the vibrational frequencies with bond orders, qpara quantities, mesomeric dipole moments, one could perform a target-oriented design of diazonium cations with the given stability and electrophilic reactivity, with the expected values of substituents mesomeric parameters, i. e. could synthesize directively the diazonium salts reactive in azo coupling processes and, at the same time, not entering a decay reaction competitive in respect to the key reaction.
The approach to establishing structure - property correlations developed in the present work with respect to the substituted phenyldiazonium cations, provided that the experimental estimations of reduction potentials and vibrational frequencies are available, could be extended over diazonium cations from another series.
The results obtained show that aryldiazonium cations present a series of molecular systems, on the basis of which the predictive interrelationships (alternative with respect to those proposed in the work [
44]) could be stated for evaluating the mesomeric dipole moments of atomic groups. If this problem is solved using the quantitative relations μ
mvs A, thus the substituted diazonium cations can be involved whether these exist or not really. An important point is solely that phenyldiazonium is appropriate “matrix”, on the basis of which the mesomeric effect of substituents is simulated.
The collection of experimental and computed data on reduction potentials, vibrational frequencies, the values of qpara, μm, will favour the enhancement of reliability of the corresponding quantitative relationships.
At the same time a significant amount of correlations (121, neglecting mutually reciprocal ones) and a sufficiently great number of points in many of them enable one to conclude that the relations found are not of random character and possess a predictive power.