Effect of Cyclization on the Magnitude and Anisotropy of the CSA Tensor
The changes in the
31P CSA tensors due to ring formation for a series of phosphate clusters are reported. We were particularly interested in highly condensed and cross-linked phosphate systems, such as might be observed in phosphate glasses. While there have been recent advances in
ab initio techniques for calculations of NMR parameters in large periodic systems [
12], the
ab initio method utilized in the present study requires the selection of isolated clusters for the actual calculations. To obtain these isolated clusters the explicit bonding or cross-linking to adjacent phosphate species is removed, with terminal P-OH groups taking the role of P-O-P linkages. In this manner it is possible to obtain clusters of manageable size for the geometry optimization and chemical shielding calculations.
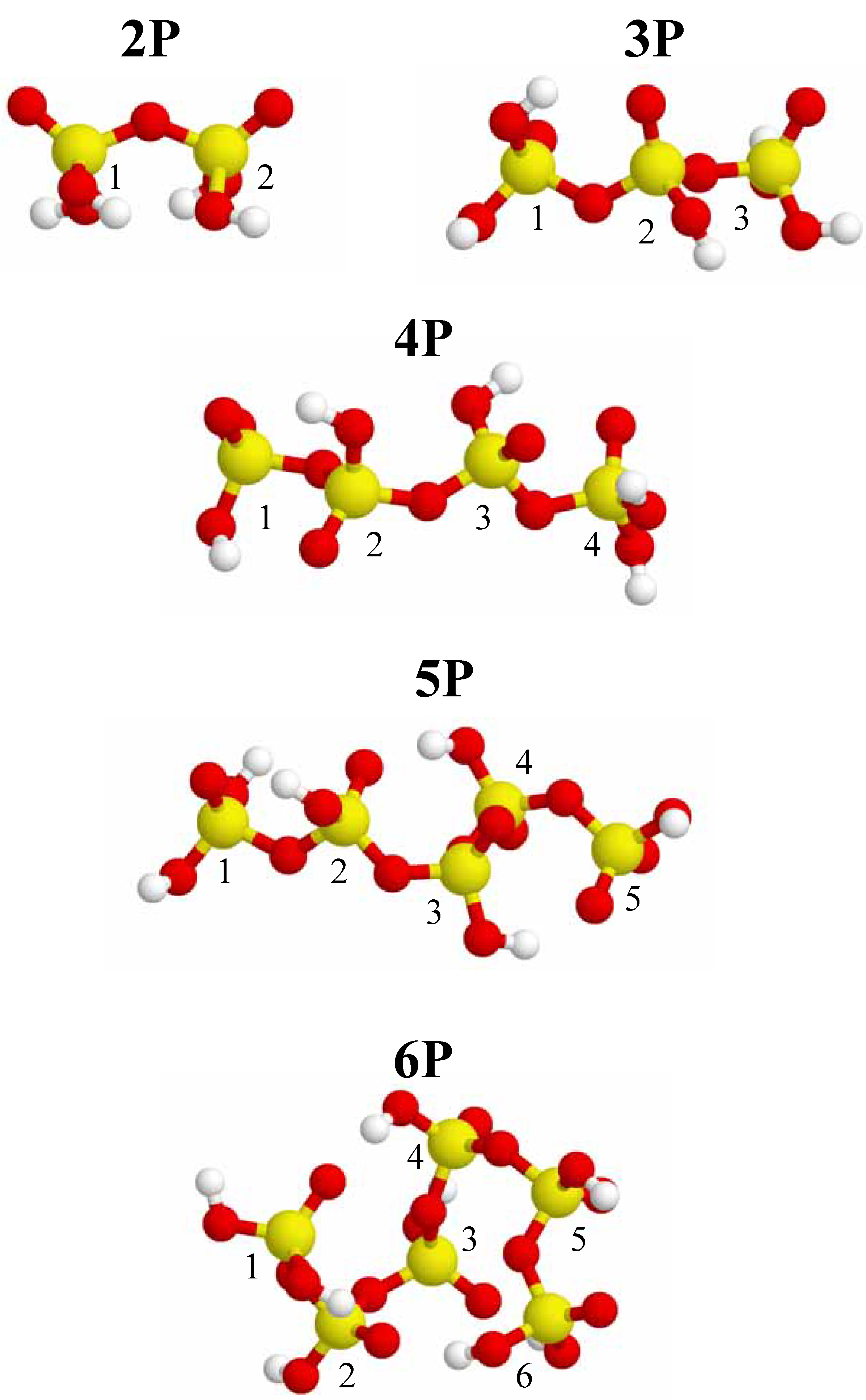
Figure 1.
Different optimized conformations for 2-P, 3-P, 4-P, 5-P and 6-P-membered acyclic phosphate clusters. Phosphorus is depicted as yellow, oxygen is red, and hydrogen is white. Each phosphorus nuclei has a number ID for identification with
31P CSA tensor values listed in
Table 1.
Figure 1.
Different optimized conformations for 2-P, 3-P, 4-P, 5-P and 6-P-membered acyclic phosphate clusters. Phosphorus is depicted as yellow, oxygen is red, and hydrogen is white. Each phosphorus nuclei has a number ID for identification with
31P CSA tensor values listed in
Table 1.
Figure 2.
Different conformations for 2-P, 3-P, and 4-P-membered cyclic phosphate clusters. Phosphorus is depicted as yellow, oxygen is red, and hydrogen is white. The +/ − nomenclature refers to the relative orientation of the terminal P=O bonds (see text for details). Each phosphorus nuclei has a number ID for identification with
31P CSA tensor values in
Table 2.
Figure 2.
Different conformations for 2-P, 3-P, and 4-P-membered cyclic phosphate clusters. Phosphorus is depicted as yellow, oxygen is red, and hydrogen is white. The +/ − nomenclature refers to the relative orientation of the terminal P=O bonds (see text for details). Each phosphorus nuclei has a number ID for identification with
31P CSA tensor values in
Table 2.
Figure 3.
Different conformations for 5-P and 6-P-membered cyclic clusters investigated. Phosphorus is depicted as yellow, oxygen is red, and hydrogen is white. The +/ − nomenclature refers to the relative orientation of the terminal P=O bonds (see text for details). Each phosphorus nuclei has a number ID for identification with
31P CSA tensor values in
Table 3 and
Table 4.
Figure 3.
Different conformations for 5-P and 6-P-membered cyclic clusters investigated. Phosphorus is depicted as yellow, oxygen is red, and hydrogen is white. The +/ − nomenclature refers to the relative orientation of the terminal P=O bonds (see text for details). Each phosphorus nuclei has a number ID for identification with
31P CSA tensor values in
Table 3 and
Table 4.
The results presented here were aimed at determining the effects of cyclization on the
31P chemical shielding in Q
3 type phosphate tetrahedral. The Q
n nomenclature designates the number of bridging P-O-P bonds (i.e. n) present on each phosphate tetrahedral. The phosphate clusters investigated therefore all contain one terminal P=O oxygen, one or two P-OH groups, and one or two P-O-P bonds. Recall that in these truncated clusters the P-OH bonds have been included to represent truncated P-O-P type bonding. It has been shown that the use of the OH substitution is more realistic than a simple H substitution during cluster truncation [
13]. Due to the presence of a P-OH bond in place of a P-O-P bond, the resulting absolute values of the
31P chemical shielding tensors will not match exactly with experimental values for Q
3 phosphate species, but the variations and trends observed in the
31P CSA tensor as a result of cyclization can be used to predict and identify similar changes that would occur in Q
3 phosphate species. Minimized conformations for both cyclic and acyclic phosphate clusters containing between two and six phosphate tetrahedral were calculated, and are shown in
Figure 1,
Figure 2 and
Figure 3. These mimized conformations represent the lowest energy conformation obtained from several sequential optimization runs. For the acyclic clusters the starting structure prior to optimization was the linear extended all
trans conformation. Note that the resulting minimized conformations observed for the acyclic phosphate clusters (
Figure 1) are not the classic all
trans conformations commonly encountered in the modeling of organic alkane chains. The minimized, low-energy structures show considerable curvature, with a large variation in the P-O-P and O-P-O bond angles due to the anisotropy of the P bonding, along with repulsive interactions. In general, the P-O-P bond angles range from 130
o to 139
o, while the terminal P-O-P bond angles in the smaller acyclic clusters were between 118
o and 123
o. These P-O-P bond angles compare to the 132
o and 140
o previously reported for the staggered and eclipsed conformations in the H
4P
2O
7 cluster, respectively [
5]. The O-P-O bond angles range from 100
o to 106
o, with the O-P-O
T bond angles (T denotes the terminal P=O oxygen) ranging from 115
o to 120
o. The anisotropy of the O-P-O bond angles from the ideal tetrahedral angle of 109
o is a major contributor to the non-linear minimized structures observed for the acyclic clusters (
Figure 1). In the optimized acyclic clusters the observed P=O bond lengths are ~1.44 Å, the P-OH bond lengths range from ~1.54 to 1.57 Å, with the P-O-P bond lengths being ~1.61 Å. These bond lengths are slightly different than the previous
ab initio results reported for the H
4P
2O
7 cluster [
5], but these length differences result from the smaller basis set used for optimization in the present study: HF 6-31+G(d) versus B3LYP 6-311++G(2d,2p) in previous studies .
Because every phosphate tetrahedral contains a terminal P=O bond, the relative orientation of these terminal oxygen bonds can lead to different ring conformations. For example, in a cyclic phosphate cluster containing only two phosphorus atoms, the relative orientation of the terminal P=O bonds can be on the same side of the ring (
cis) or on different sides of the ring (
trans). These two different ring conformations will be designated as ( + + ) and (+ − ), respectively. This +/− notation will be used to designate the various ring conformations for the different sized cyclic phosphate clusters investigated, and are shown in
Figure 2 and
Figure 3.
The
31P CSA tensors for the acyclic phosphate clusters as a function of the number of phosphate tetrahedral were calculated and are given in
Table 1. The isotropic chemical shielding, the individual tensor elements in the principal axis system (PAS), the tensor anisotropy and the CSA asymmetry parameter (as defined by Equations 1-3) are given. In the acyclic clusters there are both endgroup phosphate species (which contain two P-OH, one P=O and one P-O-P oxygen species) and a middle phosphate species (which contain one P-OH, one P=O, and two P-O-P oxygen species). In the larger acyclic clusters there is approximately a +10 ppm increase in the isotropic chemical shielding due to the change from a endgroup phosphate species to a middle phosphate species. The magnitude of this shift is similar to that observed experimentally between Q
3 and Q
2 or Q
2 and Q
1 phosphate species. A +18.8 ppm increase in shielding was noted between the endgroups and the middle phosphate species in a recent
ab initio calculation of the
31P CSA tensor in the P
3O
105- cluster [
7]. Experimentally an increase in shielding of +8.6 ppm and +10.8 ppm between the endgroup and middle phosphate species has been noted for the (
I) and (
II) crystal forms of the anhydrous Na
5P
3O
10 salts, respectively [
14]. Similarly, in crystalline K
5P
3O
10 an increase of +15.0 to +18.3 ppm has also been reported [
15,
16]. These experimental variations in the
31P chemical shielding are of similar magnitude observed for the
ab initio results on optimized acyclic clusters presented in
Table 1. On the other hand, it should be remembered that these clusters represent truncated Q
3 species. In general, endgroup phosphates containing both terminal oxygen and two hydroxyl species are not commonly observed. Close inspection of these optimized structures suggest that simple variations in the P-O-P bond angle are responsible for the observed difference between endgroup and middle phosphate species. The H
4P
2O
7 cluster, which contains two endgroup species with a P-O-P bond angle of 135
o, has an isotropic chemical shielding that is larger than observed for endgroup phosphate species in other clusters, and is within the same range seen for middle phosphate species (
Table 1). Similarly, the H
5P
3O
10 cluster exhibits a smaller difference in the chemical shift between the endgroup and middle phosphate species, but contains P-O-P bond angles of 138
o and 125
o. For the larger acyclic clusters these terminal P-O-P bond angles are significantly smaller, ranging from 118
o to 124
o. Variation of the isotropic chemical shielding (σ
iso) as a function of the P-O-P bond angle and the torsional or dihedral angle between O
b-P-O
b and P-O
t (where O
b and O
t designate the bonding and terminal oxygens respectively) have been studied using both empirical and
ab initio techniques [
2,
3]. Variations on the order of 15 to 25 ppm have been calculated for σ
iso in Q
3 species due to changes in the P-O-P bond angle. The variation of the
31P isotropic chemical shielding, as a function of P-O-P bond angle in the H
4P
2O
7 cluster have also been reported by Alam [
5]. In those
ab initio investigations it was shown that changes in the P-O-P bond angle was the structural variant that produced the largest change in the
31P CSA tensor. For that simple cluster, the isotropic chemical shielding increased with larger P-O-P bond angles, consistent with the trends observed in the present study. For the H
4P
2O
7 cluster, changes in the O
b-P-O
b / P-O
t torsional angle ϕ had minimal effect on the isotropic chemical shielding, but did produce significant changes in the CSA anisotropy (~30 ppm) for torsional angles greater than ~80
o [
5]. Therefore, for the phosphate clusters reported in this manuscript, the observed variations in the
31P CSA tensor are probably the result of changes in both the P-O-P bond angle and the O
b-P-O
b / P-O
t torsional angle.
Table 1.
Ab Initio NMR 31P CSA Tensors for Geometry Optimized Acyclic Phosphate Clusters.
Table 1.
Ab Initio NMR 31P CSA Tensors for Geometry Optimized Acyclic Phosphate Clusters.
| Cluster | IDa | Species | σiso(ppm) | σ33(ppm) | σ22(ppm) | σ11(ppm) | Δσ(ppm) | η |
| H4P2O7 | 1 | Endgroup | 374.5 | 541.7 | 297.8 | 284.0 | 250.8 | 0.08 |
| 2 | | 374.5 | 541.7 | 297.8 | 284.0 | 250.8 | 0.08 |
| H5P3O10 | 1 | Endgroup | 360.1 | 483.4 | 323.0 | 274.0 | 184.9 | 0.40 |
| 3 | | 363.9 | 517.5 | 304.0 | 270.2 | 230.4 | 0.22 |
| | | | | | | | |
| 2 | Middle | 366.2 | 483.3 | 327.7 | 287.7 | 175.6 | 0.34 |
| | | | | | | | |
| H6P4O13 | 1 | Endgroup | 364.9 | 506.1 | 314.5 | 274.1 | 211.8 | 0.29 |
| 4 | | 365.1 | 510.0 | 312.0 | 273.0 | 217.3 | 0.27 |
| | | | | | | | |
| 3 | Middle | 373.1 | 523.1 | 310.0 | 286.0 | 225.1 | 0.16 |
| 2 | | 374.7 | 530.5 | 312.2 | 281.5 | 233.6 | 0.20 |
| | | | | | | | |
| H7P5O16 | 1 | Endgroup | 361.8 | 482.5 | 324.9 | 278.0 | 181.0 | 0.39 |
| 5 | | 362.7 | 481.6 | 326.8 | 279.7 | 178.3 | 0.40 |
| | | | | | | | |
| 2 | Middle | 368.4 | 486.8 | 326.5 | 291.9 | 177.6 | 0.29 |
| 3 | | 373.7 | 538.5 | 311.4 | 271.1 | 247.3 | 0.24 |
| 4 | | 376.1 | 534.0 | 316.0 | 278.4 | 236.7 | 0.24 |
| | | | | | | | |
| H8P6O19 | 1 | Endgroup | 366.6 | 492.1 | 321.8 | 285.9 | 188.2 | 0.29 |
| 6 | | 368.1 | 516.8 | 318.4 | 268.9 | 223.2 | 0.33 |
| | | | | | | | |
| 5 | Middle | 376.7 | 548.3 | 304.8 | 277.2 | 257.3 | 0.16 |
| 3 | | 377.3 | 540.4 | 311.7 | 279.7 | 244.7 | 0.20 |
| 2 | | 378.8 | 501.1 | 336.6 | 298.6 | 183.5 | 0.31 |
| 4 | | 379.1 | 534.6 | 326.9 | 275.8 | 233.3 | 0.33 |
The
ab initio NMR simulations of the
31P CSA tensor for the 2-,3- and 4- P membered phosphate rings are given in
Table 2. The simulated
31P CSA tensors for the different 5-P membered and 6-P membered cyclic clusters are given in
Table 3 and
Table 4, respectively. These simulations also show a wide distribution of both the chemical shift and the anisotropy as a function of the number of phosphate tetrahedra in the cluster. Even for the cyclic phosphate clusters with constant number of phosphate tetrahedra, there are differences in the
31P CSA tensor produced by the different conformations being investigated. Again these variations probably result from the combined effect of both P-O-P bond angle and O
b-P-O
b / P-O
t torsional angle variations.
The effects of cyclization for the smaller clusters are similar to previous calculations in phosphate systems. There is a +4 to +20 ppm increase in the chemical shielding noted for the phosphates between the cyclic H
3P
3O
9 (both conformations) and the middle phosphate species in the H
5P
3O
10 cluster (
Table 1 and
Table 2).
Ab initio calculations of the P
3O
105- and the cyclic P
3O
93- Na-P species predicted a similar +7.1 ppm increase in the
31P chemical shielding [
7]. The isotropic chemical shielding for the H
2P
2O
6 cluster (
Table 2) is not distinctly different from the other cyclic phosphate
Table 2.
Ab Initio NMR 31P CSA Tensors for Cyclic 2-, 3- and 4-P Membered Phosphate Clusters.
Table 2.
Ab Initio NMR 31P CSA Tensors for Cyclic 2-, 3- and 4-P Membered Phosphate Clusters.
| Cluster | IDa | Conformation | σiso(ppm) | σ33(ppm) | σ22(ppm) | σ11(ppm) | Δσ(ppm) | η |
| H2P2O6 | 1 | (+ +) | 373.8 | 574.7 | 278.3 | 268.3 | 301.4 | 0.05 |
| 2 | | 381.2 | 599.9 | 281.7 | 262.1 | 328.0 | 0.09 |
| | | | | | | | |
| 1 | (− +) | 379.1 | 591.4 | 284.0 | 261.9 | 318.5 | 0.10 |
| 2 | | 379.1 | 591.4 | 284.0 | 261.9 | 318.5 | 0.10 |
| | | | | | | | |
| H3P3O9 | 1 | (+ + +) | 386.9 | 583.4 | 293.0 | 284.3 | 294.8 | 0.04 |
| 2 | | 386.9 | 583.4 | 293.0 | 284.3 | 294.8 | 0.04 |
| 3 | | 387.0 | 583.6 | 293.0 | 284.4 | 294.9 | 0.04 |
| | | | | | | | |
| 3 | (+ + −) | 370.4 | 511.2 | 316.1 | 284.0 | 211.2 | 0.22 |
| 1 | | 387.5 | 587.2 | 293.7 | 281.4 | 299.7 | 0.06 |
| 2 | | 387.5 | 587.2 | 293.7 | 281.4 | 299.7 | 0.06 |
| | | | | | | | |
| H4P4O12 | 1 | (+ + + +) | 381.8 | 544.6 | 307.1 | 293.6 | 244.3 | 0.08 |
| 2 | | 381.8 | 544.6 | 307.1 | 293.6 | 244.3 | 0.08 |
| 3 | | 384.8 | 555.5 | 302.7 | 296.3 | 256.0 | 0.04 |
| 4 | | 384.8 | 555.5 | 302.7 | 296.3 | 256.0 | 0.04 |
| | | | | | | | |
| 3 | (+ + + −) | 379.0 | 532.7 | 311.9 | 292.5 | 230.5 | 0.13 |
| 1 | | 379.8 | 522.5 | 326.3 | 290.4 | 214.2 | 0.25 |
| 2 | | 383.3 | 555.5 | 298.3 | 296.2 | 258.3 | 0.01 |
| 4 | | 386.2 | 580.8 | 298.5 | 279.4 | 291.9 | 0.10 |
| | | | | | | | |
| 1 | (+ + − −) | 391.6 | 563.1 | 312.0 | 299.7 | 257.3 | 0.07 |
| 2 | | 391.6 | 563.1 | 312.0 | 299.7 | 257.3 | 0.07 |
| 3 | | 391.6 | 563.1 | 312.0 | 299.7 | 257.3 | 0.07 |
| 4 | | 391.6 | 563.1 | 312.0 | 299.7 | 257.3 | 0.07 |
| | | | | | | | |
| 1 | (+ −+ −) | 375.8 | 512.1 | 320.7 | 294.6 | 204.4 | 0.19 |
| 2 | | 375.9 | 517.4 | 317.8 | 292.4 | 212.3 | 0.18 |
| 3 | | 386.7 | 578.4 | 300.9 | 280.9 | 287.5 | 0.10 |
| 4 | | 390.0 | 584.6 | 304.8 | 280.7 | 291.9 | 0.12 |
clusters reported in this study. In contrast the shielding anisotropy (Δσ) is nearly 50 to 100 ppm larger than any of the other phosphate clusters reported. This large tensor anisotropy results from the very strained ring structure, where the P-O-P bond angle (within the ring plane) is only 94
o and 95
o for the
cis and
trans configuration, respectively. The internal O-P-O bond angles are also highly distorted, being approximately 85
o. For the H
3P
3O
9 clusters (
Figure 2) the structural distortions are less severe, but the P-O-P bond angles still range between 121
o and 139
o; smaller than the average P-O-P bond angle observed in the acyclic and larger cyclic phosphate clusters. For the H
4P
4O
12, H
5P
5O
15 and H
6P
6O
18 clusters (
Figure 2 and
Figure 3) the P-O-P bond angles range from 129
o to 150
o. For these larger cyclic phosphate clusters the observed range of isotropic chemical shielding is very broad ranging from +370
Table 3.
Ab Initio NMR CSA Tensors for Cyclic 5-P Membered Phosphate Clusters.
Table 3.
Ab Initio NMR CSA Tensors for Cyclic 5-P Membered Phosphate Clusters.
| Cluster | IDa | Conformation | σiso(ppm) | σ33(ppm) | σ22(ppm) | σ11(ppm) | Δσ(ppm) | η |
| H5P5O15 | 5 | (+ + + + +) | 382.0 | 543.1 | 310.8 | 292.0 | 241.7 | 0.12 |
| 3 | | 382.2 | 552.4 | 304.1 | 290.2 | 255.2 | 0.08 |
| 2 | | 383.3 | 548.3 | 308.4 | 293.4 | 247.4 | 0.09 |
| 1 | | 384.3 | 556.2 | 299.5 | 297.2 | 257.8 | 0.01 |
| 4 | | 385.4 | 560.0 | 302.5 | 293.8 | 261.8 | 0.05 |
| | | | | | | | |
| 3 | (+ + + + −) | 375.9 | 515.8 | 320.1 | 291.8 | 209.9 | 0.20 |
| 5 | | 381.4 | 561.6 | 303.3 | 279.4 | 270.3 | 0.13 |
| 1 | | 383.7 | 554.9 | 299.8 | 296.3 | 256.9 | 0.02 |
| 2 | | 384.3 | 546.7 | 312.3 | 294.0 | 243.6 | 0.11 |
| 4 | | 388.6 | 564.7 | 302.6 | 298.4 | 264.3 | 0.02 |
| | | | | | | | |
| 3 | (+ + + − −) | 376.1 | 519.8 | 317.9 | 290.7 | 215.5 | 0.19 |
| 5 | | 381.1 | 561.7 | 303.2 | 278.3 | 270.9 | 0.14 |
| 1 | | 383.8 | 551.2 | 305.5 | 294.9 | 251.0 | 0.06 |
| 2 | | 385.1 | 546.9 | 311.7 | 296.6 | 242.8 | 0.09 |
| 4 | | 387.7 | 563.9 | 301.2 | 298.1 | 264.3 | 0.02 |
| | | | | | | | |
| 3 | (+ + − + −) | 375.2 | 515.5 | 318.8 | 291.2 | 210.5 | 0.20 |
| 1 | | 377.9 | 518.7 | 323.4 | 291.7 | 211.2 | 0.23 |
| 2 | | 379.8 | 532.8 | 320.8 | 285.7 | 229.6 | 0.23 |
| 5 | | 381.6 | 563.8 | 301.7 | 279.5 | 273.2 | 0.12 |
| 4 | | 388.7 | 585.3 | 302.7 | 278.1 | 294.9 | 0.13 |
ppm to nearly +395 ppm (
Table 2,
Table 3 and
Table 4). There does not appear to be any simple correlation between cluster ring size and tensor values (except for the highly strained H
2P
2O
6 cluster). Correlations between the isotropic shielding, the shielding anisotropy and the cluster size are discussed later in this section.
The absolute isotropic chemical shielding values (σ
iso) presented in
Table 1,
Table 2,
Table 3 and
Table 4 can be converted to chemical shifts (δ) relative to 85% H
3PO
4 by comparison to the chemical shielding of PH
3 at the same level of theory using [
11]
This relationship is based on the experimental chemical shift of PH
3 (δ = 266.1 ppm). The shielding for PH
3 at this level of theory has already been reported as 590.1 ppm [
5].
The asymmetry of the CSA tensor (η) is also variable (see
Table 1,
Table 2,
Table 3 and
Table 4), ranging from 0.01 (a symmetric environment) to 0.40. The smaller or highly symmetric clusters commonly show symmetric
31P CSA tensors. For example, the (+ + + +), and the (+ + − −) conformations in the H
4P
4O
12 clusters are predicted to have very small η values. In general, there does not appear to be any
Table 4.
Ab Initio NMR CSA Tensors for Cyclic 6-P Membered Phosphate Clusters.
Table 4.
Ab Initio NMR CSA Tensors for Cyclic 6-P Membered Phosphate Clusters.
| Cluster | IDa | Conformation | σiso(ppm) | σ33(ppm) | σ22(ppm) | σ11(ppm) | Δσ(ppm) | η |
| H6P6O18 | 5 | (+ + + + + +) | 378.4 | 543.1 | 305.6 | 286.4 | 247.1 | 0.12 |
| 6 | | 384.0 | 546.4 | 313.9 | 291.7 | 243.6 | 0.14 |
| 1 | | 385.5 | 564.6 | 307.8 | 284.1 | 268.6 | 0.13 |
| 4 | | 387.7 | 567.0 | 306.7 | 289.3 | 269.0 | 0.10 |
| 2 | | 389.8 | 579.1 | 303.3 | 287.1 | 284.0 | 0.09 |
| 3 | | 390.6 | 578.8 | 308.0 | 285.1 | 282.3 | 0.12 |
| | | | | | | | |
| 6 | (+ + + + + −) | 377.4 | 487.8 | 334.7 | 309.7 | 165.6 | 0.25 |
| 5 | | 379.3 | 534.8 | 313.0 | 289.9 | 233.3 | 0.15 |
| 1 | | 383.7 | 566.5 | 302.4 | 282.4 | 274.1 | 0.11 |
| 2 | | 387.8 | 574.9 | 307.2 | 281.3 | 280.6 | 0.14 |
| 3 | | 388.5 | 576.9 | 303.1 | 285.4 | 282.7 | 0.09 |
| 4 | | 388.9 | 567.0 | 308.4 | 291.3 | 267.1 | 0.10 |
| | | | | | | | |
| 5 | (+ + + − − −) | 380.1 | 492.5 | 341.6 | 306.2 | 168.5 | 0.31 |
| 1 | | 383.2 | 565.3 | 303.9 | 280.3 | 273.3 | 0.13 |
| 6 | | 383.9 | 509.7 | 336.1 | 305.9 | 188.7 | 0.24 |
| 3 | | 385.4 | 561.8 | 307.7 | 286.8 | 264.6 | 0.12 |
| 2 | | 387.5 | 577.2 | 305.9 | 279.5 | 284.5 | 0.14 |
| 4 | | 394.9 | 587.4 | 308.8 | 288.5 | 288.8 | 0.11 |
| | | | | | | | |
| 6 | (+ + + + − −) | 378.0 | 488.5 | 341.2 | 304.3 | 165.8 | 0.33 |
| 5 | | 382.0 | 508.5 | 332.4 | 305.2 | 189.7 | 0.22 |
| 1 | | 382.3 | 564.0 | 303.1 | 279.9 | 272.5 | 0.13 |
| 3 | | 386.7 | 561.7 | 311.2 | 287.1 | 262.6 | 0.14 |
| 2 | | 390.0 | 579.9 | 306.7 | 283.5 | 284.8 | 0.12 |
| 4 | | 390.1 | 581.5 | 309.5 | 279.2 | 287.1 | 0.16 |
| | | | | | | | |
| 3 | (+ − + − − − ) | 371.5 | 507.0 | 322.5 | 284.9 | 203.3 | 0.28 |
| 6 | | 374.3 | 477.4 | 332.3 | 313.4 | 154.5 | 0.18 |
| 5 | | 379.9 | 546.8 | 304.7 | 288.3 | 250.3 | 0.10 |
| 2 | | 381.3 | 553.7 | 314.0 | 276.2 | 258.6 | 0.22 |
| 1 | | 384.7 | 565.6 | 305.5 | 283.0 | 271.3 | 0.12 |
| 4 | | 388.8 | 586.7 | 298.0 | 281.7 | 296.8 | 0.08 |
| | | | | | | | |
| 3 | (+ − + − + − ) | 370.2 | 503.7 | 322.6 | 284.3 | 200.3 | 0.29 |
| 6 | | 375.2 | 481.6 | 331.3 | 312.7 | 159.6 | 0.17 |
| 2 | | 380.3 | 549.5 | 315.7 | 275.7 | 253.8 | 0.24 |
| 5 | | 380.6 | 550.5 | 305.5 | 285.7 | 254.9 | 0.12 |
| 1 | | 383.7 | 565.1 | 302.7 | 283.4 | 272.1 | 0.11 |
| 4 | | 388.2 | 585.5 | 298.0 | 281.2 | 295.9 | 0.09 |
absolute correlation between η and the size of the cluster, or whether the cluster was cyclic or acyclic. For the cyclic phosphate clusters it was noted that the phosphate species with larger η typically had smaller Δσ, but this trend is not universal, and does not extend to the acyclic phosphate clusters investigated (see
Table 2,
Table 3 and
Table 4).
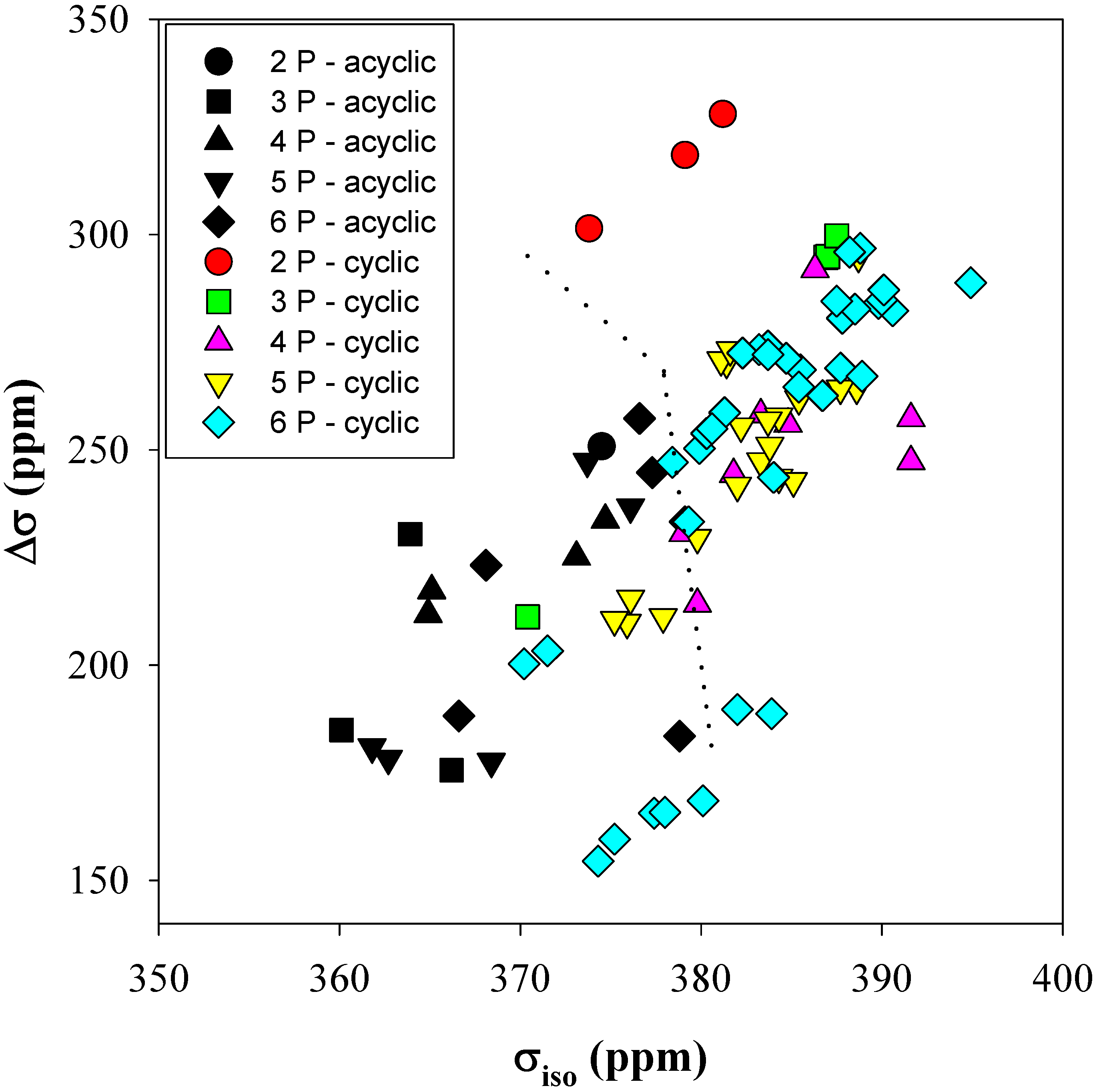
Figure 4 shows the correlation between the
31P isotropic chemical shielding (σ
iso) and the CSA anisotropy (Δσ) as a function of the number of phosphates in the both acyclic and cyclic clusters. There are regions were distinct differences between the
31P CSA tensors for cyclic and acyclic clusters are observed: most notably for the 2-P, 3-P and 4-P-membered phosphate rings. The dotted lines in
Figure 4 are for visual separation of these regions. For cyclic clusters Δσ is typically greater than ~ +250 ppm, with σ
iso being larger than ~ +375 ppm. The acyclic clusters tend to have smaller tensor values than cyclics, with values of +250 ppm and +375 ppm for Δσ and σ
iso, respectively. This distinction between cyclic and acyclic phosphate clusters disappears for the 5-P and 6-P-membered rings, where overlap between the predicted cyclic and acyclic
31P CSA parameters was observed. This loss of distinct differences in the larger cyclic clusters was expected since these are 10- and 12-membered rings (P and O) where the possible ring conformations do not require as many restrictive structural constraints. It is interesting to note that the highly strained 2-P-membered ring conformations [
8] have a larger anisotropy (~ +325 ppm) than any of the other cyclic clusters, as was discussed earlier in this section.
Figure 4.
The calculated 31P CSA isotropic chemical shielding (σiso) versus shielding anisotropy (Δσ) for different sized acyclic and cyclic phosphate clusters.
Figure 4.
The calculated 31P CSA isotropic chemical shielding (σiso) versus shielding anisotropy (Δσ) for different sized acyclic and cyclic phosphate clusters.
Effect of Cyclization on Orientation of CSA Tensor
In general the chemical shielding tensor contains both symmetric and antisymmetric components. The antisymmetric components of the shielding tensor, as well as other non-secular components, contribute only in second order to the observed frequency, and can be readily neglected [
17]. The GAUSSIAN 98 output contains both the symmetric and antisymmetric tensor components. To determine the relative orientation of the CSA tensor, it is therefore necessary to decompose the
31P CSA tensor (
) into the symmetric (
), and antisymmetric (
) components [
18]
The antisymmetric components of
are given by
where
is the transpose. The symmetric component
is therefore the only part of concern, and is diagonal in the PAS, with the eigenvalues of this diagonal representation being used in description of the
31P CSA tensor through Equations 1- 4.
The relative orientation of the CSA tensor in the PAS and the tensor orientation in the molecular coordinate system allows additional changes in the tensor due to cyclization to be addressed. The representation of the CSA tensor (symmetric portion only) in the PAS is diagonal and will be denoted by
. The matrix representation of the CSA tensor in a different coordinate system (
), in this case the molecular frame representation given by GAUSSIAN 98, can be realized by a transformation between the two coordinate systems according to [
18]
where
RD is the rotation matrix. This can be reduced to a principal-value relationship
where σ
n are the eigenvalues of the matrix
, and the eigenvectors
are the column vectors of the rotation matrix
RD. These eigenvectors describe the orientation of the PAS in the molecular coordinate axis system. A more detailed description of these transformations is given in Reference [
18].
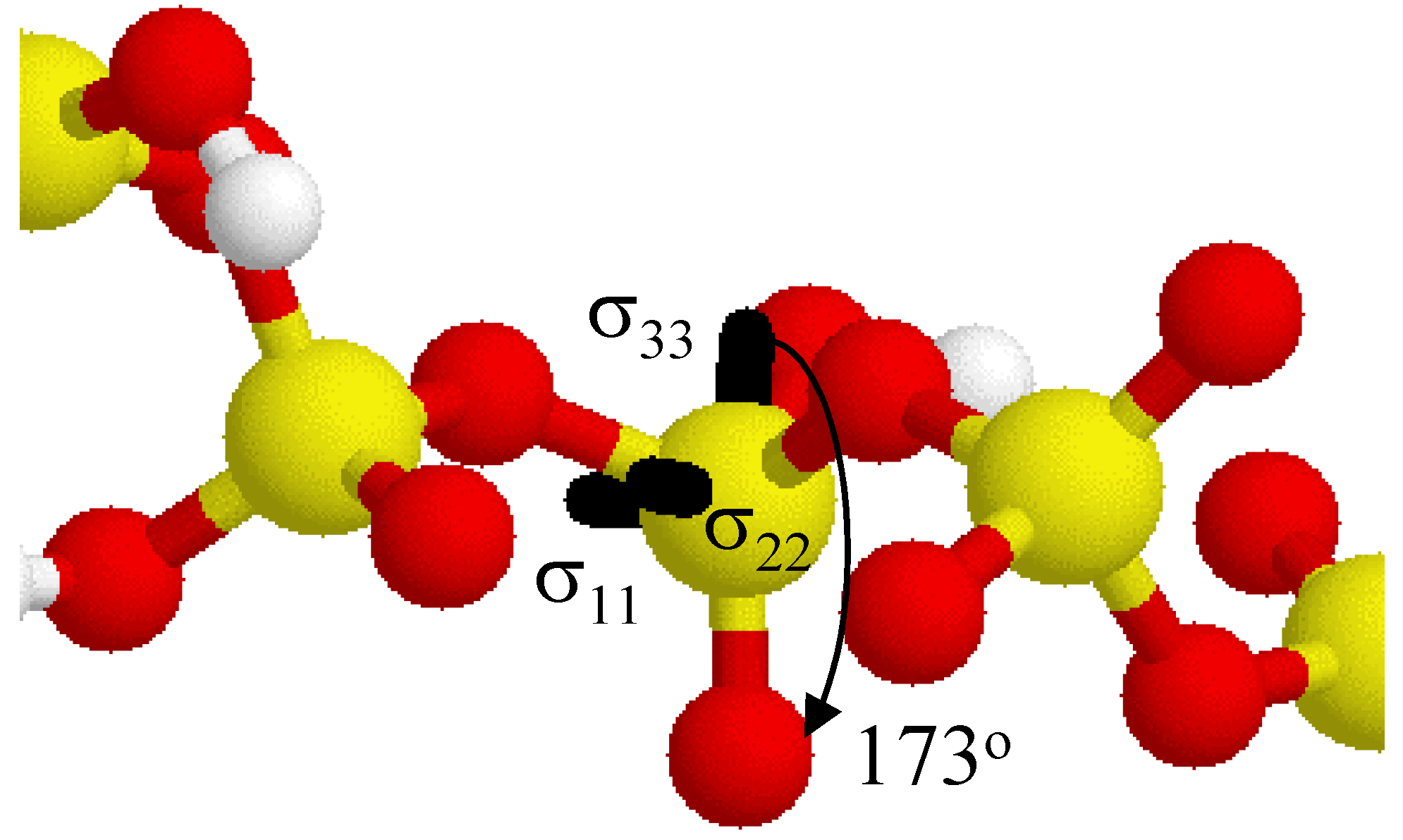
Figure 5 shows the relative orientation of the
31P CSA tensor in the acyclic 5-P-member cluster. Only the central portion of the acyclic phosphate cluster is shown for clarity. The largest principal component σ
33 is oriented approximately 173
o from the terminal P=O bond axis (nearly collinear).
Figure 5.
Relative orientation of the 31P CSA tensor for the central phosphate in the acyclic 5-P-membered cluster. The σ33 principal component lies ~ 173o from the terminal P=O bond. Some intervening hydrogen atoms have been removed for clarity.
Figure 5.
Relative orientation of the 31P CSA tensor for the central phosphate in the acyclic 5-P-membered cluster. The σ33 principal component lies ~ 173o from the terminal P=O bond. Some intervening hydrogen atoms have been removed for clarity.
Both the σ11 and σ22 tensor elements split the P-O-P bond projection, and are not collinear with either the P-OH or the P-O-P bonds. In general, due to the lack of bonding symmetry only the σ33 element is approximately collinear with any of the P-O bonds in these clusters.
The relative orientation of the
31P CSA tensor for the 2-P-membered
cis (+ +) and
trans (+ −) cyclic cluster is shown in
Figure 6. For both the
cis and
trans cluster the σ
33 principal component is nearly parallel to the terminal P=O bond vector (~12
o-13
o), while the projection of the σ
22 component bisects the two P-O-P bonds forming the ring, and the σ
11 component lies in the plane of the 2-P-membered ring. The orientation of the σ
22 tensor element between the two bridging oxygen atoms forming the ring is consistent with the high anisotropy observed for these smaller cyclic clusters (see
Table 2 and
Figure 2). The largest principal component σ
33 is still approximately along the terminal P=O bond.
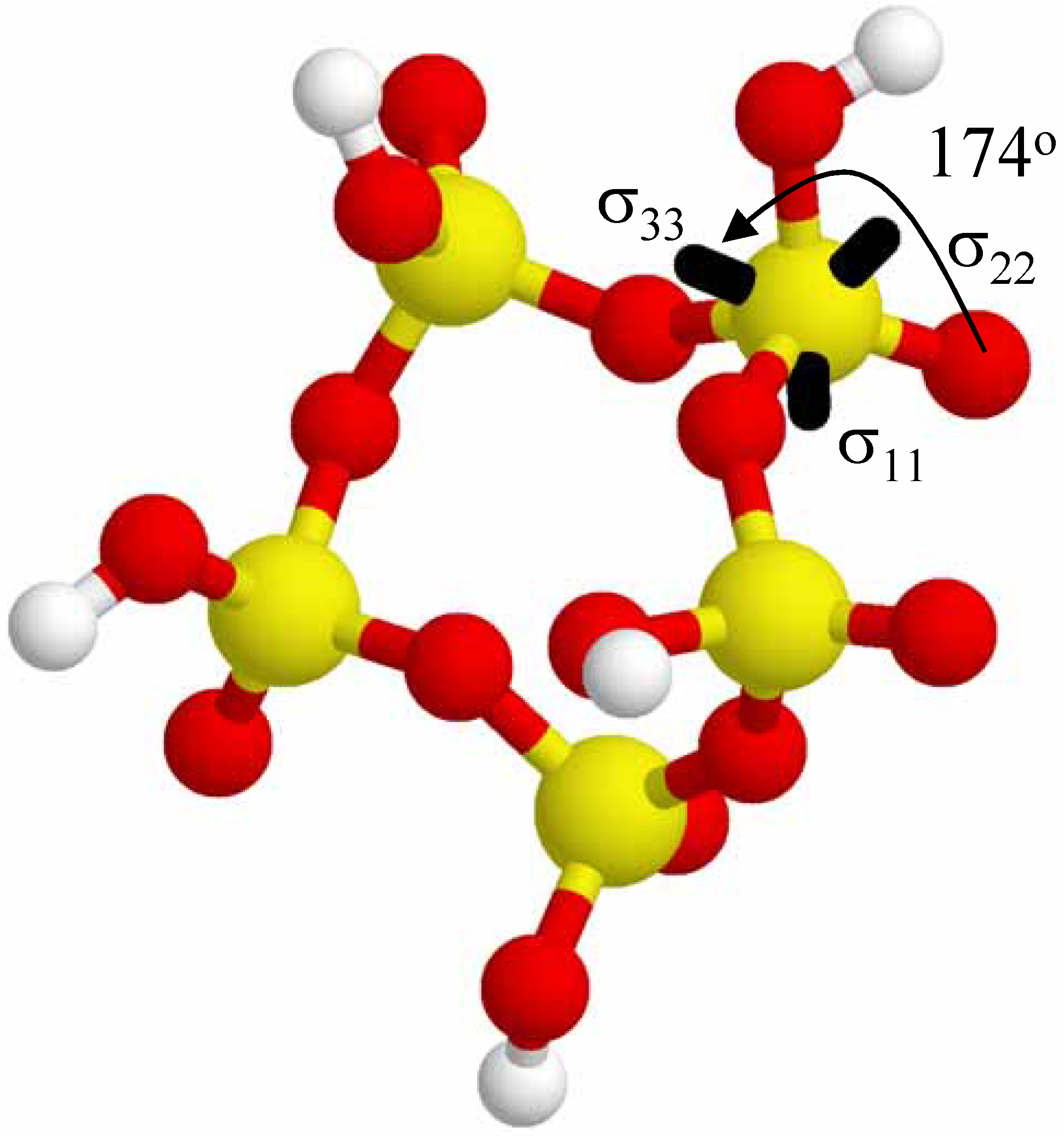
Figure 7 shows the orientation of the
31P CSA tensor for a single phosphate tetrahedral (σ
iso = 383.3 ppm, ID #2, see
Table 3) in the (+ + + + +) 5-P-membered cyclic cluster. There are slightly different orientations of the CSA tensor depending on which specific phosphate is being investigated, but this single example is illustrative of the tensor orientations observed in the larger cyclic clusters. The σ
33 principal component is approximately 174
o from the terminal P=O direction (or about 6
o from the P=O axis), with the σ
11 and σ
22 tensor elements not being collinear with either the P-OH or the P-O-P bonds. These results are similar to the results seen in the larger acyclic clusters (See
Figure 5), as well as the 2-P membered cyclic clusters (
Figure 6). For the 2-P membered cyclics the small asymmetry parameter means that σ
11 and σ
22 are very similar, but are defined through Equation 4. Reversal of the σ
11 and σ
22 principal components would result in the σ
33 tensor element being pointed in the same general direction as the σ
33 tensor elements in
Figure 5 and
Figure 7.
Figure 6.
The relative orientation of the 31P CSA tensor in the cis (+ +) and the trans (+ −) configurations in the 2-P-membered cyclic phosphate clusters. The orientation of the tensor is nearly identical in both configurations, with the σ33 principal axis being ~12o from the terminal P=O bond.
Figure 6.
The relative orientation of the 31P CSA tensor in the cis (+ +) and the trans (+ −) configurations in the 2-P-membered cyclic phosphate clusters. The orientation of the tensor is nearly identical in both configurations, with the σ33 principal axis being ~12o from the terminal P=O bond.
Figure 7.
The relative orientation of the 31P CSA tensor (only one specific phosphate shown for clarity) in the (+ + + + +) 5-P-membered cyclic cluster. The σ33 principal component lies ~ 174o from the direction of the terminal P=O bond.
Figure 7.
The relative orientation of the 31P CSA tensor (only one specific phosphate shown for clarity) in the (+ + + + +) 5-P-membered cyclic cluster. The σ33 principal component lies ~ 174o from the direction of the terminal P=O bond.