Coupled Cluster Calculations of the Ground and Excited Electronic States Using Two- and Four-Component Relativistic Spinors
Abstract
:1 Introduction
2 Coupled Cluster Based Linear Response Theory
 , and the corresponding energy ωk are obtained from an equation of the form [2,3,4,5,6,7]:
, and the corresponding energy ωk are obtained from an equation of the form [2,3,4,5,6,7]:

 are expressed as a linear combination of various spin-free hole-particle excitations operators, written in normal-order. Thus, for example, for single and double excitations, one has operators like
are expressed as a linear combination of various spin-free hole-particle excitations operators, written in normal-order. Thus, for example, for single and double excitations, one has operators like


 are expressed as
are expressed as


 s for ionization and electron attach-ment processes are expressed as
s for ionization and electron attach-ment processes are expressed as


 commute, premultiplying eq. (2) by exp(−T) we get the following equation of motion (EOM):
commute, premultiplying eq. (2) by exp(−T) we get the following equation of motion (EOM):


 , we get
, we get

 and the associated matrix A.
and the associated matrix A.3 Results
 where the excitation/ionization operator
where the excitation/ionization operator  is truncated at 2h-2p level for EE, 2h-1p for IP, and 1h-2p for EA processes, respectively. To avoid variational collapse in the DF procedure, we impose kinetic balance condition and relativistic boundary conditions on the basis spinors. Since the expression for kinetic balance condition is simple for uncontracted Gaussian/Slater functions, we use uncontracted Gaussian basis to gener-ate the Hartree-Fock(HF), RESC and Dirac-Fock (DF)orbitals. While the HF and RESC orbitals are obtained from GAMESS [11] code, the DF orbitals are generated from the code developed in our laboratory. Note that in the present RESC scheme, only the one electron integral corrections are added. A more accurate treatment can be achieved by means of relativistically averaged basis set which incorporates the two- electron integral corrections. However, the RESC corrections to two-electron is beyond the scope of the present work.
is truncated at 2h-2p level for EE, 2h-1p for IP, and 1h-2p for EA processes, respectively. To avoid variational collapse in the DF procedure, we impose kinetic balance condition and relativistic boundary conditions on the basis spinors. Since the expression for kinetic balance condition is simple for uncontracted Gaussian/Slater functions, we use uncontracted Gaussian basis to gener-ate the Hartree-Fock(HF), RESC and Dirac-Fock (DF)orbitals. While the HF and RESC orbitals are obtained from GAMESS [11] code, the DF orbitals are generated from the code developed in our laboratory. Note that in the present RESC scheme, only the one electron integral corrections are added. A more accurate treatment can be achieved by means of relativistically averaged basis set which incorporates the two- electron integral corrections. However, the RESC corrections to two-electron is beyond the scope of the present work. and
and  versus the atomic number. The present work shows that the ground energy obtained from HF orbital is less than that obtained from the RESC and DF orbitals. Figure 1 also demonstrates that while
versus the atomic number. The present work shows that the ground energy obtained from HF orbital is less than that obtained from the RESC and DF orbitals. Figure 1 also demonstrates that while  increases with increasing atomic number,
increases with increasing atomic number,  remains quite close to
remains quite close to  over the entire range. The fact that
over the entire range. The fact that  for the ground state clearly demonstrates that dominant relativistic corrections can be incorporated through RESC scheme.
for the ground state clearly demonstrates that dominant relativistic corrections can be incorporated through RESC scheme.| System | Basis set | Ref. |
| Be | 16s9p5d1f | [15] |
| B | 16s10p5d1f | [15] |
| C | 14s10p4d1f | [15] |
| Ne | 13s9p5d2f | [16] |
| Ar | 20s13p4d2f | [17] |
| Rb | 15s12p8d2f | [18] |
| Cs | 15s12p8d2f | [18] |
 (solid line) and
(solid line) and  (dotted line) versus the atomic number (Z).
(dotted line) versus the atomic number (Z).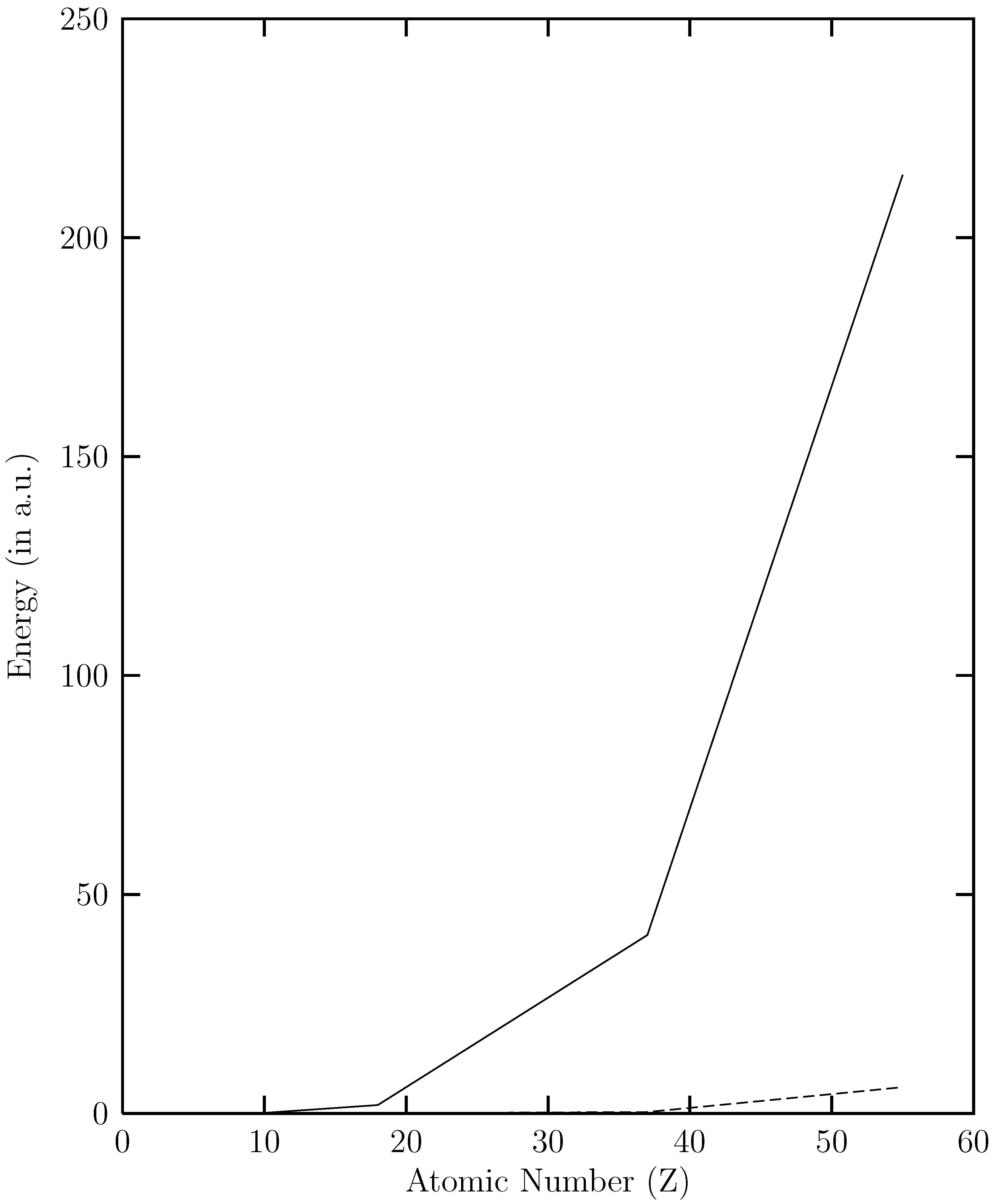
| System | CCLRT | Experiment [12] | ||
| HF | RESC | DF | ||
| Be | 9.315 | 9.316 | 9.322 | 9.322 |
| B | 8.222 | 8.220 | 8.223 | 8.298 |
| B+ | 25.134 | 25.140 | 25.146 | 25.155 |
| C+ | 24.292 | 24.289 | 24.289 | 24.383 |
| Ne | 21.240 | 21.262 | 21.633 | 21.564 |
| Ar | 15.656 | 15.638 | 15.898 | 15.759 |
| Rb | 4.074 | 4.141 | 4.185 | 4.177 |
| Cs | 3.735 | 3.889 | 3.960 | 3.894 |
| Average Error | 1.269% | 0.576% | 0.552% | |
| System | Dominant | CCLRT | Experiment [12] | ||
| Configuration | HF | RESC | DF | ||
| B | [Be]2p(2P3/2) | 66322 | 66946 | ||
| [Be]3s(2S1/2) | 26787 | 26790 | 26723 | 26890 | |
| [Be]4s(2S1/2) | 11829 | 11830 | 11789 | 11921 | |
| C+ | [Be]2p(2P3/2) | 195903 | 196723 | ||
| [Be]3p(2P1/2) | 64551 | 64934 | |||
| [Be]3p(2P3/2) | 64786 | 64783 | 64780 | 64923 | |
| Rb | [Kr]6s(2S1/2) | 10963 | 11242 | 11260 | 13557 |
| [Kr]5p(2P1/2) | 20804 | 21112 | |||
| [Kr]5p(2P3/2) | 20481 | 20500 | 20577 | 20874 | |
| Cs | [Xe]7s(2S1/2) | 9067 | 9854 | 9960 | 12872 |
| [Xe]6p(2P1/2) | 19741 | 20229 | |||
| [Xe]6p(2P3/2) | 19215 | 19265 | 19309 | 19674 | |
| Average Error | 7.754% | 6.534% | 6.397% | ||
4 Discussion
| System | Dominant | CCLRT | Experiment [12] | |
| Configuration | HF | RESC | ||
| Be | [He]2s3s(1S) | 54657 | 54665 | 54662 |
| [He]2s2p(1P ) | 42806 | 42819 | 42565 | |
| [He]2s3p(1P ) | 60418 | 60429 | 60187 | |
| [He]2s4s(1S) | 65222 | 65230 | 65245 | |
| [He]2s5s(1S) | 70107 | 70115 | 69332 | |
| B+ | [He] 2s2p(1P ) | 73993 | 74052 | 73397 |
| [He] 2p2(1D) | 104338 | 104449 | 102362 | |
| [He] 2p2(1S) | 129283 | 129368 | 127622 | |
| [He] 2s3s(1S) | 138333 | 138396 | 137622 | |
| [He] 2s3p(1P ) | 144079 | 144131 | 144103 | |
| [He] 2p2(1D) | 156856 | 156907 | 154687 | |
| [He] 2s4s(1S) | 167801 | 167845 | 167936 | |
| [He] 2s4p(1P ) | 171322 | 171374 | 170591 | |
| C++ | [He] 2s2p(1P ) | 103254 | 103411 | 102351 |
| [He] 2p2(1D) | 148668 | 148966 | 145875 | |
| [He] 2s3s(1S) | 185593 | 185883 | 182520 | |
| Average Error | 0.82% | 0.87% | ||
References
- Nakajima, T.; Suzumura, T.; Hirao, K. Chem. Phys. Letts. 1999, 304, 271.Suzumura, T.; Nakajima, T.; Hirao, K. Int. J. Quantum Chem. 1999, 75, 757. [CrossRef]Nakajima, T.; Koga, K.; Hirao, H. J. Chem. Phys. 2001, 112, 10142.Motegi, K.; Nakajima, T.; Hirao, K.; Seijo, L. J. Chem. Phys. 2001, 114, 6000.
- Mukherjee, D.; Mukherjee, P.K. Chem. Phys. 1979, 37, 327.
- Ghosh, S.; Bhattacharyya, S.N.; Mukherjee, D. Chem. Phys. 1982, 72, 961.
- Adnan, S.S.Z.; Bhattacharyya, S.N.; Mukherjee, D. Mol. Phys. 1982, 39, 519.
- Adnan, S.S.Z.; Bhattacharyya, S.N.; Mukherjee, D. Chem. Phys. Letts. 1982, 85, 204.
- Mukhopadhayay, S.; Chaudhuri, R.K.; Mukhopadhyay, D.; Mukherjee, D. Chem. Phys. Letts. 1990, 173, 181.
- Kundu, B.; Mukherjee, D. Chem. Phys. Letts. 1991, 179, 468. [CrossRef]
- Monkhorst, H.J. Int. J. Quantum Chem. 1977, S11, 421.Dalgaard, E.; Monkhorst, H.J. Phys. Rev. 1983, A 28, 1217. [CrossRef]
- Sekino, H.; Bartlett, R.J. Int. J. Quantum Chem. 1984, S 18, 255. [CrossRef]Greetsen, J.; Rittby, M.; Bartlett, R.J. Chem. Phys. Lett. 1989, 164, 57.
- Koch, H.; Jensen, H.J.A.; Jorgensen, P.; Helgaker, T. J. Chem. Phys. 1990, 93, 3345.Koch, H.; Jorgensen, P. J. Chem. Phys. 1990, 93, 3333.
- Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.H.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.J.; Windus, T.L.; Dupuis, M.; Montgomery, J.A. J. Comput. Chem. 1993, 14, 1347. [CrossRef]
- Moore, C.E. Atomic Energy Levels. In Natl. Bur. Standard, Ref. Data Ser., Natl. Bur. Stand.; (U.S.) Circ. No. 35; U.S. GPO: Washington, D. C., 1971; Vol 1. [Google Scholar]
- Chaudhuri, R.K.; Sahoo, B.K.; Das, B.P.; Merlitz, H.; Mahapatra, U.S.; Mukherjee, D. J. Chem. Phys. (in press).
- Nayak, M.K.; Chaudhuri, R.K. (to be submitted).
- Maroulis, G.; Bishop, D.M. J. Phys. B 1985, 18, 3653. [CrossRef]
- Maroulis, G.; Bishop, D.M. Chem. Phys. Letts. 1985, 114, 182. [CrossRef]
- Schmidt, M.W.; Ruedenberg, K. J. Chem. Phys. 1979, 71, 3951. Exponents for the Ar polarization functions are constructed from their p exponents.
- Godbout, N.; Salahub, D.R.; Andzelm, J.; Wimmer, E. Can. J. Chem. 1992, 70, 560. Rb basis is generated by adding exponents to Godbout et al. basis set. The same basis set is used for Cs atom.
©2003 by MDPI, Basel, Switzerland. Reproduction for noncommercial purposes permitted.
Share and Cite
Chaudhuri, R.K. Coupled Cluster Calculations of the Ground and Excited Electronic States Using Two- and Four-Component Relativistic Spinors. Int. J. Mol. Sci. 2003, 4, 586-594. https://0-doi-org.brum.beds.ac.uk/10.3390/i4120586
Chaudhuri RK. Coupled Cluster Calculations of the Ground and Excited Electronic States Using Two- and Four-Component Relativistic Spinors. International Journal of Molecular Sciences. 2003; 4(12):586-594. https://0-doi-org.brum.beds.ac.uk/10.3390/i4120586
Chicago/Turabian StyleChaudhuri, Rajat K. 2003. "Coupled Cluster Calculations of the Ground and Excited Electronic States Using Two- and Four-Component Relativistic Spinors" International Journal of Molecular Sciences 4, no. 12: 586-594. https://0-doi-org.brum.beds.ac.uk/10.3390/i4120586




