The Spin–Spin Coupling Constants in Ethane, Methanol and Methylamine: A Comparison of DFT, MCSCF and CCSD Results
Abstract
:1 Introduction
2 Computational details
3 Results and discussion
3.1 One-bond coupling constants
| DFT | RASSCF | CCSD | exp. | ||
| CH3CH3 | 1J(CH) | 122.6 | 120.3 | 114.1 | 125.19 – 125.238 |
| CH3NH2 | 1J(CH) | 129.5 | 128.3 | 120.9 | 132.2 (0.2) |
| CH3OH | 1J(CH) | 135.1 | 134.2 | 126.3 | 141 |
| CH3NH2 | 1J(NH) | −63.3 | −65.0 | −61.7 | −65.0 (0.2) |
| CH3OH | 1J(OH) | −68.7 | −78.5 | −75.9 | −85 (10) |
| CH3CH3 | 1J(CC) | 32.6 | 38.4 | 34.1 | 34.498 – 34.558 |
| CH3NH2 | 1J(CN) | −2.3 | −6.5 | −5.1 | −4.5 (0.5) |
| CH3OH | 1J(CO) | 19.9 | 11.1 | 12.4 | – |
| Fermi contact | Spin-dipole | Paramagnetic SO | Diamagnetic SO | ||||||||||
| DFT | RAS | CCSD | DFT | RAS | CCSD | DFT | RAS | CCSD | DFT | RAS | CCSD | ||
| CH3CH3 | 1J(CH) | 120.9 | 118.9 | 112.6 | −0.1 | −0.2 | −0.2 | 1.3 | 1.2 | 1.2 | 0.5 | 0.5 | 0.5 |
| CH3NH2 | 1J(CH) | 128.3 | 127.3 | 119.9 | −0.1 | −0.3 | −0.2 | 0.8 | 0.7 | 0.7 | 0.5 | 0.5 | 0.6 |
| CH3OH | 1J(CH) | 134.2 | 133.6 | 125.5 | −0.1 | −0.3 | −0.2 | 0.4 | 0.3 | 0.3 | 0.6 | 0.6 | 0.6 |
| CH3NH2 | 1J(NH) | −60.0 | −62.1 | −58.7 | −0.2 | −0.1 | −0.1 | −2.9 | −2.7 | −2.6 | −0.2 | −0.2 | −0.2 |
| CH3OH | 1J(OH) | −55.9 | −66.9 | −64.2 | −0.6 | −0.3 | −0.5 | −12.0 | −11.2 | −11.0 | −0.2 | −0.2 | −0.3 |
| CH3CH3 | 1J(CC) | 31.3 | 37.1 | 32.7 | 1.1 | 1.0 | 1.0 | 0.0 | 0.1 | 0.2 | 0.1 | 0.1 | 0.1 |
| CH3NH2 | 1J(CN) | −1.2 | −5.2 | −3.9 | −0.8 | −0.7 | −0.7 | −0.3 | −0.5 | −0.5 | −0.1 | −0.1 | −0.1 |
| CH3OH | 1J(CO) | 23.5 | 14.7 | 16.1 | −1.9 | −1.7 | −1.7 | −1.7 | −1.9 | −2.0 | −0.1 | −0.1 | −0.1 |
3.2 Geminal coupling constants
| DFT | RASSCF | CCSD | exp. | ||
| CH3CH3 | 2J(CH) | −3.0 | −5.5 | −4.4 | −4.655 – −4.661 |
| CH3NH2 | 2J(CH) | −1.9 | −4.4 | −3.3 | – |
| CH3OH | 2J(CH) | −2.4 | −4.2 | −3.4 | – |
| CH3CH3 | 2J(HH) | −11.3 | −14.4 | −12.1 | – |
| CH3NH2 | 2J(HH)c | −10.1 | −13.3 | −11.1 | – |
| CH3NH2 | 2J(HH)’d | −7.6 | −10.8 | −9.3 | – |
| CH3OH | 2J(HH) | −9.2 | −12.4 | −10.2 | −10.8 |
| CH3NH2 | 2J(NH) | −3.0 | −0.7 | −0.9 | −1.0 (0.1) |
| CH3OH | 2J(OH) | −6.2 | −5.0 | −4.9 | −7.5 |
| Fermi contact | Spin-dipole | Paramagnetic SO | Diamagnetic SO | ||||||||||
| DFT | RAS | CCSD | DFT | RAS | CCSD | DFT | RAS | CCSD | DFT | RAS | CCSD | ||
| CH3CH3 | 2J(CH) | −3.1 | −5.6 | −4.5 | 0.1 | 0.1 | 0.1 | 0.4 | 0.4 | 0.4 | −0.3 | −0.3 | −0.3 |
| CH3NH2 | 2J(CH) | −2.1 | −4.6 | −3.5 | 0.1 | 0.1 | 0.1 | 0.7 | 0.7 | 0.7 | −0.6 | −0.6 | −0.6 |
| CH3OH | 2J(CH) | −2.6 | −4.5 | −3.6 | 0.0 | 0.1 | 0.0 | 0.9 | 0.9 | 0.9 | −0.7 | −0.7 | −0.7 |
| CH3CH3 | 2J(HH) | −11.9 | −15.0 | −12.6 | 0.4 | 0.4 | 0.4 | 3.0 | 3.0 | 3.0 | −2.9 | −2.9 | −2.9 |
| CH3NH2 | 2J(HH) | −10.6 | −13.8 | −11.5 | 0.4 | 0.5 | 0.4 | 2.9 | 2.8 | 2.8 | −2.8 | −2.8 | −2.8 |
| CH3NH2 | 2J(HH)’ | −9.1 | −12.2 | −10.6 | 0.6 | 0.7 | 0.6 | 5.6 | 5.4 | 5.4 | −4.8 | −4.8 | −4.8 |
| CH3OH | 2J(HH) | −9.7 | −12.9 | −10.6 | 0.5 | 0.5 | 0.5 | 2.9 | 2.8 | 2.8 | −2.9 | −2.9 | −2.8 |
| CH3NH2 | 2J(NH) | −2.8 | −0.6 | −0.8 | 0.0 | 0.0 | 0.0 | −0.3 | −0.3 | −0.3 | 0.1 | 0.2 | 0.2 |
| CH3OH | 2J(OH) | −5.6 | −4.5 | −4.3 | 0.1 | 0.2 | 0.1 | −1.0 | −0.9 | −0.9 | 0.2 | 0.2 | 0.2 |
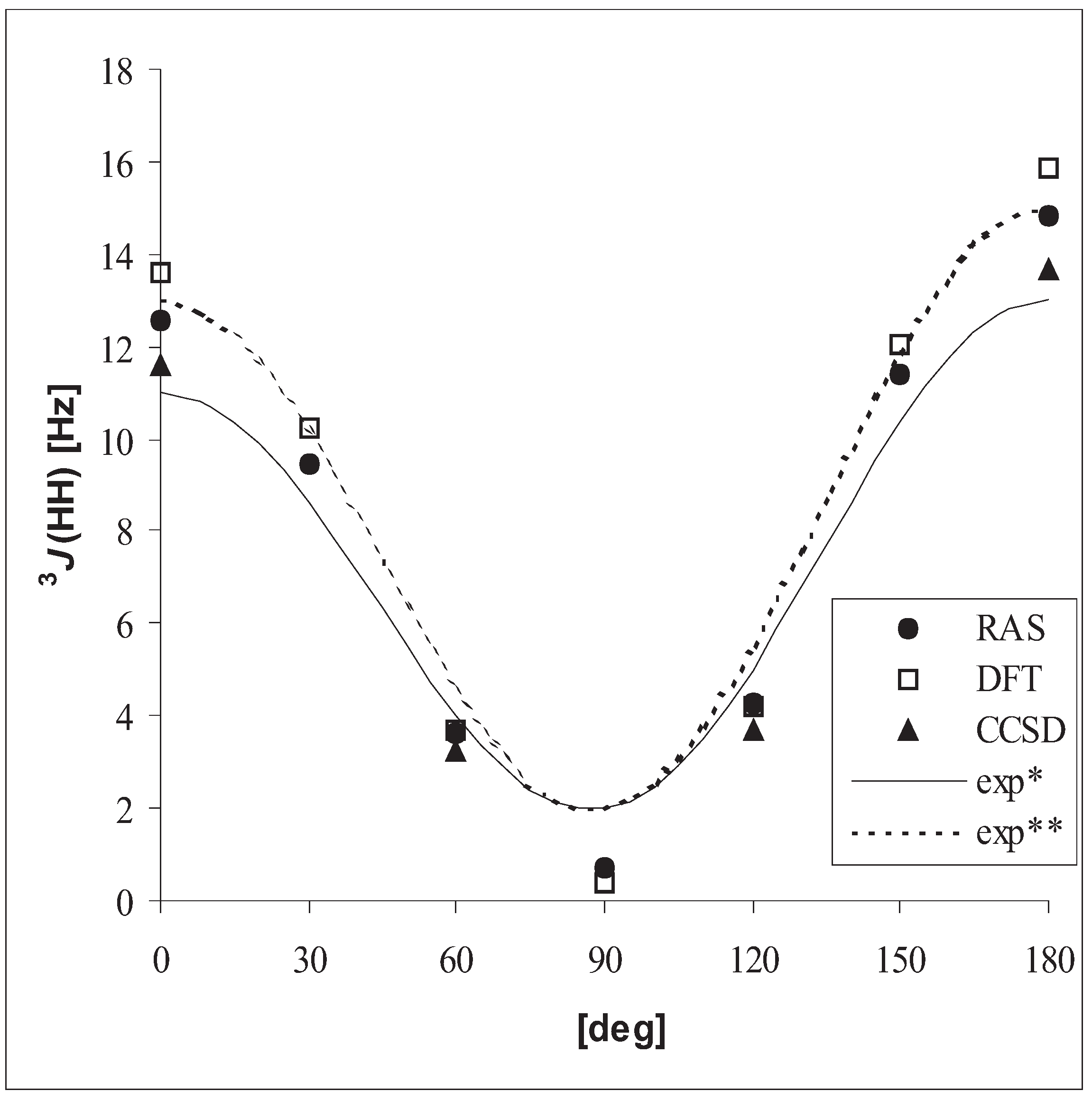
3.3 Vicinal coupling constants
| DFT | RASSCF | CCSD | exp. | ||
| CH3CH3 | 3J(HH) | 7.8 | 7.3 | 6.7 | 7.992 – 8.005 |
| CH3CH3 | 3J(HH) | 6.9 | 6.3 | 5.8 | 7.1 (0.1) |
| CH3OH | 3J(HH) | 5.9 | 5.1 | 4.8 | 5.0 |
| Fermi contact | Spin-dipole | Paramagnetic SO | Diamagnetic SO | ||||||||||
| DFT | RAS | CCSD | DFT | RAS | CCSD | DFT | RAS | CCSD | DFT | RAS | CCSD | ||
| CH3CH3 | 3J(HH) | 7.8 | 7.3 | 6.7 | 0.1 | 0.1 | 0.1 | 1.6 | 1.6 | 1.5 | −1.6 | −1.6 | −1.6 |
| CH3NH2 | 3J(HH) | 6.9 | 6.4 | 5.9 | 0.0 | 0.1 | 0.1 | 2.1 | 2.0 | 2.0 | −2.1 | −2.1 | −2.1 |
| CH3OH | 3J(HH) | 5.9 | 5.1 | 4.9 | 0.1 | 0.1 | 0.1 | 2.5 | 2.4 | 2.4 | −2.5 | −2.5 | −2.5 |
4 Summary and conclusions

Acknowledgments
References
- Karplus, M. Contact Electron-Spin Coupling of Nuclear Magnetic Moments. J. Chem. Phys. 1959, 30, 11–15. [Google Scholar] [CrossRef]
- Karplus, M. Vicinal Proton Coupling in NMR. J. Am. Chem. Soc. 1963, 85, 2870–2871. [Google Scholar] [CrossRef]
- Minch, M. J. Orientational Dependence of Vicinal Proton-Proton NMR Coupling Constants: The Karplus Relationship. Conc. Magn. Reson. 1994, 6, 41–56. [Google Scholar] [CrossRef]
- Juranic, N.; Ilich, P. K.; Macura, S. Hydrogen Bonding Networks in Proteins As Revealed by the Amide 1JNC′ Coupling Constant. J. Am. Chem. Soc. 1995, 117, 405–410. [Google Scholar] [CrossRef]
- Helgaker, T.; Jaszuński, M.; Ruud, K. Ab initio methods for the calculation of NMR shielding and indirect spin-spin coupling constants. Chem. Rev. 1999, 99, 293–352. [Google Scholar] [CrossRef] [PubMed]
- de Dios, A. C. Ab initio calculations of the NMR chemical shift. Prog. NMR. Spectrosc. 1996, 29, 229–278. [Google Scholar] [CrossRef]
- Fukui, H. Theory and calculation of nuclear shielding constants. Prog. NMR. Spectrosc. 1997, 31, 317–342. [Google Scholar] [CrossRef]
- Pecul, M.; Leszczynski, J.; Sadlej, J. The shielding constants and scalar couplings in N-H…O=C and N- H…N=C hydrogen bonded systems: an ab initio MO study. J. Phys. Chem. A 2000, 104, 8105–8113. [Google Scholar]
- Scheurer, C.; Brüschweiler, R. Quantum-Chemical Characterization of Nuclear Spin-Spin Couplings Across Hydrogen Bonds. J. Am. Chem. Soc. 1999, 121, 8661–8662. [Google Scholar] [CrossRef]
- Peralta, J. E.; Barone, V.; Contreras, R. H. Through-Bond and Through-Space JFF Spin-Spin Couplings in Perifluoronaphtalenes: Accurate DFT Evaluation of the Four Contribution. J. Am. Chem. Soc. 2001, 123, 9162–9163. [Google Scholar] [CrossRef] [PubMed]
- Malkin, V. G.; Malkina, O. L.; Salahub, D. R. Calculation of spin-spin coupling constants using density functional theory. Chem. Phys. Lett. 1994, 221, 91–99. [Google Scholar] [CrossRef]
- Malkina, O. L.; Salahub, D. R.; Malkin, V. G. Nuclear magnetic resonance spin-spin coupling constants from density functional theory: Problems and results. J. Chem. Phys. 1996, 105, 8793–8800. [Google Scholar] [CrossRef]
- Sychrovský, V.; Grӓfenstein, J.; Cremer, D. Nuclear magnetic resonance spin–spin coupling constants from coupled perturbed density functional theory. J. Chem. Phys. 2000, 113, 3530–3547. [Google Scholar] [CrossRef]
- Helgaker, T.; Watson, M.; Handy, N. C. Analytical calculation of nuclear magnetic resonance spin-spin coupling constants at the generalized gradient approximation and hybrid levels of density functional theory. J. Chem. Phys. 2000, 113, 9402–9409. [Google Scholar] [CrossRef]
- Dickinson, R. M.; Ziegler, T. NMR Spin-Spin Coupling Constants from Density Func-tional Theory with Slater-Type Basis Fuunctions. J. Phys. Chem. 1996, 100, 5286–5290. [Google Scholar] [CrossRef]
- Lantto, P.; Vaara, J.; Helgaker, T. Spin–spin coupling tensors by density-functional linear response theory. J. Chem. Phys. 2002, 117, 5998–6009. [Google Scholar] [CrossRef]
- Becke, A. D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Stephens, P. J.; Devlin, F. J.; Chabalowski, C. F.; Frisch, M. J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Helgaker, T.; Jensen, H. J. A.; Jørgensen, P.; Olsen, J.; Ruud, K.; ˚Agren, H.; Auer, A. A.; Bak, K. L.; Bakken, V.; Christiansen, O.; Coriani, S.; Dahle, P.; Dalskov, E. K.; Enevoldsen, T.; Fernandez, B.; H¨attig, C.; Hald, K.; Halkier, A.; Heiberg, H.; Hettema, H.; Jonsson, D.; Kirpekar, S.; Kobayashi, R.; Koch, H.; Mikkelsen, K. V.; Norman, P.; Packer, M. J.; Pedersen, T. B.; Ruden, T. A.; Sanchez, A.; Saue, T.; Sauer, S. P. A.; Schimmelpfenning, B.; Sylvester-Hvid, K. O.; Taylor, P. R.; Vahtras, O. dalton, an ab initio electronic structure program, Release 1.2 (2001). See http://www.kjemi.uio.no/software/dalton/dalton.html.
- Vahtras, O.; ˚Agren, H.; Jørgensen, P.; Jensen, H. J. A.; Padkjær, S. B.; Helgaker, T. Indirect nuclear spin-spin coupling constants from multiconfigurational linear response theory. J. Chem. Phys. 1992, 96, 6120–6125. [Google Scholar] [CrossRef]
- Pecul, M.; Jaszuński, M.; Sadlej, J. The geometry dependence of the spin-spin coupling constants in ethane: a theoretical study. Chem. Phys. Lett. 1999, 305, 139–145. [Google Scholar] [CrossRef]
- Pecul, M.; Sadlej, J. The nuclear spin-spin coupling constants in methanol and methy-lamine: geometry and solvent effects. Chem. Phys. 2000, 255, 137–148. [Google Scholar] [CrossRef]
- Auer, A. A.; Gauss, J. Triple excitation effects in coupled-cluster calculations of indirect spin-spin coupling constants. J. Chem. Phys. 2001, 115, 1619–1622. [Google Scholar] [CrossRef]
- Stanton, J. F.; Gauss, J.; Watts, J. D.; Lauderdale, W. J.; Bartlett, R. J. The Aces II Program System. Int. J. Quantum Chem.:Quantum Chem. Symp. 1992, 26, 879–894. [Google Scholar] [CrossRef]
- Szalay, P. G.; Gauss, J.; Stanton, J. Analytic UHF-CCSD(T) second derivatives. Theor. Chem. Acc. 1998, 100, 5–11. [Google Scholar] [CrossRef]
- Hirota, E.; Endo, Y.; Saito, S. Microwave Spectra of Deuterated Ethanes: Internal Rotation Potential Function and rz Structure. J. Mol. Spectrosc. 1981, 89, 285–295. [Google Scholar] [CrossRef]
- Takagi, K.; Kojima, T. Microwave spectrum of methylamine. J. Phys. Soc. Japan. 1971, 30, 1145–1157. [Google Scholar] [CrossRef]
- Gerry, M. C. L.; Lees, R. M.; Winnewisser, G. The torsion-rotation microwave spectrum of 12CH318OH and the structure of methanol. J. Mol. Spectrosc. 1976, 61, 231–242. [Google Scholar] [CrossRef]
- Schindler, M.; Kutzelnigg, W. Theory of magnetic susceptibilities and NMR chemical shifts in terms of localized quantities. II.Application to some simple molecules. J. Chem. Phys. 1982, 76, 1919–1933. [Google Scholar] [CrossRef]
- Kaski, J.; Lantto, P.; Vaara, J.; Jokisaari, J. Experimental and Theoretical ab initio Study of the 13C-13C Spin-Spin Coupling and 1H and 13C Shielding Tensors in Ethane, Ethene and Ethyne. J. Am. Chem. Soc. 1998, 120, 3993–4005. [Google Scholar] [CrossRef]
- Lazzeretti, P. Calculation of nuclear spin-spin coupling constants in methanol molecule. J. Chem. Phys. 1979, 71, 2614–2521. [Google Scholar] [CrossRef]
- Paolillo, L.; Becker, E. D. The Relative Signs of the Spin-Spin Coupling Constants in CH3NH2. J. Magn. Reson. 1970, 3, 200–203. [Google Scholar]
- Helgaker, T.; Jaszuński, M.; Ruud, K.; Górska, A. Basis set dependence of nuclear spin-spin coupling constants. Theor. Chim. Acc. 1998, 99, 175–182. [Google Scholar] [CrossRef]
- Kirpekar, S.; Enevoldsen, T.; Oddershede, J.; Raynes, W. T. Vibrational and thermal averaging of the indirect nuclear spin-spin coupling constants of CH4, SiH4, GeH4, and SnH4. Mol. Phys. 1997, 91, 897–907. [Google Scholar] [CrossRef]
- Ruden, T. A.; Lutnæs, O. B.; Helgaker, T.; Ruud, K. Vibrational corrections to indirect nuclear spin-spin coupling constants calculated by density-functional theory. J. Chem. Phys. submitted.
- Pecul, M.; Dodziuk, H.; Jaszuński, M.; Lukin, O.; Leszczynski, J. Ab initio calculations of the NMR spectra of [1,1,]propellane and bicyclo[1,1,1]pentane. Phys. Chem. Chem. Phys. 2001, 3, 1986–1991. [Google Scholar] [CrossRef]
© 2003 by MDPI, Basel, Switzerland. Reproduction for noncommercial purposes permitted.
Share and Cite
Pecul, M.; Helgaker, T. The Spin–Spin Coupling Constants in Ethane, Methanol and Methylamine: A Comparison of DFT, MCSCF and CCSD Results. Int. J. Mol. Sci. 2003, 4, 143-157. https://0-doi-org.brum.beds.ac.uk/10.3390/i4030143
Pecul M, Helgaker T. The Spin–Spin Coupling Constants in Ethane, Methanol and Methylamine: A Comparison of DFT, MCSCF and CCSD Results. International Journal of Molecular Sciences. 2003; 4(3):143-157. https://0-doi-org.brum.beds.ac.uk/10.3390/i4030143
Chicago/Turabian StylePecul, Magdalena, and Trygve Helgaker. 2003. "The Spin–Spin Coupling Constants in Ethane, Methanol and Methylamine: A Comparison of DFT, MCSCF and CCSD Results" International Journal of Molecular Sciences 4, no. 3: 143-157. https://0-doi-org.brum.beds.ac.uk/10.3390/i4030143