Introduction
The study of electron-capture processes by atomic and molecular ions from atomic and molecular targets has recently received considerable attention. These processes are of interest as they are most likely to have impact on field such as low- and high-temperature plasma, astrophysics, atmospheric science and even material science. At low collision energies, there are also fundamental physics issues that have yet to be resolved. At such low energies, the collision process possesses strong molecular features, which yields stringent test for theoretical calculations.
Systematic studies of electron-capture processes in which low- and high-energy primary ion, in collision with neutral molecular or atomic gas, captures a single electron or double electrons have been the subject of both experimental exploration and theoretical discussion for a number of years. Experimentally, the cross sections for electron-capture processes by low-energy ions from a neutral gas and their variation with the ion energy have been reported [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20,
21,
22,
23,
24,
25,
26,
27,
28,
29,
30]. However, the experimental measurements are confined mainly to inert and hydrogen gases [
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16].
Concerning theoretical investigation, it has been found that several models [
17,
18,
19] explain those electron-capture processes by low-energy ions from certain atomic and molecular gases. Electron-capture cross sections involving heavy targets such as
N2 are intractable in any model calculation. The reasons for this are obvious; the complex multi-electron systems cannot be described classically to a good approximation; and the quantum-mechanical study of these multi-electron systems in the time-dependent field is very complicated. While few such treatments presently exist in the literature [
7], the increasing availability of the experimental measurements especially at low collision energies may stimulate work in this direction.
It thus becomes apparent that more measurements of the electron-capture cross sections involving heavy-target and low collision energies are needed. The work presented here focuses on the following exothermic electron-capture reaction:
where ∆E represents the energy gain. Depending upon the electronic state of the incident ions, different sets of ∆E values could be obtained. For this reaction ∆E is positive only for
incident ions, which are in an electronically-excited state. For
incident ions, which are in ground-state the reaction is an endothermic one with ∆E of –3.51 eV. Thus, for
with
N2 collisions, capture is predominately into the electronically-excited states of
. The ground-state of
plays no role in electron-capture into the ground-state of
N2. The reaction of
incident ions in the ground- state with
N2 is:
Whereas, the reactions of
incident ions in a metastable, electronically-excited states with
N2 are:
Similar set of ΔE values can be computed for higher-excited states of
.
We have utilized the notation of Kamber
et. al. [
20] to denote these channels in the following fashion: the Roman numerical I and II represent, respectively, the ground and first electronically-excited states of the projectile species, whereas the Greek letters α, β,… represent the ground and subsequent electronically-excited states of the neutral products of
O2. Thus, for example, Iα denotes capture by X
2 Π
g ground-state of
into X
3Σg ground-state of
O2, whereas IIα represents capture by the first exited-state of
into the ground-sate of
O2. The ionization energies to
and
are listed in Ref. 21.
Experiment
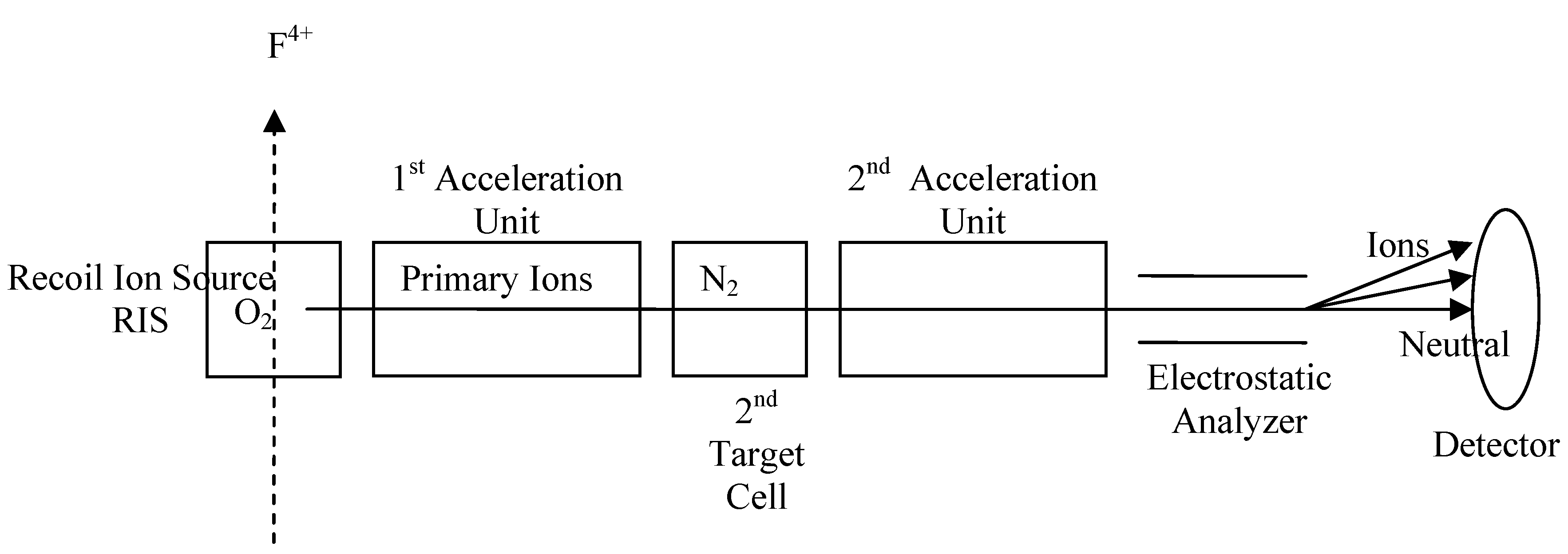
The experiment is carried out in the recoil ion source apparatus, which in many respects is similar to the apparatus used in Ref’s. 22-24. A schematic diagram of this apparatus is shown in
Fig. 1. A 10-pA, 1.5-ns pulsed F
4+ beam, of energy 1 MeV/amu and a diameter of approximately 2 mm with a divergence of 5 mrad from the Kansas State University Tandem Van de Graaff accelerator is directed into the recoil ion source (RIS) containing
O2 the molecular gas. The collisions that take place in the RIS between the fast F
4+ pulsed beam and the gas molecules generate recoil (primary) ions that are extracted by the voltage gradient across the RIS electrodes. Upon exiting the RIS, these ions travel through the first acceleration unit, a seven-plate apparatus, which only the fifth plate is not grounded. This plate (Einzel lens) focuses and drifts the primary ions toward the secondary pressurized gas-target cell, which is 31.8 cm away from the detector, containing the
N2 molecular gases. Collisions between low-energy primary ions and the gas molecule occur resulting in further loss or gain of electron (s) by either or both of the primary ions, and the target molecules. After exiting the gas target cell, the ions move through a second acceleration unit, which is identical to the first acceleration unit. The focused low-energy ions move to the detector through an electrostatic analyzer.
The gas pressures in the RIS (1.77 mTorr) and the secondary gas-target cell (7.0 mTorr) are monitored by MKS type 90 capacitance manometers and controlled by servo-assisted gas-handling system, which regulates a Granville-Philips variable leak valves. The background pressure of the beam line is maintained at about 5 × 10−7 Torr.
Figure 1.
A schematic diagram shows the experimental arrangement.
Figure 1.
A schematic diagram shows the experimental arrangement.
The time-of-flight (TOF) and the final charge state of the primary ion are the basis of our measurements, thus a fast coincidence technique is used. By applying an appropriate potential at the analyzer selected charge state ions are allowed to reach the detector. The use of this electrostatic analyzer in conjunction with TOF techniques allow the identification of various events associated with the charged molecular ions. The primary ion created in the RIS are identified by its TOF, that is the time it takes an ion to travel from its creation to its detection by the detector. This TOF is proportional to the , where m is the mass of the ion; d is its flight-path-length (~ 68 cm); q is its charge; and Vo is the voltage gradient across the RIS electrodes.
A separation between these primary ions and the ions created in the secondary gas-target cell can also be achieved by the help of the analyzer voltage in conjunction with the TOF, while the neutral products pass straight through the analyzer without deflection into the detector. A second collision charge change of the primary ions within the secondary gas-target cell would have to occur, thus the pressure of the secondary gas-target cell is kept sufficiently low to minimize this process.
The absolute total cross section for single-electron-capture is then evaluated using the following mathematical formula [
1,
3,
4,
22,
23,
24]:
where
Nneut is the number of the neutral products per second detected;
is the total number of primary ions per second (
) entering the secondary gas-target cell; n is the number of the target molecules per unit volume (target density ~ 8.89 × 10
13 molecules/cm
3); and L is the length of the secondary target cell (L = 2 cm).
Nneut is determined by applying a transverse field on the analyzer to deflect the ions away after they pass through the second acceleration unit, allowing only the neutral products to impact the detector. The primary ions can be identified by their TOF’s by removing the transverse field and by applying an appropriate voltage on the analyzer. The resulting number of primary ions and their neutral products is equal to
(i.e. it is the number of ions per second entering the second gas-target cell). The ions and the neutral products are detected with the same efficiency (ε = 40% [
1,
22,
23,
24]).
In general, for these types of experiments, the absolute total cross section for electron capture may be determined in two ways; first, those experiments in which the cross sections are determined by measuring the fast neutral products, and utilized by us, Lindsay
et al. [
3], and Moran
et al. [
4]; and second, those experiments in which the slow ion products are measured, and implemented by, Flesch
et al. [
25], and Li
et al. [
26]. In fact, these two types of measurements lead to the same result.
Result and Conclusion
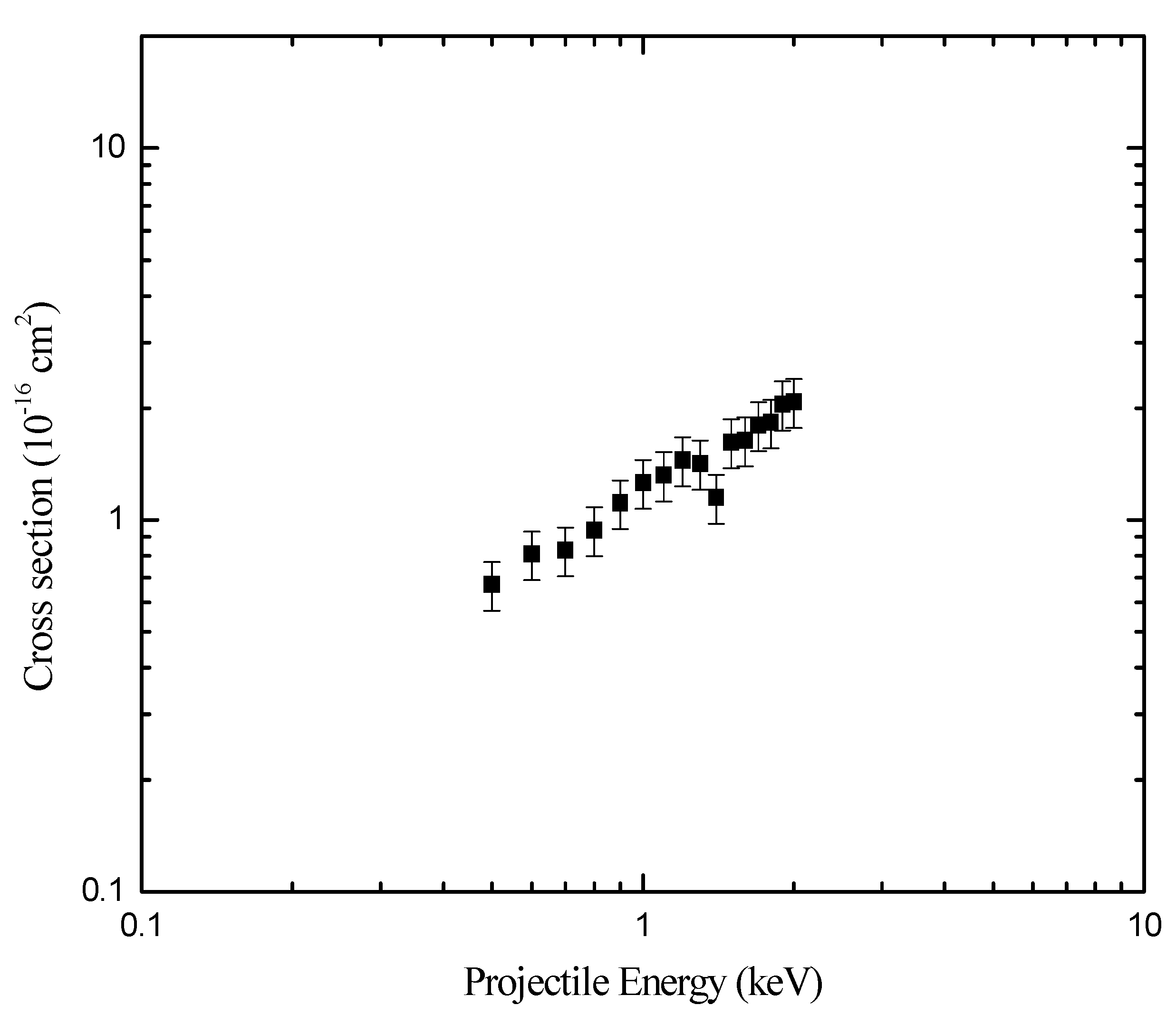
The dependence of the single-electron-capture cross sections on primary ions kinetic energies (0.50 to 2.00 keV) are measured for
+
N2 system at RIS pressure of ~ 1.77 mTorr, and a secondary gas-target cell pressure of ~ 7.0 mTorr. These cross sections are reported in
Table 1, and shown in
Fig. 2. Overall uncertainties in the measurements are in the order of 15%, which arise from the determination of the effective length of the target cell 7%; the counting statistics 3%; and the summing up the yield in the peak 5%.
The energy dependence of the total cross sections for single-electron-capture are measured and found to slowly increase with increasing incident energy, except at 1.4 keV. The trend of increasing cross sections as a function of incident energy is also shown by the previous measurements of Lindsay
et al. [
3] and Moran
et al. [
4] for
+
N2 system. Several measurements of total cross sections for electron-capture from
O2 by slow
ions [
2] and from
N2 by slow
[
1,
2] and
O+ [
3,
4] ions presently exist in the literature. The level of agreement of all previous measurements with theoretical predictions where available is between good to fair. In the measurements reported here, we measured the total cross sections for electron-capture from
N2 by slow
ions, such measurements are not found in the literature. The increasing availability of data on this system may stimulate work in this direction.
Table 1.
Absolute total single-electron-capture cross sections, σ (Å2), for + N2, collisions are listed. Overall uncertainties in each value are15%.
Table 1.
Absolute total single-electron-capture cross sections, σ (Å2), for + N2, collisions are listed. Overall uncertainties in each value are15%.
| E(keV) | σ + N2 |
|---|
| 0.5 | 0.67 |
| 0.6 | 0.81 |
| 0.7 | 0.83 |
| 0.8 | 0.94 |
| 0.9 | 1.11 |
| 1.0 | 1.26 |
| 1.1 | 1.32 |
| 1.2 | 1.45 |
| 1.3 | 1.42 |
| 1.4 | 1.15 |
| 1.5 | 1.62 |
| 1.6 | 1. 64 |
| 1.7 | 1.80 |
| 1.8 | 1.83 |
| 1.9 | 2.05 |
| 2.0 | 2.08 |
Figure 2.
Dependence of the absolute total single-electron-capture cross section of + N2 the projectile energy.
Figure 2.
Dependence of the absolute total single-electron-capture cross section of + N2 the projectile energy.