6. Calculation Results and Discussion
In the present report 28 local anaesthetics analogues of procaine (
cf.
Table 1) have been studied. The analysis includes such chemical compounds that fit the following general scheme: lipophilic portion–intermediate chain–hydrophilic portion, since among the species used in practice of local anaesthesia, these are the most numerous and have the widest range of uses. The lipophilic portion normally consists of at least one phenyl radical; the hydrophilic portion is most often a secondary or tertiary amine; the intermediate chain commonly has an ester or amide linkage. The matrix of Pearson correlation coefficients between each pair of vector properties <
i1,
i2,
i3,
i4,
i5> of the 28 anaesthetics has been calculated. The intercorrelations are illustrated in the partial correlation diagram, which contains 133 high partial correlations (
r ≥ 0.75,
cf.
Figure 1,
red lines), 76 medium partial correlations (0.50 ≤
r < 0.75,
orange lines), and 22 low partial correlations (0.25 ≤
r < 0.50,
yellow lines). Pairs of anaesthetics with high partial correlations have a similar vector property (
Table 1). However, the results (
Figure 1) should be taken with care, because four compounds show the constant <11111> vector (Entries 4, 6, 20 and 23 in
Table 1), for which the null standard deviation causes high partial correlations (
r = 1) with any local anaesthetic, which is an artifact.
Figure 1.
Partial correlation diagram: High (red), medium (orange) and low (yellow) correlations.
Figure 1.
Partial correlation diagram: High (red), medium (orange) and low (yellow) correlations.
Using the grouping rule in the drug-design case with equal weights
ak = 0.5, for 0.94 ≤
b1 ≤ 0.96 the following set of classes are obtained [
17]:
![Ijms 07 00012 i027]()
= (1,21,22)(2,5)(3,13,15,16,19,24,28)(4,6,20,23)(7,8)(9,26)(10)(11,18,25)(12)(14,17)(27)
The 11 classes are obtained with the associated entropy
![Ijms 07 00012 i028]()
= 58.86. The dendrogram (binary tree) [
23,
24] matching to <
i1,
i2,
i3,
i4,
i5> and
![Ijms 07 00012 i027]()
is illustrated [
25] in
Figure 2. It provides a binary taxonomy of
Table 1, which separates the same 11 classes. In particular, the ester (benzocaine, 2-chloroprocaine, procaine, tetracaine) and amide local anaesthetics (bupivacaine, dibucaine, etidocaine, lidocaine, mepivacaine, prilocaine, S-ropivacaine) are always grouped in different classes. The agents of low potency and short duration (procaine, 2-chloroprocaine) are separated from the agents of high potency and long duration (bupivacaine, etidocaine, S-ropivacaine), while the agents of moderate potency and duration (mepivacaine, prilocaine) are classified together with the latter. Those anaesthetics belonging to the same class appear higly correlated in the partial correlation diagram (
Figure 1), in agreement with previous results obtained for the first 27 entries in
Table 1 [
17].
Figure 2.
Dendrogram for the local anaesthetics analogues of procaine at level b1.
Figure 2.
Dendrogram for the local anaesthetics analogues of procaine at level b1.
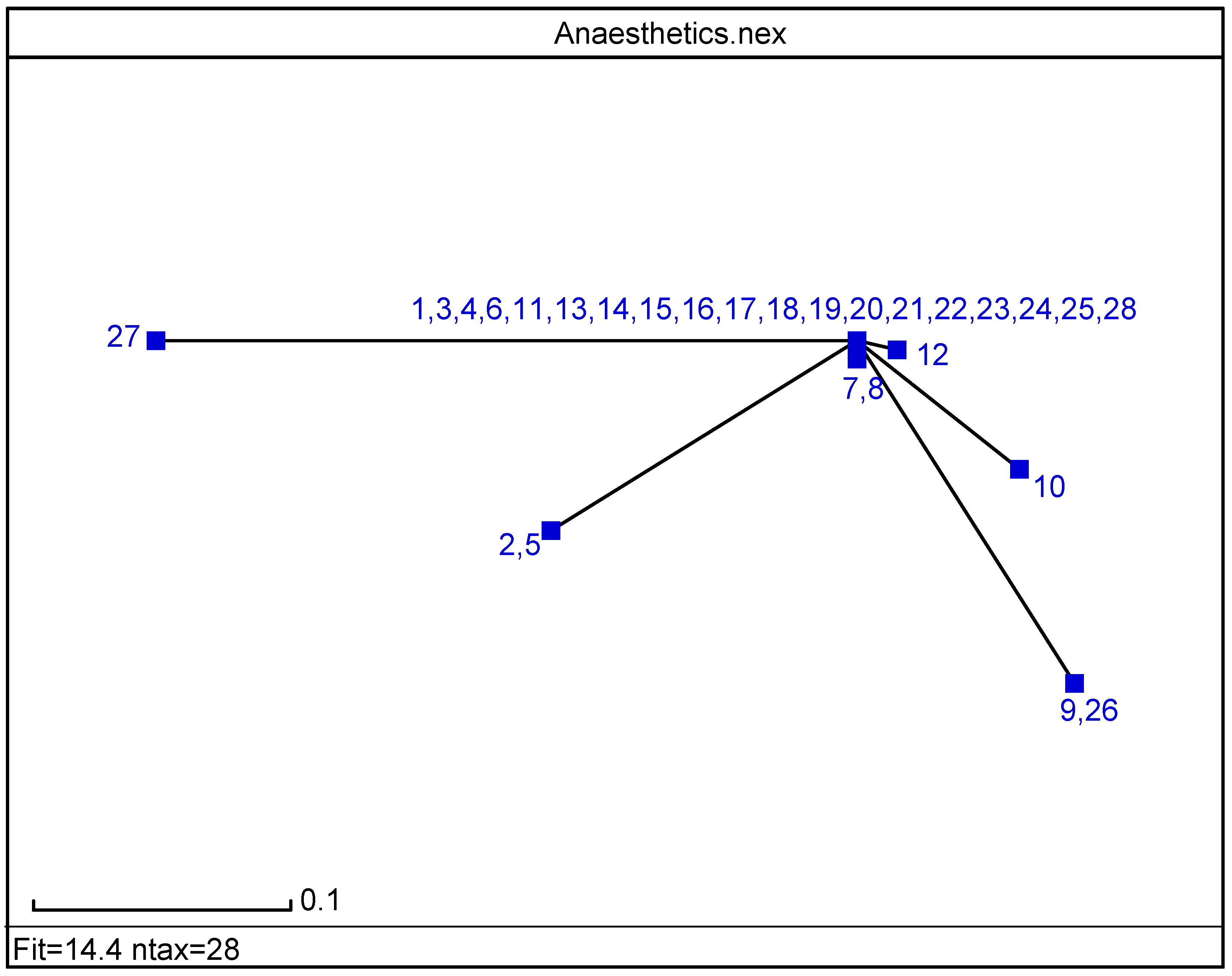
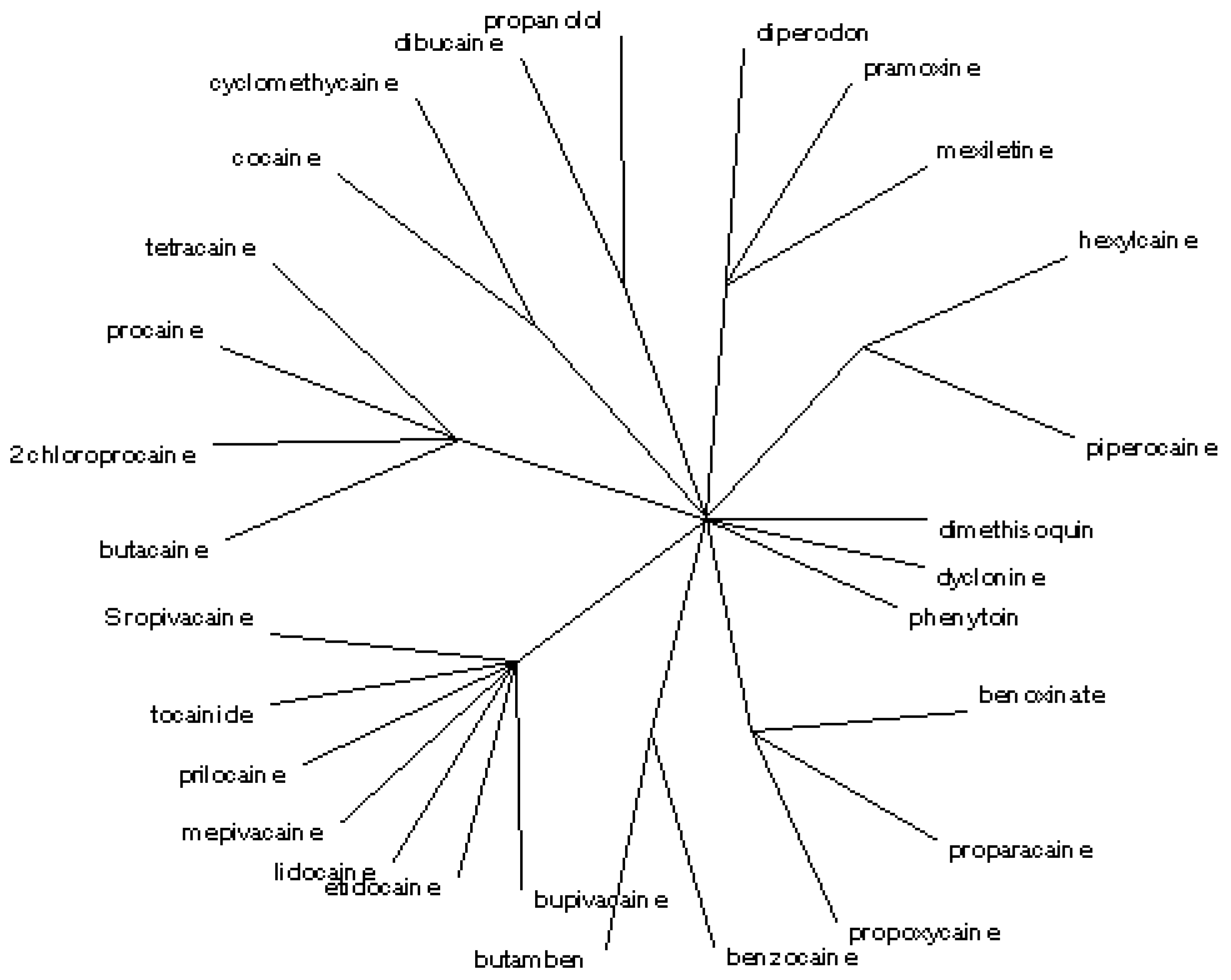
The radial tree for the local anaesthetics relating to <
i1,
i2,
i3,
i4,
i5> and
Cb1 (
cf.
Figure 3) separates the same 11 classes, in agreement with the partial correlation diagram, dendrogram (
Figure 1 and
Figure 2) and previous results obtained for the first 27 entries in
Table 1 [
17].
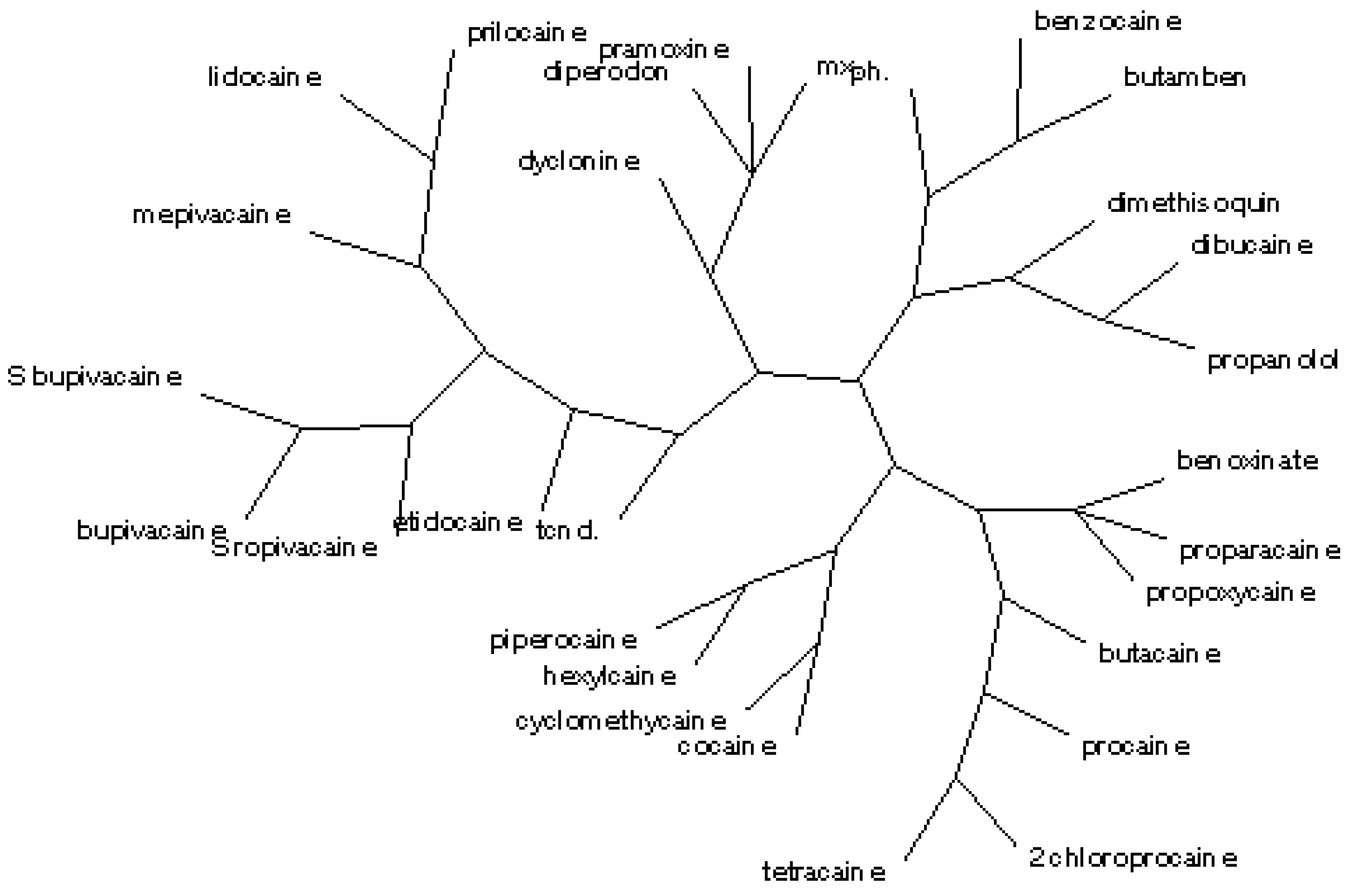
Figure 3.
Radial tree for the local anaesthetics analogues of proacine at level b1.
Figure 3.
Radial tree for the local anaesthetics analogues of proacine at level b1.
At level
b2 with 0.85 ≤
b2 ≤ 0.87 the set of classes is [
17]
![Ijms 07 00012 i029]()
= (1,4,6,7,8,14,17,20,21,22,23)(2,5)(3,11,12,13,15,16,18,19,24,25,28)(9,10,26)(27)
Five classes result in this case; the entropy is
![Ijms 07 00012 i030]()
= 12.20. The radial tree matching to <
i1,
i2,
i3,
i4,
i5> and
![Ijms 07 00012 i029]()
(cf.
Figure 4) separates the same five classes, in agreement with the partial correlation diagram, dendrogram, binary tree (
Figure 1,
Figure 2 and
Figure 3) and previous results obtained for the first 27 entries in
Table 1 [
17]. A high degree of similarity is found for Entries 9 and 26 (
i.e. dibucaine and propanolol), as well as Entries 2 and 5 (
i.e. benzocaine and butamben). Again, the ester and amide local anaesthetics are grouped in different classes; the agents of low potency and short duration are separated from the agents of high–medium potency and long–medium duration. The lower level
b2 classification process shows lower entropy and, therefore, may be more parsimonious. The classification model divides the point process into two components,
viz. signal, and noise; the lower-level
b2 may have greater signal-to-noise ratio than the higher-level
b1 classification process. Naturally, Entries 4, 6, 20 and 23 (
i.e. butacaine, 2-chloroprocaine, procaine and tetracaine) belong to the same class at any grouping level
b, except at the highest level above which each class contains only one species. A detailed classification at level
b1 into 11 classes, and a less detailed classification at a lower level
b2 into five classes can be selected, taking into account the amount of entropy variation.
Figure 4.
Radial tree for the local anaesthetics analogues of procaine at level b2.
Figure 4.
Radial tree for the local anaesthetics analogues of procaine at level b2.
A comparative analysis of the set containing from one to 11 classes is summarized in
Table 2, in agreement with previous results obtained for the first 27 entries in
Table 1 [
17].
Table 2.
Classification level, number of classes and entropy for the local anaesthetics.
Table 2.
Classification level, number of classes and entropy for the local anaesthetics.
| Classification level b | Number of classes | Entropy h |
|---|
| 0.96 | 11 | 59.65 |
| 0.93 | 8 | 31.31 |
| 0.87 | 5 | 12.00 |
| 0.78 | 4 | 7.23 |
| 0.75 | 3 | 3.95 |
| 0.56 | 2 | 1.66 |
| 0.25 | 1 | 0.14 |
From the set containing from one to 11 classes (
Table 2), the radial tree matching to <
i1,
i2,
i3,
i4,
i5> and
![Ijms 07 00012 i031]()
(
cf.
Figure 5) separates the same five and 11 classes, in agreement with the partial correlation diagram, dendrogram, binary trees (
Figure 1,
Figure 2,
Figure 3 and
Figure 4) and previous results obtained for the first 27 entries in
Table 1 [
17]. Again, the ester and amide local anaesthetics are grouped in different classes; the agents of low potency and short duration are separated from the agents of high–medium potency and long–medium duration.
Figure 5.
Radial tree for the local anaesthetics analogues of procaine from 1 to 11 classes.
Figure 5.
Radial tree for the local anaesthetics analogues of procaine from 1 to 11 classes.
The resulting partition into classes compares well with other from Covino considered as
good [
8]. He compared three ester,
viz. 2-chloroprocaine, procaine, and tetracaine, as well as five amide local anaesthetics,
viz. bupivacaine, etidocaine, lidocaine, mepivacaine, and prilocaine, based on chemical configuration (aromatic lipophilic group, intermediate chain and amine hydrophilic group), four physicochemical properties (molecular weight, p
Ka, partition coefficient and protein binding), as well as three pharmacological properties (onset, relative potency and duration). The onset is determined primarily by p
Ka. The percentage of a local anaesthetic that is present in the neutral form, when injected to tissue of p
H 7.4, decreases with p
Ka, according to the equation of Henderson–Hasselbalch: p
H = p
Ka + log ([PR]/[PRH
+]). The potency is determined primarily by lipid solubility, which increases with partition coefficient. Both lipid solubility and partition coefficient are mainly due to the neutral forms. Different conformations have different partition coefficients, lipid solubilities and potencies. It would be of interest to study the effect of different intermediate chain lengths. In particular, the presence of a double bond in a chain would increase rigidity and enhance potency;
e.g., the conjugated enol group in 3-phenyl-2-propen-1-ol determines a greater membrane permeability, with respect to 3-phenyl-1-propanol [
26]. On the one hand, esters are hydrolyzed easily and are relatively unstable in solution; on the other, amides are much more stable. In the body, the amino esters are hydrozed in plasma by the enzyme cholinesterase, whereas the amino amides undergo enzymatic degradation in the liver.
The inclusion of this comparison [
8] in the radial tree of the present work (
cf.
Figure 6) is in agreement with the partial correlation diagram, dendrogram, binary trees (
Figure 1,
Figure 2,
Figure 3,
Figure 4 and
Figure 5) and previous results obtained for the first 27 entries in
Table 1 [
17]. The classification scheme from 1 to 11 levels is conserved after the addition of Entry 28 (S-ropivacaine) and local anaesthetic S-bupivacaine. In particular, Fawcett
et al. compared S-bupivacaine with racemic bupivacaine [
27]. S-ropivacaine is structurally close to bupivacaine; the main difference is that the former is a pure S-(–) enantiomer where the latter is a racemate. Again, the ester and amide local anaesthetics are grouped in different classes; the agents of low potency and short duration are separated from the agents of high–medium potency and long–medium duration. Moreover, the classification presents lower bias and greater precision, resulting in lower divergence with respect to the original distribution. Therefore, the approach is quite general. However, the inclusion of other local anaesthetics could change the detail,
i.e. subsequent classifications with more than 11 levels. A natural trend is to interchange similar anaesthetics in the composition of complex drugs,
e.g. the eutectic mixture of local anaesthetics (EMLA
®, lidocaine–prilocaine 2.5/2.5% w [
28]). However, mixtures of dissimilar anaesthetics are also used,
e.g., betacaine-LA (lidocaine–prilocaine–dibucaine) [
29] and S-caine (1:1 lidocaine–tetracaine eutectic mixture) [
30].
Figure 6.
Radial tree for anaesthetics including physicochemical and pharmacological properties.
Figure 6.
Radial tree for anaesthetics including physicochemical and pharmacological properties.
The predictions for topical anaesthetics and ice, both not included in the models, are included in
Table 3. The predictions have been compared with experimental results [
29,
30]. The relative potency is obtained from the mean pain scores after application of topical anaesthetics for 60 minutes [
29,
30]. ELA-max is superior to tetracaine and betacaine-LA at 60 minutes, while EMLA
® is superior to betacaine-LA at 60 minutes, which is in partial agreement with our prediction. The relative potency after removal is obtained from the mean pain scores 30 minutes after removal of the topical anaesthetics [
29,
30]. ELA-max and EMLA
® are superior to tetracaine and betacaine-LA 30 minutes after the 60-minute application period, which is in partial agreement with our prediction. Increased anaesthetic benefit is obtained 30 minutes after removal, which suggests that a reservoir of anaesthetic is located and stored in the upper skin layers during application, providing additional anaesthetic benefit after removal (
Table 3). Although EMLA
® is more potent than ice, ice has advantages in easy of use, fast action, and is less expensive than EMLA
® [
31].
Table 3.
Predictions for topical anaesthetics and ice both not included in the models.
Table 3.
Predictions for topical anaesthetics and ice both not included in the models.
| Anaesthetic | Ingredients | | Prediction | Experiment |
|---|
| | | Onset | Potency | Duration | Relative potencya | Rel. pot. afterb |
|---|
| Betacaine-LA | lidocaine:prilocaine:dibucaine | rapid | moderate | moderate | 1.0 | 1.0 |
| ELA-max | 4% lidocaine | rapid | moderate | moderate | 1.5 | 1.5 |
| ELA-max 5 | 5% lidocaine | rapid | moderate | moderate | – | – |
| EMLA cream | 2.5% lidocaine:2.5% prilocaine | rapid | moderate | moderate | 1.4 | 1.5 |
| Tetracaine gel | 4% tetracaine gel | slow | high | long | 1.2 | 1.1 |
| Amethocaine | 4% tetracaine | slow | high | long | – | – |
| Topicaine | 4% lidocaine | rapid | moderate | moderate | – | – |
| S-caine | 2.5% lidocaine:2.5% tetracaine | moderate | moderate-high | moderate-high | – | – |
| Icec | | moderate | low | low | <1.4 | <1.5 |
SplitsTree is a program for analyzing cluster analysis (CA) data [
32]. Based on the method of
split decomposition, it takes as input a
distance matrix or a set of CA data, and produces as output a graph that represents the relationships between the taxa. For ideal data this graph is a tree whereas less ideal data will give rise to a tree-like network, which can be interpreted as possible evidence for different and conflicting data. Furthermore, as split decomposition does not attempt to force data onto a tree, it can provide a good indication of how
tree-like given data are. The splits graph for the 28 local anaesthetics of
Table 1 (
cf.
Figure 7) reveals no conflicting relationship between the anaesthetics. In particular compounds 1, 3, 4, 6, 11, 13–25 and 28 appear superimposed. The splits graph is in general agreement with the partial correlation diagram, dendrogram and binary trees (
Figure 1,
Figure 2,
Figure 3,
Figure 4,
Figure 5 and
Figure 6). The main difference is the partial fusion of
![Ijms 07 00012 i029]()
classes (1,4,6,7,8,14,17,20,21,22,23) and (3,11,12,13,15,16,18,19,24,25,28) corresponding to
Figure 4. However, the results (
Figure 7) should be taken with care, because the former class includes four compounds with the constant <11111> vector (anaesthetics 4, 6, 20 and 23), for which the null standard deviation causes a correlation coefficient of
r = 1 with any local anaesthetic, which is an artifact.
Figure 7.
Splits graph for the local anaesthetics analogues of procaine.
Figure 7.
Splits graph for the local anaesthetics analogues of procaine.
A principal component analysis (PCA) [
33] has been carried out for the local anaesthetics. The importance of PCA factors
F1–5 for {
i1,
i2,
i3,
i4,
i5} is collected in
Table 4. In particular the use of only the first factor
F1 explains 35% of the variance (65% error); the combined use of the first two factors
F1–2 explains 61% of the variance (39% error); the use of the first three factors
F1–3 explains 78% of the variance (22% error).
Table 4.
Importance of the principal component analysis factors for the vector property.
Table 4.
Importance of the principal component analysis factors for the vector property.
| Factor | Eigenvalue | Percentage of variance | Cumulative percentage of variance |
|---|
| F1 | 1.73558585 | 34.71 | 34.71 |
| F2 | 1.33757290 | 26.75 | 61.46 |
| F3 | 0.81501667 | 16.30 | 77.76 |
| F4 | 0.75678743 | 15.14 | 92.90 |
| F5 | 0.35503715 | 7.10 | 100.00 |
The PCA factor loadings are shown in
Table 5.
Table 5.
Principal component analysis loadings for the vector property of local anaesthetics.a
Table 5.
Principal component analysis loadings for the vector property of local anaesthetics.a
| | PCA factor loadings | |
|---|
| Property | F1 | F2 | F3 | F4 | F5 |
|---|
| i1 | -0.058 | 0.756 | -0.109 | -0.428 | 0.480 |
| i2 | 0.518 | -0.034 | 0.767 | 0.086 | 0.367 |
| i3 | -0.453 | 0.465 | 0.544 | 0.184 | -0.499 |
| i4 | 0.371 | 0.420 | -0.315 | 0.766 | -0.006 |
| i5 | -0.621 | -0.186 | 0.065 | 0.435 | 0.621 |
The PCA
F1–5 profile for the vector property is listed in
Table 6. In particular for
F1 and
F5 variable
i5 has the greatest weight in the profile; however,
F1 cannot be reduced to three variables {
i2,
i3,
i5} without a 14% error. For
F2 variable
i1 has the greatest weight; notwithstanding,
F2 cannot be reduced to three variables {
i1,
i3,
i4} without a 4% error. For
F3 variable
i2 has the greatest weight; nevertheless,
F3 cannot be reduced to three variables {
i2,
i3,
i4} without a 2% error. For
F4 variable
i4 has the greatest weight; however,
F4 cannot be reduced to three variables {
i1,
i4,
i5} without a 4% error.
F1–2–3–4–5 can be considered as linear combinations of {
i2,
i3,
i5}, {
i1,
i3,
i4}, {
i2,
i3,
i4}, {
i1,
i4,
i5} and {
i1,
i3,
i5} with 14%, 4%, 2%, 4% and 13% errors, respectively.
Table 6.
Profile of the principal component analysis factors for the vector property.a
Table 6.
Profile of the principal component analysis factors for the vector property.a
| Factor | Percentage of i1 | Percentage of i2 | Percentage of i3 | Percentage of i4 | Percentg. of i5 |
|---|
| F1 | 0.34 | 26.82 | 20.48 | 13.77 | 38.60 |
| F2 | 57.12 | 0.11 | 21.61 | 17.68 | 3.47 |
| F3 | 1.20 | 58.84 | 29.64 | 9.89 | 0.42 |
| F4 | 18.32 | 0.73 | 3.37 | 58.65 | 18.93 |
| F5 | 23.03 | 13.49 | 24.89 | 0.00 | 38.58 |
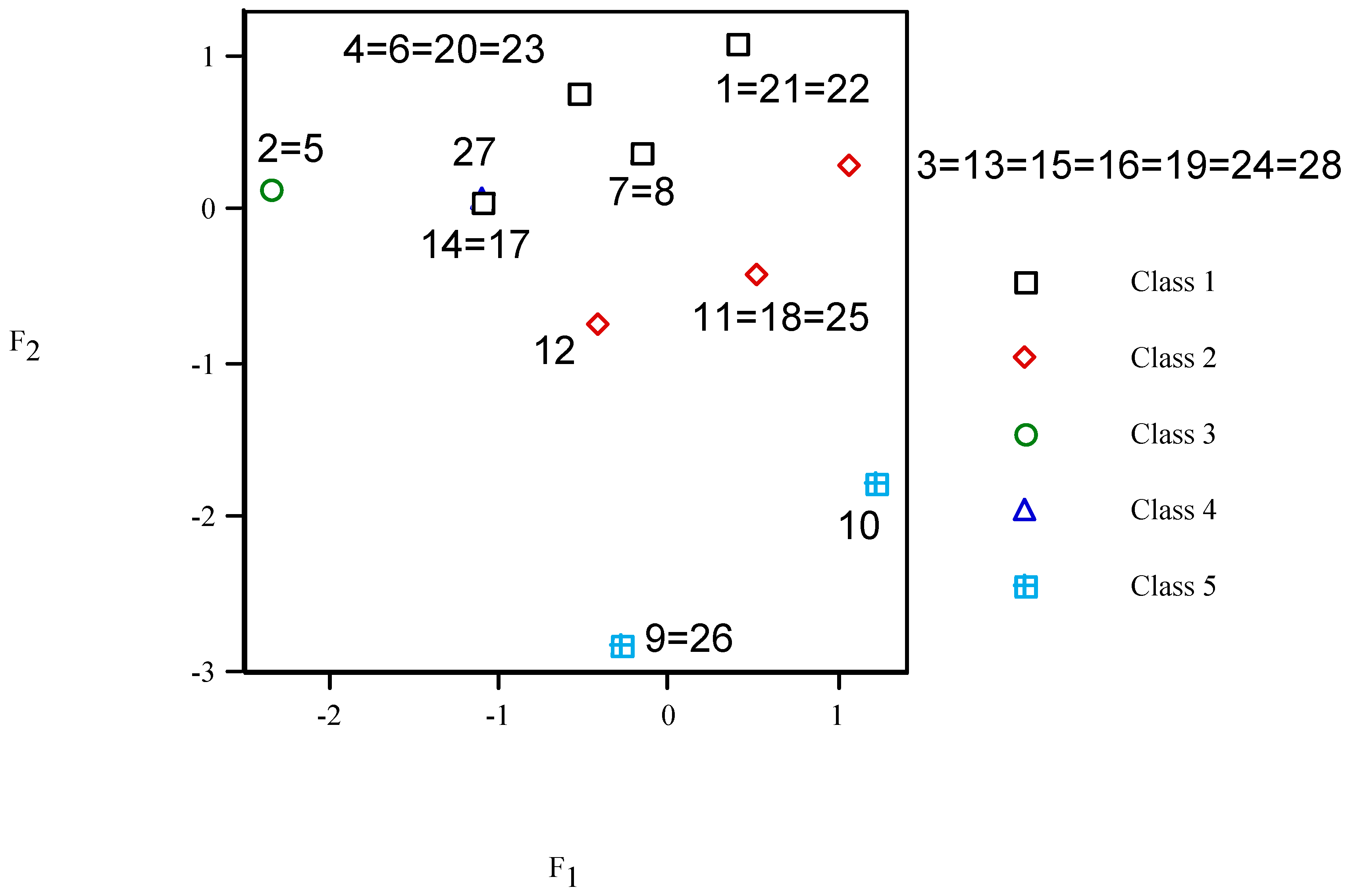
In the
F2– F1 plot (
cf.
Figure 8), those local anaesthetics analogues of procaine with the same vector property appear superimposed. In particular anaesthetic 27 (class 4) also comes out placed over compounds 14 and 17 (class 1). Five classes of anaesthetics are clearly distinguished: class 1 with 11 units (0 ≈
F1 <
F2,
top), class 2 (11 units,
F1 >
F2,
right), class 3 (2 units,
F1 <<
F2 ≈ 0,
left), class 4 (1 unit, –1 ≈
F1 <
F2 ≈ 0,
middle) and class 5 (3 units,
F1 >>
F2,
bottom). The classification is in agreement with the partial correlation diagram, dendrogram, binary trees and splits graph (
Figure 1,
Figure 2,
Figure 3,
Figure 4,
Figure 5,
Figure 6 and
Figure 7).
Figure 8.
Principal component analysis F2 vs. F1 plot for the local anaesthetics.
Figure 8.
Principal component analysis F2 vs. F1 plot for the local anaesthetics.
The recommended format for the periodic table (PT) of the local anaesthetics analogues of procaine is listed in
Table 7. Local anaesthetics are classified first by
i5, then by
i4,
i3,
i2 and, finally, by
i1. Periods of five units are assumed. Group g010 stands for <
i1,
i2,
i3> = <010>,
viz. <01001> (dibucaine, propanolol), and <01010> (dimethisoquin), group g100, for <
i1,
i2,
i3> = <100>,
i.e. <10011> (phenytoin),
etc. The local anaesthetics in the same column of
Table 7 appear close in the partial correlation diagram, dendrogram, radial trees, splits graph and PCA (
Figure 1,
Figure 2,
Figure 3,
Figure 4,
Figure 5,
Figure 6,
Figure 7 and
Figure 8).
Table 7.
Table of periodic properties for the local anaesthetics analogues of procaine.
Table 7.
Table of periodic properties for the local anaesthetics analogues of procaine.
| g010 | g100 | g101 | g110 | g111 |
|---|
| | | | diperodon, pramoxine, mexiletine | cocaine, cyclomethycaine |
| dibucaine, propanolol | | benzocaine, butamben | dyclonine | hexylcaine, piperocaine |
| dimethisoquin | | | bupivacaine, etidocaine, lidocaine, mepivacaine, prilocaine, tocainide, S-ropivacaine | benoxinate, proparacaine, propoxycaine |
| | phenytoin | | | butacaine, 2-chloroprocaine, procaine, tetracaine |
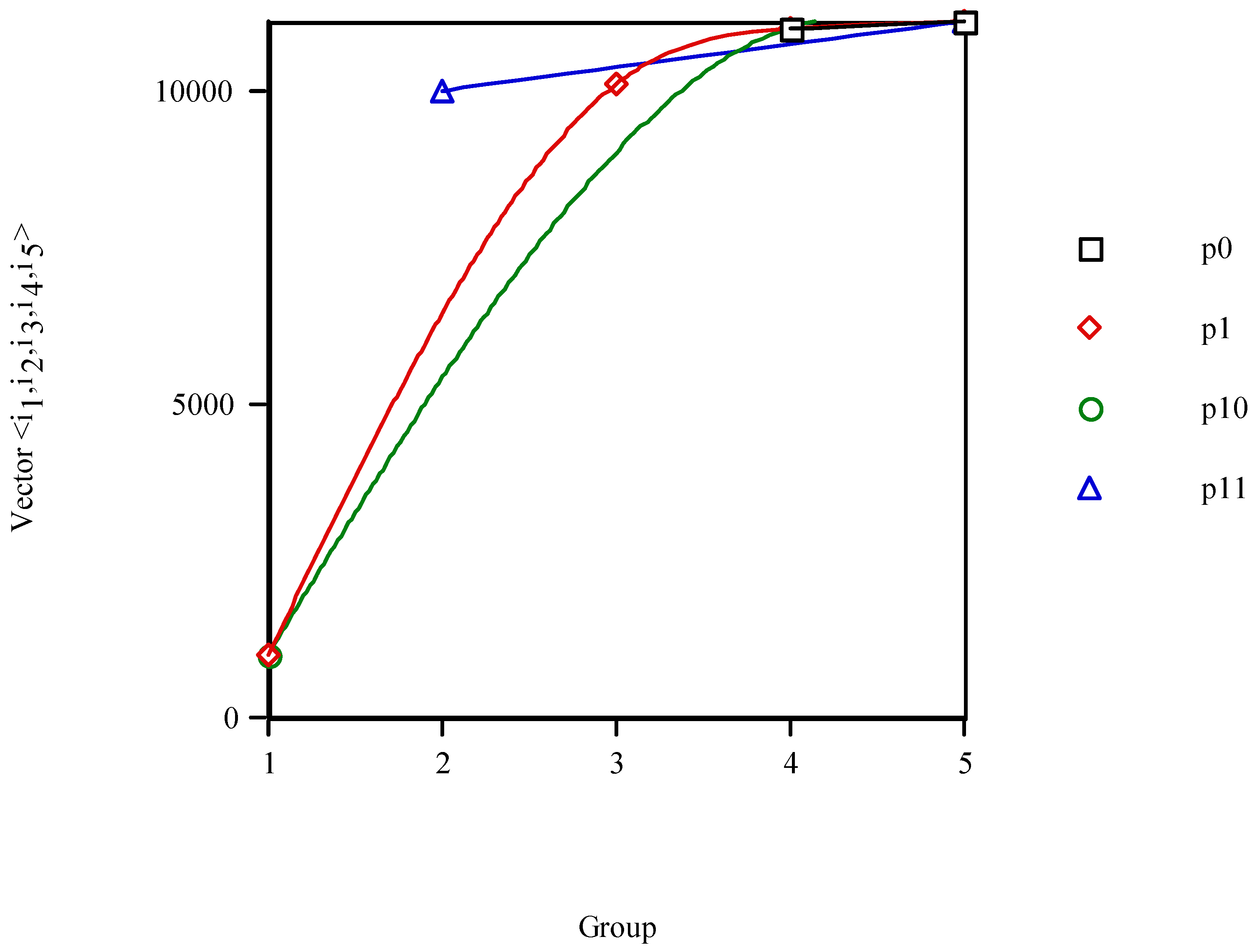
Figure 9 exhibits the variation of the vector property as a function of the structural parameters {
i1,
i2,
i3,
i4,
i5} for local anaesthetics. The lines for the structural parameters
i4 and
i5 appear superimposed, what agrees with a PT of properties with vertical groups defined by {
i1,
i2,
i3} and horizontal periods described by {
i4,
i5}.
Figure 9.
Variation of the vector property of local anaesthetics vs. counts {i1,i2,i3,i4,i5}.
Figure 9.
Variation of the vector property of local anaesthetics vs. counts {i1,i2,i3,i4,i5}.
The variation of the vector property
P = <
i1,
i2,
i3,
i4,
i5>, as a function of the number of the group in PT (
cf.
Figure 10) for local anaesthetics, reveals that the minima correspond to anaesthetics with {
i1,
i2,
i3} values of <010> (group g010). The corresponding function
P(
i1,
i2,
i3,
i4,
i5) reveals a series of
waves clearly limited by maxima or minima, which suggest a periodic behaviour that recalls the form of a trigonometric function. For <
i1,
i2,
i3,
i4,
i5> two minima are clearly shown. The distance in {
i1,
i2,
i3,
i4,
i5} units between each pair of consecutive minima is five, which coincides with the local anaesthetic sets belonging to the same group in PT and in the successive periods. The minima occupy analogous positions in the curve and are in phase. The representative points in phase should correspond to the elements of the same group in PT. For the <
i1,
i2,
i3,
i4,
i5> minima there is coherence between both representations; however, the consistency is not general. The comparison of the
waves shows two differences: (1) periods 1–2 show some sawtooth-like structures with marked discontinuities in
P(
i1,
i2,
i3,
i4,
i5); (2) periods 3–4 are also sawtooth-like although much less marked. The most characteristic points of the plot are the minima, which correspond to the anaesthetics of group g010. Their <
i1,
i2,
i3,
i4,
i5> values are not repeated as the periodic law (PL) states but decrease regularly.
Figure 10.
Variation of the vector property of local anaesthetics vs. group number.
Figure 10.
Variation of the vector property of local anaesthetics vs. group number.
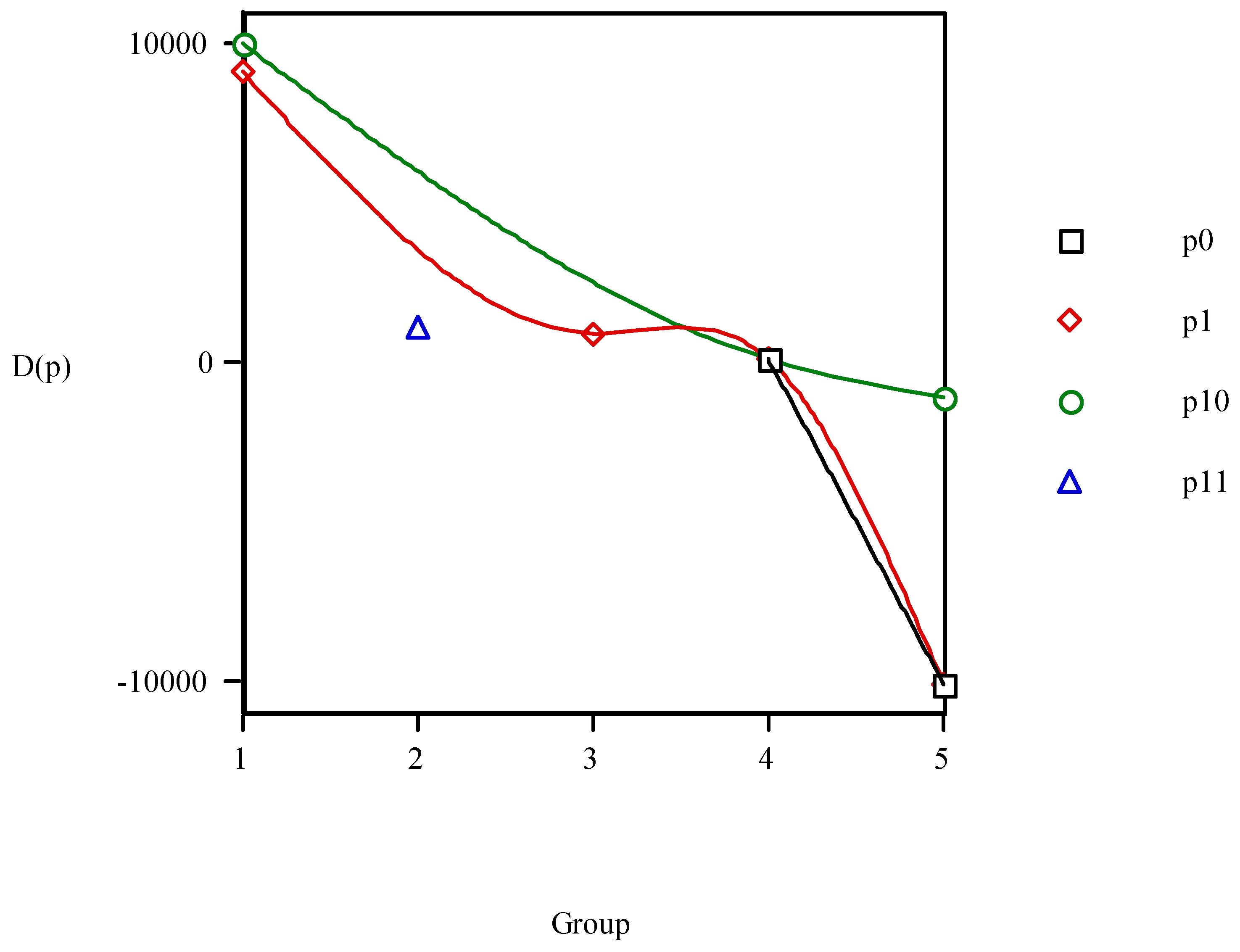
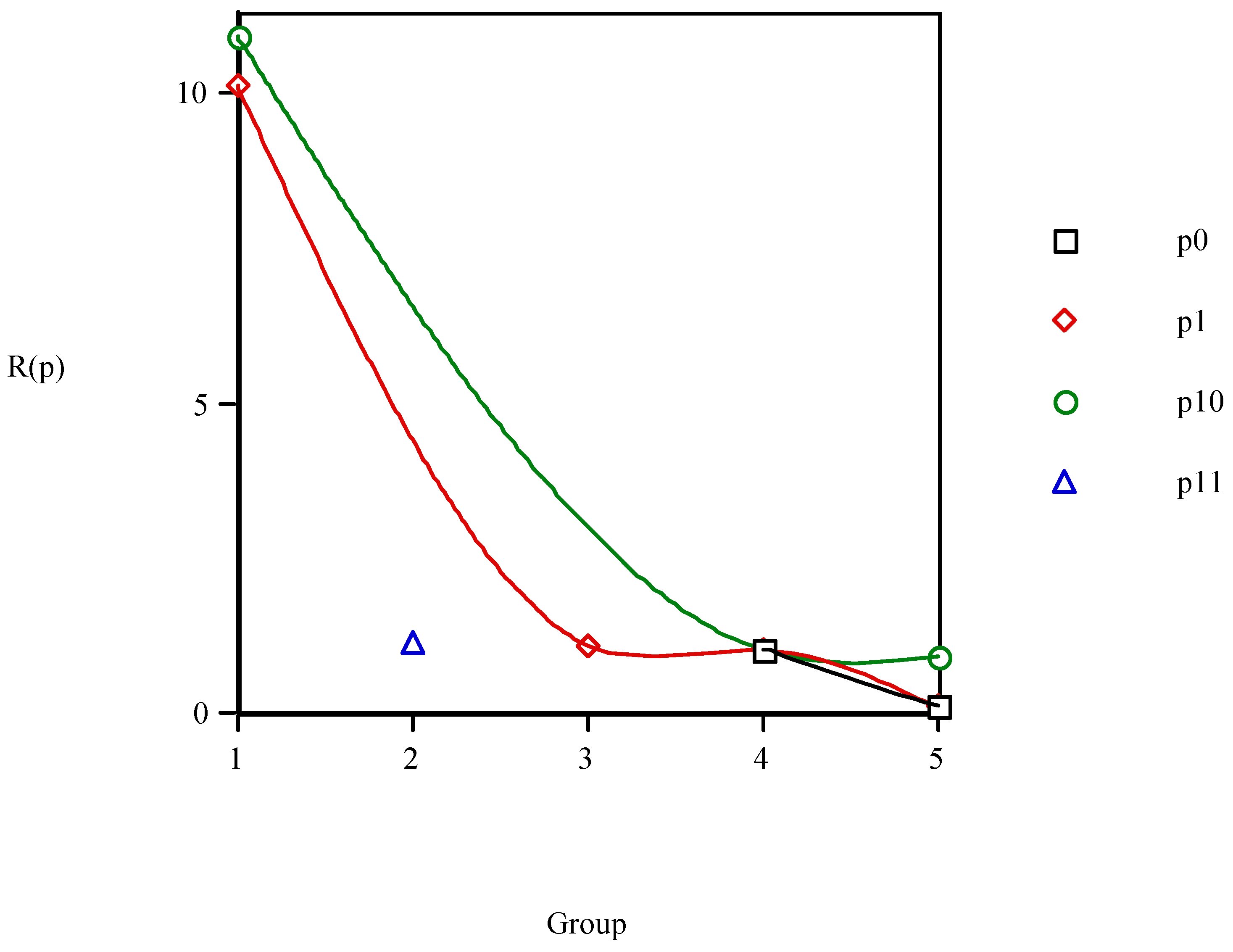
An empirical function P(i1,i2,i3,i4,i5) reproduces, with enough precision, the different <i1,i2,i3,i4,i5> values for the anaesthetics. A minimum value of a function P(p) has meaning only if it is compared with those for the former P(p–1) and later P(p+1) points, needing to fulfil:
Order relations (8) should repeat at determined intervals equal to the values of the period size and are equivalent to:
As relations (9) are valid only for minima more general others are desired for all the values of p. Therefore, the differences P(p+1) – P(p) are calculated assigning each of their values to anaesthetic p. Naming this value D(p):
Instead of D(p) the R(p) = P(p+1)/P(p) values can be taken assigning them to anaesthetic p. If PL were general, the elements belonging to the same group occupying analogous positions in the different waves would satisfy:
However, the results show that this is not the case so that PL is not general, existing some anomalies;
e.g., the variation of
D(
p)
vs. group number in
Figure 11 presents lack of coherence between the <
i1,
i2,
i3,
i4,
i5> Cartesian and PT representations. If consistency were rigorous all the points in each period would have the same sign. In general there is a trend in the points to give
D(
p) < 0 especially for the greater groups. In detail, however, there are irregularities in which the anaesthetics for successive periods are not always in phase.
Figure 11.
Variation of D(p) = P(p+1) – P(p) vs. group number. P is the vector property.
Figure 11.
Variation of D(p) = P(p+1) – P(p) vs. group number. P is the vector property.
The change of
R(
p)
vs. group number in
Figure 12 shows lack of constancy between the Cartesian and PT charts. If steadiness were exact all the points in each period would be either lower or greater than one. There is a trend in the points to give
R(
p) > 1 particularly for the smaller groups. Notwithstanding, there are incongruities in which the anaesthetics for consecutive waves are not always in phase.
Figure 12.
Variation of R(p) = P(p+1)/P(p) vs. group number. P is the vector property.
Figure 12.
Variation of R(p) = P(p+1)/P(p) vs. group number. P is the vector property.
7. Conclusions
From the present results and discussion the folllowing conclusions can be drawn.
1. Several criteria have been selected to reduce the analysis to a manageable quantity of structures from the large set of local anaesthetics. They refer to the structural parameters related with the lipophilic portion, hydrophilic portion, etc.
2. Many algorithms for classification are based on information entropy. When applying these procedures to sets of moderate size, an excessive number of results appear compatible with data, and this number suffers a combinatorial explosion. However, after the equipartition conjecture, one has a selection criterion between different variants resulting from classification between hierarchical trees. According to this conjecture, for a given charge or duty, the best configuration of a flowsheet is the one in which the entropy production is most uniformly distributed. The method avoids the problem of other methods that consider continuum variables, because for the four compounds with constant <11111> vector (anaesthetics 4, 6, 20 and 23), the null standard deviation causes a correlation coefficient of r = 1 with any local anaesthetic. The lower level classification processes show lower entropy and, therefore, may be more parsimonious.
3. In this work, an overview of an information entropy approach (based on the equipartition conjecture) to the modelling of complex data in the area of cheminformatics has been presented. Through the proposed method we intended to show that the information entropy-based modelling of complex systems can be effectively equipped with expressive representation of complex data in the form of structured representation. As a result, concerning chemical and biological problems, we have shown that predictions can be done directly from molecular structures, introducing potential benefits in the current quantitative structure–property/activity relationship (QSPR/QSAR) method. In particular, since universal approximation capabilities of the equipartition conjecture have been proved (specifically for tree-structured domains [
15]), the equipartition conjecture can be considered a general tool especially useful to deal with new tasks where the relevance of the
ad hoc molecular descriptors is unknown. More generally, the present approach can be seen as a paradigmatic example of the studies aiming at extending information entropy techniques to the treatment of various structured classes of data [
17]. Our aim here is also to propose the new approach as a general method to tackle various structured problems in the areas of cheminformatics and bionformatics. Main potential developments concern hard tasks in toxicology and bioinformatics whenever is natural to find useful structured representation of chemical/biological data.
4. The area of clustering is notoriously difficult;
e.g. although oranges and apples seem to have significant differences they are both fruit. Is a pomegranate more like an apple or is it more like an orange? When the clustering problem is poorly specified, or the variation within each cluster is greater than that between different clusters, meaningful clustering often becomes almost impossible. Progression in the development of new methods is hampered by the lack of
gold standards, against which to judge the quality of any clustering exercise. An understanding of both the chemistry and the computational methods is essential for tackling the associated
data mining tasks, without being distracted by the abundant fool’s gold. If a small number of clusters of data are easy to fit, the predictive ability of the model could be guaranteed only if the deviations inside the clusters do not diverge [
34]. As suggested by Senese
et al. [
35] in a different context, the generated clusters can be used to generate different QSAR models in order to obtain better representation of the data. Thus, clustering methods can be used to identify single QSARs representing each of them different information that can be overlooked when trying to represent all the data by only one.
5. Information entropy and principal component analyses permit classifying the local anaesthetics and agree. The ester (benzocaine, 2-chloroprocaine, procaine, tetracaine) and amide type local anaesthetics (bupivacaine, dibucaine, etidocaine, lidocaine, mepivacaine, prilocaine, S-ropivacaine) are always grouped in different classes. The agents of low potency and short duration (procaine, 2-chloroprocaine) are separated from the agents of high potency and long duration (bupivacaine, etidocaine, S-ropivacaine), while the agents of moderate potency and duration (mepivacaine, prilocaine) are classified together with the latter. The final classification is shown more precise and with lower bias. The classification model calculates in each case the contribution of signal and noise.
6. The periodic law has not the rank of the laws of physics: (1) the properties of the local anaesthetics are not repeated; perhaps, their chemical character; (2) the order relationships are repeated, with exceptions. The analysis forces the statement: The relationships that any anaesthetic p has with its neighbour p + 1 are approximately repeated for each period. Periodicity is not general; however, if a natural order of the anaesthetics is accepted the law must be phenomenological.
7. Bupivacaine cardiotoxicity results from prolonged Na+ channel dwell time of the R-, as compared with the S-, stereoisomer. Bupivacaine, like most aminoamide local anesthetics, has a chiral C atom where the amide linkage joins the hydrophilic tail. Chirality yields two steric forms (S and R) which are spatial mirror images with different receptor kinetics; commercial bupivacaine is the optically inactive racemic (RS) mixture of R- and S-bupivacaine. Ropivacaine is unique in that membrane separation synthesis exclusively yields the S-(–)-enantiomer, which is a local anesthetic with lower cardiotoxic potential than racemic bupivacaine.
8. As the options for the practitioner continue to grow, the need for studies comparing onset of action, efficacy and safety continues to be of paramount importance. A natural trend is to interchange similar anaesthetics in the composition of complex drugs (EMLA®).
 = <i1,i2,…ik,…> should be associated to each local anaesthetic i, whose components correspond to different characteristic groups of the molecule of anaesthetic, in a hierarchical order according to the expected importance of their pharmacological potency. If the m-th portion of the molecule is pharmacologically more significant for the anaesthetic effect than the k-th portion, then m < k. The components ik are “1” or “0” according to whether a similar (or identical) portion of rank k is present or absent in anaesthetic i compared with the reference anaesthetic. Our analysis includes such chemical compounds that fit the following general scheme: (lipophilic portion)–(intermediate chain)–(hydrophilic portion), since these are the most numerous and have the widest range of uses among the species used in practice of local anaesthesia [16]. The lipophilic portion normally consists of at least one phenyl radical, the hydrophilic portion is most often a secondary or tertiary amine, and the intermediate chain commonly has an ester or amide linkage [17]. It is assumed that the structural elements of a local anaesthetic molecule can be ranked, according to their contribution to anaesthetic potency, in the following order of decreasing importance: lipophilic portion > hydrophilic portion > intermediate chain > number of nitrogen atoms > number of oxygen atoms. The lipophilic portion is primarily responsible for the lipid solubility that allows diffusion across the nerve cell membrane, determining the intrinsic potency of local anaesthetics [6,7]. Both the lipophilic and hydrophilic portions determine protein-binding characteristics, which are felt to be the primary determinant of anaesthesia duration [8].
= <i1,i2,…ik,…> should be associated to each local anaesthetic i, whose components correspond to different characteristic groups of the molecule of anaesthetic, in a hierarchical order according to the expected importance of their pharmacological potency. If the m-th portion of the molecule is pharmacologically more significant for the anaesthetic effect than the k-th portion, then m < k. The components ik are “1” or “0” according to whether a similar (or identical) portion of rank k is present or absent in anaesthetic i compared with the reference anaesthetic. Our analysis includes such chemical compounds that fit the following general scheme: (lipophilic portion)–(intermediate chain)–(hydrophilic portion), since these are the most numerous and have the widest range of uses among the species used in practice of local anaesthesia [16]. The lipophilic portion normally consists of at least one phenyl radical, the hydrophilic portion is most often a secondary or tertiary amine, and the intermediate chain commonly has an ester or amide linkage [17]. It is assumed that the structural elements of a local anaesthetic molecule can be ranked, according to their contribution to anaesthetic potency, in the following order of decreasing importance: lipophilic portion > hydrophilic portion > intermediate chain > number of nitrogen atoms > number of oxygen atoms. The lipophilic portion is primarily responsible for the lipid solubility that allows diffusion across the nerve cell membrane, determining the intrinsic potency of local anaesthetics [6,7]. Both the lipophilic and hydrophilic portions determine protein-binding characteristics, which are felt to be the primary determinant of anaesthesia duration [8].
 and
and  vectors, respectively. The relation of similitude is characterized by a similarity matrix
vectors, respectively. The relation of similitude is characterized by a similarity matrix  . The similarity index between two anaesthetics
. The similarity index between two anaesthetics  = <i1, i2,… ik,…> and
= <i1, i2,… ik,…> and  = <j1, j2,… jk,…> is defined as:
= <j1, j2,… jk,…> is defined as:


 and
and  are matrices of the same type, and
are matrices of the same type, and  is the (i,j)-th element of the matrix
is the (i,j)-th element of the matrix  [18]. It can be shown that when applying this rule iteratively so that
[18]. It can be shown that when applying this rule iteratively so that  , there exists an integer n such that:
, there exists an integer n such that:  The resulting matrix
The resulting matrix  is called the stabilized similarity matrix. The importance of stabilization lies in the fact that in the classification process, it will generate a partition in disjoint classes. From now on, it is understood that the stabilized matrix is used and designated by
is called the stabilized similarity matrix. The importance of stabilization lies in the fact that in the classification process, it will generate a partition in disjoint classes. From now on, it is understood that the stabilized matrix is used and designated by  . The grouping rule is the following: i and j are assigned to the same class if rij(n) ≥ b. The class of i noted
. The grouping rule is the following: i and j are assigned to the same class if rij(n) ≥ b. The class of i noted  is the set of species j that satisfies the rule rij(n) ≥ b. The matrix of classes is:
is the set of species j that satisfies the rule rij(n) ≥ b. The matrix of classes is:

 (similarly for t and
(similarly for t and  ). Rule (3) means finding the largest similarity index between species of two different classes.
). Rule (3) means finding the largest similarity index between species of two different classes. is:
is:
 the matrix of similarity at the grouping level b. The information entropy satisfies the following properties.
the matrix of similarity at the grouping level b. The information entropy satisfies the following properties.if rij = 0 or rij = 1.
is maximum if rij = 0.5, i.e. when the imprecision is maximum.
for any b, i.e. classification leads to a loss of entropy.
if b1 < b2, i.e. the entropy is a monotone function of the grouping level b.


 obtained for equal weights a1 = a2 = … = a and for an arbitrary number of fictious properties. Next consider the same set of species as in the good classification and the actual properties. The similarity degree rij is then computed with Equation (1) giving the matrix
obtained for equal weights a1 = a2 = … = a and for an arbitrary number of fictious properties. Next consider the same set of species as in the good classification and the actual properties. The similarity degree rij is then computed with Equation (1) giving the matrix  . The number of properties for
. The number of properties for  and
and  may differ. The learning procedure consists in trying to find classification results for
may differ. The learning procedure consists in trying to find classification results for  as close as possible to the good classification. The first weight a1 is taken constant and only the following weights a2, a3,… are subjected to random variations. A new similarity matrix is obtained using Equation (1) and the new weights. The distance between the partitions in classes characterized by
as close as possible to the good classification. The first weight a1 is taken constant and only the following weights a2, a3,… are subjected to random variations. A new similarity matrix is obtained using Equation (1) and the new weights. The distance between the partitions in classes characterized by  and
and  is given by:
is given by:



 = (1,21,22)(2,5)(3,13,15,16,19,24,28)(4,6,20,23)(7,8)(9,26)(10)(11,18,25)(12)(14,17)(27)
= (1,21,22)(2,5)(3,13,15,16,19,24,28)(4,6,20,23)(7,8)(9,26)(10)(11,18,25)(12)(14,17)(27) = 58.86. The dendrogram (binary tree) [23,24] matching to <i1,i2,i3,i4,i5> and
= 58.86. The dendrogram (binary tree) [23,24] matching to <i1,i2,i3,i4,i5> and  is illustrated [25] in Figure 2. It provides a binary taxonomy of Table 1, which separates the same 11 classes. In particular, the ester (benzocaine, 2-chloroprocaine, procaine, tetracaine) and amide local anaesthetics (bupivacaine, dibucaine, etidocaine, lidocaine, mepivacaine, prilocaine, S-ropivacaine) are always grouped in different classes. The agents of low potency and short duration (procaine, 2-chloroprocaine) are separated from the agents of high potency and long duration (bupivacaine, etidocaine, S-ropivacaine), while the agents of moderate potency and duration (mepivacaine, prilocaine) are classified together with the latter. Those anaesthetics belonging to the same class appear higly correlated in the partial correlation diagram (Figure 1), in agreement with previous results obtained for the first 27 entries in Table 1 [17].
is illustrated [25] in Figure 2. It provides a binary taxonomy of Table 1, which separates the same 11 classes. In particular, the ester (benzocaine, 2-chloroprocaine, procaine, tetracaine) and amide local anaesthetics (bupivacaine, dibucaine, etidocaine, lidocaine, mepivacaine, prilocaine, S-ropivacaine) are always grouped in different classes. The agents of low potency and short duration (procaine, 2-chloroprocaine) are separated from the agents of high potency and long duration (bupivacaine, etidocaine, S-ropivacaine), while the agents of moderate potency and duration (mepivacaine, prilocaine) are classified together with the latter. Those anaesthetics belonging to the same class appear higly correlated in the partial correlation diagram (Figure 1), in agreement with previous results obtained for the first 27 entries in Table 1 [17].
 = (1,4,6,7,8,14,17,20,21,22,23)(2,5)(3,11,12,13,15,16,18,19,24,25,28)(9,10,26)(27)
= (1,4,6,7,8,14,17,20,21,22,23)(2,5)(3,11,12,13,15,16,18,19,24,25,28)(9,10,26)(27)  = 12.20. The radial tree matching to <i1,i2,i3,i4,i5> and
= 12.20. The radial tree matching to <i1,i2,i3,i4,i5> and  (cf. Figure 4) separates the same five classes, in agreement with the partial correlation diagram, dendrogram, binary tree (Figure 1, Figure 2 and Figure 3) and previous results obtained for the first 27 entries in Table 1 [17]. A high degree of similarity is found for Entries 9 and 26 (i.e. dibucaine and propanolol), as well as Entries 2 and 5 (i.e. benzocaine and butamben). Again, the ester and amide local anaesthetics are grouped in different classes; the agents of low potency and short duration are separated from the agents of high–medium potency and long–medium duration. The lower level b2 classification process shows lower entropy and, therefore, may be more parsimonious. The classification model divides the point process into two components, viz. signal, and noise; the lower-level b2 may have greater signal-to-noise ratio than the higher-level b1 classification process. Naturally, Entries 4, 6, 20 and 23 (i.e. butacaine, 2-chloroprocaine, procaine and tetracaine) belong to the same class at any grouping level b, except at the highest level above which each class contains only one species. A detailed classification at level b1 into 11 classes, and a less detailed classification at a lower level b2 into five classes can be selected, taking into account the amount of entropy variation.
(cf. Figure 4) separates the same five classes, in agreement with the partial correlation diagram, dendrogram, binary tree (Figure 1, Figure 2 and Figure 3) and previous results obtained for the first 27 entries in Table 1 [17]. A high degree of similarity is found for Entries 9 and 26 (i.e. dibucaine and propanolol), as well as Entries 2 and 5 (i.e. benzocaine and butamben). Again, the ester and amide local anaesthetics are grouped in different classes; the agents of low potency and short duration are separated from the agents of high–medium potency and long–medium duration. The lower level b2 classification process shows lower entropy and, therefore, may be more parsimonious. The classification model divides the point process into two components, viz. signal, and noise; the lower-level b2 may have greater signal-to-noise ratio than the higher-level b1 classification process. Naturally, Entries 4, 6, 20 and 23 (i.e. butacaine, 2-chloroprocaine, procaine and tetracaine) belong to the same class at any grouping level b, except at the highest level above which each class contains only one species. A detailed classification at level b1 into 11 classes, and a less detailed classification at a lower level b2 into five classes can be selected, taking into account the amount of entropy variation.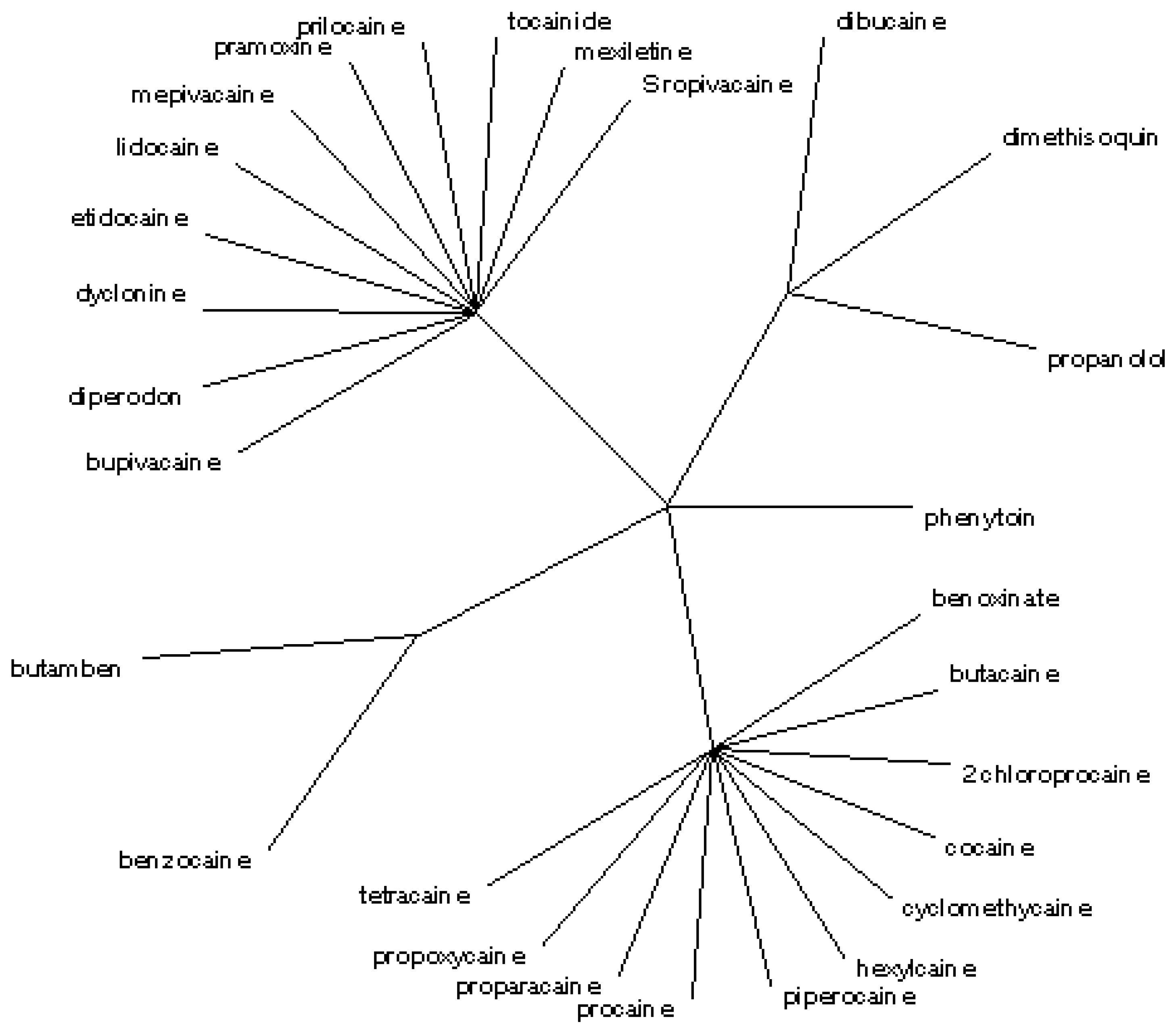
 (cf. Figure 5) separates the same five and 11 classes, in agreement with the partial correlation diagram, dendrogram, binary trees (Figure 1, Figure 2, Figure 3 and Figure 4) and previous results obtained for the first 27 entries in Table 1 [17]. Again, the ester and amide local anaesthetics are grouped in different classes; the agents of low potency and short duration are separated from the agents of high–medium potency and long–medium duration.
(cf. Figure 5) separates the same five and 11 classes, in agreement with the partial correlation diagram, dendrogram, binary trees (Figure 1, Figure 2, Figure 3 and Figure 4) and previous results obtained for the first 27 entries in Table 1 [17]. Again, the ester and amide local anaesthetics are grouped in different classes; the agents of low potency and short duration are separated from the agents of high–medium potency and long–medium duration.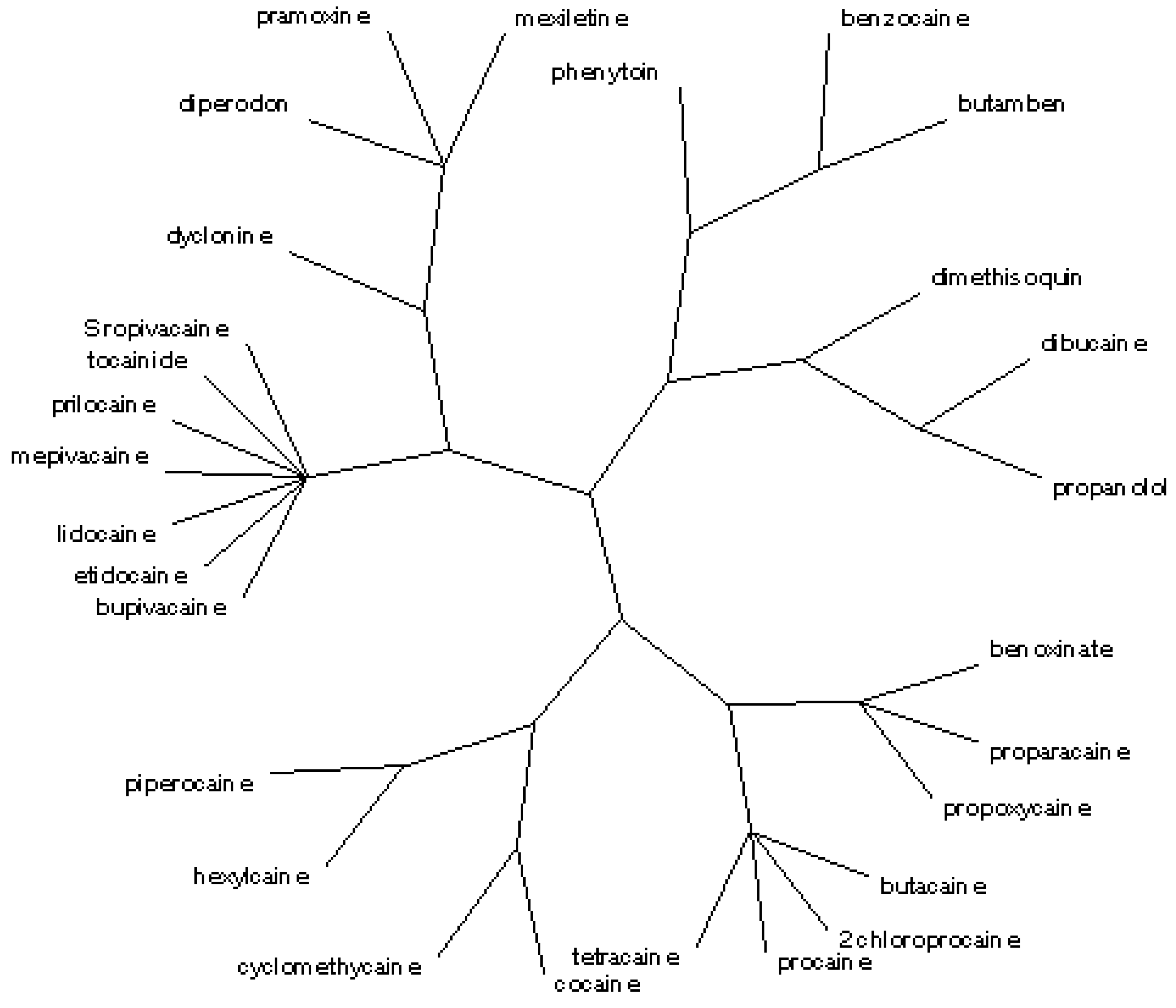
 classes (1,4,6,7,8,14,17,20,21,22,23) and (3,11,12,13,15,16,18,19,24,25,28) corresponding to Figure 4. However, the results (Figure 7) should be taken with care, because the former class includes four compounds with the constant <11111> vector (anaesthetics 4, 6, 20 and 23), for which the null standard deviation causes a correlation coefficient of r = 1 with any local anaesthetic, which is an artifact.
classes (1,4,6,7,8,14,17,20,21,22,23) and (3,11,12,13,15,16,18,19,24,25,28) corresponding to Figure 4. However, the results (Figure 7) should be taken with care, because the former class includes four compounds with the constant <11111> vector (anaesthetics 4, 6, 20 and 23), for which the null standard deviation causes a correlation coefficient of r = 1 with any local anaesthetic, which is an artifact.