Prediction of Environmental Properties for Chlorophenols with Posetic Quantitative Super-Structure/Property Relationships (QSSPR)
Abstract
:1. Introduction
2. The Reaction Poset Diagram for Phenol Substitution
3. Experimental Data
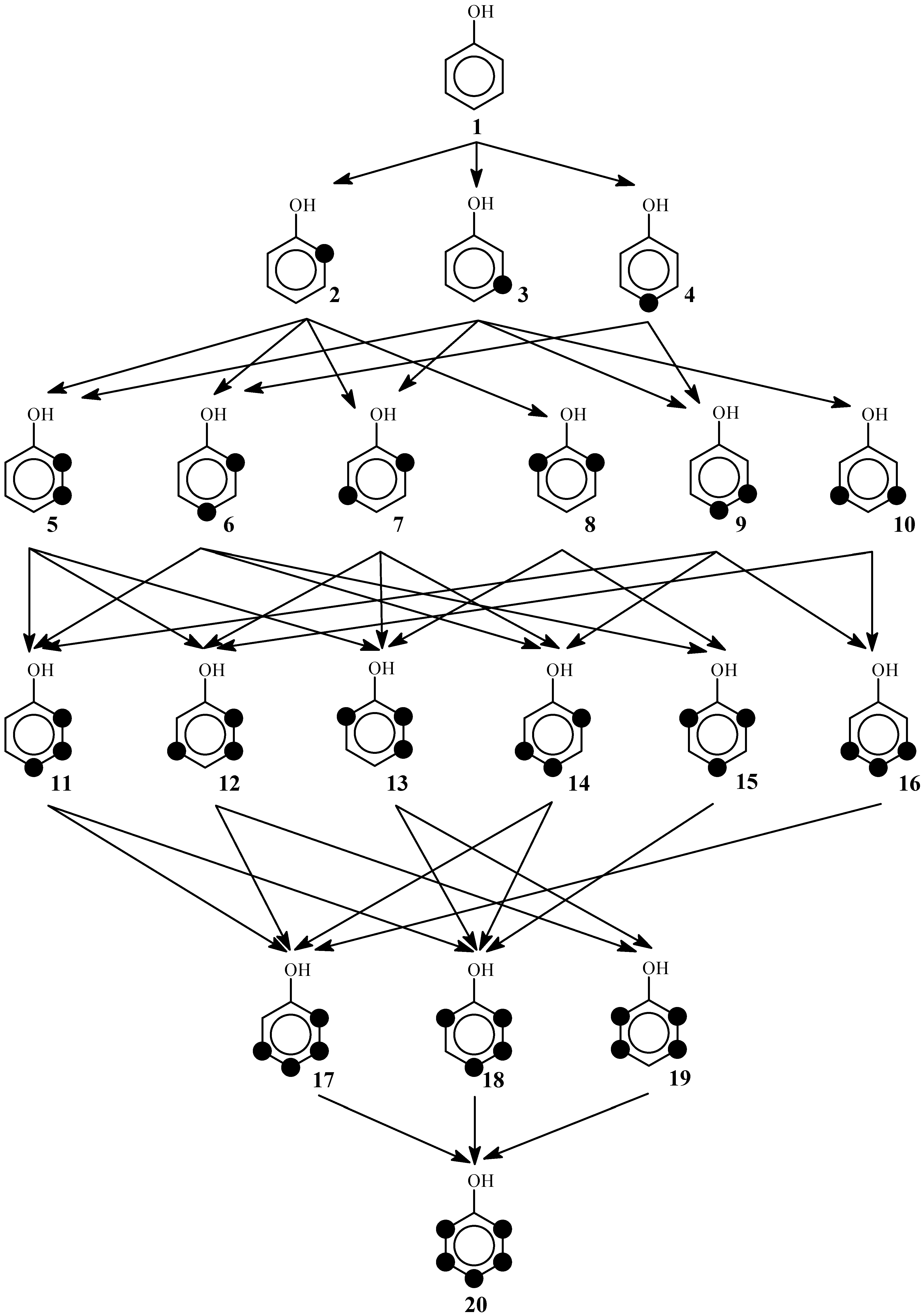
4. Posetic Methodology
4.1 Posetic Applications in General
4.2 Reaction Poset Super-Structures
4.3 Posetic QSSPR and QSSAR Modelling
4.4 Average-Poset Model

4.5 Splinoid Poset Model




 . Then, the vector
. Then, the vector  that contains the predictions for the unknown property values aα is computed from:
that contains the predictions for the unknown property values aα is computed from:

 , but they are complicit in the derivation of this formula for
, but they are complicit in the derivation of this formula for  . The present formula gives
. The present formula gives  in terms of the poset structure, and thence completes the splinoid QSSPR algorithm, which turns out to give a robust model in accommodating a diversity of missing values for several compounds (which may possibly even be adjacent). This is a significant advantage of the splinoid model, which uses the topology of the Hasse diagram to generate a response network for the investigated property. To achieve comparison with the results from the other poset QSSPR models, we have used the splinoid model in the leave-one-out cross-validation procedure.
in terms of the poset structure, and thence completes the splinoid QSSPR algorithm, which turns out to give a robust model in accommodating a diversity of missing values for several compounds (which may possibly even be adjacent). This is a significant advantage of the splinoid model, which uses the topology of the Hasse diagram to generate a response network for the investigated property. To achieve comparison with the results from the other poset QSSPR models, we have used the splinoid model in the leave-one-out cross-validation procedure.4.6 Cluster-Expansion Model

5. Results and Discussions

| No. | Compound | Splinoid model | Cluster-expansion |
| 1 | P | 1.72 | 1.72 |
| 2 | 2-ClP | 2.60 | 2.23 |
| 3 | 3-ClP | 2.54 | 2.78 |
| 4 | 4-ClP | 2.42 | 2.81 |
| 5 | 2,3-Cl2P | 2.65 | 3.25 |
| 6 | 2,4-Cl2P | 2.74 | 2.95 |
| 7 | 2,5-Cl2P | 2.87 | 2.68 |
| 8 | 2,6-Cl2P | 2.78 | 2.51 |
| 9 | 3,4-Cl2P | 3.09 | 3.14 |
| 10 | 3,5-Cl2P | 2.92 | 2.71 |
| 11 | 2,3,4-Cl3P | 3.32 | 3.43 |
| 12 | 2,3,5-Cl3P | 3.35 | 3.09 |
| 13 | 2,3,6-Cl3P | 3.24 | 2.99 |
| 14 | 2,4,5-Cl3P | 3.36 | 3.12 |
| 15 | 2,4,6-Cl3P | 3.03 | 2.95 |
| 16 | 3,4,5-Cl3P | 3.56 | 3.48 |
| 17 | 2,3,4,5-Cl4P | 4.12 | 3.97 |
| 18 | 2,3,4,6-Cl4P | 3.82 | 3.74 |
| 19 | 2,3,5,6-Cl4P | 3.92 | 3.58 |
| 20 | Cl5P | 4.52 | 4.96 |
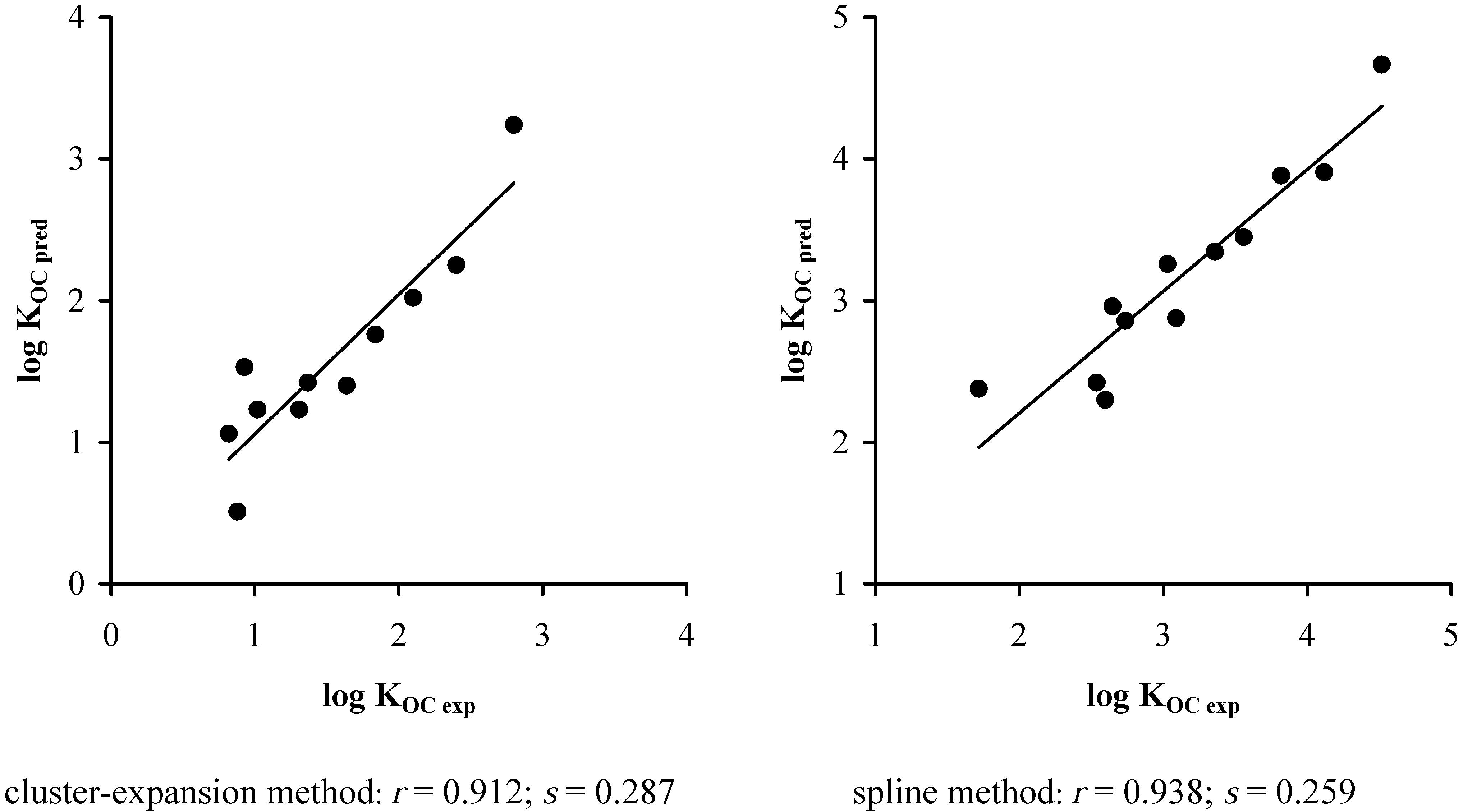



3. Conclusions
Acknowledgements
References and Notes
- Kaise, K. L. E. Organic Contaminants in the Environment: Research Progress and Needs. Environ. Intern. 1984, 10, 241–250. [Google Scholar] [CrossRef]
- Kieth, L. H.; Telliard, W. A. Priority Pollutants, Part I: A Perspective View. Envir. Sci. Technol. 1979, 13, 416–423. [Google Scholar] [CrossRef]
- Guo, R.; Liang, X.; Chen, J.; Wu, W.; Zhang, Q.; Martens, D.; Kettrup, A. Prediction of Soil Organic Carbon Partition Coefficients by Soil Column Liquid Chromatography. J. Chromatogr. A 2004, 1035, 31–36. [Google Scholar] [CrossRef]
- Gramatica, P.; Corradi, M.; Consonni, V. Modelling and Prediction of Soil Sorption Coeffcients of Non-Ionic Organic Pesticides by Molecular Descriptors. Chemosphere 2000, 41, 763–777. [Google Scholar] [CrossRef]
- Chu, W.; Chan, K. H. The Prediction of Partitioning Coefficients for Chemicals Causing Environmental Concern. Sci. Tot. Environ. 2000, 248, 1–10. [Google Scholar] [CrossRef]
- Chiou, C. T.; Schmedding, D. W.; Manes, M. Improved Prediction of Octanol-Water Partition Coefficients from Liquid-Solute Water Solubilities and Molar Volumes. Environ. Sci. Technol. 2005, 39, 8840–8846. [Google Scholar] [CrossRef]
- Sabljić, A.; Güsten, H.; Verhaar, H.; Hermens, J. QSAR Modelling of Soil Sorption. Improvements and Systematics of log Koc, vs. log Kow Correlations. Chemosphere 1995, 31, 4489–4514. [Google Scholar] [CrossRef]
- Briggs, G. G. Theoretical and Experimental Relationships Between Soil Adsorption, Gctanol-Water Partition Coefficients, Water Solubilities, Bioconcentration Factors, and the Parachor. J. Agric. Food Chem. 1981, 29, 1050–1059. [Google Scholar] [CrossRef]
- Sabljić, A. On the Prediction of Soil Sorption Coefficients of Organic Pollutants from Molecular Structure: Application of Molecular Topology Model. Environ. Sci. Technol. 1987, 21, 358–366. [Google Scholar] [CrossRef]
- Baker, J. R.; Mihelcic, J. R.; Sabljić, A. Reliable QSAR for Estimating Koc for Persistent Organic Pollutants: Correlation with Molecular Connectivity Indices. Chemosphere 2001, 45, 213–221. [Google Scholar] [CrossRef]
- Yang, K.; Zhu, L.; Lou, B.; Chen, B. Correlations of Nonlinear Sorption of Organic Solutes with Soil/Sediment Physicochemical Properties. Chemosphere 2005, 61, 116–128. [Google Scholar] [CrossRef]
- Chiou, C. T.; Schmedding, D. W.; Manes, M. Partitioning of Organic Compounds in Octanol-Water Systems. Environ. Sci. Technol. 1982, 16, 4–10. [Google Scholar]
- http://www.atsdr.cdc.gov/toxprofiles/tp107.html Toxicological Profile for Chlorophenols.
- Nichkova, M.; Marco, M. P. Biomonitoring Human Exposure to Organohalogenated Substances by Measuring Urinary Chlorophenols Using a High-Throughput Screening (HTS) Immunochemical Method. Environ. Sci. Technol. 2006, 40, 2469–2477. [Google Scholar] [CrossRef]
- Zhao, F.; Mayura, K.; Hutchinson, R.W.; Lewis, R. P.; Burghardt, R. C.; Phillips, T. D. Developmental Toxicity and Structure-Activity Relationships of Chlorophenols Using Human Embryonic Palatal Mesenchymal Cells. Toxicol. Lett. 1995, 78, 35–42. [Google Scholar]
- Chen, J.; Zhang, F.; Yu, F.; Zhang, J. Cytotoxic Effects of Environmentally Relevant Chlorophenols on L929 Cells and Their Mechanisms. Cell Biol. Toxicol. 2004, 20, 183–196. [Google Scholar] [CrossRef]
- Wang, Y. –J.; Lee, C. -C.; Chang, W. –C.; Liou, H. –B.; Ho, Y. –S. Oxidative Stress and Liver Toxicity in Rats and Human Hepatoma Cell Line Induced by Pentachlorophenol and its Major Metabolite Tetrachlorohydroquinone. Toxicol. Lett. 2001, 122, 157–169. [Google Scholar] [CrossRef]
- Kukkonen, J. V. K. Lethal Body Residue of Chlorophenols and Mixtures of Chlorophenols in Benthic Organisms. Arch. Environ. Contam. Toxicol. 2002, 43, 214–220. [Google Scholar] [CrossRef]
- Buikema, A. L., Jr.; McGinniss, M. J.; Cairns, J., Jr. Phenolics in Aquatic Ecosystems: A Selected Review of Recent Literature. Marine Environ. Res. 1979, 2, 87–181. [Google Scholar] [CrossRef]
- Ahlborg, U. G.; Thunberg, T. M. Chlorinated Phenols: Occurrence, Toxicity, Metabolism, and Environmental Impact. CRC Crit. Rev. Toxicol. 1980, 7, 1–35. [Google Scholar] [CrossRef]
- Czaplicka, M. Sources and Transformations of Chlorophenols in the Natural Environment. Sci. Tot. Environ. 2004, 322, 21–39. [Google Scholar] [CrossRef]
- Klein, D. J. Similarity and Dissimilarity in Posets. J. Math. Chem. 1995, 18, 321–348. [Google Scholar] [CrossRef]
- Klein, D. J.; Babić, D. Partial Orderings in Chemistry. J. Chem. Inf. Comput. Sci. 1997, 37, 656–671. [Google Scholar] [CrossRef]
- Klein, D. J. Prolegomenon on Partial Orderings in Chemistry. Commun. Math. Comput. Chem. (MATCH) 2000, 42, 7–21. [Google Scholar]
- Klein, D. J.; Bytautas, L. Directed Reaction Graphs as Posets. Commun. Math. Comp. Chem. (MATCH) 2000, 42, 261–289. [Google Scholar]
- Ivanciuc, T.; Klein, D. J. Parameter-Free Structure-Property Correlation via Progressive Reaction Posets for Substituted Benzenes. J. Chem. Inf. Comput. Sci. 2004, 44, 610–617. [Google Scholar] [CrossRef]
- Došlić, T.; Klein, D. J. Splinoid Interpolation on Finite Posets. J. Comput. Appl. Math. 2005, 177, 175–185. [Google Scholar] [CrossRef]
- Klein, D. J. Chemical Graph-Theoretic Cluster Expansions. Int. J. Quantum Chem., Quantum Chem. Symp. 1986, 20, 153–171. [Google Scholar] [CrossRef]
- Schmalz, T. G.; Živković, T.; Klein, D. J. Cluster Expansion of the Hückel Molecular Energy for Acyclics: Applications to pi Resonance Theory. Math Chem. Comp. 1987, 54, 173–190. [Google Scholar]
- Klein, D. J.; Schmalz, T. G.; Bytautas, L. Chemical Sub-Structural Cluster Expansions for Molecular Properties. SAR QSAR Environ. Res. 1999, 10, 131–156. [Google Scholar] [CrossRef]
- Ivanciuc, T.; Klein, D. J.; Ivanciuc, O. Posetic Cluster Expansion for Substitution–Reaction Diagrams and its Application to Cyclobutane. J. Math. Chem. 2006. web release. [Google Scholar]
- Ivanciuc, T.; Ivanciuc, O.; Klein, D. J. Posetic Quantitative Superstructure/Activity Relationships (QSSARs) for Chlorobenzenes. J. Chem. Inf. Model. 2005, 45, 870–879. [Google Scholar] [CrossRef]
- Ivanciuc, T.; Ivanciuc, O.; Klein, D.J. Modeling the Bioconcentration Factors and Bioaccumulation Factors of Polychlorinated Biphenyls with Posetic Quantitative Super-Structure/Activity Relationships (QSSAR). Molecular Diversity 2006, 10, 133–145. [Google Scholar]
- Arcand, Y.; Hawari, J.; Guiot, S. R. Solubility of Pentachlorophenol in Aqueous Solutions: The pH Effect. Wat. Res. 1995, 29, 131–136. [Google Scholar] [CrossRef]
- Diez, M. C.; Mora, M. L.; Videla, S. Adsorption of Phenolic Compounds and Color from Bleached Kraft Mill Effluent Using Allophanic Compounds. Water Res. 1999, 33, 125–130. [Google Scholar] [CrossRef]
- Xie, T. M.; Hulthe, B.; Folestad, S. Determination of Partition Coefficients of Chlorinated Phenols, Guaiacols and Catechols by Shake-Flask GC and HPLC. Chemosphere 1984, 13, 445–459. [Google Scholar]
- Shiu, W.-Y.; Ma, K.-C.; Varhaníčková, D.; Mackay, D. Chlorophenols and Alkylphenols: A Review and Correlation of Environmentally Relevant Properties and Fate in an Evaluative Environment. Chemosphere 1995, 29, 1155–1224. [Google Scholar]
- Saçan, M. T.; Balcioğlu, I. A. Prediction of the Soil Sorption Coefficient of Organic Pollutants by the Characteristic Root Index Model. Chemosphere 1996, 32, 1993–2001. [Google Scholar] [CrossRef]
- Brüggemann, R.; Schwaiger, J.; Negele, R. D. Applying Hasse Diagram Technique for the Evaluation of Toxicological Fish Tests. Chemosphere 1995, 30, 1767–1780. [Google Scholar] [CrossRef]
- Brüggemann, R.; Bartel, H. G. A Theoretical Concept to Rank Environmentally Significant Chemicals. J. Chem. Inf. Comput. Sci. 1999, 39, 211–217. [Google Scholar] [CrossRef]
- Pudenz, S.; Brüggemann, R.; Luther, B.; Kaune, A.; Kreimes, K. An Algebraic/Graphical Tool to Compare Ecosystems with Respect to Their Pollution V: Cluster Analysis and Hasse Diagrams. Chemosphere 2000, 40, 1373–1382. [Google Scholar] [CrossRef]
- Brüggemann, R.; Münzer, B.; Halfon, E. An Algebraic/Graphical Tool to Compare Ecosystems with Respect to Their Pollution - The German River "Elbe" as an Example - I: Hasse-Diagrams. Chemosphere 1994, 28, 863–872. [Google Scholar] [CrossRef]
- Brüggemann, R.; Pundez, S.; Carlsen, L.; Sørensen, P. B.; Thomsen, M.; Mishra, R. K. The Use of Hasse Diagrams as a Potential Approach for Inverse QSAR. SAR QSAR Environ. Res. 2001, 11, 473–487. [Google Scholar] [CrossRef]
- Carlsen, L.; Sørensen, P. B.; Thomsen, M.; Brüggemann, R. QSAR's Based on Partial Order Ranking. SAR QSAR Environ. Res. 2002, 13, 153–165. [Google Scholar] [CrossRef]
- Lerche, D.; Sørensen, P. B.; Larsen, H. L.; Carlsen, L.; Nielsen, O. J. Comparison of the Combined Monitoring-Based and Modelling-Based Priority Setting Scheme with Partial Order Theory and Random Linear Extensions for Ranking of Chemical Substances. Chemosphere 2002, 49, 637–649. [Google Scholar] [CrossRef]
- Lerche, D.; Sørensen, P. B. Evaluation of the Ranking Probabilities for Partial Orders Based on Random Linear Extension. Chemosphere 2003, 53, 981–992. [Google Scholar] [CrossRef]
- Lerche, D.; Matsuzaki, S. Y.; Sørensen, P. B.; Carlsen, L.; Nielsen, O. J. Ranking of Chemical Substances Based on the Japanese Pollutant Release and Transfer Register Using Partial Order Theory and Random Linear Extensions. Chemosphere 2004, 55, 1005–1025. [Google Scholar] [CrossRef]
- Sørensen, P. B.; Mogensen, B. B.; Carlsen, L.; Thomsen, M. The Influence on Partial Order Ranking from Input Parameter Uncertainty: Definition of a Robustness Parameter. Chemosphere 2000, 41, 595–601. [Google Scholar] [CrossRef]
- Brüggemann, R.; Carlsen, L. Partial Order in Environmental Sciences and Chemistry; Springer, 2006. [Google Scholar]
- Rival, I. Ordered Sets. In Proceedings of the NATO Advanced Study Institute held at Banff, Canada, Dordecht Holland; D. Reidel Pub. Co.: Boston; Hingham, 1982. [Google Scholar]
- Rota, G. On the Foundation of Combinatorial Theory I, Theory of Möbius Functions. Z. Wahr. Verw. Gebiete 1964, 2, 340–368. [Google Scholar] [CrossRef]
© 2006 by MDPI (http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.
Share and Cite
Ivanciuc, T.; Ivanciuc, O.; Klein, D.J. Prediction of Environmental Properties for Chlorophenols with Posetic Quantitative Super-Structure/Property Relationships (QSSPR). Int. J. Mol. Sci. 2006, 7, 358-374. https://0-doi-org.brum.beds.ac.uk/10.3390/i7090358
Ivanciuc T, Ivanciuc O, Klein DJ. Prediction of Environmental Properties for Chlorophenols with Posetic Quantitative Super-Structure/Property Relationships (QSSPR). International Journal of Molecular Sciences. 2006; 7(9):358-374. https://0-doi-org.brum.beds.ac.uk/10.3390/i7090358
Chicago/Turabian StyleIvanciuc, Teodora, Ovidiu Ivanciuc, and Douglas J. Klein. 2006. "Prediction of Environmental Properties for Chlorophenols with Posetic Quantitative Super-Structure/Property Relationships (QSSPR)" International Journal of Molecular Sciences 7, no. 9: 358-374. https://0-doi-org.brum.beds.ac.uk/10.3390/i7090358





