Introduction
Nanoscale flow studies are important in physiology, medicine and for design of nanoscale devices, etc. Molecular dynamic simulation (MDS) is used to calculate nanoscale flow problems because the continuum model is no longer valid when the dimensions of flow systems approach the molecular size. Good reviews regarding the models and solution methods of nanoscale flow problems have been published [
1,
2]. In many papers, i.e. by Travis
et al. [
3,
4], Thompson and Robbins [
5], Heinbuch and Fischer [
6], MDS methods were applied to resolve nanoscale flow problems, particularly for the study of the boundary slip phenomena. 2-D and 3-D pressure driven channel flow problems were also investigated using the MDS method. In most papers the fluid was liquid argon and the Lennard-Jones potential was used to describe the intermolecular interactions. Usually the Couette or Poiseuille steady flow was considered to illustrate the effectiveness of the MDS method. Travis
et al. [
3,
4] found that if the pore width was less than five molecular diameters, the Navier-Stokes (NS) equations break down. Travis
et al. also reported [
3] that when the channel width equals 5.1 molecular diameters, the solution given by the molecular dynamics approach deviates significantly from the NS equations solution, whereas when the channel width equals 10.2 molecular diameters, the molecular dynamics’ solution is similar to that of the Navier-Stokes equations. This means that when the channel width is very small the NS solution is meaningless and we should use molecular dynamics to simulate it. Zhang
et al. [
7] calculated a confined fluid with a nonequilibrium MDS method and discussed the phenomena of constant pore size and constant load. Thompson and Robbins [
5] simulated boundary slips with different solid wall density and interaction strength parameters. They found that the boundary slip could be observed only for very weak fluid-wall interactions. Similar problems were also studied by Koplik
et al. [
8] and Koplik and Banavar [
9]. Todd
et al. [
10] introduced an effective viscosity method to deal with the inhomogeneous viscosity distribution problem. Instead of solving the difficult inhomogeneous viscosity problem, the effective viscosity method adjusts the real viscosity to match the molecular dynamic simulation result. Moseler and Landman [
11] and Eggers [
12] have discussed nano jet problems.
Although the MDS method has been used to model some nanoscale flow problems, as mentioned above, there is a crucial problem associated with this approach. In the MDS method, the flow velocity of the molecules caused by the applied external force is mixed with the thermal velocity. If the flow velocity is much smaller than the thermal velocity, which is usually more than 100 m·s-1, it is difficult to extract the flow velocity from the much bigger thermal velocity. As most nanoscale flow problems relevant to real applications deal with low speed flows, the direct application of MDS method is not workable. Until now, in all studies the minimum flow velocity used was several meters per second.
Certainly, MDS is correct for nanoscale flow. The problem is the method used to calculate the flow velocity is not suitable. Thus, how to extract the flow velocity is an important part in the MDS of nanoscale flow. The traditional way to extract the flow velocity is using the idea of time average because the accumulation of the thermal velocity will approach to zero while the time period is large, but this method is not always appropriate, especially when the flow velocity is less than several meters per second. That is, numerically, the accumulation of the thermal velocity will never reach zero and the algorithm based on this idea is not valid for low speed problems, regardless of the elegance of the algorithm.
In this paper we propose a new algorithm to extract the velocity caused by the external forces. The idea of this algorithm is as follows: in each time step, we calculate an increment of the flow velocity, and the total flow velocity is the accumulation of the increments in all time steps. This idea is reasonable because at any given time step, we can get the external force increment from the linear development of the total force function. This algorithm can be used to calculate nanoscale flow problem even the value of the flow velocity is very small. Furthermore, when using MDS method in the surface problems [
13,
14,
15,
16], fracture mechanics [
17,
18,
19], heat transfer problems, lubrication problems [
20], material science [
21] and friction problems [
22], we also need to calculate the moving velocity caused by the external force, or other external conditions, so the algorithm presented here is also suitable for these kinds of problems. To demonstrate the effectiveness of this new method, we simulated several examples of 2-D flow in slit nano-channels with different channel heights.
Principle of the new method
Let us consider an isothermal pressure-driven steady state 2-D Poiseuille flow in a straight channel. Let
x represent the direction of flow, while
h represents the channel height in the
y direction, that is the direction perpendicular to the flow. Each channel wall, i.e., the boundary perpendicular to the
y direction, is modeled in terms of four rows of particles of solid wall material [
5]. Initially, both the fluid particles and the solid wall particles are positioned in fcc lattices [
23]. In the
x direction we use the periodic boundary conditions [
24].
If
represents the total velocity vector of the fluid, it can be expressed by
In a macrosopoic problem, if there is no external force, the fluid will be in an equilibrium state, and the flow velocity v = 0, but when we simulate a nanoscale problem with the MDS method, even if there is no external force and it is an equilibrium molecular dynamics problem, the calculated flow velocity will never be zero. Certainly, at this time, the nonzero flow velocity is due to the modeling and numerical errors. We represent this part of the velocity by vT. When external forces are exerted, a real flow velocity of the fluid will exist. We represent this part of velocity by ve. Theoretically, vT should be zero, but numerically it is not zero. In fact, in MDS vT is not only nonzero, but it is quite big and usually equals several hundred meters per second, so if the real flow velocity is small, it is difficult to know the exact value of ve according to equation (1).
In MDS methods [
3,
4,
5], the flow velocity
ve can be calculated by
where
is the number of time steps. The subscript k refers to the k
th time step. Equation (2) is based on the concept that if
approaches infinity
This is the traditional method used in most MDS algorithms. During the calculation we consider a small volume with a specific point inside and
vk is the average velocity vector of all particles inside this volume at a particular moment [
24]. Many studies verifying this method are available when the scalar velocity
ve is not less than several meters per second, but when
ve is much smaller than the scalar velocity
vT, the above method does not work because, numerically,
vT =
0 is not true even when
is sufficiently big. Therefore we have to devise a new way to calculate the velocity
ve.
If , at the k-1
th time step, we know the velocity of the i
th particle
vik-1, then, at the k
th time step, the velocity of the i
th particle
vik can be expressed by
Let
represent the total force exerted on the i
th particle at the end of the k-1
th time step;
and
represent the force corresponding the equilibrium MDS problem and the force caused by the external loads, respectively. If there is no external load then
, but
is still nonzero. We have
. In equation (4) the increment of velocity
depends on the force
. Here
is the velocity increment caused by
at the k
th time step;
is the velocity increment caused by
at the k
th time step. So the flow velocity of the i
th particle at the k
th time step
can be calculated by
and we have the flow velocity
where the initial value of the flow velocity
and
is the mass of the i
th particle.
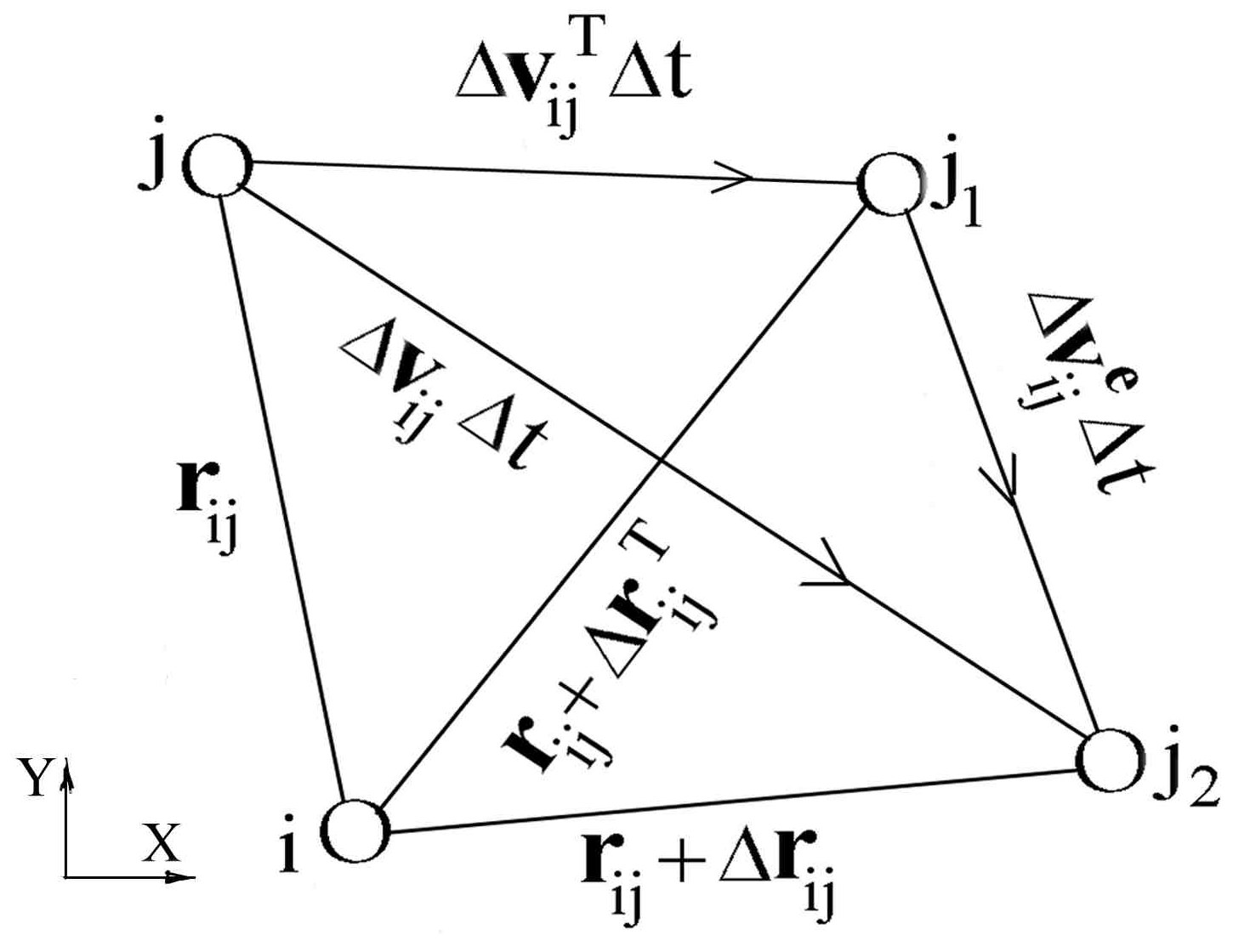
Figure 1 illustrates the positions of particles i and j at moment t and t +
, corresponding to the k-1
th and the k
th time steps, respectively. The vector distance between these two particles at moment t is
. The vector velocity difference between these two particles is
. Because only the relative positions is involved, without lose of generality, we can assume that the position of particle i is not changed. At moment t +
, because of the velocity difference
, the particle j moves from point j to point j
2. The distance between these two particles is
, where
. The distance change is
, where
;
;
and
are the velocity increments caused by the heat movement and the external forces, respectively.
From
Figure 1 we see that
. It means the distance between particles i and j is influenced by both
and
. Obviously, the distances between particles i and j are different for
and
. Also, the interaction forces are different for
and
because they are functions of
. At moment t +
, the interaction force is
. The form of
depends on the potential function. Thus, we think the interaction force as consisting of two parts. The first part corresponds to
, that is
, we represent it by
. The second part is the additional force increment because
, that is
, we represent it by
. If there is no external force, we have
and then
. So
is caused by external force. Now
consists of two parts,
, where
represents the interaction force due to the external load caused additional distance change between different particles;
represents the external load exerted directly on particle i, usually
.
depends on the form of the external load. If the potential function between the i
th particle and the j
th particle is
we have the following interaction force function
The interaction force increment between t and t+Δ t is
where
and
are the change of the scalar and vector distance
and
caused by the external conditions, respectively;
and
are the change of the scalar and vector distance
and
without external loads, respectively. From (8) we know that the increment of the interaction force between the i
th particle and the j
th particle caused by the external conditions is
Thus, at the k
th time step, the total interaction force of the i
th particle, caused by the external conditions, can be expressed by
and
are the change of the scalar distance
and the vector distance
at the k-1
th time step caused by the external conditions.
and
can be calculated according to the positions of particle i and j. At the beginning of simulation, fluid particles are allowed to move without applying the external force until a thermodynamic equilibrium state is reached. At this stage, it is an equilibrium problem. Usually, this process needs thousands of time steps or more. Then the external forces are applied and the non-equilibrium simulation starts.
According to the geometrical relation in
Figure 1 we have the following scalar distance expressions:
and
Subtracting (12) from (11) and considering
, after some mathematical manipulations, we obtain:
On the left hand side of (13) both
and
are scalar lengths. Usually
is small and both
and
are much smaller than
. We should notice here the smaller
and
are ensured by the size of
, so we do not need to assume the flow velocity is small. Considering that all the variables in (10) correspond to the k-1
th time step, we add a subscript k-1 to represent the value at this time step and then equation (13) can be simplified to
The procedure of the algorithm is: at the kth time step, for any particle i, we calculate by formulae (14) and = , then the force exerted on this particle at this moment and by (10). Finally, the flow velocity increment and the flow velocity can be calculated by (5) and (6), respectively. When using (14) to calculate the term is the velocity increment corresponding to the k-1th time step and it is already known.
The considered Poiseuille flow is a steady state problem. The system temperature should be fixed throughout the flow process. To avoid increases of the system temperature during the simulation due to external forces or other unphysical effects, a constant temperature constraint is added. If the external forces are included in the system, it becomes a non-equilibrium molecular dynamics problem. Reference [
25] is a good review regarding nonequilibrium MDS in flow problems. In this case the movement equation of particle i is
This is so called Gaussian thermostat method for nonequilibrium flow problems [
25,
26]. For equilibrium flow problems, both
and
are zero vectors in (15). Because the flow velocity should not affect the temperature of the system, in the last term of (15), we deduct it from the total velocity. Here
is the derivative vector of the velocity of the i
th particle with respect to the time variable.
is the external force vector
.
is the total interaction force exerted on the i
th particle. It is composed of two parts,
.
is the interaction force without external loads.
is the additional interaction force caused by the external force. We do not need to calculate
separately. This means that during the simulation, we do not need to use the sum of
and
to get
. We can calculate
according to
and the position of particles directly.
is a thermostat multiplier to keep the kinetic temperature constant in the system. It can be obtained from the constant temperature condition [
25,
26]. This is one of the usually used methods in thermostat molecular dynamics. When calculate the system temperature, for each particle, the flow velocity should be subtracted from the total velocity.
Simulations of 2-D Poiseuille flow
In this Poiseuille flow we assume that the external force exerted on fluid particle i is , that is . Here gi is the equivalent constant gravity acceleration vector. There are N particles within a length L along the flow direction and a height h of the flow channel. The initial velocity is given by the original temperature. In these simulations the fluid material is liquid argon and the Lennard-Jones potential is used. The cutoff radius is taken as rc = 2.5σ. The interaction between the liquid and the solid wall is considered by the interaction strength parameter of the wall particles to the liquid particles. As mentioned before, in our simulations, the solid wall particles are fixed. Certainly this fixed boundary particle assumption will influence the accuracy of the flow velocity a little but it is not affect the examination of the effectiveness of our new velocity extraction method. During the simulation we fix the positions of these four rows of particles on each side.
The values of the parameters used in the calculations are: the size of particles σ
f = σ
w = 3.4x10
-10 m; the mass of the particles m
f = m
w = 6.69x10
-26 kg; the temperature T = 84K; the interaction strength parameter between argon molecules is ε
f = 1.657x10
6 kg·m
-1·s
-1. In the above, the subscript f represents fluid and the subscript w represents solid wall. In our simulations, the size of each time step is chosen as Δt = 10
-16 s. In many papers Δt = 10
-14 s is recommended, but to ensure our linearized algorithm is stable Δt = 10
-16 s is necessary. In principle, we can use different interaction strength parameters ε
w to represent different solid wall materials [
24,
27]. We used ε
w = 3ε
f in our simulations. The interaction strength parameter for the interaction between a wall particle and a fluid particle ε
wf can be evaluated [
24,
27] by ε
wf = (ε
fε
w)
½. In all the simulations the density number is 0.82, corresponding to the liquid density of argon at T=84 K.
We calculated two different cases with different channel heights. For the first case, L=13.61nm; h=2.31 nm; N=243. For the second case, L=13.61 nm; h= 4.36 nm; N=459. The velocity profiles calculated in our simulations for these two cases are plotted in
Figure 2,
Figure 3,
Figure 4 and
Figure 5.
Because in this new method the total flow velocity
ve is the linear accumulation of velocity increment of each time step we call it the LA method. The traditional method is based on the idea of time average, we call this the TA method.
Figure 2 shows the simulation of case 1. In this simulation the equivalent acceleration in the flow direction is 10
13 m·s
-2 and the simulated maximum velocity which is calculated in the
x direction by the method of this paper (the LA method) is 39.9 m·s
-1. The MDS result where the velocity is calculated by the traditional method (TA method) is also shown in the Figure. Because the velocity is big both the TA and LA methods can be used to calculate the flow velocity.
Figure 3 is another example of case 1, where the pressure difference is smaller. The equivalent acceleration in the flow direction is 10
9 m·s
-2 and the maximum velocity in the
x direction is 3.92x10
-3 m·s
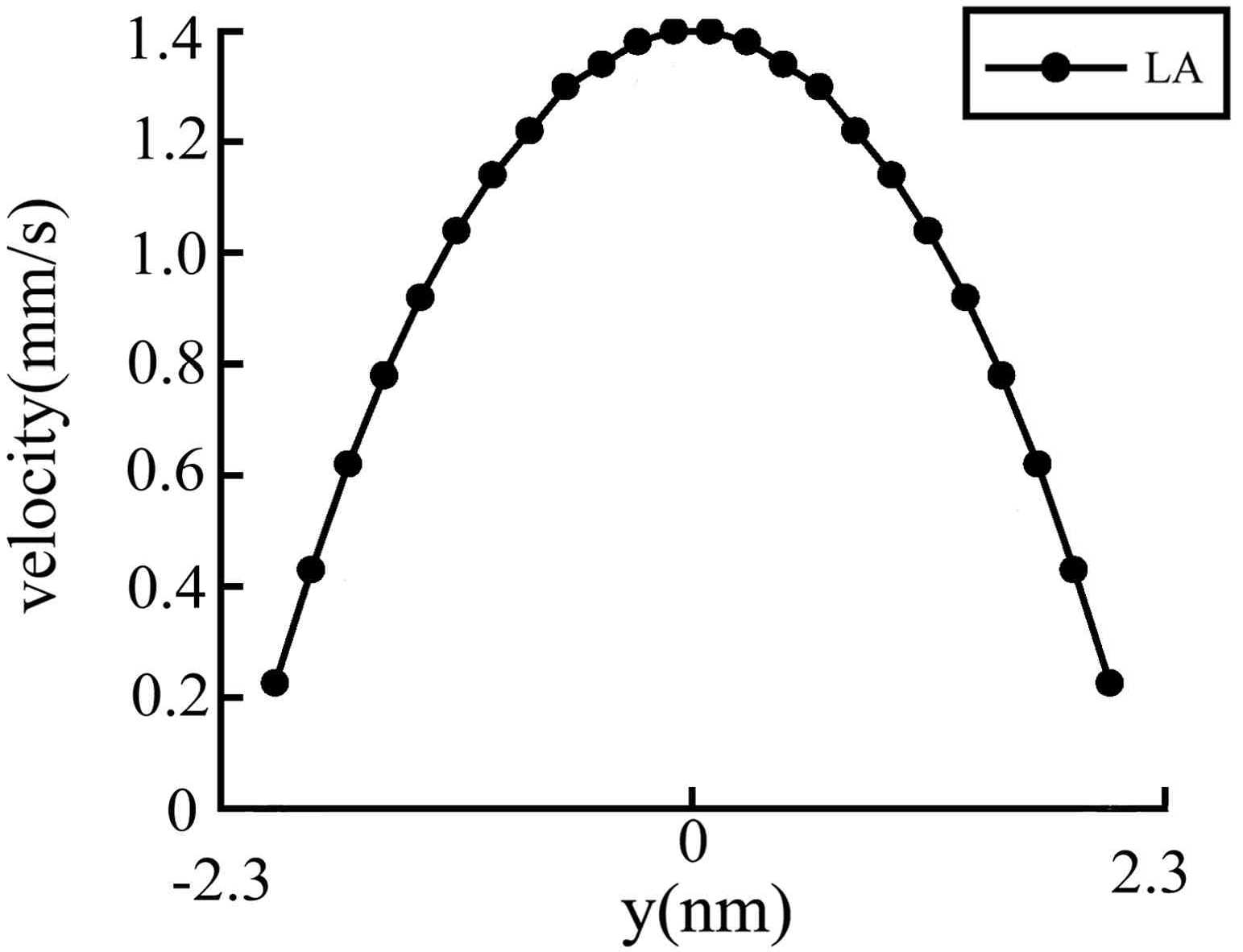
-1.Because the flow velocity is much smaller than the thermal velocity, the traditional method (TA method) is not available, but, as shown in the Figure, the LA method proposed in this paper is still effective.
Figure 4 shows the simulation of case 2. In this simulation the equivalent acceleration in the flow direction is 10
12 m·s
-2 and the maximum velocity in the
x direction is 13.92 m·s
‑1.
Figure 5 is another example of case 2, where the equivalent acceleration in the flow direction is 10
8 m·s
-2 and the maximum velocity in the
x direction is 1.37x10
-3 m·s
-1. In
Figure 3 and
Figure 5 we can only get results for the LA method because in these simulation situations or for such small flow velocities the TA method is not available. In fact, when we simulated the same problems with the TA method under the same conditions as in
Figure 3 and
Figure 5, the maximal flow velocity is always great than 2 m·s
-1. Certainly this is not the correct solution of the problems. Up to now, we have not found any algorithm which can be used to solve such a low velocity nanoscale flow problem. That is why the LA method is important for low flow velocity problems. However, we can compare the results of TA and LA methods for high flow velocity cases, as shown in
Figure 2 and
Figure 4. Because, in principle, the LA method can be used for both high and low flow velocity problems the conclusions obtained from the high flow velocity comparisons can be extended to low flow velocity problems.
These numerical examples demonstrate that the velocity extraction method proposed in this paper is a suitable approach for both low and high speed flow problems. When the flow velocity is big the result of LA method is the same as the result of TA method. When the flow velocity is small TA method is not available we have to use LA method to extract ve.
Convergence and Efficiency analysis
In this new algorithm, we only used the linear terms of the development of the force function with respect to
to approximate the force increment caused by the external conditions. What is the influence of the truncate errors of this approximation? Is it convergent and what are the conditions of convergence? These are the questions which should be answered for a reliable algorithm. We do a series of simulations with different size of time step from Δt = 10
-14 s to Δt = 10
-18 s. We find that when Δt = 10
-14 s the simulation of our new velocity extraction method is not good. This means for the linear approximation the size of time step should be smaller. If the time step is big the small
assumption will be broken. When Δt = 10
-18 s the result is almost the same with the result of Δt = 10
-17 s. So we have reason to believe that when Δt = 10
-17 s the simulation is already convergent. We show the simulation results with time step size from Δt = 10
-15 s to Δt = 10
-17 s in
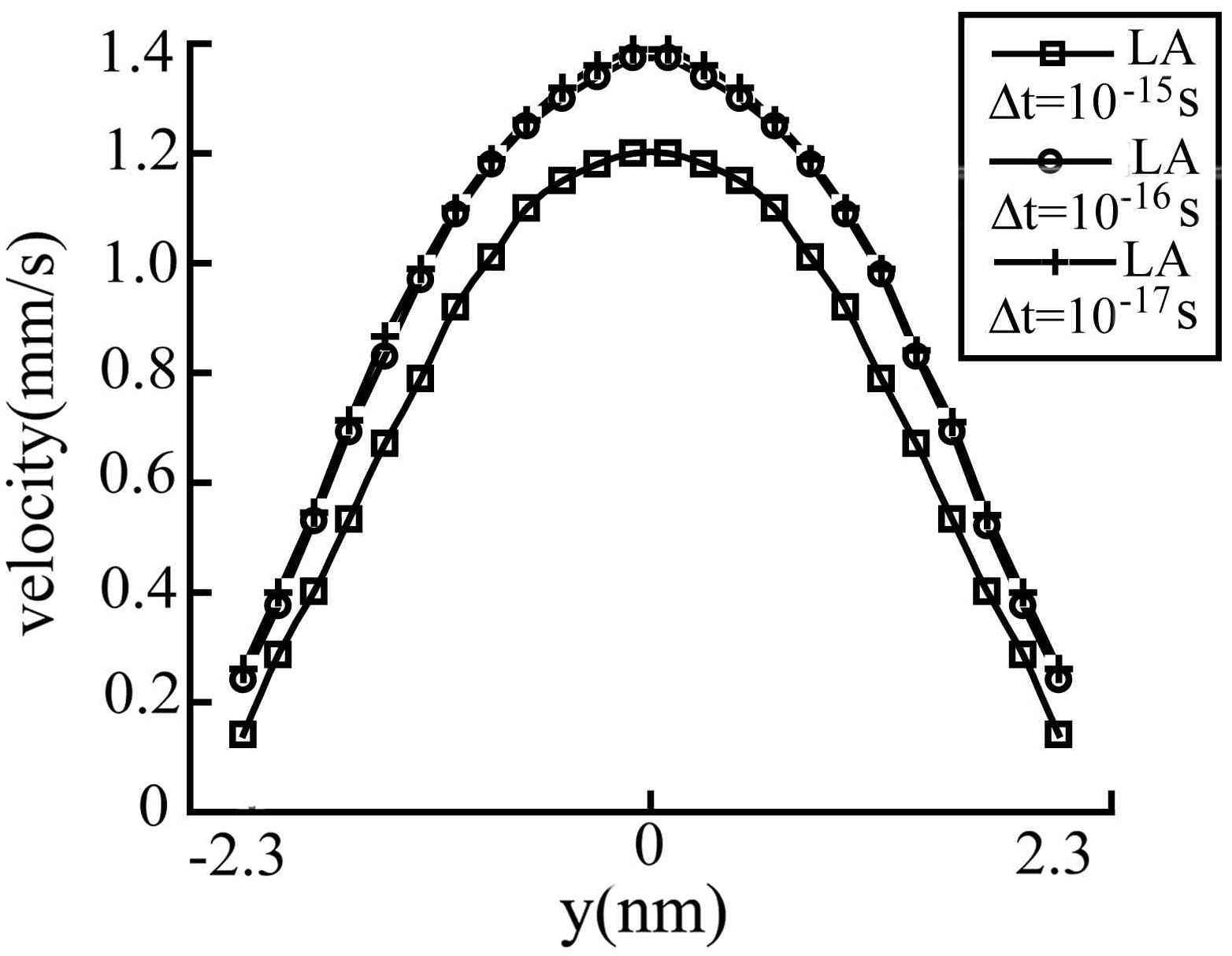
Figure 6. From this figure we see that when Δt = 10
-15 s the simulation result is far from convergence and when Δt = 10
-16 s we obtain a quite satisfactory result. If we let Δt = 10
-17 s the result is only improved a little, so for practical applications, the recommended time step size is Δt = 10
-16 s.
(LA Method). Low flow velocity simulations of case 2. The vertical coordinate is the flow velocity and the horizontal coordinate is the height of the channel.
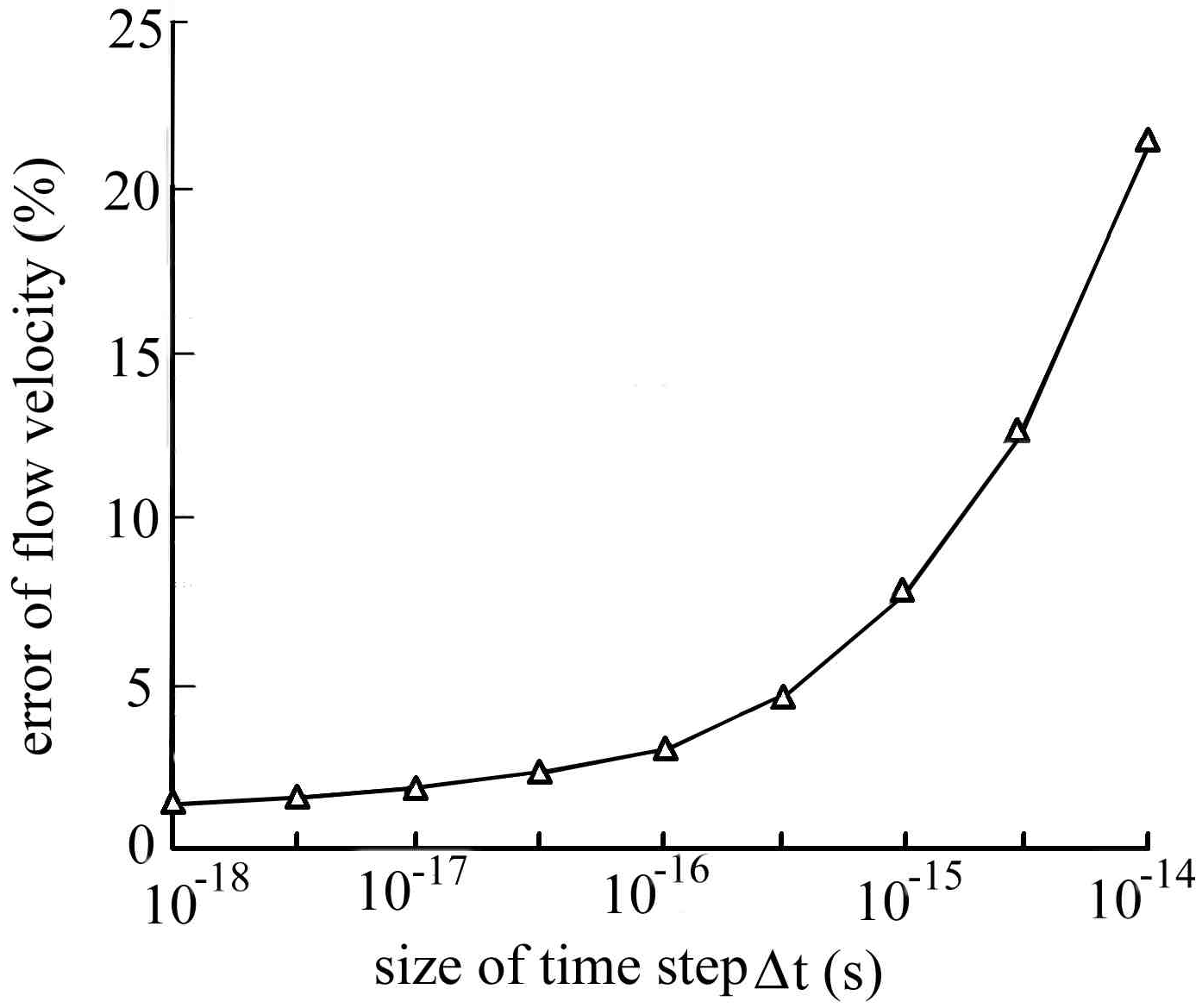
Figure 7 is the analysis of the error of the maximal flow velocity when the size of the time step is changed (LA Method). The simulation conditions are the same as the simulations in
Figure 4. The vertical coordinate is the error of the maximal flow velocity
100% and the horizontal coordinate is size of the time step
(s), where v
max LA is the maximal velocity of this paper and v
max TA is the maximal velocity of TA method.
Although the purpose of this new method is to extract the low flow velocity caused by the external conditions, which the conventional MDS method can not do, the efficiency of an algorithm is always an important part to be considered. In our new method we use Δt = 10
-16 s. For the similar problems, in conventional MDS methods, Δt = 10
-14 s is usually used. Because in this new method we do not need extra iterations to calculate the flow velocity, even 100 times smaller time step size is used, the total number of time steps is still less than that of the conventional MDS method. The simulation software was executed on a Pentium 2.8GHz PC. We compared the CPU time and the number of time steps as follows. In
Figure 2, we used 89800 time steps (51 minutes CPU time) for LA method and 3.2x10
5 time steps (108 minutes CPU time) for the TA method; in
Figure 4, we used 288400 time steps (565 minutes CPU time) for the LA method and 7.8 x10
5 time steps (1022 minutes CPU time) for the TA method. The efficiency of the new method is evident.
 is the result of this paper (LA ).
is the result of this paper (LA ).  is the result of the traditional (TA) method.
is the result of the traditional (TA) method.
 is the result of this paper (LA ).
is the result of this paper (LA ).  is the result of the traditional (TA) method.
is the result of the traditional (TA) method. 
 is the result of this paper (LA ).
is the result of this paper (LA ).
 is the result of this paper (LA ).
is the result of this paper (LA ). 
 is the result of this paper (LA ).
is the result of this paper (LA ).  is the result of the traditional (TA) method.
is the result of the traditional (TA) method.
 is the result of this paper (LA ).
is the result of this paper (LA ).  is the result of the traditional (TA) method.
is the result of the traditional (TA) method.
 is the result of this paper (LA ).
is the result of this paper (LA ).
 is the result of this paper (LA ).
is the result of this paper (LA ).