Formation Flight of Multiple UAVs via Onboard Sensor Information Sharing
Abstract
:1. Introduction
2. Sensor and UAV System
2.1. Sensors

| Component | Model Name | Manufacturer | Data Rate | Specification |
|---|---|---|---|---|
| Inertial navigation sensor | 3DM-GX3-45 | Microstrain | 50 Hz | Typ. Attitude accuracy ±0.35° Typ. Velocity accuracy ± 0.1 m/s Typ. Position accuracy ± 2.5 m RMS |
| AOA, AOS sensor | 3MA-A10-125-B | US Digital | 50 Hz | 12-bit resolution, 0.08° accuracy |
| Airspeed sensor | MPX7002DP | Freescale | 50 Hz | Typ. Pressure accuracy ± 1.6 Pa |
| RF telemetry | XBP09-DMUIT-156 | Digi | 10 Hz | 3 Km LOS range, 900 MHz |
| FCC | ARM FCC-M3 | Self-developed | 400 Hz | ARM Cortex-M3, 72 MHz Clock, 6 Ch PWM In & Out |
2.2. UAV Airframe

2.3. UAV System Identification

3. Onboard Sensor Information Sharing via Wireless Communication
| Wi-Fi | Bluetooth | ZigBee | |
|---|---|---|---|
| Range | 50–100 m | 10–100 m | 100 m–1 km |
| Network Topology | Point to Hub Ad-hoc | Ad-hoc | Ad-hoc, peer to peer, star, mesh |
| Frequency | 2.4 GHz and 5 GHz | 2.4 GHz | 868 MHz, 900 MHz, 2.4 GHz |
| Complexity | High | High | Low |
| Power Consumption | High | Middle | Very low |
| Security | WEP | 64-bit or 128-bit encryption | 128 AES or AL |
| Applications | -Wireless LAN | -Wireless device connection | -Industrial monitoring-Sensor network |
| Data | Header | Status | Latitude | Longitude | Height | GPS Time | Roll | Pitch | Yaw | P |
|---|---|---|---|---|---|---|---|---|---|---|
| Byte | 1–2 | 3–6 | 7–10 | 11–14 | 15–18 | 19–22 | 23–26 | 27–30 | 31–34 | 35–38 |
| Q | R | Vel N | Vel E | Vel D | Acc X | Acc Y | Acc Z | Air Height | Air speed | Gamma Cmd |
| 39–42 | 43–46 | 47–50 | 51–54 | 55–58 | 59–62 | 63–66 | 67–70 | 71–74 | 75–78 | 79–82 |
| Roll Cmd | Battery | Elevator | Rudder | Throttle | Aileron | Alpha | Beta | Stage | Reserved | Putter |
| 83–86 | 87–90 | 91–94 | 95–98 | 99–102 | 103–106 | 107–110 | 111–114 | 115–118 | 119–122 | 12–124 |

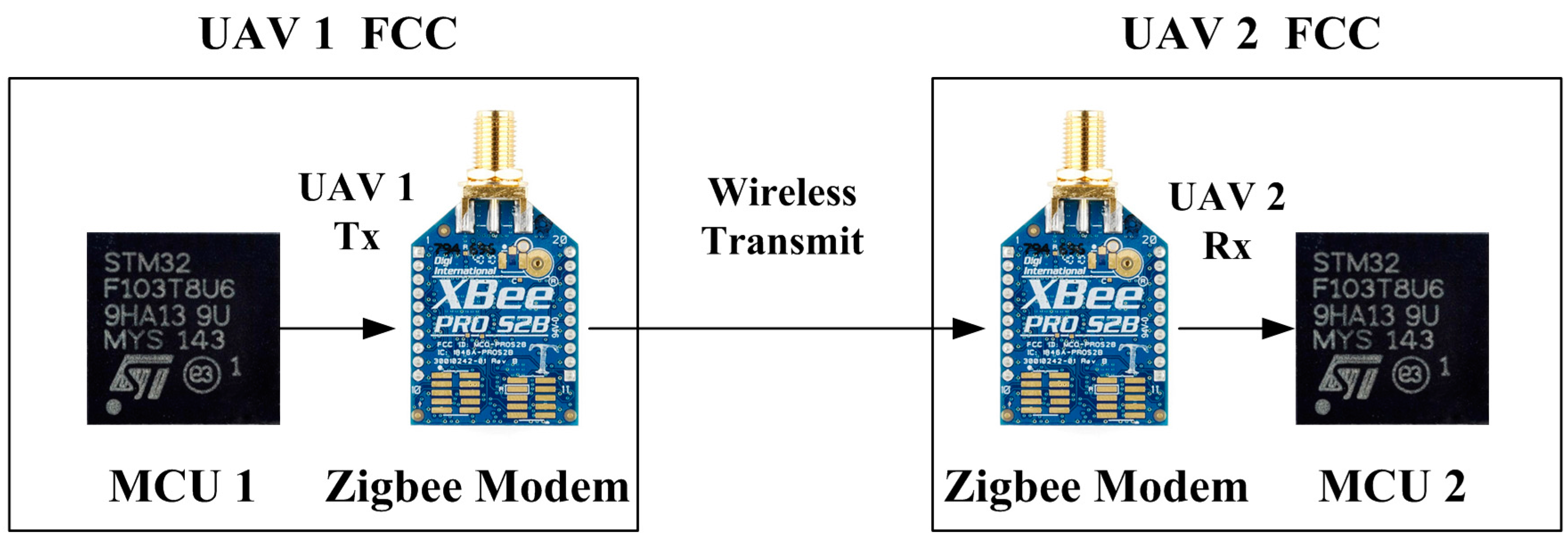
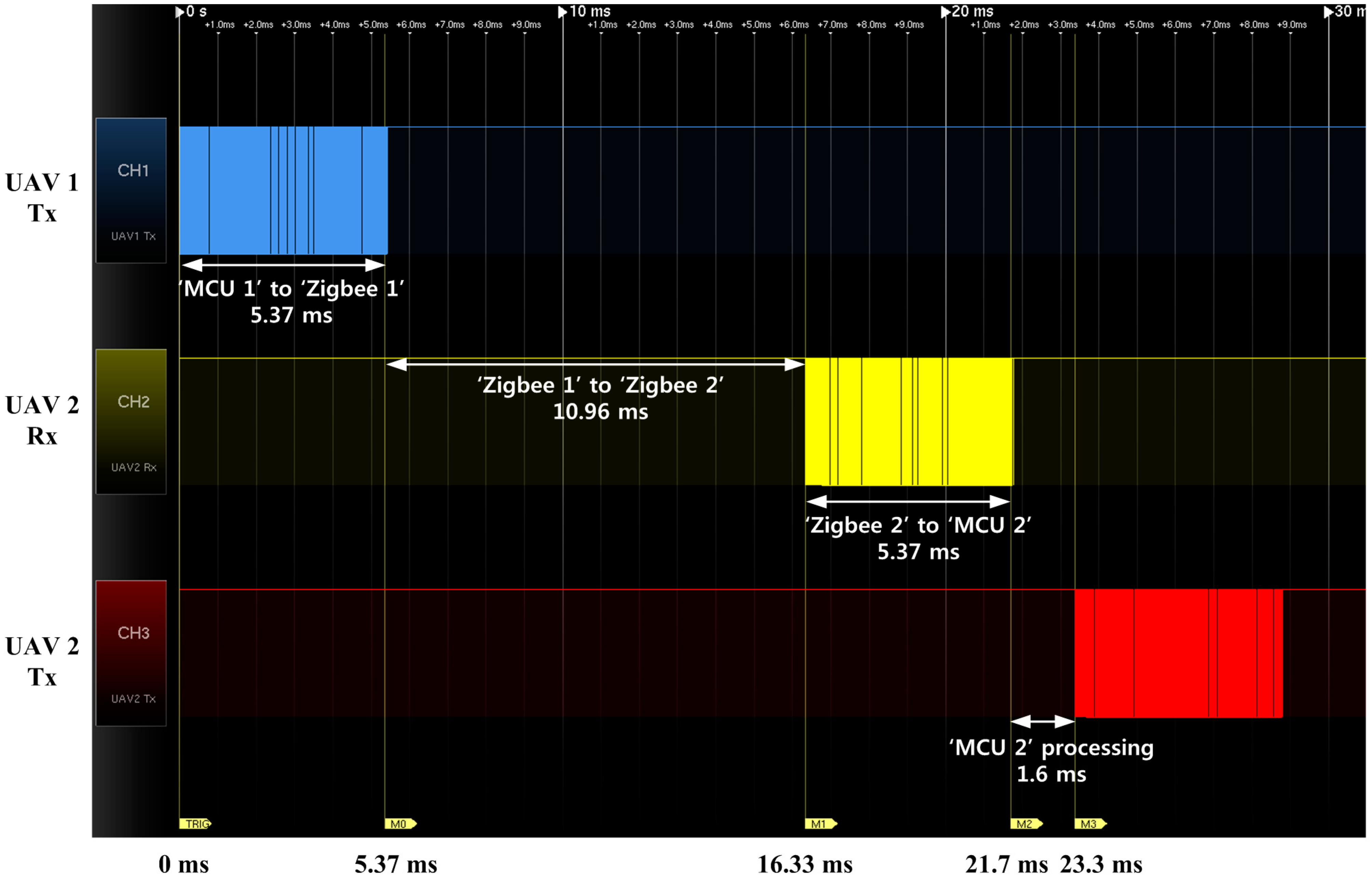

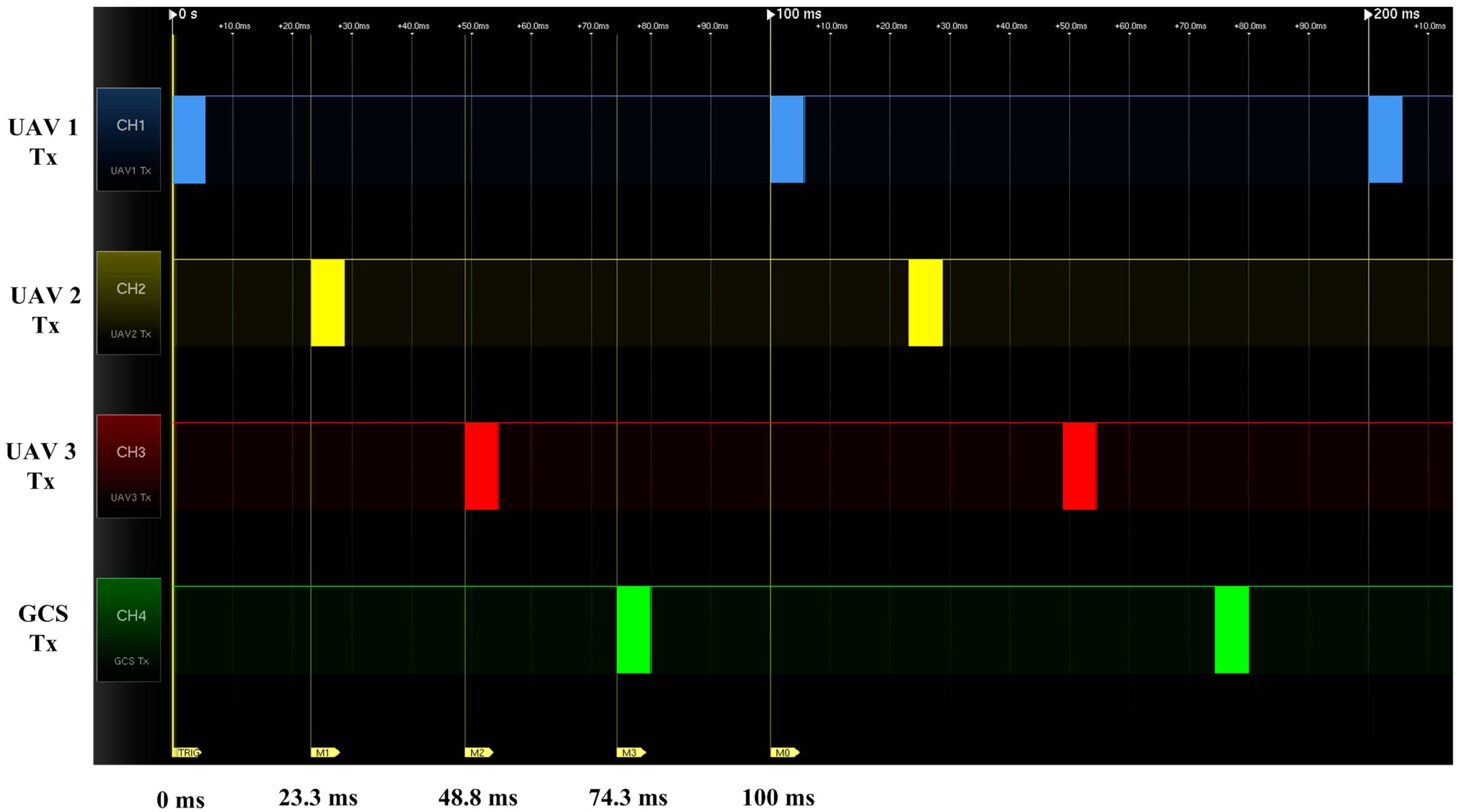
4. Guidance Algorithms for Formation Flight
4.1. Circular Formation Flight Guidance
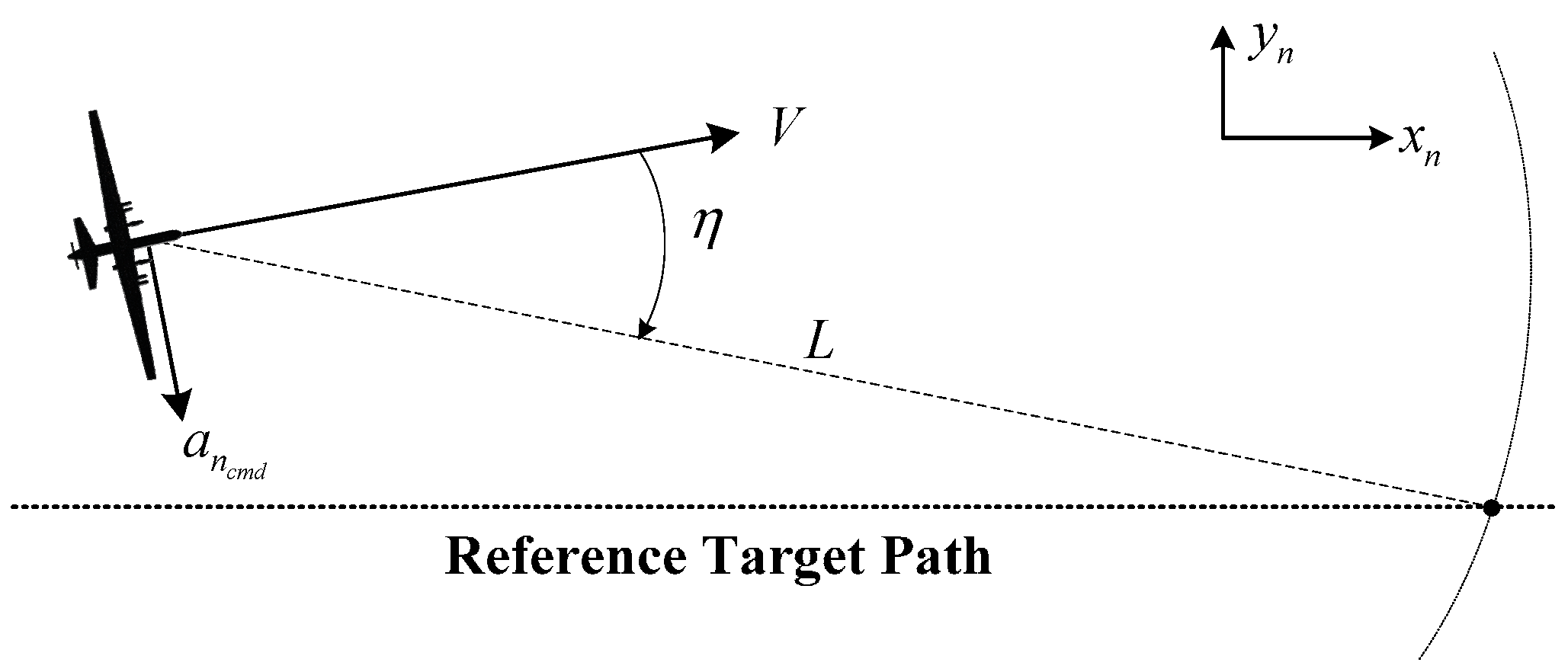
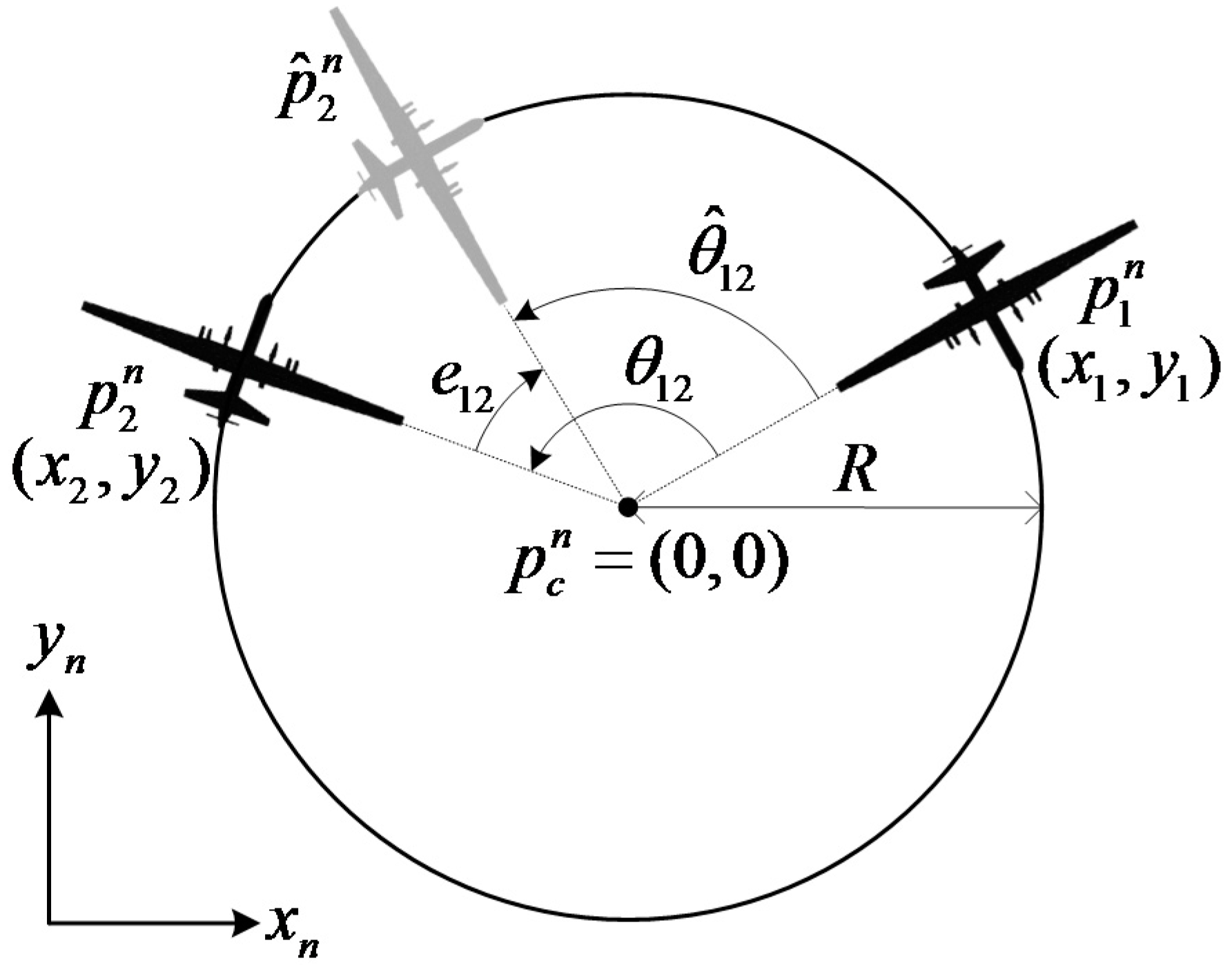
4.2. Close Formation Flight Guidance
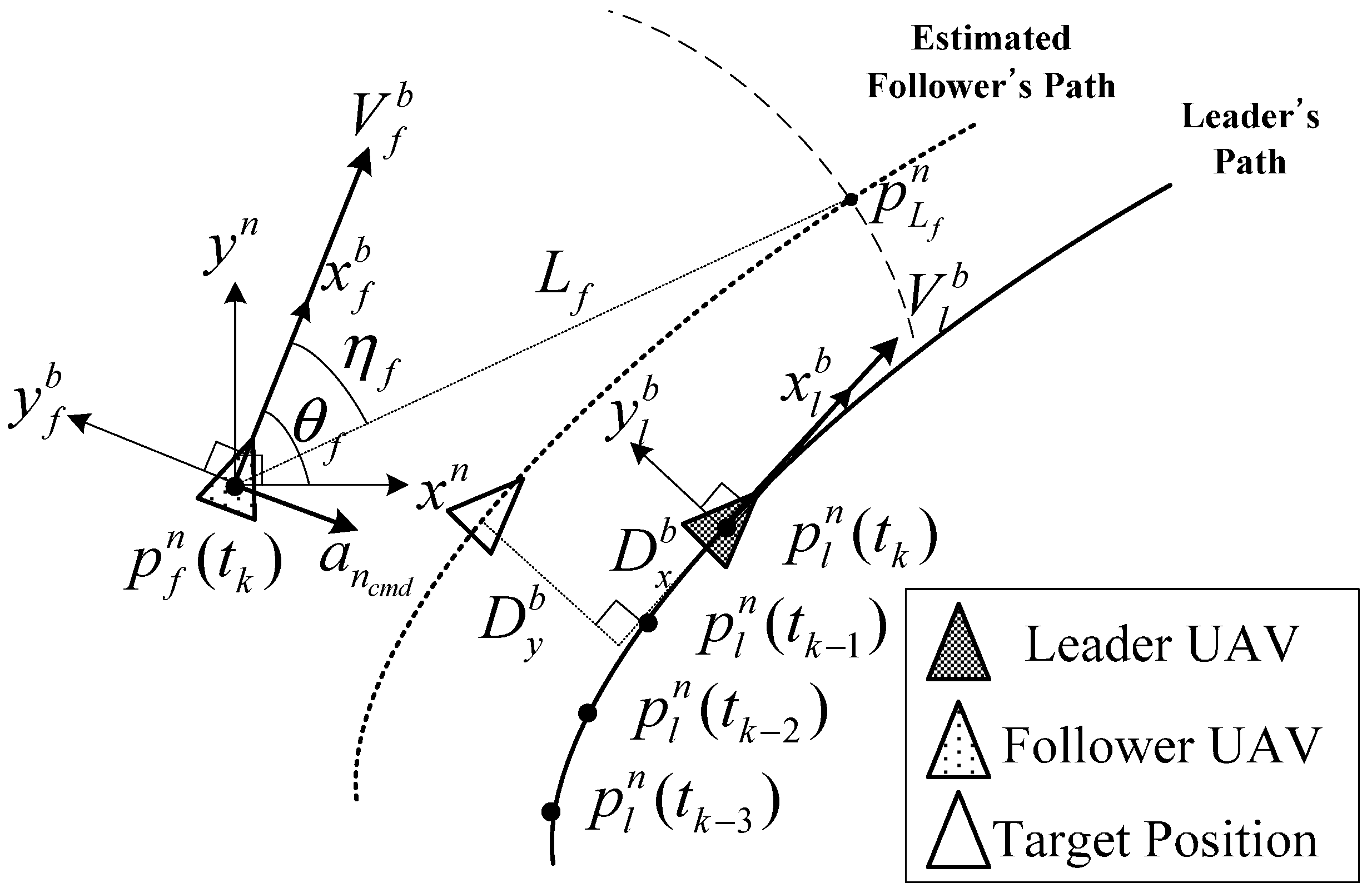
5. Simulation and Experimental Results
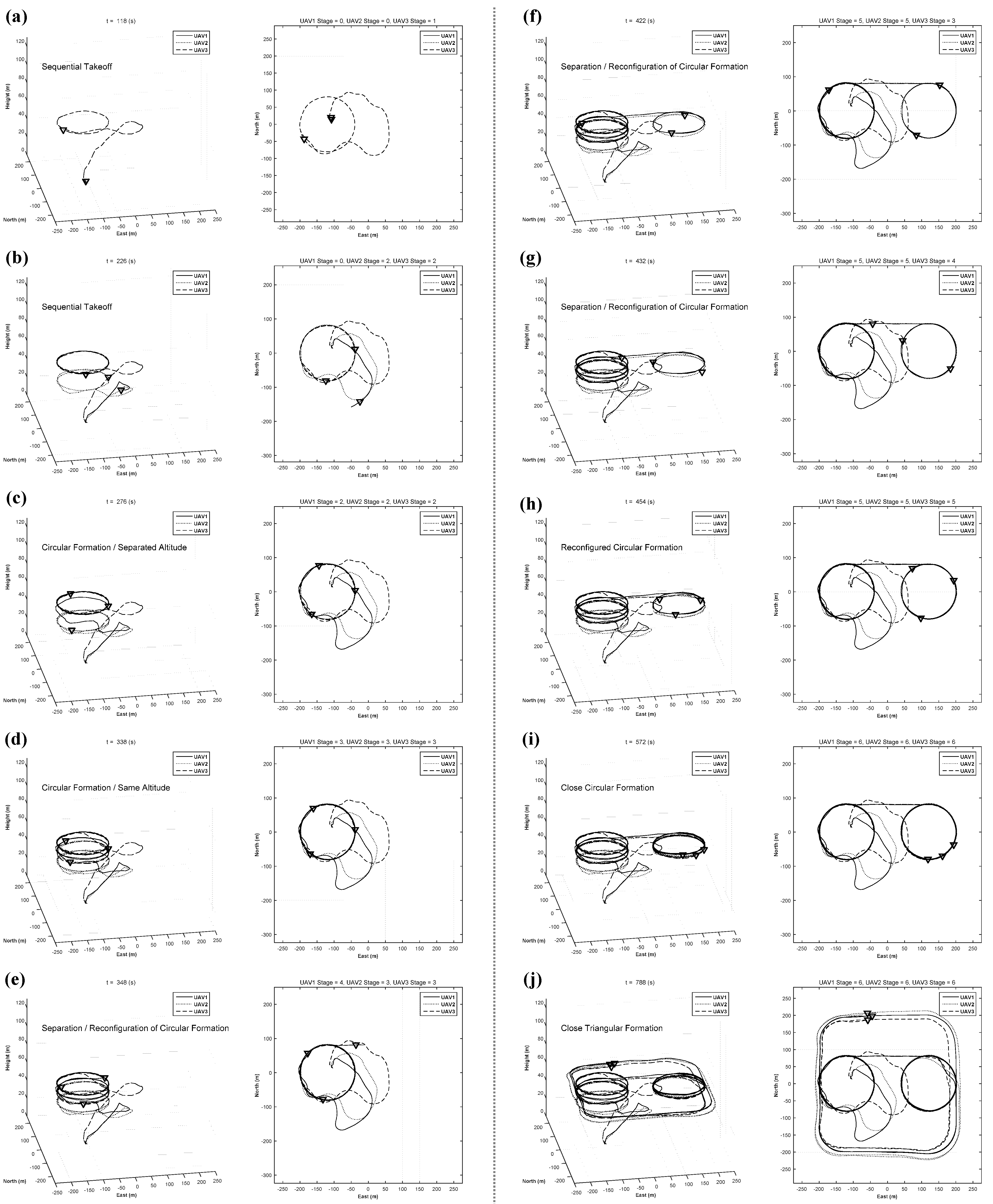
5.1. Procedure for Autonomous Formation Flight
| Scenario | Maneuver | Mission | Stage | Longitudinal Guidance | Lateral Guidance |
|---|---|---|---|---|---|
| - | Sequential takeoff | - | - | - | - |
| 1 | Circular formation/Separated altitude | 1 | 1,2 | phase separation/ | Circular path following approximately 1st target |
| 2 | Circular formation/ Same altitude | 1 | 3 | phase separation/ | Circular path following approximately 1st target |
| 3 | Separation and Reconfiguration ofCircular formation | 1 | 4,5 | phase separation/ | Transition from 1st target to 2nd target |
| 4 | Close circular formation | 1 | 6 | phase separation/ | Circular path following approximately 2nd target |
| 5 | Close triangular formation | 2 | - | −10 m rear position of leader UAV/ | ±10 m left/right position of leader UAV |
| - | Sequential landing | - | - | Longitudinal guidance | - |
5.1.1. Circular Formation Flight with Separated Altitude

5.1.2. Circular Formation Flight at the Same Altitude
5.1.3. Separation and Reconfiguration Formation Flight of the Circular Formation
5.1.4. Close Circular Formation Flight
5.1.5. Close Triangular Formation Flight
5.2. Simulation Results

5.3. Experimental Results
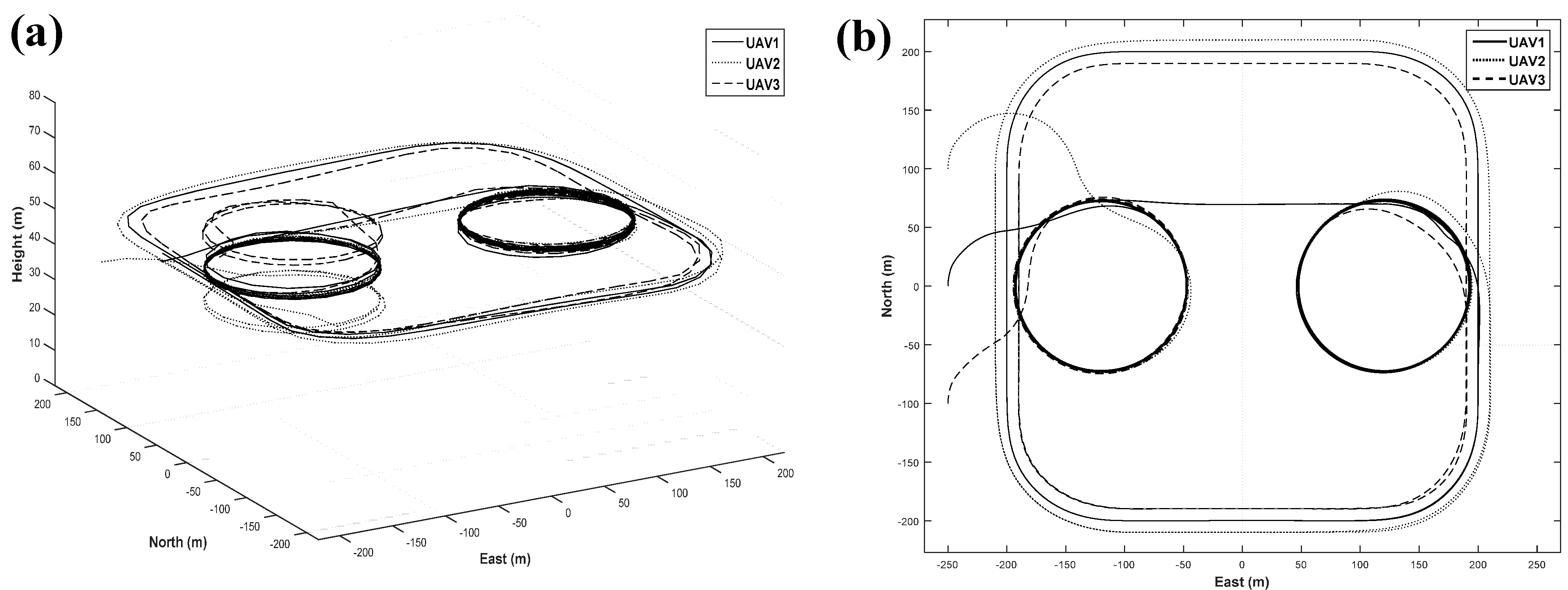
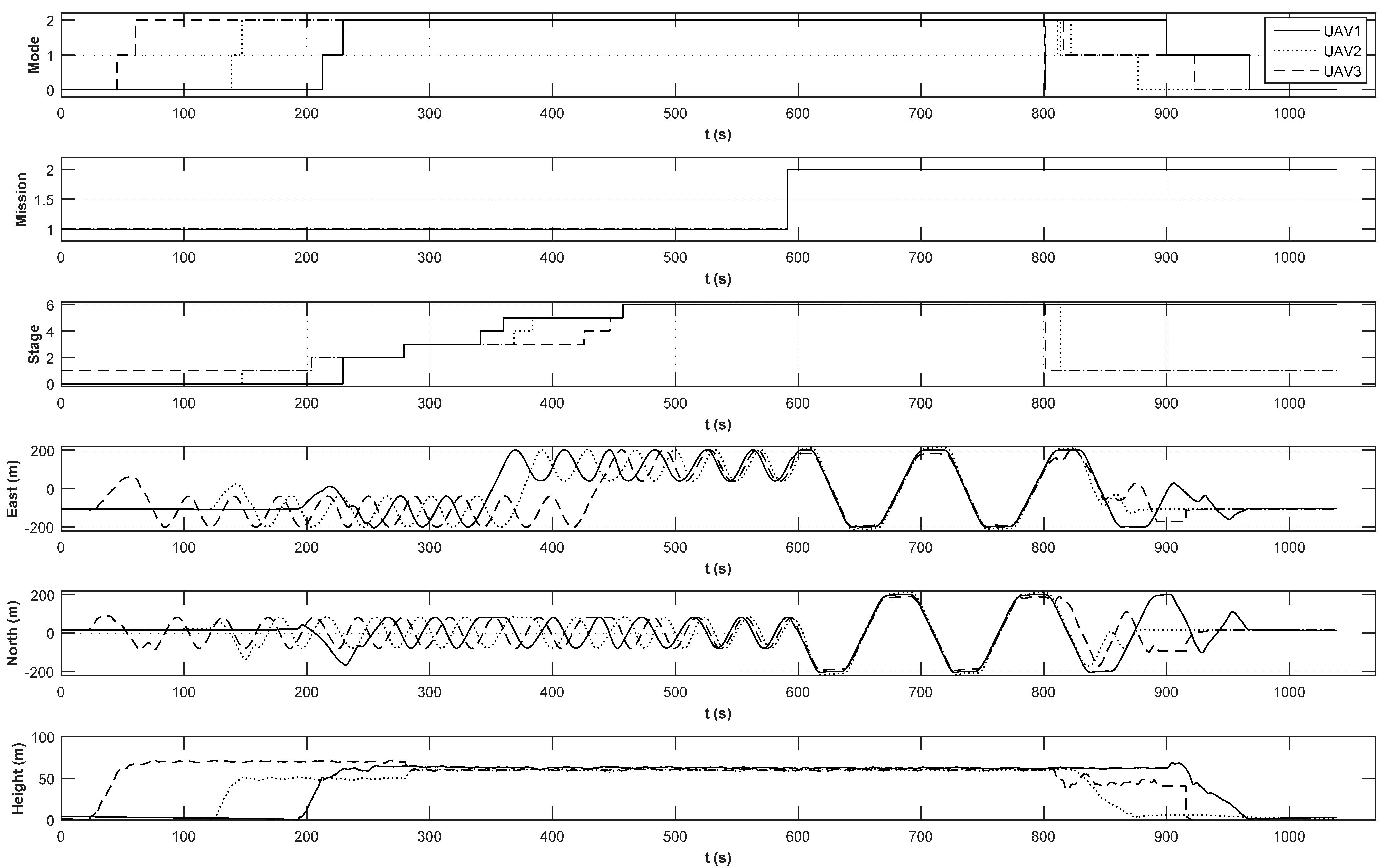
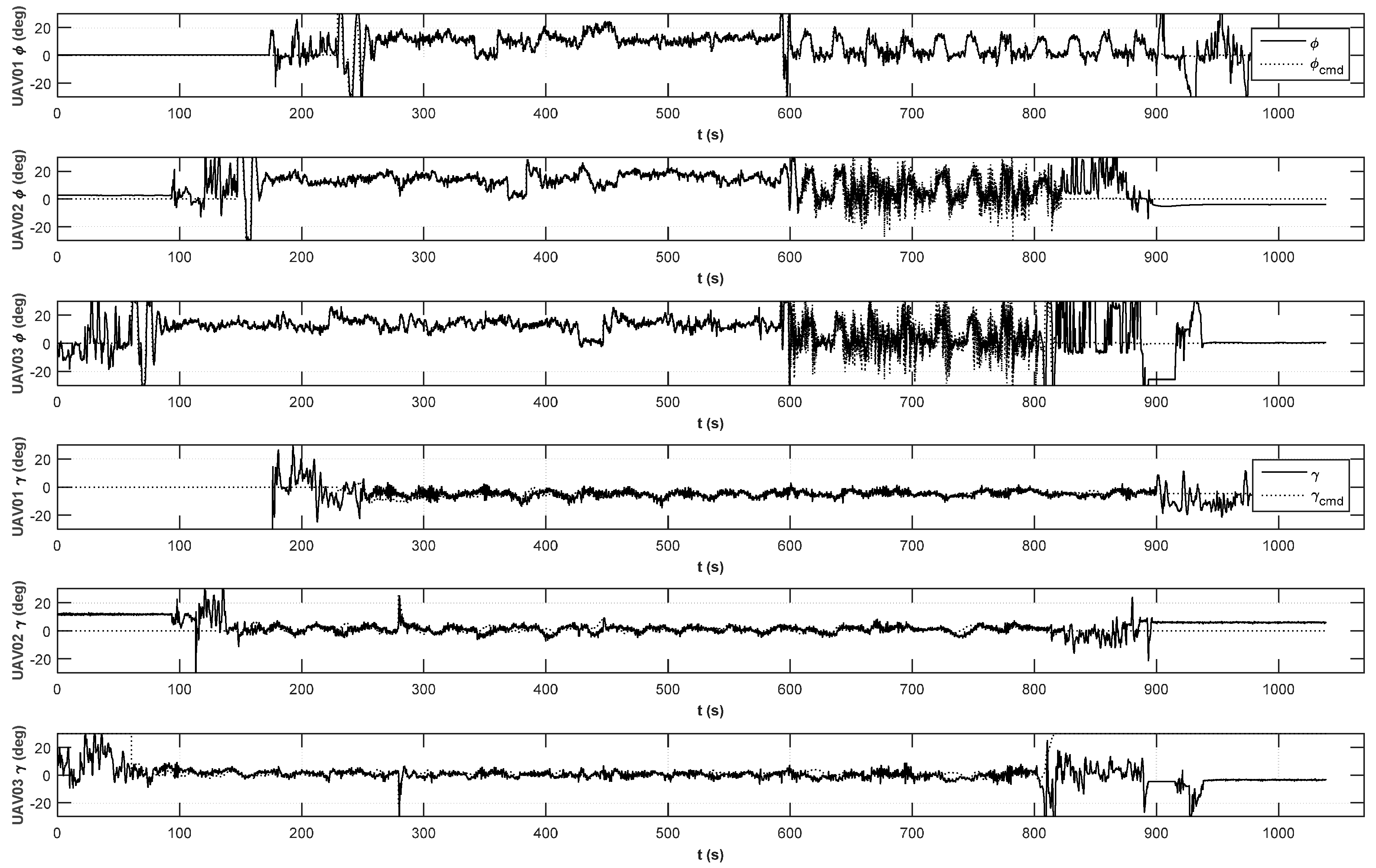


6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Giulietti, F.; Pollini, L.; Innocenti, M. Formation Flight Control: A Behavioral Approach. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Montreal, QC, Canada, 6–9 August 2001.
- Price, C.R. The Virtual UAV Leader. In Proceedings of the AIAA Infotech, Rohnert Park, CA, USA, 7–10 May 2007.
- Li, N.H.M.; Liu, H.H.T. Multiple UAVs Formation Flight Experiments Using Virtual Structure and Motion Synchronization. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Chicago, IL, USA, 10–13 August 2009.
- Teo, R.; Jang, J.S.; Tomlin, C.J. Automated Multiple UAV Flight—The Stanford Dragon Fly UAV Program. In Proceedings of the 43rd IEEE Conference on Decision and Control, Atlantis, Paradise Island, Bahamas, 14–17 December 2004.
- Verma, A.; Wu, C.; Castelli, V. UAV Formation Command and Control Management. In Proceedings of the 2nd AIAA Unmanned Unlimited System, Technologies, and Operations, San Diego, CA, USA, 15–18 September 2003.
- Schmitt, L.; Fichter, W. Collision-Avoidance Framework for Small Fixed-Wing Unmanned Aerial Vehicles. J. Guid. Control. Dyn. 2014, 37, 1323–1328. [Google Scholar] [CrossRef]
- Beard, R.W.; McLain, T.W.; Nelson, D.B.; Kingston, D.; Johanson, D. Decentralized Cooperative Aerial Surveillance Using Fixed-Wing Miniature UAVs. IEEE Proc. 2006, 94, 1306–1324. [Google Scholar] [CrossRef]
- Mahboubi, Z.; Kolter, Z.; Wang, T.; Bower, G. Camera Based Localization for Autonomous UAV Formation Flight. In Proceedings of the AIAA Infotech, St. Louis, MO, USA, 29–31 March 2011.
- Lee, H.B.; Moon, S.W.; Kim, W.J.; Kim, H.J. Cooperative Surveillance and Boundary Tracking with Multiple Quadrotor UAVs. J. Inst. Control. Robot. Syst. 2013, 19, 423–428. [Google Scholar] [CrossRef]
- Geoffrey, B.; Ted, M.; Michael, L.; Mark, M.; Joseph, B. “Mini UAVs” for Atmospheric Measurements. In Proceedings of the AIAA Infotech, Rohnert Park, CA, USA, 7–10 May 2007; pp. 461–470.
- Kim, S.; Oh, H.; Tsourdos, A. Nonlinear Model Predictive Coordinated Standoff Tracking of Moving Ground Vehicle. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Portland, OR, USA, 8–11 August 2011.
- Yamasaki, T.; Balakrishnan, S.N.; Takano, H.; Yamaguchi, I. Coordinated Standoff Flights for Multiple UAVs via Second-Order Sliding Modes. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Kissimmee, FL, USA, 5–9 January 2015.
- Venkataramanan, S.; Dogan, A. A Multi-UAV Simulation for Formation Reconfiguration. In Proceedings of the AIAA Modeling and Simulation Technologies Conference, Providence, RI, USA, 16–19 August 2004.
- Gu, Y.; Seanor, B.; Campa, G.; Napolitano, M.R.; Rowe, L.; Gururajan, S.; Wan, S. Design and Flight Testing Evaluation of Formation Control Laws. IEEE Trans. Control. Syst. Technol. 2006, 14, 1105–1112. [Google Scholar] [CrossRef]
- Bayraktar, S.; Fainekos, G.E.; Pappas, G.J. Experimental Cooperative Control of Fixed-Wing Unmanned Aerial Vehicles. In Proceedings of the Conference on Decision and Control, Los Angeles, CA, USA, 15–17 December 2004.
- Maza, I.; Kondak, K.; Bernard, M.; Ollero, A. Multi-UAV Cooperation and Control for Load Transportation and Deployment. J. Intell. Robot. Syst. 2010, 57, 417–449. [Google Scholar] [CrossRef]
- Park, C.; Kim, H.J.; Kim, Y. Real-Time Leader-Follower UAV Formation Flight Based on Modified Nonlinear Guidance. In Proceedings of the 29th Congress of the International Council of the Aeronautical Sciences, St. Petersburg, Russia, 7–12 September 2014.
- Oh, G.; Park, C.; Kim, M.; Park, J.; Kim, Y. Small UAV System Identification in Time Domain. In Proceedings of the Spring Conference of KSAS, High One Resort, Gangwon-Do, Korea, 11–13 April 2012.
- Kim, H.J.; Kim, M.; Lim, H.; Park, C.; Yoon, S.; Lee, D.; Choi, H.; Oh, G.; Park, J.; Kim, Y. Fully Autonomous Vision-Based Net-Recovery Landing System for a Fixed-Wing UAV. IEEE/ASME Trans. Mechatron. 2013, 18, 1320–1332. [Google Scholar] [CrossRef]
- Park, S.; Deyst, J.; How, J.P. Performance and Lyapunov Stability of a Nonlinear Path-Following Guidance Method. J. Guid. Control. Dyn. 2007, 30, 1718–1728. [Google Scholar] [CrossRef]
- Kim, D.; Park, S.; Nam, S.; Suk, J. A Modified Nonlinear Guidance Logic for a Leader-Follower Formation Flight of Two UAVs. In Proceedings of the International Conference on Control, Automation Systems-SICE, Fukuoka, Japan, 18–21 August 2009.
- Lee, D.; Lee, J.; Kim, S.; Suk, J. Design of a Track Guidance Algorithm for Formation Flight of UAVs. J. Inst. Control. Robot. Syst. 2014, 20, 1217–1224. [Google Scholar] [CrossRef]
- Formation Flight of Multiple UAV. Available online: https://youtu.be/6NVlgST9agQ (accessed on 16 July 2015).
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, C.; Cho, N.; Lee, K.; Kim, Y. Formation Flight of Multiple UAVs via Onboard Sensor Information Sharing. Sensors 2015, 15, 17397-17419. https://0-doi-org.brum.beds.ac.uk/10.3390/s150717397
Park C, Cho N, Lee K, Kim Y. Formation Flight of Multiple UAVs via Onboard Sensor Information Sharing. Sensors. 2015; 15(7):17397-17419. https://0-doi-org.brum.beds.ac.uk/10.3390/s150717397
Chicago/Turabian StylePark, Chulwoo, Namhoon Cho, Kyunghyun Lee, and Youdan Kim. 2015. "Formation Flight of Multiple UAVs via Onboard Sensor Information Sharing" Sensors 15, no. 7: 17397-17419. https://0-doi-org.brum.beds.ac.uk/10.3390/s150717397





