Staring Spotlight SAR with Nonlinear Frequency Modulation Signal and Azimuth Non-Uniform Sampling for Low Sidelobe Imaging
Abstract
:1. Introduction
2. NLFM Signal and Azimuth Non-Uniform Sampling
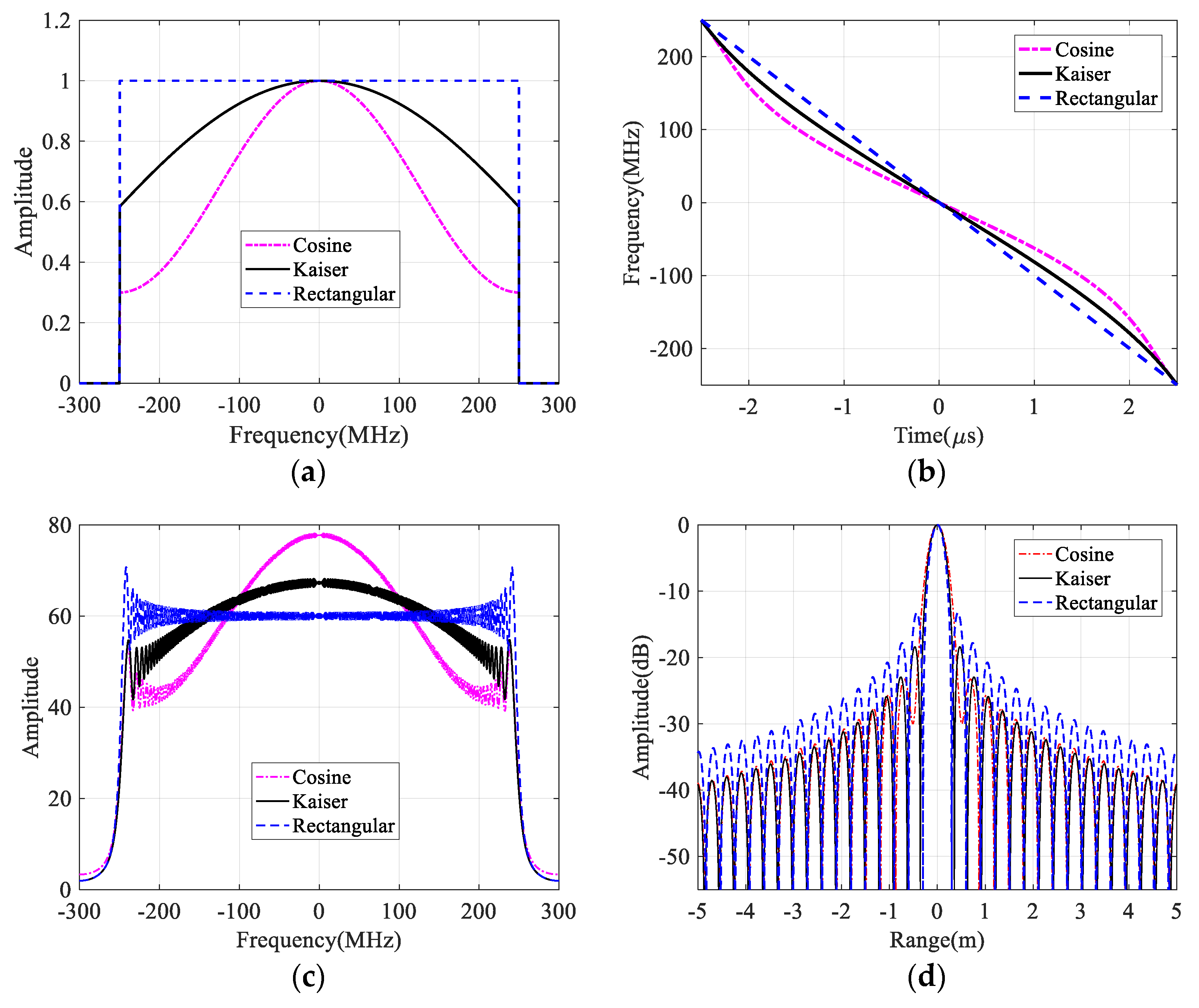
2.1. Review of NLFM Design
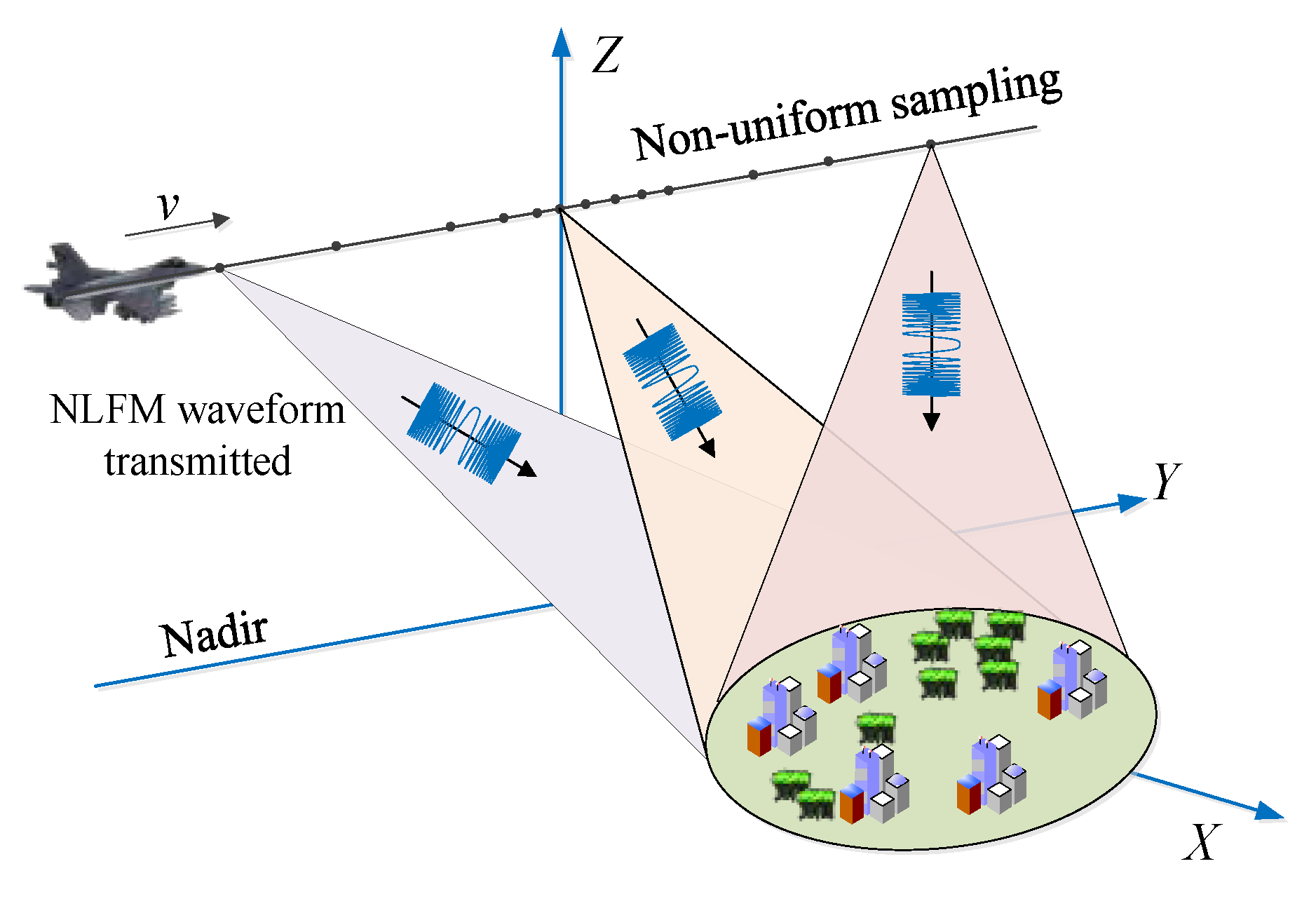
2.2. Azimuth Non-Uniform Sampling
3. High Resolution Low Sidelobe Imaging
3.1. Starring Spotlight SAR with NLFM and ANUS
3.2. SNR Loss Due to Window Weighting
3.3. Imaging Algorithms
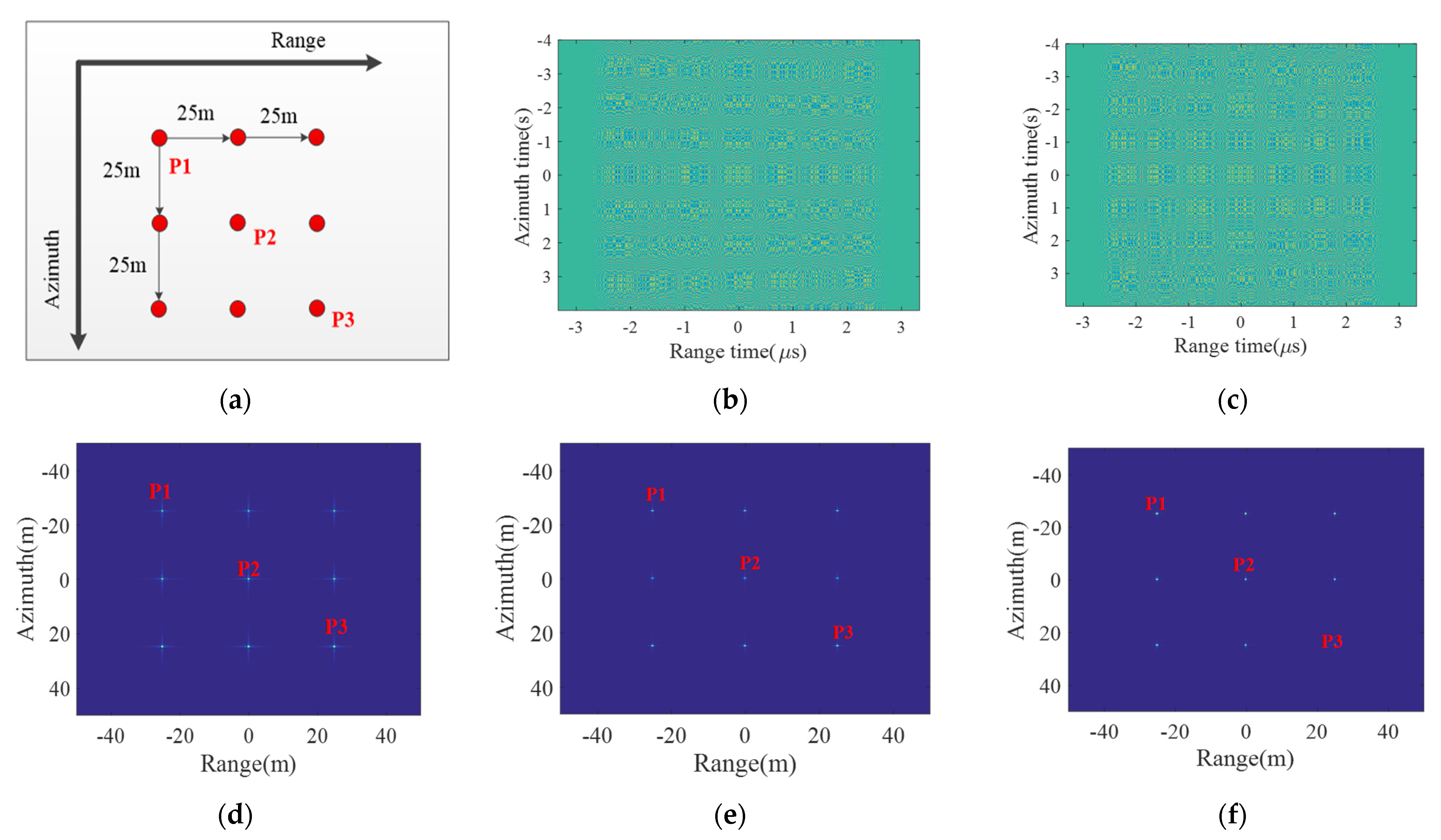
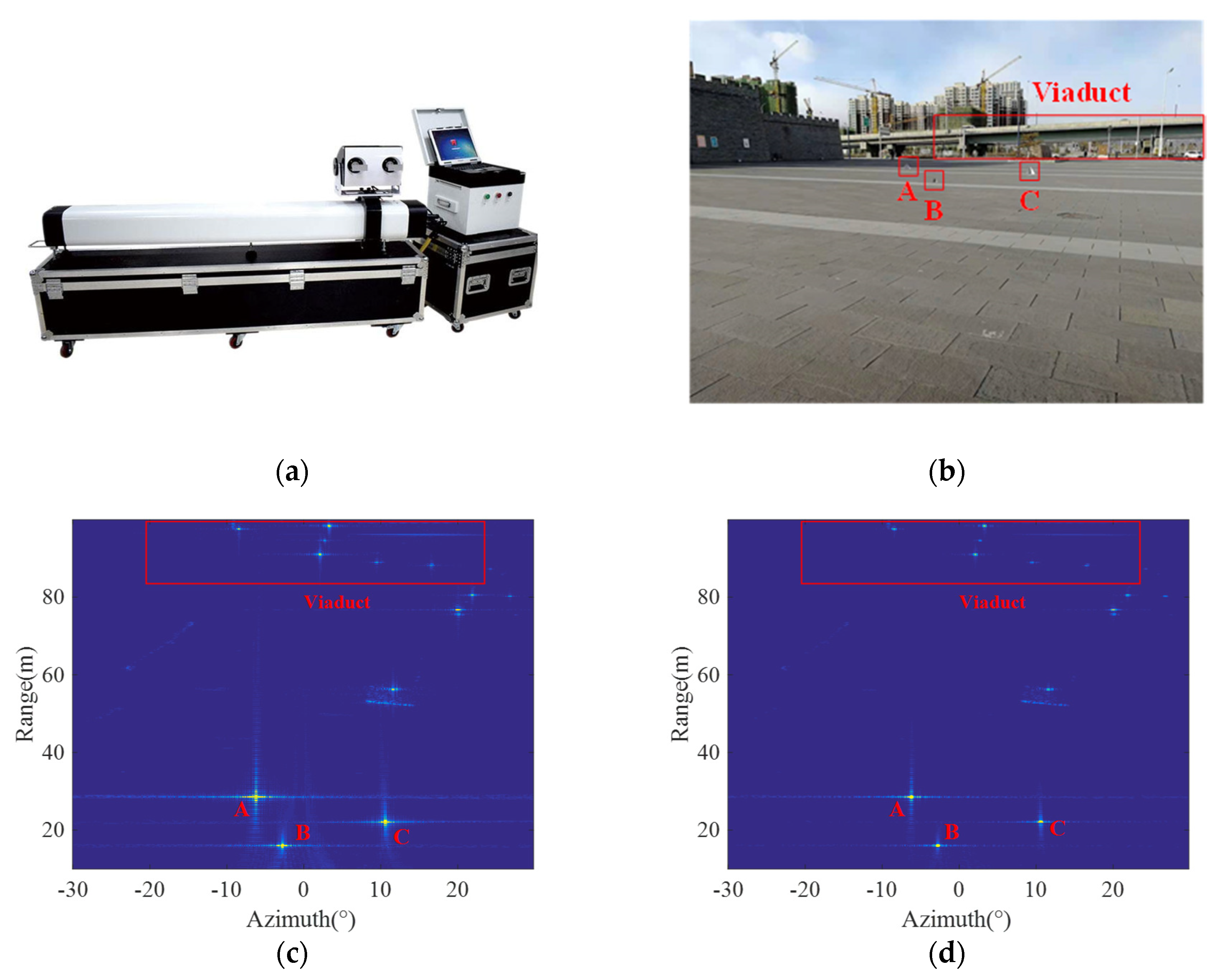
4. Simulation and Results Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xu, W.; Deng, Y.; Wang, R. Multichannel synthetic aperture radar systems with a planar antenna for future spaceborne microwave remote sensing. IEEE Aerosp. Electron. Syst. Mag. 2012, 27, 26–30. [Google Scholar] [CrossRef]
- Jin, G.; Deng, Y.; Wang, R.; Wang, W.; Wang, P.; Long, Y.; Zhang, Z.M.; Zhang, Y. An Advanced Nonlinear Frequency Modulation Waveform for Radar Imaging With Low Sidelobe. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6155–6168. [Google Scholar] [CrossRef]
- Wang, W.; Wang, R.; Deng, Y.; Zhang, Z.; Wu, X.; Xu, Z. Demonstration of NLFM Waveforms With Experiments and Doppler Shift Compensation for SAR Application. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1999–2003. [Google Scholar] [CrossRef]
- Webb, J.L.H.; Munson, D.C.; Stacy, N.J.S. High-resolution planetary imaging via spotlight-mode synthetic aperture radar. IEEE Trans. Image Process. 1998, 7, 1571–1582. [Google Scholar] [CrossRef]
- Luo, X.; Deng, Y.; Wang, R.; Xu, W.; Luo, Y.; Guo, L. Image Formation Processing for Sliding Spotlight SAR with Stepped Frequency Chirps. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1692–1696. [Google Scholar] [CrossRef]
- Wong, F.H.; Tat Soon, Y. A novel technique for the processing of short-dwell spotlight SAR data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 953–963. [Google Scholar] [CrossRef]
- Ge, N.; Gonzalez, F.R.; Wang, Y.; Shi, Y.; Zhu, X.X. Spaceborne Staring Spotlight SAR Tomography—A First Demonstration With TerraSAR-X. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3743–3756. [Google Scholar] [CrossRef] [Green Version]
- Prats-Iraola, P.; Scheiber, R.; Rodriguez-Cassola, M.; Mittermayer, J.; Wollstadt, S.; Zan, F.D.; Bräutigam, B.; Schwerdt, M.; Reigber, A.; Moreira, A. On the Processing of Very High Resolution Spaceborne SAR Data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6003–6016. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Wang, W.; Song, H. Optimization of Weighting Window Functions for SAR Imaging via QCQP Approach. Sensors 2020, 20, 419. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kajenski, P.J. Mismatch filter design via convex optimization. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 1587–1591. [Google Scholar] [CrossRef]
- Davis, M.S.; Lanterman, A.D. Minimum integrated sidelobe ratio filters for MIMO radar. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 405–416. [Google Scholar] [CrossRef]
- Abratkiewicz, K.; Samczyński, P. A Block Method Using the Chirp Rate Estimation for NLFM Radar Pulse Reconstruction. Sensors 2019, 19, 5015. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jin, G.; Liu, K.; Deng, Y.; Sha, Y.; Wang, R.; Liu, D.; Wang, W.; Long, Y.; Zhang, Y. Nonlinear Frequency Modulation Signal Generator in LT-1. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1570–1574. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, W.; Wang, R.; Deng, Y.; Jin, G.; Long, Y. A Novel NLFM Waveform With Low Sidelobes Based on Modified Chebyshev Window. IEEE Geosci. Remote Sens. Lett. 2020, 17, 814–818. [Google Scholar] [CrossRef]
- Xu, W.; Hu, J.; Huang, P.; Tan, W.; Dong, Y. Azimuth Phase Center Adaptive Adjustment upon Reception for High-Resolution Wide-Swath Imaging. Sensors 2019, 19, 4277. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, W.; Wei, Z.; Huang, P.; Tan, W.; Qi, Y.; Gao, Z. Azimuth Multichannel Reconstruction for Moving Targets in Spaceborne Squinted Multichannel Synthetic Aperture Radar. J. Electron. Inf. Technol. 2021, 43, 2276–2285. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, J.; Jin, Y.; Yu, H.; Liang, B.; Yang, D.G. Real-Time Processing of Spaceborne SAR Data With Nonlinear Trajectory Based on Variable PRF. IEEE Trans. Geosci. Remote Sens. 2021, 1–12. [Google Scholar] [CrossRef]
- Villano, M.; Krieger, G.; Moreira, A. Staggered SAR: High-Resolution Wide-Swath Imaging by Continuous PRI Variation. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4462–4479. [Google Scholar] [CrossRef]
- Xiong, Y.; Huang, Y.; Sun, P.; Evan, M.; Cronk, T. A non-uniform sampling tangent type FM demodulation. IEEE Trans. Consum. Electron. 2004, 50, 844–848. [Google Scholar] [CrossRef]
- Zeng, H.C.; Chen, J.; Liu, W.; Yang, W. Modified omega-k algorithm for high-speed platform highly-squint staggered SAR based on azimuth non-uniform interpolation. Sensors 2015, 15, 3750–3765. [Google Scholar] [CrossRef] [Green Version]
- Pang, C.; Hoogeboom, P.; Chevalier, F.L.; Russchenberg, H.W.J.; Dong, J.; Wang, T.; Wang, X. A Pulse Compression Waveform for Weather Radars With Solid-State Transmitters. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2026–2030. [Google Scholar] [CrossRef]
- Zhang, L.; Qiao, Z.; Xing, M.; Yang, L.; Bao, Z. A Robust Motion Compensation Approach for UAV SAR Imagery. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3202–3218. [Google Scholar] [CrossRef]
- Wahl, D.E.; Eichel, P.H.; Ghiglia, D.C.; Jakowatz, C.V. Phase gradient autofocus-a robust tool for high resolution SAR phase correction. IEEE Trans. Aerosp. Electron. Syst. 1994, 30, 827–835. [Google Scholar] [CrossRef] [Green Version]
- Tan, W.; Li, D.; Hong, W. Airborne Spotlight SAR Imaging with Super High Resolution based on Back-Projection and Autofocus Algorithm. In Proceedings of the IGARSS 2008—2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008; pp. IV-1300–IV-1303. [Google Scholar]
- Liu, J.; Tian, X.; Jiang, J.; Huang, K. Distributed Compressed Sensing Based Ground Moving Target Indication for Dual-Channel SAR System. Sensors 2018, 18, 2377. [Google Scholar] [CrossRef] [Green Version]
- Sun, G.-C.; Liu, Y.; Xing, M.; Wang, S.; Guo, L.; Yang, J. A Real-Time Imaging Algorithm Based on Sub-Aperture CS-Dechirp for GF3-SAR Data. Sensors 2018, 18, 2562. [Google Scholar] [CrossRef] [Green Version]
- Huang, P.; Li, K.; Xu, W.; Tan, W.; Gao, Z.; Li, Y. Focusing Arc-Array Bistatic Synthetic Aperture Radar Data Based on Keystone Transform. Electronics 2019, 8, 1389. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Xing, M.; Wang, Y.; Zhang, L.; Bao, Z. Compensation for the NsRCM and Phase Error After Polar Format Resampling for Airborne Spotlight SAR Raw Data of High Resolution. IEEE Geosci. Remote Sens. Lett. 2013, 10, 165–169. [Google Scholar] [CrossRef]
- Li, N.; Wang, R.; Deng, Y.; Chen, J.; Liu, Y.; Zhang, Z.; Zhao, F. MOCO for High-Resolution ScanSAR via Full-Aperture Processing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1721–1726. [Google Scholar] [CrossRef]
- Xu, W.; Deng, Y.; Huang, P.; Wang, R. Full-Aperture SAR Data Focusing in the Spaceborne Squinted Sliding-Spotlight Mode. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4596–4607. [Google Scholar] [CrossRef]
- Ruzanski, E.; Chandrasekar, V. Weather Radar Data Interpolation Using a Kernel-Based Lagrangian Nowcasting Technique. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3073–3083. [Google Scholar] [CrossRef]
- Jin, T.; Qiu, X.; Hu, D.; Ding, C. Unambiguous Imaging of Static Scenes and Moving Targets with the First Chinese Dual-Channel Spaceborne SAR Sensor. Sensors 2017, 17, 1709. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sun, S.; Zhu, G.; Jin, T. Novel Methods to Accelerate CS Radar Imaging by NUFFT. IEEE Trans. Geosci. Remote Sens. 2015, 53, 557–566. [Google Scholar] [CrossRef]
- Xu, W.; Hu, J.; Huang, P.; Tan, W.; Dong, Y. Processing of Multichannel Sliding Spotlight SAR Data with Large Pulse Bandwidth and Azimuth Steering Angle. IEEE Trans. Geosci. Remote Sens. 2021, 1–14. [Google Scholar] [CrossRef]
- Carrara, W.; Goodman, R.; Majewski, R. Spotlight Synthetic Aperture Radar: Signal Processing Algorithms; Artech House: London, UK, 1995. [Google Scholar]
- Moreira, J.R. A New Method Of Aircraft Motion Error Extraction From Radar Raw Data For Real Time Motion Compensation. IEEE Trans. Geosci. Remote Sens. 1990, 28, 620–626. [Google Scholar] [CrossRef]
- Qi, L.; Tan, W.; Huang, P.; Xu, W.; Qi, Y.; Zhang, M. Landslide Prediction Method Based on a Ground-Based Micro-Deformation Monitoring Radar. Remote Sens. 2020, 12, 1230. [Google Scholar] [CrossRef] [Green Version]











| Parameter | Value |
|---|---|
| Pulse duration | 5 μs |
| Pulse bandwidth | 500 MHz |
| Sampling frequency | 600 MHz |
| Carrier frequency | 9.6 GHz |
| Sensor velocity | 150 m/s |
| Length of antenna | 2 m |
| Slant range to the scene center | 30 km |
| Azimuth illumination time | 8 s |
| Number of azimuth samples | 8000 |
| Azimuth average sampling interval | 1 ms |
| Imaging Mode | Target | Range | Azimuth | ||||
|---|---|---|---|---|---|---|---|
| Resolution (m) | PSLR (dB) | ISLR (dB) | Resolution (m) | PSLR (dB) | ISLR (dB) | ||
| The conventional mode | P1 | 0.346 | −13.242 | −10.106 | 0.264 | −13.275 | −10.243 |
| P2 | 0.346 | −13.244 | −10.106 | 0.264 | −13.276 | −10.244 | |
| P3 | 0.346 | −13.243 | −10.106 | 0.264 | −13.276 | −10.244 | |
| Two-dimensional windowing | P1 | 0.450 | −22.959 | −20.489 | 0.312 | −20.292 | −18.626 |
| P2 | 0.450 | −22.964 | −20.871 | 0.312 | −20.319 | −18.489 | |
| P3 | 0.450 | −22.891 | −20.814 | 0.312 | −20.891 | −18.644 | |
| The proposed mode | P1 | 0.406 | −20.2314 | −18.519 | 0.312 | −20.262 | −18.538 |
| P2 | 0.404 | −20.2304 | −18.517 | 0.312 | −20.118 | −18.544 | |
| P3 | 0.404 | −20.228 | −18.516 | 0.312 | −20.126 | −18.516 | |
| Imaging Mode | Range | Azimuth | ||||
|---|---|---|---|---|---|---|
| Resolution (m) | PSLR (dB) | ISLR (dB) | Resolution (m) | PSLR (dB) | ISLR (dB) | |
| The conventional mode | 0.350 | −14.462 | −10.122 | 0.272 | −13.960 | −10.122 |
| The proposed mode | 0.414 | −22.046 | −14.532 | 0.336 | −19.649 | −14.390 |
| Imaging Mode | Range | Azimuth | ||||
|---|---|---|---|---|---|---|
| Resolution (m) | PSLR (dB) | ISLR (dB) | Resolution (°) | PSLR (dB) | ISLR (dB) | |
| The conventional mode | 0.262 | −12.631 | −10.134 | 0.280 | −12.080 | −10.115 |
| The proposed mode | 0.294 | −19.148 | −16.354 | 0.313 | −17.881 | −15.354 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, W.; Zhang, L.; Fang, C.; Huang, P.; Tan, W.; Qi, Y. Staring Spotlight SAR with Nonlinear Frequency Modulation Signal and Azimuth Non-Uniform Sampling for Low Sidelobe Imaging. Sensors 2021, 21, 6487. https://0-doi-org.brum.beds.ac.uk/10.3390/s21196487
Xu W, Zhang L, Fang C, Huang P, Tan W, Qi Y. Staring Spotlight SAR with Nonlinear Frequency Modulation Signal and Azimuth Non-Uniform Sampling for Low Sidelobe Imaging. Sensors. 2021; 21(19):6487. https://0-doi-org.brum.beds.ac.uk/10.3390/s21196487
Chicago/Turabian StyleXu, Wei, Lu Zhang, Chonghua Fang, Pingping Huang, Weixian Tan, and Yaolong Qi. 2021. "Staring Spotlight SAR with Nonlinear Frequency Modulation Signal and Azimuth Non-Uniform Sampling for Low Sidelobe Imaging" Sensors 21, no. 19: 6487. https://0-doi-org.brum.beds.ac.uk/10.3390/s21196487






