Impacts of Dynamic Agglomeration Externalities on Eco-Efficiency: Empirical Evidence from China
Abstract
:1. Introduction
2. Methods, Variables and Data
2.1. Empirical Models
2.2. Variables Specification
2.2.1. Dependent Variable
2.2.2. Interested Variables
2.2.3. Control Variables
2.3. Data
3. Results and Discussion
3.1. Estimation Results of Eco-Efficiency
3.2. Nonlinear Effects of Agglomeration Externalities on Eco-Efficiency
3.2.1. MAR Externalities
3.2.2. Jacobs Externalities
3.2.3. Porter Externalities
3.2.4. Robustness Checks
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| No. | Industries |
|---|---|
| 1 | Primary Industry |
| 2 | Mining |
| 3 | Manufacturing |
| 4 | Production and Distribution of Electricity, Gas and Water |
| 5 | Construction |
| 6 | Wholesale and Retail Trades |
| 7 | Traffic, Transport, Storage and Post |
| 8 | Hotels and Catering Services |
| 9 | Information Transmission, Computer Services and Software |
| 10 | Financial Intermediation |
| 11 | Real Estate |
| 12 | Leasing and Business Services |
| 13 | Scientific Research, Technical Service and Geologic Prospecting |
| 14 | Management of Water Conservancy, Environment |
| 15 | Services to Households and Other Services |
| 16 | Education |
| 17 | Health, Social Security and Social Welfare |
| 18 | Culture, Sports and Entertainment |
| 19 | Public Management and Social Organization |
Appendix B
| Variable | Sources | |
|---|---|---|
| Panel A: DEA model | ||
| Input | Capital | China City Statistical Yearbook and China Statistical Yearbook |
| Input | Labor | China City Statistical Yearbook |
| Input | Land | China City Statistical Yearbook |
| Input | Energy | GDP energy intensity (manually collected from various official documents) multiplied by GDP, China Energy Statistical Yearbook |
| Desirable output | GDP | China City Statistical Yearbook |
| Undesirable output | EPI | China City Statistical Yearbook and China Environment Yearbook |
| Panel B: Econometric model | ||
| Dependent variable | ee | Measured by Model (10) |
| Interest variables | mar | Measured by Model (11), original data from China City Statistical Yearbook |
| jacobs | Measured by Model (12), original data from China City Statistical Yearbook | |
| porter | Measured by Model (13), original data from China City Statistical Yearbook | |
| Control variables | er | China City Statistical Yearbook and China Environment Yearbook |
| lnkl | China City Statistical Yearbook | |
| s_ind | China City Statistical Yearbook | |
| fdi | China City Statistical Yearbook and China Statistical Yearbook | |
| s_tech | China City Statistical Yearbook | |
| s_fiscal | China City Statistical Yearbook | |
| adv_ind | China City Statistical Yearbook | |
References
- Verfaillie, H.A.; Bidwell, R. Measuring Eco-Efficiency: A Guide to Reporting Company Performance; World Business Council for Sustainable Development: Geneva, Switzerland, 2000. [Google Scholar]
- OECD. Eco-Efficiency. In Proceedings of the Conference on Resource Efficiency, Paris, France, 23–25 April 2008. [Google Scholar]
- Waste from Electrical and Electronic Equipment (WEEE). Available online: https://www.eea.europa.eu/data-and-maps/indicators/waste-electrical-and-electronic-equipment/assessment-1 (accessed on 18 October 2018).
- Beltrán-Esteve, M.; Gómez-Limón, J.A.; Picazo-Tadeo, A.J.; Reig-Martínez, E. A metafrontier directional distance function approach to assessing eco-efficiency. J. Prod. Anal. 2014, 41, 69–83. [Google Scholar] [CrossRef]
- Orea, L.; Wall, A. A parametric approach to estimating eco-efficiency. J. Agric. Eco. 2017, 68, 901–907. [Google Scholar] [CrossRef]
- Deng, X.; Gibson, J. Sustainable land use management for improving land eco-efficiency: A case study of Hebei, China. Ann. Oper. Res. 2018. [Google Scholar] [CrossRef]
- Kuosmanen, T.; Kortelainen, M. Measuring eco-efficiency of production with data envelopment analysis. J. Ind. Ecol. 2005, 9, 59–72. [Google Scholar] [CrossRef]
- Zhang, B.; Bi, J.; Fan, Z.; Ge, J. Eco-efficiency analysis of industrial system in China: A data envelopment analysis approach. Ecol. Eco. 2008, 68, 306–316. [Google Scholar] [CrossRef]
- Chen, C.M. Evaluating eco-efficiency with data envelopment analysis: An analytical reexamination. Ann. Oper. Res. 2014, 214, 49–71. [Google Scholar] [CrossRef]
- Rashidi, K.; Saen, R.F. Measuring eco-efficiency based on green indicators and potentials in energy saving and undesirable output abatement. Energy Eco. 2015, 50, 18–26. [Google Scholar] [CrossRef]
- Arabi, B.; Munisamy, S.; Emrouznejad, A.; Toloo, M.; Ghazizadeh, M.S. Eco-efficiency considering the issue of heterogeneity among power plants. Energy 2016, 111, 722–735. [Google Scholar] [CrossRef]
- Beltrán-Esteve, M.; Reig-Martínez, E.; Estruch-Guitart, V. Assessing eco-efficiency: A metafrontier directional distance function approach using life cycle analysis. Environ. Impact Assess. Rev. 2017, 63, 116–127. [Google Scholar] [CrossRef]
- Fan, Y.; Bai, B.; Qiao, Q.; Kang, P.; Zhang, Y. Study on eco-efficiency of industrial parks in China based on data envelopment analysis. J. Environ. Manag. 2017, 192, 107–115. [Google Scholar] [CrossRef] [PubMed]
- Yue, S.; Yang, Y.; Pu, Z. Total-factor ecology efficiency of regions in China. Ecol. Indic. 2017, 73, 284–292. [Google Scholar] [CrossRef]
- Huang, J.; Xia, J.; Yu, Y.; Zhang, N. Composite eco-efficiency indicators for China based on data envelopment analysis. Ecol. Indic. 2018, 85, 674–697. [Google Scholar] [CrossRef]
- Huang, J.; Yu, Y.; Ma, C. Energy Efficiency Convergence in China: Catch-Up, Lock-In and Regulatory Uniformity. Environ. Res. Eco. 2018, 107–130. [Google Scholar] [CrossRef]
- Moutinho, V.; Madaleno, M.; Robaina, M.; Villar, J. Advanced scoring method of eco-efficiency in European cities. Environ. Sci. Pollut. Res. Int. 2018, 25, 1637–1654. [Google Scholar] [CrossRef] [PubMed]
- Fernández, C.; Koop, G.; Steel, M.F.J. Multiple-output production with undesirable outputs. Publ. Am. Stat. Assoc. 2002, 97, 432–442. [Google Scholar] [CrossRef] [Green Version]
- Battese, G.E.; Rao, D.P.; O’Donnell, C.J. A metafrontier production function for estimation of technical efficiencies and technology gaps for firms operating under different technologies. J. Prod. Anal. 2004, 21, 91–103. [Google Scholar] [CrossRef]
- O’Donnell, C.J.; Rao, D.P.; Battese, G.E. Metafrontier frameworks for the study of firm-level efficiencies and technology ratios. Empir. Eco. 2008, 34, 231–255. [Google Scholar] [CrossRef]
- Tiedemann, T.; Francksen, T.; Latacz-Lohmann, U. Assessing the performance of German Bundesliga, football players: A nonparametric metafrontier approach. Central Eur. J. Oper. Res. 2011, 19, 571–587. [Google Scholar] [CrossRef]
- Huang, C.W.; Ting, C.T.; Lin, C.H.; Lin, C.T. Measuring nonconvex metafrontier efficiency in international tourist hotels. J. Oper. Res. Soc. 2013, 64, 250–259. [Google Scholar] [CrossRef]
- Afsharian, M. Metafrontier efficiency analysis with convex and nonconvex metatechnologies by stochastic nonparametric envelopment of data. Eco. Lett. 2017, 160, 1–3. [Google Scholar] [CrossRef]
- Afsharian, M.; Podinovski, V.V. A linear programming approach to efficiency evaluation in nonconvex metatechnologies. Eur. J. Oper. Res. 2018, 268, 268–280. [Google Scholar] [CrossRef]
- Andersen, P.; Petersen, N.C. A procedure for ranking efficient units in data envelopment analysis. Manag. Sci. 1993, 39, 1261–1264. [Google Scholar] [CrossRef]
- Tone, K. A slacks-based measure of super-efficiency in data envelopment analysis. Eur. J. Oper. Res. 2002, 143, 32–41. [Google Scholar] [CrossRef] [Green Version]
- Swann, G.M.P. Technology evolution and the rise and fall of industrial clusters. Rev. Int. Syst. 1996, 10, 285–302. [Google Scholar]
- Glaeser, E.L.; Kallal, H.D.; Scheinkman, J.A.; Shleifer, A. Growth in cities. J. Political Eco. 1992, 100, 1126–1152. [Google Scholar] [CrossRef]
- Melo, P.C.; Graham, D.J.; Noland, R.B. A meta-analysis of estimates of urban agglomeration economies. Reg. Sci. Urban Eco. 2009, 39, 332–342. [Google Scholar] [CrossRef] [Green Version]
- Cerina, F.; Mureddu, F. Is agglomeration really good for growth? Global efficiency, interregional equity and uneven growth. J. Urban Eco. 2014, 84, 9–22. [Google Scholar] [CrossRef]
- Márquez-Ramos, L. The relationship between trade and sustainable transport: A quantitative assessment with indicators of the importance of environmental performance and agglomeration externalities. Ecol. Indic. 2015, 52, 170–183. [Google Scholar] [CrossRef] [Green Version]
- Hu, C.; Xu, Z.; Yashiro, N. Agglomeration and productivity in China: Firm level evidence. China Eco. Rev. 2015, 33, 50–66. [Google Scholar] [CrossRef]
- Zheng, Q.; Lin, B. Impact of industrial agglomeration on energy efficiency in China’s paper industry. J. Clean. Prod. 2018, 184, 1072–1080. [Google Scholar] [CrossRef]
- Han, F.; Xie, R.; Fang, J. Urban agglomeration economics and industrial energy efficiency. Energy 2018, 162, 45–59. [Google Scholar] [CrossRef]
- Hu, A.H.; Shih, S.H.; Hsu, C.W.; Tseng, C.H. Eco-efficiency Evaluation of the Eco-industrial Cluster. In Proceedings of the Fourth International Symposium on Environmentally Conscious Design and Inverse Manufacturing, Tokyo, Japan, 12–14 December 2005. [Google Scholar]
- Li, W.; Xu, Y. Manufacturing agglomeration, environmental technological efficiency and energy-saving and emission-reduction. Eco. Manag. J. 2013, 35, 1–12. (In Chinese) [Google Scholar]
- Shen, N. Can industrial agglomeration improve environmental efficiency? —Spatial empirical test based on city data in China. J. Ind. Eng. Eng. Manag. 2014, 28, 57–63. (In Chinese) [Google Scholar]
- Liu, J.; Cheng, Z.; Zhang, H. Does industrial agglomeration promote the increase of energy efficiency in China? J. Clean. Prod. 2017, 164, 30–37. [Google Scholar] [CrossRef]
- Elhorst, J.P. Spatial econometrics: From cross-sectional data to spatial panels. In Springer Briefs in Regional Science; Springer-Verlag: Berlin, Germany, 2014. [Google Scholar]
- Ke, S.; Xiang, J. Estimation of the fixed capital stocks in Chinese Cities for 1996–2009. Stat. Res. 2012, 29, 1–10. (In Chinese) [Google Scholar]
- Arrow, K. The economic implications of learning by doing. Rev. Eco. Stud. 1962, 29, 155–173. [Google Scholar] [CrossRef]
- Marshall, A. Principles of Economics; Macmillan: London, UK, 1920. [Google Scholar]
- Romer, P.M. Endogenous technological change. J. Political Eco. 1990, 98, 71–102. [Google Scholar] [CrossRef]
- Jacobs, J. The Economy of Cities; Vintage: New York, NY, USA, 1969. [Google Scholar]
- Porter, M.E. The Competitive Advantage of Nations; Free Press: New York, NY, USA, 1990. [Google Scholar]
- Stern, P.C.; Young, O.R.; Druckman, D. Global Environmental Change: Understanding the Human Dimensions; National Academy Press: Washington, DC, USA, 1992. [Google Scholar]
- Dietz, T.; Rosa, E.A. Rethinking the environmental impacts of population, affluence and technology. Hum. Ecol. Rev. 1994, 1, 277–300. [Google Scholar] [CrossRef]
- Ren, S.; Li, X.; Yuan, B.; Li, D.; Chen, X. The effects of three types of environmental regulation on eco-efficiency: A cross-region analysis in China. J. Clean. Prod. 2018, 173, 245–255. [Google Scholar] [CrossRef]
- Javorcik, B.S.; Wei, S.J. Pollution havens and foreign direct investment: Dirty secret or popular myth? Contrib. Eco. Anal. Policy 2001, 3, 1244. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, S.; Zhang, W.; Zhan, D.; Li, J. Does foreign direct investment affect environmental pollution in China’s cities? A spatial econometric perspective. Sci. Total Environ. 2018, 613–614, 521–529. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.T.; Chen, W.Y. Foreign direct investment, institutional development, and environmental externalities: Evidence from China. J. Environ. Manag. 2014, 135, 81–90. [Google Scholar] [CrossRef] [PubMed]
- Tone, K. An epsilon-based measure of efficiency in DEA—A third pole of technical efficiency. Eur. J. Oper. Res. 2010, 207, 1554–1563. [Google Scholar] [CrossRef]
- Simar, L.; Wilson, P.W. Estimation and inference in two-stage, semi-parametric models of production process. J. Eco. 2007, 136, 31–64. [Google Scholar] [CrossRef]
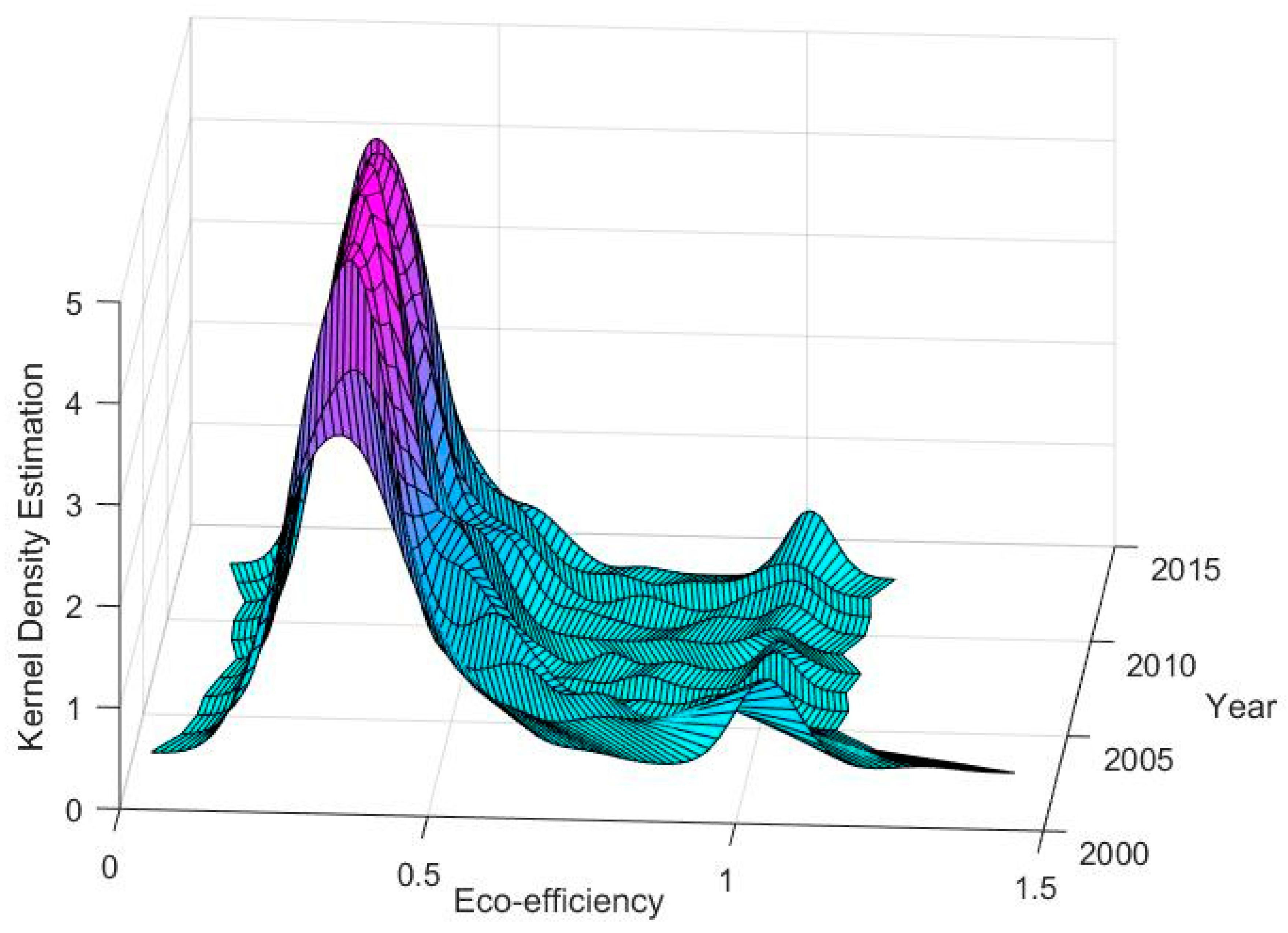
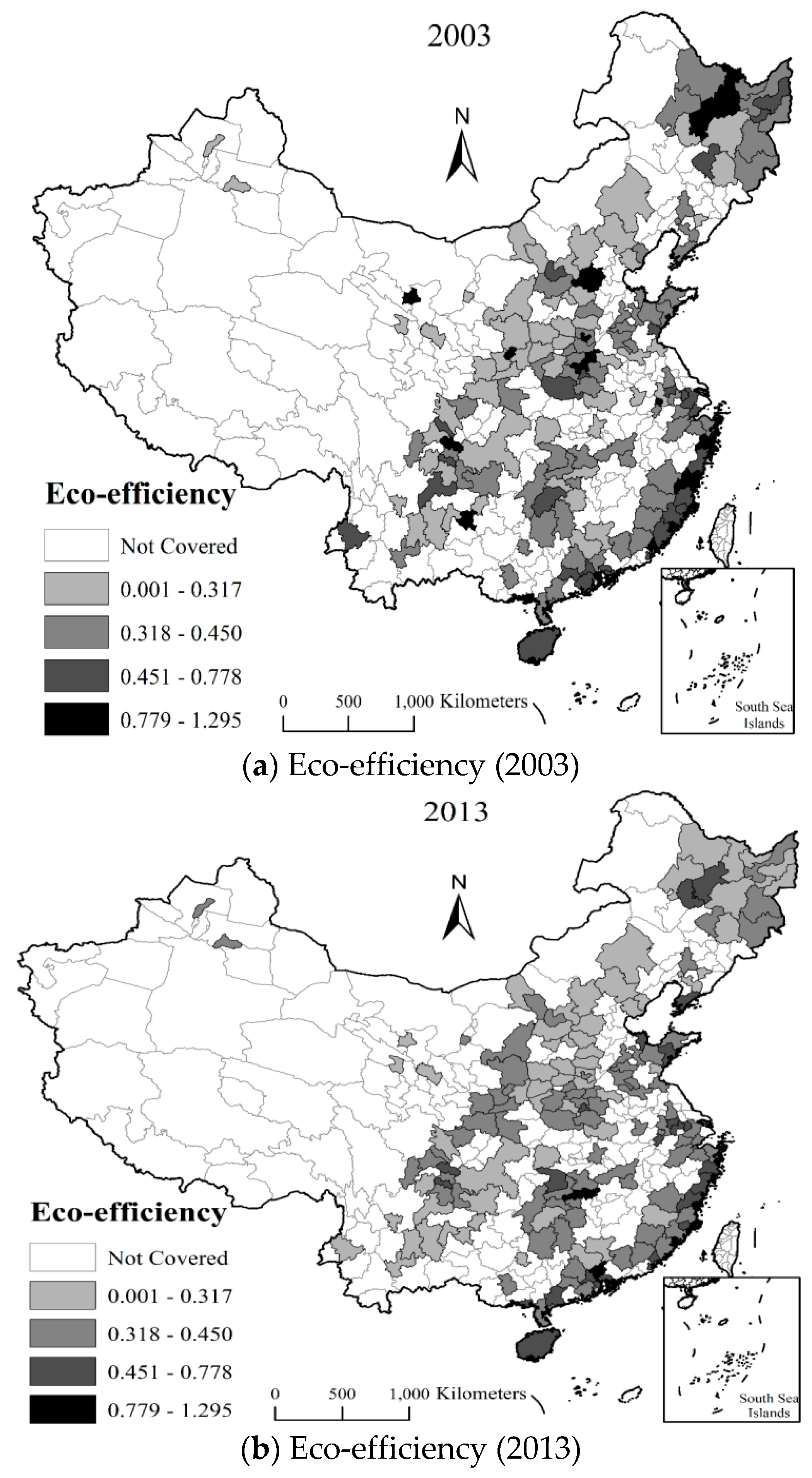
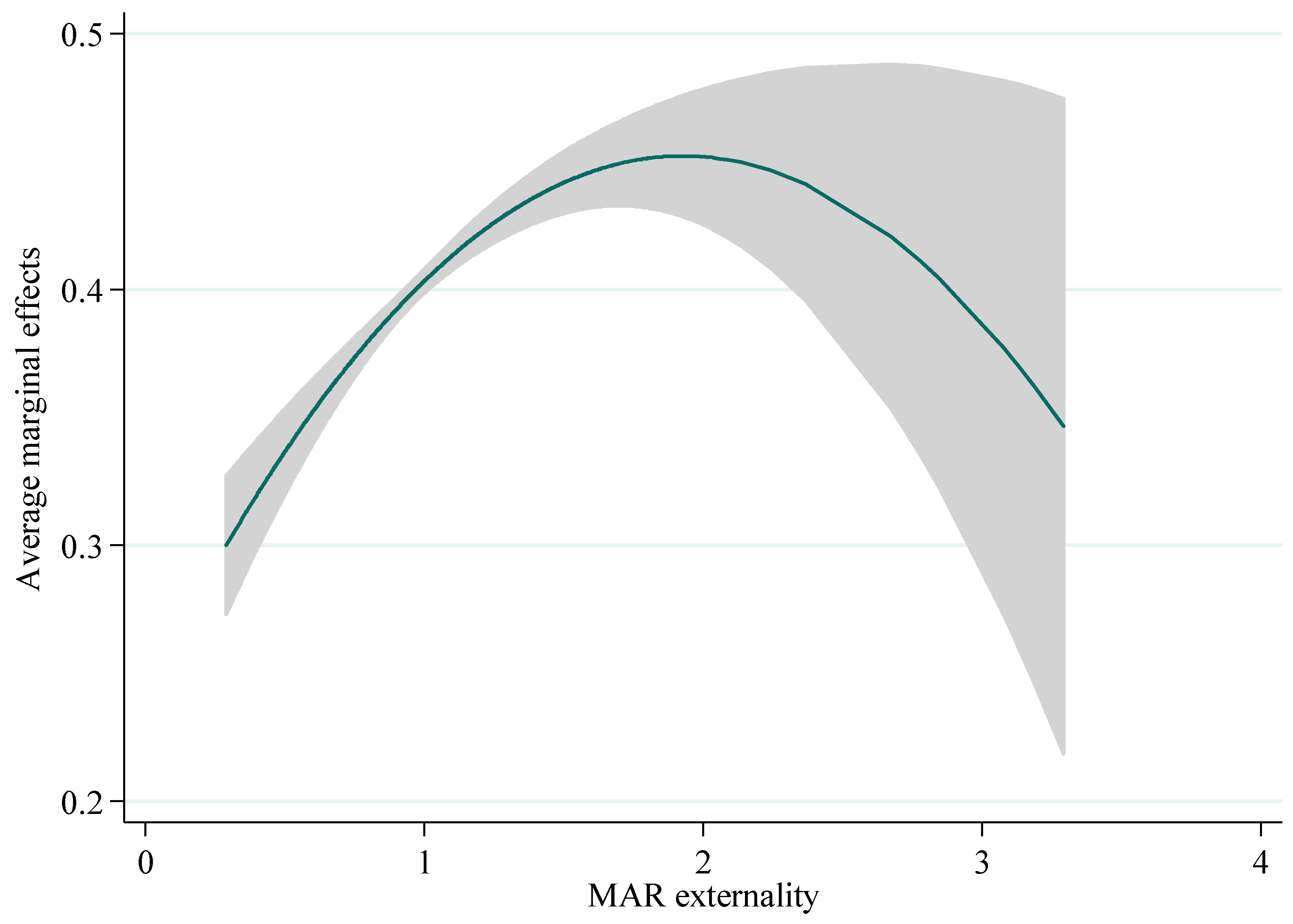


| Variables | Observations | Mean | Standard Deviation | Minimum | Maximum |
|---|---|---|---|---|---|
| ee | 2101 | 0.40344 | 0.1734 | 0.1735 | 1.2950 |
| mar | 2101 | 1.0239 | 0.3360 | 0.2891 | 3.2944 |
| jacobs | 2101 | 1.0907 | 0.1080 | 0.4273 | 3.6675 |
| porter | 2101 | 0.9909 | 0.0703 | 0.4460 | 1.0349 |
| er | 2101 | 0.3799 | 0.2634 | 0.0100 | 0.9900 |
| lnkl | 2101 | 3.7291 | 0.6718 | 1.5839 | 5.4519 |
| s_ind | 2101 | 0.4965 | 0.1160 | 0.1570 | 0.9097 |
| fdi | 2101 | 0.1672 | 0.1770 | 0.0000 | 0.8554 |
| s_tech | 2101 | 9.2000 | 1.8684 | −2.0402 | 14.7620 |
| s_fiscal | 2101 | 0.1354 | 0.0774 | 0.0154 | 1.5642 |
| adv_ind | 2101 | 0.8191 | 0.4199 | 0.0943 | 3.4431 |
| Variables | (1) | (2) | (3) | (4) | (5) | (6) | (7) |
|---|---|---|---|---|---|---|---|
| mar | 0.1435 *** | 0.2342 *** | 0.2180 *** | 0.2115 *** | 0.2151 *** | 0.2153 *** | 0.2184 *** |
| (3.7178) | (6.1650) | (5.7168) | (5.5268) | (5.6864) | (5.7151) | (5.8553) | |
| mar × mar | −0.0501 *** | −0.0618 *** | −0.0576 *** | −0.0552 *** | −0.0549 *** | −0.0550 *** | −0.0566 *** |
| (−3.2915) | (−4.2044) | (−3.9205) | (−3.7430) | (−3.7606) | (−3.7858) | (−3.9368) | |
| er | 0.0245 ** | 0.0356 *** | 0.0315 *** | 0.0315 *** | 0.0323 *** | 0.0277 ** | 0.0272 ** |
| (2.0914) | (3.1396) | (2.7687) | (2.7768) | (2.8746) | (2.4631) | (2.4444) | |
| lnkl | −0.1204 *** | −0.1073 *** | −0.1054 *** | −0.1107 *** | −0.1086 *** | −0.1094 *** | |
| (−11.9921) | (−10.0859) | (−9.8688) | (−10.4524) | (−10.2909) | (−10.4739) | ||
| s_ind | −0.0020 *** | −0.0020 *** | −0.0014 ** | −0.0012 ** | 0.0033 *** | ||
| (−3.6538) | (−3.6597) | (−2.5519) | (−2.2403) | (3.6852) | |||
| fdi | −0.0650 * | −0.0599 * | −0.0564 | −0.0535 | |||
| (−1.8433) | (−1.7180) | (−1.6230) | (−1.5547) | ||||
| s_tech | 0.0260 *** | 0.0248 *** | 0.0228 *** | ||||
| (6.6858) | (6.3891) | (5.9027) | |||||
| s_fiscal | −0.1875 *** | −0.1723 *** | |||||
| (−4.1328) | (−3.8310) | ||||||
| adv_ind | 0.1305 *** | ||||||
| (6.2904) | |||||||
| Constant | 0.3524 *** | 0.6168 *** | 0.6845 *** | 0.6939 *** | 0.4970 *** | 0.5105 *** | 0.1980 *** |
| (14.3915) | (19.0922) | (18.4234) | (18.5142) | (10.4993) | (10.8041) | (2.9028) | |
| Observations | 2101 | 2101 | 2101 | 2101 | 2101 | 2101 | 2101 |
| R-squared | 0.0570 | 0.1235 | 0.1296 | 0.1312 | 0.1512 | 0.1588 | 0.1761 |
| Variables | (1) | (2) | (3) | (4) |
|---|---|---|---|---|
| SAR | SEM | SDM | SAC | |
| mar | 0.1357 *** | 0.2096 *** | 0.2195 *** | 0.2129 *** |
| (3.8948) | (5.8970) | (6.1386) | (6.0067) | |
| mar × mar | −0.0381 *** | −0.0533 *** | −0.0554 *** | −0.0544 *** |
| (−2.7587) | (−3.9334) | (−4.0550) | (−4.0190) | |
| er | 0.0412 *** | 0.0305 *** | 0.0275 ** | 0.0298 *** |
| (3.9259) | (2.8544) | (2.5539) | (2.7971) | |
| lnkl | −0.0341 *** | −0.1024 *** | −0.1178 *** | −0.1062 *** |
| (−6.1976) | (−9.4003) | (−10.4331) | (−9.8139) | |
| s_ind | 0.0031 *** | 0.0033 *** | 0.0038 *** | 0.0033 *** |
| (3.5797) | (3.6462) | (3.9384) | (3.6293) | |
| fdi | −0.0939 *** | −0.0759 ** | −0.0768 ** | −0.0758 ** |
| (−2.8561) | (−2.3043) | (−2.3158) | (−2.3055) | |
| s_tech | 0.0072 *** | 0.0189 *** | 0.0194 *** | 0.0193 *** |
| (5.0399) | (5.6194) | (5.1221) | (5.6206) | |
| s_fiscal | −0.0981 ** | −0.1442 *** | −0.1522 *** | −0.1498 *** |
| (−2.3284) | (−3.3580) | (−3.5051) | (−3.4871) | |
| adv_ind | 0.1520 *** | 0.1374 *** | 0.1408 *** | 0.1367 *** |
| (7.6580) | (6.8041) | (6.8227) | (6.7770) | |
| W × mar | −0.3485 | |||
| (−1.2775) | ||||
| W × mar × mar | 0.1024 | |||
| (0.9318) | ||||
| W × er | 0.0269 | |||
| (0.4266) | ||||
| W × lnkl | 0.1132 *** | |||
| (4.8679) | ||||
| W × s_ind | −0.0107 * | |||
| (−1.9159) | ||||
| W × fdi | 0.1147 | |||
| (0.5592) | ||||
| W × s_tech | −0.0187 *** | |||
| (−4.4343) | ||||
| W × s_fiscal | 0.0296 | |||
| (0.1263) | ||||
| W × adv_ind | −0.3241 ** | |||
| (−2.1923) | ||||
| ρ | 0.5872 *** | 0.6628 *** | −0.2671 * | |
| (8.4240) | (9.2129) | (−1.7694) | ||
| λ | 0.8276 *** | 0.8464 *** | ||
| (21.8569) | (24.2155) | |||
| Observations | 2101 | 2101 | 2101 | 2101 |
| R-squared | 0.0003 | 0.0023 | 0.0056 | 0.0023 |
| Variables | (1) | (2) | (3) | (4) | (5) | (6) | (7) |
|---|---|---|---|---|---|---|---|
| jacobs | 0.7372 *** | 0.6376 *** | 0.6036 *** | 0.5811 *** | 0.5545 *** | 0.5357 *** | 0.4416 *** |
| (6.3861) | (5.6131) | (5.3276) | (5.1026) | (4.9114) | (4.7592) | (3.9080) | |
| jacobs × jacobs | −0.1587 *** | −0.1413 *** | −0.1346 *** | −0.1277 *** | −0.1201 *** | −0.1158 *** | −0.0962 *** |
| (−5.7847) | (−5.2476) | (−5.0143) | (−4.7129) | (−4.4732) | (−4.3240) | (−3.5882) | |
| er | 0.0282 ** | 0.0377 *** | 0.0325 *** | 0.0325 *** | 0.0330 *** | 0.0286 ** | 0.0282 ** |
| (2.4270) | (3.2996) | (2.8476) | (2.8428) | (2.9172) | (2.5258) | (2.5109) | |
| lnkl | −0.0836 *** | −0.0709 *** | −0.0693 *** | −0.0726 *** | −0.0707 *** | −0.0724 *** | |
| (−9.0490) | (−7.3534) | (−7.1640) | (−7.5643) | (−7.3945) | (−7.6238) | ||
| s_ind | −0.0024 *** | −0.0024 *** | −0.0019 *** | −0.0017 *** | 0.0024 ** | ||
| (−4.4114) | (−4.4039) | (−3.4254) | (−3.1365) | (2.5776) | |||
| fdi | −0.0660 * | −0.0634 * | −0.0607 * | −0.0601 * | |||
| (−1.8405) | (−1.7835) | (−1.7138) | (−1.7106) | ||||
| s_tech | 0.0240 *** | 0.0229 *** | 0.0212 *** | ||||
| (6.1254) | (5.8496) | (5.4302) | |||||
| s_fiscal | −0.1788 *** | −0.1667 *** | |||||
| (−3.9037) | (−3.6642) | ||||||
| adv_ind | 0.1174 *** | ||||||
| (5.5255) | |||||||
| Constant | −0.1712 * | 0.1560 | 0.2610 ** | 0.2835 *** | 0.1228 | 0.1514 | −0.0454 |
| (−1.8071) | (1.5664) | (2.5607) | (2.7632) | (1.1700) | (1.4446) | (−0.4133) | |
| Observations | 2101 | 2101 | 2101 | 2101 | 2101 | 2101 | 2101 |
| R-squared | 0.0708 | 0.1092 | 0.1183 | 0.1199 | 0.1370 | 0.1439 | 0.1575 |
| Variables | (1) | (2) | (3) | (4) |
|---|---|---|---|---|
| SAR | SEM | SDM | SAC | |
| jacobs | 0.4645 *** | 0.4434 *** | 0.4237 *** | 0.4407 *** |
| (4.3217) | (4.1583) | (3.9687) | (4.1377) | |
| jacobs × jacobs | −0.0999 *** | −0.0959 *** | −0.0915 *** | −0.0953 *** |
| (−3.9169) | (−3.7890) | (−3.6112) | (−3.7720) | |
| er | 0.0381 *** | 0.0321 *** | 0.0301 *** | 0.0316 *** |
| (3.6414) | (2.9873) | (2.7705) | (2.9406) | |
| lnkl | −0.0290 *** | −0.0668 *** | −0.0802 *** | −0.0700 *** |
| (−5.3511) | (−7.3375) | (−7.6727) | (−7.3879) | |
| s_ind | 0.0023 *** | 0.0023 ** | 0.0026 *** | 0.0023 ** |
| (2.6026) | (2.4782) | (2.6257) | (2.4656) | |
| fdi | −0.0872 *** | −0.0790 ** | −0.0830 ** | −0.0790 ** |
| (−2.6220) | (−2.3430) | (−2.4414) | (−2.3443) | |
| s_tech | 0.0065 *** | 0.0164 *** | 0.0190 *** | 0.0170 *** |
| (4.5769) | (5.1024) | (4.9530) | (5.1019) | |
| s_fiscal | −0.1096 *** | −0.1470 *** | −0.1564*** | −0.1513 *** |
| (−2.6043) | (−3.4023) | (−3.5625) | (−3.4895) | |
| adv_ind | 0.1310 *** | 0.1251 *** | 0.1292 *** | 0.1246 *** |
| (6.5071) | (6.0552) | (6.0911) | (6.0292) | |
| W × jacobs | −1.2180 | |||
| (−1.3419) | ||||
| W × jacobs × jacobs | 0.2487 | |||
| (1.1219) | ||||
| W × er | 0.0295 | |||
| (0.4672) | ||||
| W × lnkl | 0.0726 *** | |||
| (3.0637) | ||||
| W × s_ind | −0.0087 * | |||
| (−1.6580) | ||||
| W × fdi | 0.1049 | |||
| (0.4906) | ||||
| W × s_tech | −0.0190 *** | |||
| (−4.4550) | ||||
| W × s_fiscal | 0.0742 | |||
| (0.3144) | ||||
| W × adv_ind | −0.3250 ** | |||
| (−2.2213) | ||||
| ρ | 0.6135 *** | 0.6479 *** | −0.1765 | |
| (8.9971) | (8.8285) | (−1.1106) | ||
| λ | 0.7570 *** | 0.7882 *** | ||
| (14.5573) | (15.1576) | |||
| Observations | 2101 | 2101 | 2101 | 2101 |
| R-squared | 0.0000 | 0.0008 | 0.0004 | 0.0008 |
| Varibles | (1) | (2) | (3) | (4) | (5) | (6) | (7) |
|---|---|---|---|---|---|---|---|
| porter | 2.2885 *** | 2.0824 *** | 2.0929 *** | 2.0566 *** | 1.7181 *** | 1.3774 ** | 1.3198 ** |
| (3.3876) | (3.1569) | (3.1913) | (3.1383) | (2.6359) | (2.1008) | (2.0317) | |
| porter × porter | −1.3865 *** | −1.1325 *** | −1.1335 *** | −1.1136 *** | −0.9131 ** | −0.7048 * | −0.6918 * |
| (−3.3932) | (−2.8337) | (−2.8531) | (−2.8049) | (−2.3129) | (−1.7745) | (−1.7580) | |
| er | 0.0244 ** | 0.0347 *** | 0.0290 ** | 0.0291 ** | 0.0302 *** | 0.0264 ** | 0.0261 ** |
| (2.0766) | (3.0156) | (2.5218) | (2.5273) | (2.6481) | (2.3164) | (2.3109) | |
| lnkl | −0.0925 *** | −0.0783 *** | −0.0764 *** | −0.0797 *** | −0.0782 *** | −0.0785 *** | |
| (−9.7760) | (−7.9459) | (−7.7331) | (−8.1300) | (−7.9924) | (−8.0961) | ||
| s_ind | −0.0026 *** | −0.0026 *** | −0.0021 *** | −0.0019 *** | 0.0025 *** | ||
| (−4.8346) | (−4.8205) | (−3.8407) | (−3.5369) | (2.7683) | |||
| fdi | −0.0780 ** | −0.0740 ** | −0.0711 ** | −0.0688 ** | |||
| (−2.1993) | (−2.1068) | (−2.0305) | (−1.9827) | ||||
| s_tech | 0.0237 *** | 0.0227 *** | 0.0208 *** | ||||
| (6.0007) | (5.7711) | (5.3108) | |||||
| s_fiscal | −0.1765 *** | −0.1619 *** | |||||
| (−3.8061) | (−3.5181) | ||||||
| adv_ind | 0.1277 *** | ||||||
| (6.0631) | |||||||
| Constant | −0.4550 * | −0.2377 | −0.1643 | −0.1409 | −0.1820 | −0.0379 | −0.3003 |
| (−1.6504) | (−0.8804) | (−0.6110) | (−0.5242) | (−0.6833) | (−0.1415) | (−1.1157) | |
| Observations | 2101 | 2101 | 2101 | 2101 | 2101 | 2101 | 2101 |
| R-squared | 0.0555 | 0.1009 | 0.1118 | 0.1141 | 0.1306 | 0.1372 | 0.1537 |
| Variables | (1) | (2) | (3) | (4) |
|---|---|---|---|---|
| SAR | SEM | SDM | SAC | |
| porter | 1.5022 ** | 1.3467 ** | 1.4023 ** | 1.3593 ** |
| (2.4272) | (2.1408) | (2.1950) | (2.1626) | |
| porter × porter | −0.8672 ** | −0.7198 * | −0.7473 * | −0.7218 * |
| (−2.3192) | (−1.8914) | (−1.9359) | (−1.8986) | |
| er | 0.0363 *** | 0.0312 *** | 0.0290 *** | 0.0306 *** |
| (3.4493) | (2.8901) | (2.6445) | (2.8376) | |
| lnkl | −0.0308 *** | −0.0714 *** | −0.0860 *** | −0.0754 *** |
| (−5.6670) | (−7.5397) | (−8.0963) | (−7.6883) | |
| s_ind | 0.0026 *** | 0.0026 *** | 0.0030 *** | 0.0025 *** |
| (2.9425) | (2.7724) | (3.0362) | (2.7481) | |
| fdi | −0.0962 *** | −0.0887 *** | −0.0924 *** | −0.0887 *** |
| (−2.9199) | (−2.6658) | (−2.7567) | (−2.6678) | |
| s_tech | 0.0065 *** | 0.0164 *** | 0.0187 *** | 0.0171 *** |
| (4.5671) | (5.0966) | (4.8585) | (5.1068) | |
| s_fiscal | −0.0999 ** | −0.1412 *** | −0.1535 *** | −0.1464 *** |
| (−2.3472) | (−3.2300) | (−3.4596) | (−3.3397) | |
| adv_ind | 0.1445 *** | 0.1373 *** | 0.1434 *** | 0.1365 *** |
| (7.2570) | (6.7067) | (6.8422) | (6.6639) | |
| W × porter | −1.8517 | |||
| (−0.3943) | ||||
| W × porter × porter | 1.2462 | |||
| (0.4217) | ||||
| W × er | 0.0021 | |||
| (0.0333) | ||||
| W × lnkl | 0.0893 *** | |||
| (3.7885) | ||||
| W × s_ind | −0.0106 * | |||
| (−1.8671) | ||||
| W × fdi | 0.1215 | |||
| (0.5800) | ||||
| W × s_tech | −0.0185 *** | |||
| (−4.3363) | ||||
| W × s_fiscal | 0.1069 | |||
| (0.4165) | ||||
| W × adv_ind | −0.3703 ** | |||
| (−2.3935) | ||||
| ρ | 0.5971 *** | 0.6470 *** | −0.2124 | |
| (8.5988) | (8.8090) | (−1.3408) | ||
| λ | 0.7614 *** | 0.7960 *** | ||
| (14.7100) | (16.0125) | |||
| Observations | 2101 | 2101 | 2101 | 2101 |
| R-squared | 0.0007 | 0.0033 | 0.0071 | 0.0034 |
| Vaaribles | (1) | (2) | (3) |
|---|---|---|---|
| mar | 0.1900 *** | ||
| (5.8564) | |||
| mar × mar | −0.0383 *** | ||
| (−3.0635) | |||
| jacobs | 0.2147 ** | ||
| (2.1597) | |||
| jacobs × jacobs | −0.0471 ** | ||
| (−1.9975) | |||
| porter | 1.1929 ** | ||
| (2.1012) | |||
| porter × porter | −0.5063 | ||
| (−1.4722) | |||
| er | 0.0302 *** | 0.0299 *** | 0.0281 *** |
| (3.1159) | (3.0228) | (2.8466) | |
| lnkl | −0.1552 *** | −0.1148 *** | −0.1233 *** |
| (−17.0801) | (−13.7358) | (−14.5606) | |
| s_ind | 0.0057 *** | 0.0048 *** | 0.0047 *** |
| (7.2134) | (6.0233) | (5.9408) | |
| fdi | −0.0461 | −0.0553 * | −0.0579 * |
| (−1.5399) | (−1.7897) | (−1.9083) | |
| s_tech | 0.0264 *** | 0.0246 *** | 0.0241 *** |
| (7.8681) | (7.1695) | (7.0526) | |
| s_fiscal | −0.2349 *** | −0.2327 *** | −0.2279 *** |
| (−6.0049) | (−5.8108) | (−5.6672) | |
| adv_ind | 0.1257 *** | 0.1203 *** | 0.1213 *** |
| (6.9670) | (6.4354) | (6.5868) | |
| Constant | 0.4126 *** | 0.3288 *** | −0.1452 |
| (6.9519) | (3.3992) | (−0.6173) | |
| Observations | 2101 | 2101 | 2101 |
| R-squared | 0.2723 | 0.2384 | 0.2454 |
| Variables | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) |
|---|---|---|---|---|---|---|---|---|---|
| Adding Lag Term of Eco-Efficiency | Adding Lag Terms of Externalities | Adding Front Terms of Externalities | |||||||
| Lagged (EE) | 0.6836 *** | 0.6837 *** | 0.6860 *** | ||||||
| (51.0342) | (52.0274) | (52.1612) | |||||||
| mar | 0.0148 | 0.2358 *** | 0.1785 *** | ||||||
| (0.6914) | (6.4432) | (4.8017) | |||||||
| mar × mar | −0.0027 | −0.0752 *** | −0.0515 *** | ||||||
| (−0.3356) | (−5.1120) | (−3.5162) | |||||||
| jacobs | 0.1823 *** | 1.1729 *** | 0.3367 *** | ||||||
| (2.9917) | (3.5881) | (3.0344) | |||||||
| jacobs × jacobs | −0.0405 *** | −0.4532 *** | −0.0728 *** | ||||||
| (−2.8052) | (−3.0639) | (−2.7876) | |||||||
| porter | 0.1820 | 0.6265 | 1.1749 * | ||||||
| (0.4688) | (1.0891) | (1.6601) | |||||||
| porter × porter | −0.0628 | −0.3690 | −0.7221 * | ||||||
| (−0.2653) | (−1.0585) | (−1.6757) | |||||||
| er | 0.0213 *** | 0.0213 *** | 0.0209 *** | 0.0187 * | 0.0239 ** | 0.0232 ** | 0.0187 | 0.0177 | 0.0162 |
| (3.3853) | (3.3895) | (3.3134) | (1.8659) | (2.3592) | (2.2757) | (1.5667) | (1.4741) | (1.3429) | |
| lnkl | −0.0278 *** | −0.0233 *** | −0.0261 *** | −0.0917 *** | −0.0749 *** | −0.0735 *** | −0.0739 *** | −0.0609 *** | −0.0616 *** |
| (−4.2614) | (−4.0918) | (−4.4399) | (−9.8755) | (−8.2368) | (−8.0815) | (−6.8337) | (−5.7010) | (−5.7375) | |
| s_ind | 0.0024 *** | 0.0022 *** | 0.0023 *** | 0.0036 *** | 0.0029 *** | 0.0032 *** | 0.0018 * | 0.0012 | 0.0015 |
| (4.5221) | (4.1705) | (4.3404) | (4.2593) | (3.4189) | (3.6392) | (1.8950) | (1.2755) | (1.5137) | |
| fdi | −0.0674 *** | −0.0630 *** | −0.0678 *** | −0.0899 *** | −0.0954 *** | −0.0987 *** | 0.0654 | 0.0513 | 0.0441 |
| (−3.4860) | (−3.2300) | (−3.5238) | (−2.9328) | (−3.0850) | (−3.1793) | (1.2119) | (0.9448) | (0.8108) | |
| s_tech | 0.0031 | 0.0030 | 0.0029 | 0.0174 *** | 0.0171 *** | 0.0164 *** | 0.0177 *** | 0.0172 *** | 0.0168 *** |
| (1.4083) | (1.3435) | (1.3169) | (4.9700) | (4.8251) | (4.6155) | (4.5768) | (4.4189) | (4.2912) | |
| s_fiscal | 0.0345 | 0.0364 | 0.0352 | −0.0931 ** | −0.0908 ** | −0.0892 ** | −0.6770 *** | −0.6677 *** | −0.6568 *** |
| (1.3920) | (1.4730) | (1.4089) | (−2.3757) | (−2.2922) | (−2.2276) | (−9.1757) | (−8.9903) | (−8.7431) | |
| adv_ind | 0.0598 *** | 0.0545 *** | 0.0582 *** | 0.1336 *** | 0.1190 *** | 0.1313 *** | 0.0973 *** | 0.0831 *** | 0.0948 *** |
| (4.8843) | (4.4191) | (4.7449) | (6.9050) | (5.9770) | (6.5399) | (4.4150) | (3.6867) | (4.2614) | |
| Constant | −0.0077 | −0.1446 ** | −0.1115 | 0.0904 | −0.4939 ** | −0.0314 | 0.2963 *** | 0.1509 | −0.0365 |
| (−0.1731) | (−2.2645) | (−0.6986) | (1.2686) | (−2.5725) | (−0.1320) | (4.0137) | (1.3640) | (−0.1252) | |
| Observations | 1910 | 1910 | 1910 | 1910 | 1910 | 1910 | 1910 | 1910 | 1910 |
| R-squared | 0.6681 | 0.6696 | 0.6682 | 0.1601 | 0.1434 | 0.1350 | 0.1879 | 0.1760 | 0.1728 |
| Variables | (1) | (2) | (3) |
|---|---|---|---|
| mar | 0.0575 *** | ||
| (4.6039) | |||
| mar × mar | −0.1027 *** | ||
| (−3.4084) | |||
| jacobs | 0.0771 *** | ||
| (3.2387) | |||
| jacobs × jacobs | −0.4410 *** | ||
| (−6.0581) | |||
| porter | 0.4212 | ||
| (1.1068) | |||
| porter × porter | −0.2649 | ||
| (−1.1299) | |||
| er | −0.0162 | −0.0201 * | −0.0198 * |
| (−1.4483) | (−1.7699) | (−1.7694) | |
| lnkl | −0.0007 | 0.0030 | 0.0043 |
| (−0.1266) | (0.5833) | (0.8308) | |
| s_ind | 0.0010 ** | 0.0008 * | 0.0010 ** |
| (2.2315) | (1.9517) | (2.2093) | |
| fdi | 0.2608 *** | 0.2901 *** | 0.2748 *** |
| (15.2070) | (17.2982) | (16.2549) | |
| s_tech | −0.0009 | 0.0023 | −0.0016 |
| (−0.5454) | (1.3780) | (−0.9603) | |
| s_fiscal | −0.0906 ** | −0.1621 *** | −0.0931 ** |
| (−2.1876) | (−3.9534) | (−2.2885) | |
| adv_ind | 0.0371 *** | 0.0425 *** | 0.0395 *** |
| (3.0956) | (3.6846) | (3.2518) | |
| Constant | 0.3216 *** | 0.6384 *** | 0.1114 |
| (8.8120) | (10.5686) | (0.7184) | |
| Observations | 2101 | 2101 | 2101 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Y.; Zhang, Y.; Miao, X. Impacts of Dynamic Agglomeration Externalities on Eco-Efficiency: Empirical Evidence from China. Int. J. Environ. Res. Public Health 2018, 15, 2304. https://0-doi-org.brum.beds.ac.uk/10.3390/ijerph15102304
Yu Y, Zhang Y, Miao X. Impacts of Dynamic Agglomeration Externalities on Eco-Efficiency: Empirical Evidence from China. International Journal of Environmental Research and Public Health. 2018; 15(10):2304. https://0-doi-org.brum.beds.ac.uk/10.3390/ijerph15102304
Chicago/Turabian StyleYu, Yantuan, Yun Zhang, and Xiao Miao. 2018. "Impacts of Dynamic Agglomeration Externalities on Eco-Efficiency: Empirical Evidence from China" International Journal of Environmental Research and Public Health 15, no. 10: 2304. https://0-doi-org.brum.beds.ac.uk/10.3390/ijerph15102304





