Comparison of Thermal Response for RF Exposure in Human and Rat Models
Abstract
:1. Introduction
2. Models and Methods
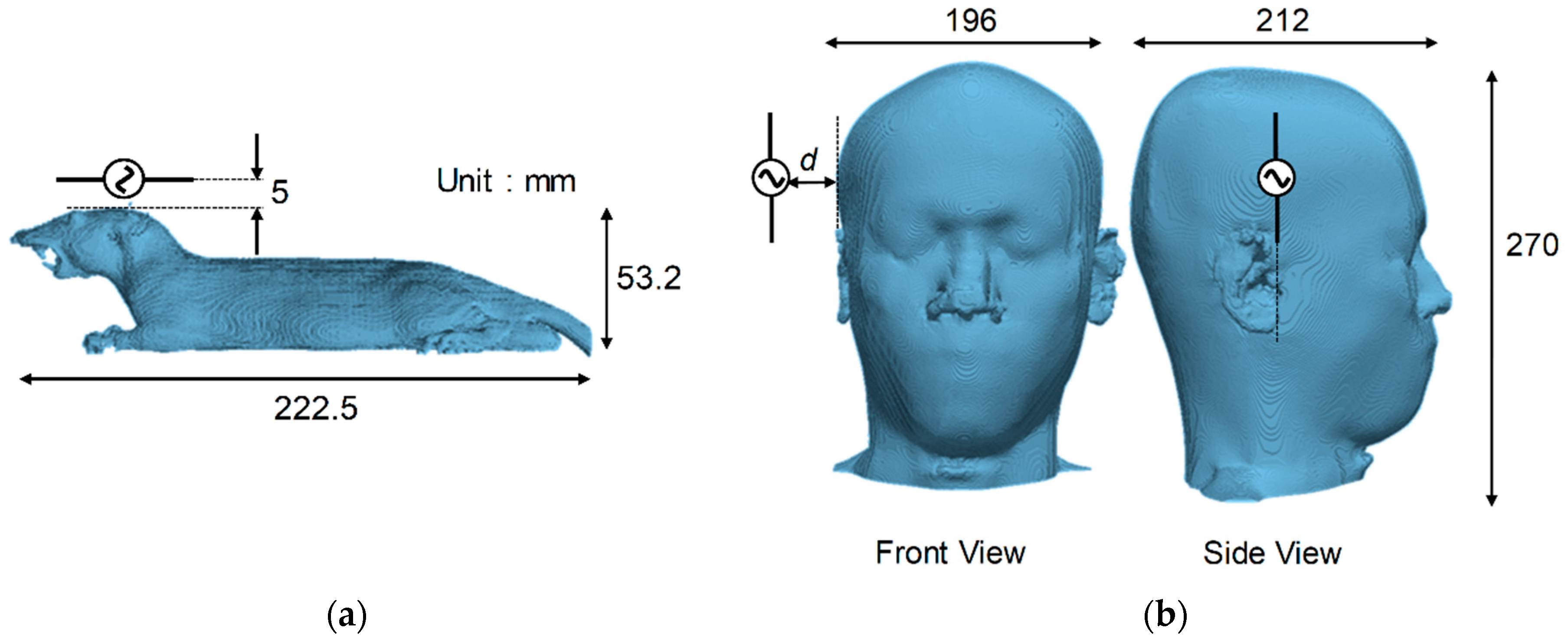
2.1. Computational Rat and Human Models
2.2. Computational Models
2.2.1. SAR Computation
2.2.2. Temperature Computation
2.2.3. Exposure Scenarios
2.2.4. Definition of Thermal Time Constant
2.2.5. Definition of Effective SAR volume
3. Computational Results
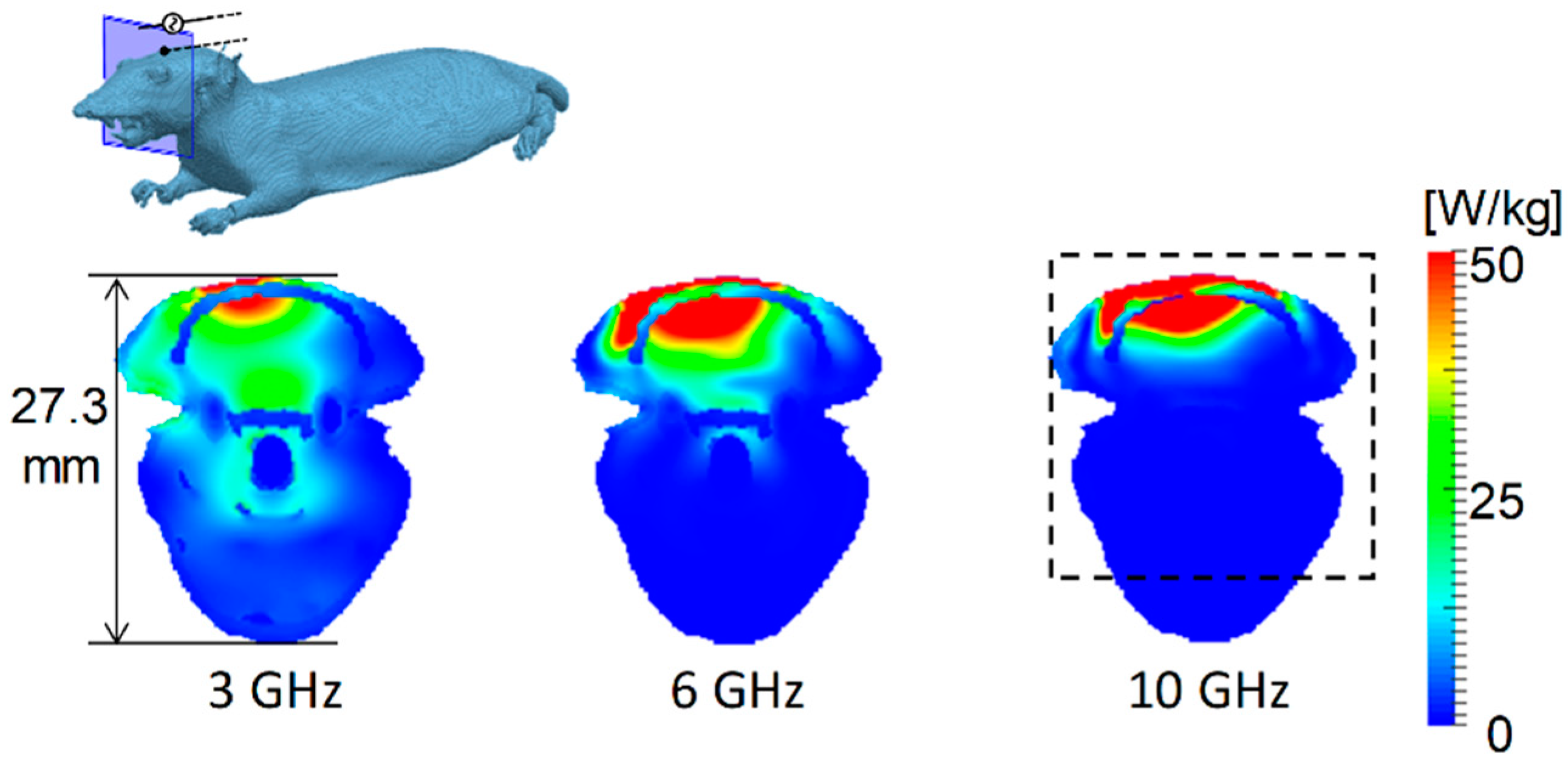
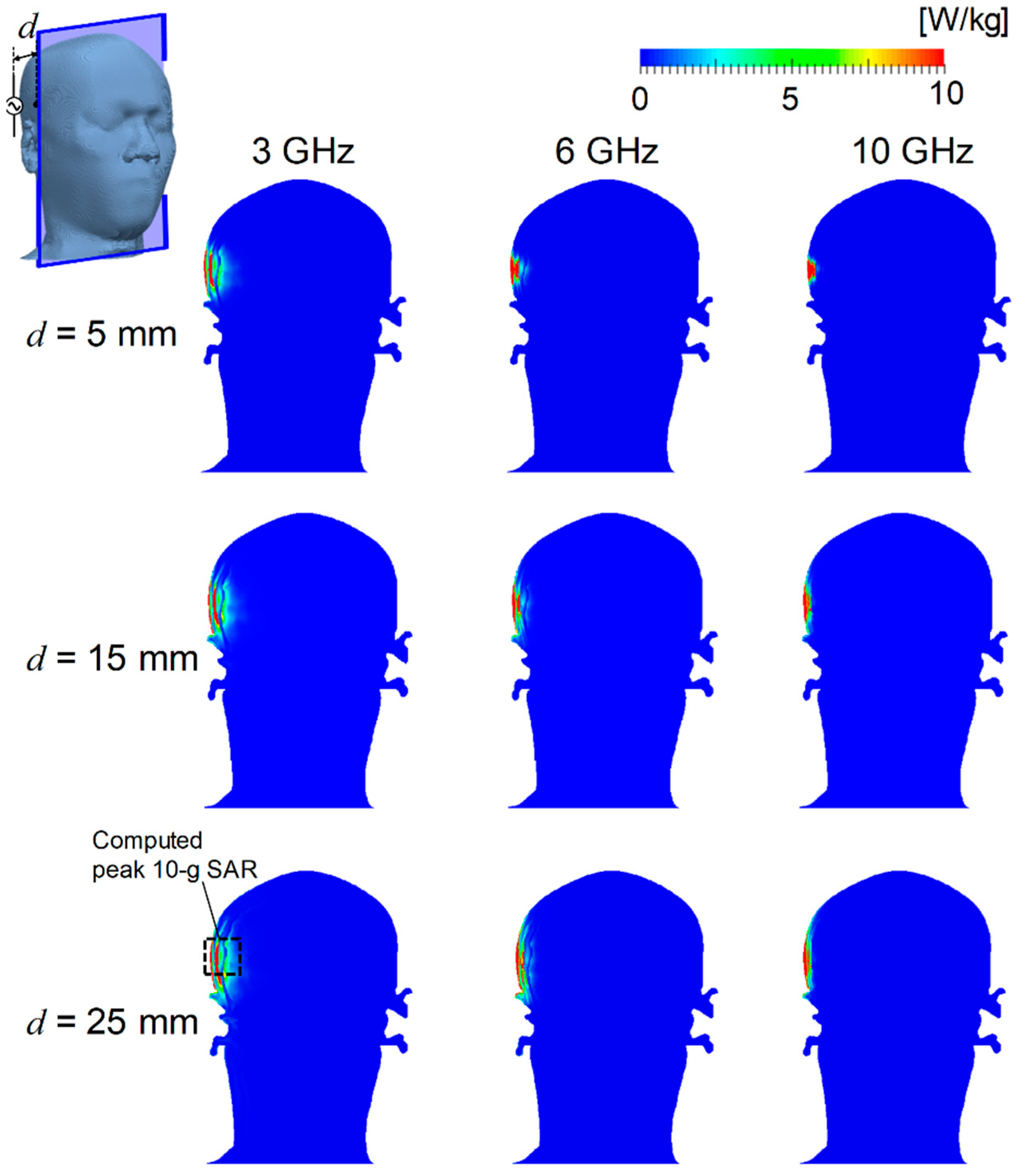
3.1. Distribution of SAR and Temperature Elevation
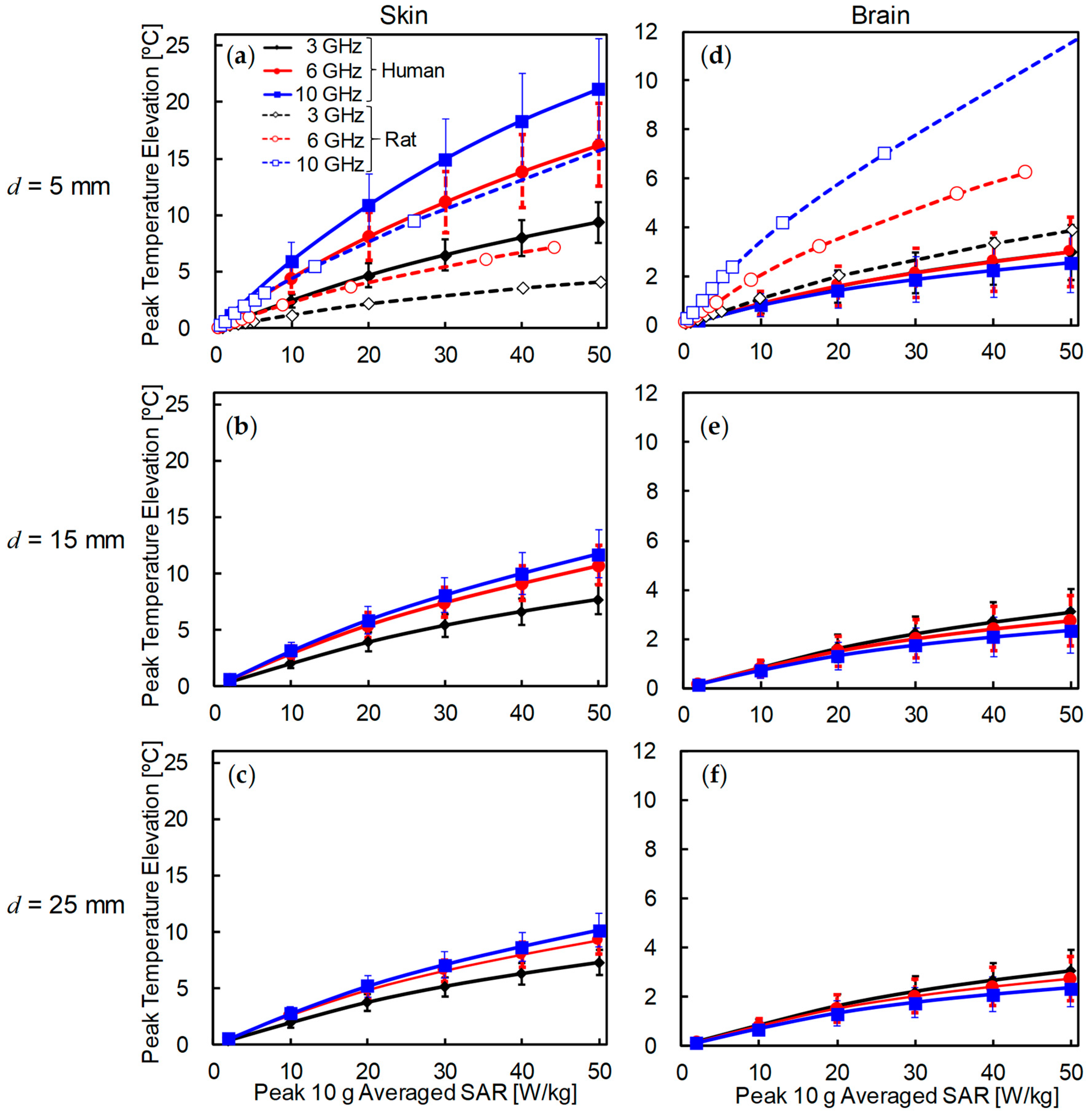
3.2. Comparison of Temperature Elevation in Rat and Human Models
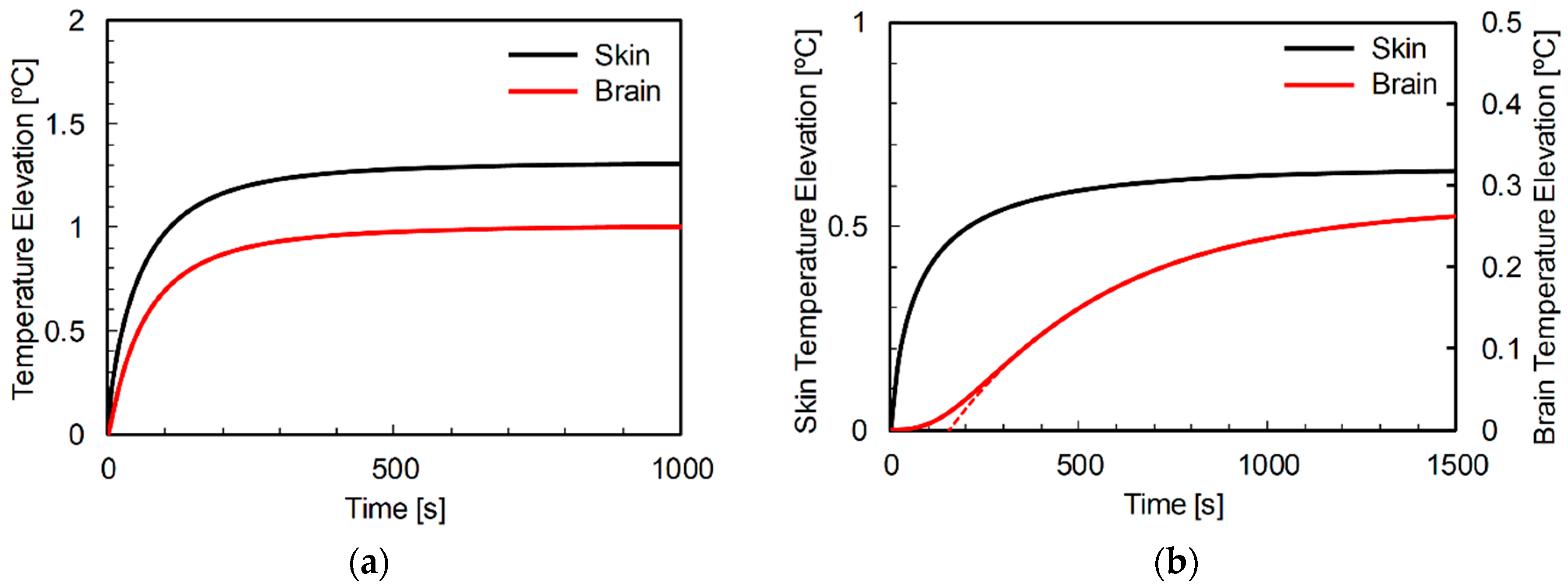
3.3. Thermal Time Constant in Rat and Human Head Models
3.4. Relationship between Effective SAR Volume and Thermal Time Constant
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Comment of Maximum SAR

References
- Ahlbom, A.; Bergqvist, U.; Bernhardt, J.H.; Cesarini, J.P.; Grandolfo, M.; Hietanen, M.; Mckinlay, A.F.; Repacholi, M.H.; Sliney, D.H.; Stolwijk, J.A.; et al. Guidelines for limiting exposure to time-varying electric, magnetic, and electromagnetic fields (up to 300 GHz). Health Phys. 1998, 75, 494–522. [Google Scholar] [CrossRef]
- IEEE C95.1. IEEE Standard for Safety Levels with Respect to Human Exposure to Radio Frequency Electromagnetic Fields, 3 kHz to 300 GHz; IEEE Std C95.1-2005; IEEE: Piscataway, NJ, USA, 2006. [Google Scholar] [CrossRef]
- Chou, C.-K.; Guy, A.W.; Kunz, L.L.; Johnson, R.B.; Crowley, J.J.; Krupp, J.H. Long-term, low-level microwave irradiation of rats. Bioelectromagnetics 1992, 13, 469–496. [Google Scholar] [CrossRef] [PubMed]
- Kojima, M.; Hata, I.; Wake, K.; Watanabe, S.I.; Yamanaka, Y.; Kamimura, Y.; Taki, M.; Sasaki, K. Influence of anesthesia on ocular effects and temperature in rabbit eyes exposed to microwaves. Bioelectromagnetics 2004, 25, 228–233. [Google Scholar] [CrossRef] [PubMed]
- ICNIRP 16/2009 ICNIRP_Review: Exposure to High Frequency Electromagnetic Fields, Biological Effects and Health Consequences (100 kHz–300 GHz) 2012. Available online: https://www.icnirp.org/en/publications/article/hf-review-2009.html (accessed on 22 June 2018).
- Hirata, A.; Sugiyama, H.; Kojima, M.; Kawai, H.; Yamashiro, Y.; Fujiwara, O.; Watanabe, S.; Sasaki, K. Computational model for calculating body-core temperature elevation in rabbits due to whole-body exposure at 2.45 GHz. Phys. Med. Biol. 2008, 53, 3391–3404. [Google Scholar] [CrossRef] [PubMed]
- Hirata, A.; Masuda, H.; Kanai, Y.; Asai, R.; Fujiwara, O.; Arima, T.; Kawai, H.; Watanabe, S.; Lagroye, I.; Veyret, B. Computational modeling of temperature elevation and thermoregulatory response in the brains of anesthetized rats locally exposed at 1.5 GHz. Phys. Med. Biol. 2011, 56, 7639–7657. [Google Scholar] [CrossRef] [PubMed]
- Bernardi, P.; Cavagnaro, M.; Pisa, S.; Piuzzi, E. Specific absorption rate and temperature elevation in a subject exposed in the far-field of radio-frequency sources operating in the 10–900-MHz range. IEEE Trans. Biomed. Eng. 2003, 50, 295–304. [Google Scholar] [CrossRef] [PubMed]
- Hirata, A.; Asano, T.; Fujiwara, O. FDTD analysis of body-core temperature elevation in children and adults for whole-body exposure. Phys. Med. Biol. 2008, 53, 5223–5238. [Google Scholar] [CrossRef] [PubMed]
- Nelson, D.A.; Charbonnel, S.; Curran, A.R.; Marttila, E.A.; Fiala, D.; Mason, P.A.; Ziriax, J.M. A high-resolution voxel model for predicting local tissue temperatures in humans subjected to warm and hot environments. J. Biomech. Eng. 2009, 131, 041003. [Google Scholar] [CrossRef] [PubMed]
- Moore, S.M.; McIntosh, R.L.; Iskra, S.; Wood, A.W. Modeling the effect of adverse environmental conditions and clothing on temperature rise in a human body exposed to radio frequency electromagnetic fields. IEEE Trans. Biomed. Eng. 2015, 62, 627–637. [Google Scholar] [CrossRef] [PubMed]
- Foster, K.R.; Lozano-Nieto, A.; Riu, P.J.; Ely, T.S. Heating of tissues by microwaves: A model analysis. Bioelectromagnetics 1998, 19, 420–428. [Google Scholar] [CrossRef]
- Guy, A.W.; Lin, J.C.; Kramar, P.O.; Emery, A.F. Effect of 2450-MHz radiation on the rabbit eye. IEEE Trans. Microw. Theory Tech. 1975, 23, 492–498. [Google Scholar] [CrossRef]
- Kramár, P.; Harris, C.; Guy, A.W. Thermal cataract formation in rabbits. Bioelectromagnetics 1987, 8, 397–406. [Google Scholar] [CrossRef] [PubMed]
- Kuribayashi, M.; Wang, J.; Fujiwara, O.; Doi, Y.; Nabae, K.; Tamano, S.; Ogiso, T.; Asamoto, M.; Shirai, T. Lack of effects of 1439 MHz electromagnetic near field exposure on the blood-brain barrier in immature and young rats. Bioelectromagnetics 2005, 26, 578–588. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.; Hadjem, A.; Wong, M.F.; Gati, A.; Picon, O.; Wiart, J. Whole-body new-born and young rats’ exposure assessment in a reverberating chamber operating at 2.4 GHz. Phys. Med. Biol. 2010, 55, 1619–1630. [Google Scholar] [CrossRef] [PubMed]
- Masuda, H.; Hirota, S.; Ushiyama, A.; Hirata, A.; Arima, T.; Watanabe, H.; Wake, K.; Watanabe, S.; Taki, M.; Nagai, A.; et al. No changes in cerebral microcirculatory parameters in rat during local cortex exposure to microwaves. In Vivo 2015, 29, 207–215. [Google Scholar] [PubMed]
- Goldstein, L.S.; Dewhirst, M.W.; Repacholi, M.; Kheifets, L. Summary, conclusions and recommendations: Adverse temperature levels in the human body. Int. J. Hyperth. 2003, 19, 373–384. [Google Scholar] [CrossRef] [PubMed]
- Sienkiewicz, Z.; Van Rongen, E.; Croft, R.; Ziegelberger, G.; Veyret, B. ICNIRP Statement: A closer look at the thresholds of thermal damage: Workshop report by an ICNIRP task group. Health Phys. 2016, 111, 300–306. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Fujiwara, O. FDTD computation of temperature rise in the human head for portable telephones. IEEE Trans. Microw. Theory Tech. 1999, 47, 1528–1534. [Google Scholar] [CrossRef]
- Bernardi, P.; Cavagnaro, M.; Pisa, S.; Piuzzi, E. Specific absorption rate and temperature increases in the head of a cellular-phone user. IEEE Trans. Microw. Theory Tech. 2000, 48, 1118–1126. [Google Scholar] [CrossRef]
- Leeuwen, V.; Lagendijk, J.J.W.; Leersum, V.; Zwamborn, A.P.M.; Hornsleth, S.N.; Kotte, A.N.T.J. Calculation of change in brain temperatures due to exposure to a mobile phone. Phys. Med. Biol. 1999, 44, 2367–2379. [Google Scholar] [CrossRef] [PubMed]
- Morimoto, R.; Hirata, A.; Laakso, I.; Ziskin, M.C.; Foster, K.R. Time constants for temperature elevation in human models exposed to dipole antennas and beams in the frequency range from 1 to 30 GHz. Phys. Med. Biol. 2017, 62, 1676–1699. [Google Scholar] [CrossRef] [PubMed]
- Van Rhoon, G.C.; Samaras, T.; Yarmolenko, P.S.; Dewhirst, M.W.; Neufeld, E.; Kuster, N. CEM43 °C thermal dose thresholds: A potential guide for magnetic resonance radiofrequency exposure levels? Eur. Radiol. 2013, 23, 2215–2227. [Google Scholar] [CrossRef] [PubMed]
- Kodera, S.; Gomez-Tames, J.; Hirata, A.; Masuda, H.; Arima, T.; Watanabe, S. Multiphysics and thermal response models to improve accuracy of local temperature estimation in rat cortex under microwave exposure. Int. J. Environ. Res. Public Health 2017, 14, 358. [Google Scholar] [CrossRef] [PubMed]
- Wake, K.; Hongo, H.; Watanabe, S.; Taki, M.; Kamimura, Y.; Yamanaka, Y.; Uno, T.; Member, S.; Kojima, M. Development of a 2.45-GHz local exposure system for in vivo study on ocular effects. IEEE Trans. Microw. Theory Tech. 2007, 55, 588–596. [Google Scholar] [CrossRef]
- Nagaoka, T.; Watanabe, S.; Sakurai, K.; Kunieda, E.; Watanabe, S.; Taki, M.; Yamanaka, Y. Development of realistic high-resolution whole-body voxel models of Japanese adult males and females of average height and weight, and application of models to radio-frequency electromagnetic-field dosimetry. Phys. Med. Biol. 2004, 49, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Christ, A.; Kainz, W.; Hahn, E.G.; Honegger, K.; Zefferer, M.; Neufeld, E.; Rascher, W.; Janka, R.; Bautz, W.; Chen, J.; et al. The Virtual Family—Development of surface-based anatomical models of two adults and two children for dosimetric simulations. Phys. Med. Biol. 2010, 55. [Google Scholar] [CrossRef] [PubMed]
- Kodera, S.; Gomez-Tames, J.; Hirata, A. Temperature elevation in the human brain and skin with thermoregulation during exposure to RF energy. Biomed. Eng. Online 2018, 17, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Taflove, A.; Hagness, S.C. Computational Electrodynamics: The Finite-Difference Time-Domain Method, 3rd ed.; Artech House: Norwood, MA, USA, 2005; ISBN 1580538320/9781580538329. [Google Scholar]
- Roden, J.A.; Gedney, S.D. Convolutional PML(CPML): An efficient FDTD implementation of the CFS-PML for arbitrary media. Microw. Opt. Technol. Lett. 2000, 27, 334–339. [Google Scholar] [CrossRef]
- Gabriel, C. Compilation of the Dielectric Properties of Body Tissues at RF and Microwave Frequencies, 1st ed.; King’s College London: London, UK, 1996. [Google Scholar]
- Sasaki, K.; Wake, K.; Watanabe, S. Development of best fit Cole-Cole parameters for measurement data from biological tissues and organs between 1 MHz and 20 GHz. Radio Sci. 2014, 49, 459–472. [Google Scholar] [CrossRef] [Green Version]
- IEEE C95.3. IEEE Recommended Practice for Measurements and Computations of Radio Frequency Electromagnetic Fields with Respect to Human Exposure to Such Fields, 100 kHz–300 GHz; Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA, 2002; ISBN 9780738135205. [Google Scholar]
- Pennes, H.H. Analysis of tissue and arterial blood temperatures in the resting human forearm. J. Appl. Physiol. 1948, 1, 93–122. [Google Scholar] [CrossRef] [PubMed]
- Oizumi, T.; Laakso, I.; Hirata, A.; Fujiwara, O.; Watanabe, S.; Taki, M.; Kojima, M.; Sasaki, H.; Sasaki, K. FDTD analysis of temperature elevation in the lens of human and rabbit models due to near-field and far-field exposures at 2.45 GHz. Radiat. Prot. Dosimetry 2013, 155, 284–291. [Google Scholar] [CrossRef] [PubMed]
- Hirata, A.; Asano, T.; Fujiwara, O. FDTD analysis of human body-core temperature elevation due to RF far-field energy prescribed in the ICNIRP guidelines. Phys. Med. Biol. 2007, 52, 5013–5023. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.B.; Blaufox, M.D. Blood volume in the rat. J. Nucl. Med. 1985, 26, 72–76. [Google Scholar] [PubMed]
- Stolwijk, J.A. A mathematical model of physiological temperature regulation in man. NASA Contract. Rep. 1971, CR-1855, 77. [Google Scholar]
- Hirata, A.; Fujiwara, O. Modeling time variation of blood temperature in a bioheat equation and its application to temperature analysis due to RF exposure. Phys. Med. Biol. 2009, 54, N189–N196. [Google Scholar] [CrossRef] [PubMed]
- Hoque, M.; Gandhi, O.P. Temperature distributions in the human leg for VLF-VHF exposures at the ANSI-recommended safety levels. IEEE Trans. Biomed. Eng. 1988, 35, 442–449. [Google Scholar] [CrossRef] [PubMed]
- Chatterjee, I.; Gandhi, O.P. An inhomogeneous thermal block model of man for the electromagnetic environment. IEEE Trans. Biomed. Eng. 1983, 30, 707–715. [Google Scholar] [CrossRef] [PubMed]
- Hirata, A.; Fujiwara, O.; Shiozawa, T. Correlation between peak spatial-average SAR and temperature increase due to antennas attached to human trunk. IEEE Trans. Biomed. Eng. 2006, 53, 1658–1664. [Google Scholar] [CrossRef] [PubMed]
- Fiala, D.; Lomas, K.J.; Stohrer, M. A computer model of human thermoregulation for a wide range of environmental conditions:the passive system. J. Appl. Physiol. Publ. 1999, 87, 1957–1972. [Google Scholar] [CrossRef] [PubMed]
- Hirata, A.; Watanabe, S.; Fujiwara, O.; Kojima, M.; Sasaki, K.; Shiozawa, T. Temperature elevation in the eye of anatomically based human head models for plane-wave exposures. Phys. Med. Biol. 2007, 52, 6389–6399. [Google Scholar] [CrossRef] [PubMed]
- Fiala, D.; Lomas, K.; Stohrer, M. Computer prediction of human thermoregulatory and temperature responses to a wide range of environmental conditions. Int. J. Biometeorol. 2001, 45, 143–159. [Google Scholar] [CrossRef] [PubMed]
- Laakso, I.; Hirata, A. Dominant factors affecting temperature rise in simulations of human thermoregulation during RF exposure. Phys. Med. Biol. 2011, 56, 7449–7471. [Google Scholar] [CrossRef] [PubMed]
- ICNIRP Draft Appendix A: Guidelines for limiting exposure to time-varying electric, magnetic, and electromagnetic fields (up to 300 GHz). Health Phys. 2018, 74, 494–521.
- Foster, K.R.; Ziskin, M.C.; Balzano, Q. Thermal response of human skin to microwave energy: A critical review. Health Phys. 2016, 111, 528–541. [Google Scholar] [CrossRef] [PubMed]
- Hirata, A.; Fujimoto, M.; Asano, T.; Wang, J.; Fujiwara, O.; Shiozawa, T. Correlation between maximum temperature increase and peak SAR with different average schemes and masses. IEEE Trans. Electromagn. Compat. 2006, 48, 569–578. [Google Scholar] [CrossRef]
- Hashimoto, Y.; Hirata, A.; Morimoto, R.; Aonuma, S.; Laakso, I.; Jokela, K.; Foster, K. On the averaging area for incident power density for human exposure limits at frequencies over 6 GHz. Phys. Med. Biol. 2017, 62, 3124–3138. [Google Scholar] [CrossRef] [PubMed]
- Dielectric Properties of Body Tissues. Available online: http://niremf.ifac.cnr.it/tissprop/htmlclie/htmlclie.php (accessed on 22 June 2018).
- Lee, A.K.; Choi, H.D.; Lee, H.S.; Pack, J.K. Human head size and SAR characteristics for handset exposure. ETRI J. 2002, 24, 176–179. [Google Scholar] [CrossRef]
- Bit-Babik, G.; Guy, A.W.; Chou, C.-K.; Faraone, A.; Kanda, M.; Gessner, A.; Wang, J.; Fujiwara, O. Simulation of exposure and SAR estimation for adult and child heads exposed to radiofrequency energy from portable communication devices. Radiat. Res. 2005, 163, 580–590. [Google Scholar] [CrossRef] [PubMed]
- Hirata, A.; Watanabe, S.; Kojima, M.; Hata, I.; Wake, K.; Taki, M.; Sasaki, K.; Fujiwara, O.; Shiozawa, T. Computational verification of anesthesia effect on temperature variations in rabbit eyes exposed to 2.45 GHz microwave energy. Bioelectromagnetics 2006, 27, 602–612. [Google Scholar] [CrossRef] [PubMed]
- Hirata, A.; Kojima, M.; Kawai, H.; Yamashiro, Y.; Watanabe, S.; Sasaki, H.; Fujiwara, O. Acute dosimetry and estimation of threshold-inducing behavioral signs of thermal stress in rabbits at 2.45-GHz microwave exposure. IEEE Trans. Biomed. Eng. 2010, 57, 1234–1242. [Google Scholar] [CrossRef] [PubMed]
- Morimoto, R.; Laakso, I.; De Santis, V.; Hirata, A. Relationship between peak spatial-averaged specific absorption rate and peak temperature elevation in human head in frequency range of 1–30 GHz. Phys. Med. Biol. 2016, 61, 5406–5425. [Google Scholar] [CrossRef] [PubMed]
- National Toxicology Program Technical Report on the Toxicology and Carcinogenesis Studies in Hsd:Sprague Dawley SD Rats Exposed to Whole-Body Radio Frequency Radiation at a Frequency (900 MHz) and Modulations (GSM and CDMA) Used by Cell Phones. 2018, NTP TR 595. Available online: https://www.emfdata.org/de/studien/detail&id=440 (accessed on 22 June 2018).
- National Toxicology Program Technical Report on the Toxicology and Carcinogenesis Studies in B6C3F1/N Mice Exposed to Whole-Body Radio Frequency Radiation at a Frequency (1900 MHz) and Modulations (GSM and CDMA) Used by Cell Phones. 2018, NTP TR 596. Available online: https://ntp.niehs.nih.gov/ntp/about_ntp/trpanel/2018/march/tr596peerdraft.pdf (accessed on 22 June 2018).
- ICNIRP Note: ICNIRP Note on Recent Animal Carcinogenesis Studies. Available online: https://www.icnirp.org/cms/upload/publications/ICNIRPnote2018.pdf (accessed on 22 June 2018).
- Reilly, J.P.; Hirata, A. Low-frequency electrical dosimetry: Research agenda of the IEEE International Committee on Electromagnetic Safety. Phys. Med. Biol. 2016, 61, R138–R149. [Google Scholar] [CrossRef] [PubMed]
- Gomez-Tames, J.; Laakso, I.; Haba, Y.; Hirata, A.; Poljak, D.; Yamazaki, K. Computational artifacts of the in situ electric field in Anatomical Models Exposed to Low-Frequency Magnetic Field. IEEE Trans. Electromagn. Compat. 2018, 60, 589–597. [Google Scholar] [CrossRef]



© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kodera, S.; Hirata, A. Comparison of Thermal Response for RF Exposure in Human and Rat Models. Int. J. Environ. Res. Public Health 2018, 15, 2320. https://0-doi-org.brum.beds.ac.uk/10.3390/ijerph15102320
Kodera S, Hirata A. Comparison of Thermal Response for RF Exposure in Human and Rat Models. International Journal of Environmental Research and Public Health. 2018; 15(10):2320. https://0-doi-org.brum.beds.ac.uk/10.3390/ijerph15102320
Chicago/Turabian StyleKodera, Sachiko, and Akimasa Hirata. 2018. "Comparison of Thermal Response for RF Exposure in Human and Rat Models" International Journal of Environmental Research and Public Health 15, no. 10: 2320. https://0-doi-org.brum.beds.ac.uk/10.3390/ijerph15102320




