Quantitative Assessment of Relationship between Population Exposure to PM2.5 and Socio-Economic Factors at Multiple Spatial Scales over Mainland China
Abstract
:1. Introduction
2. Data and Methods
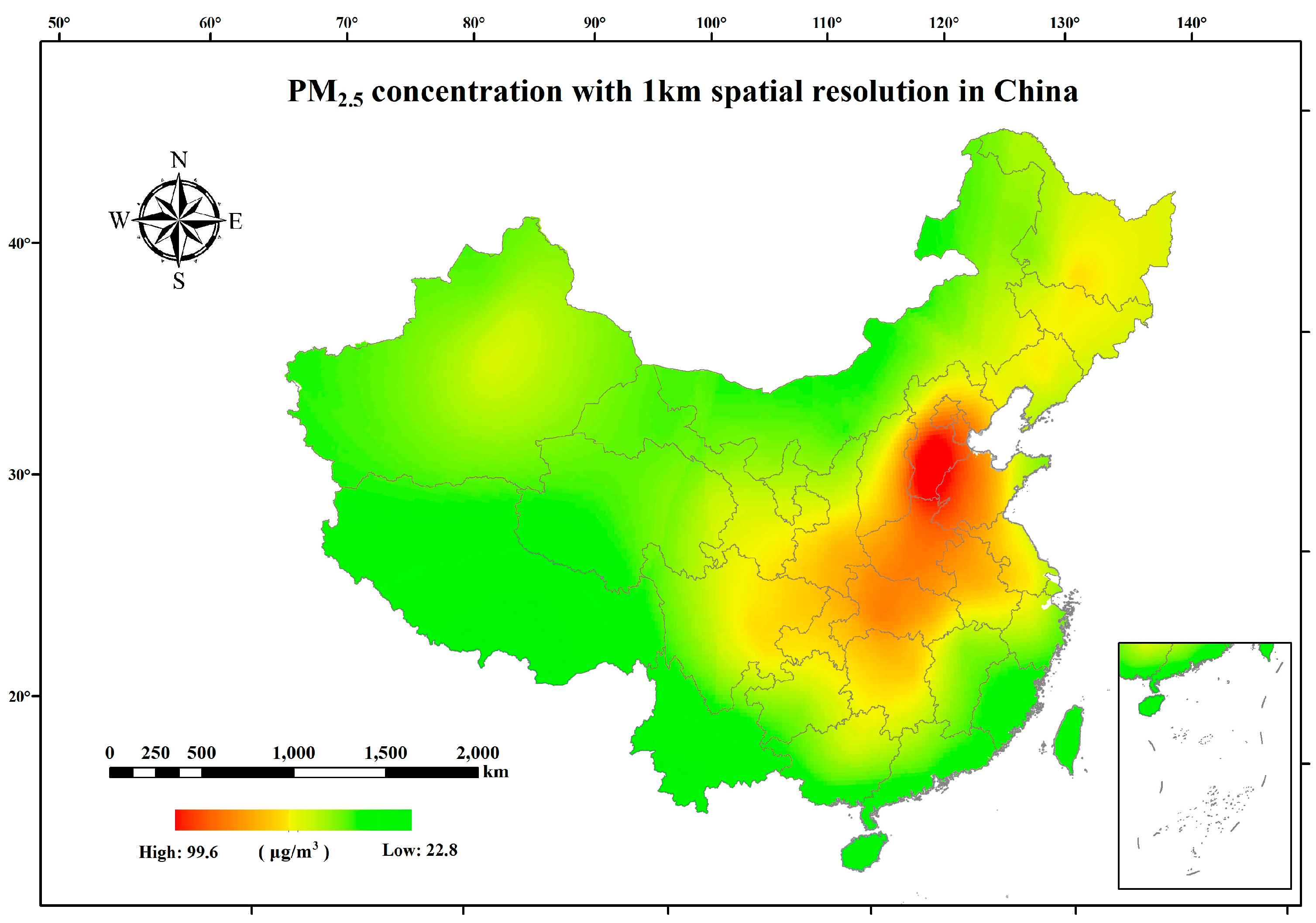
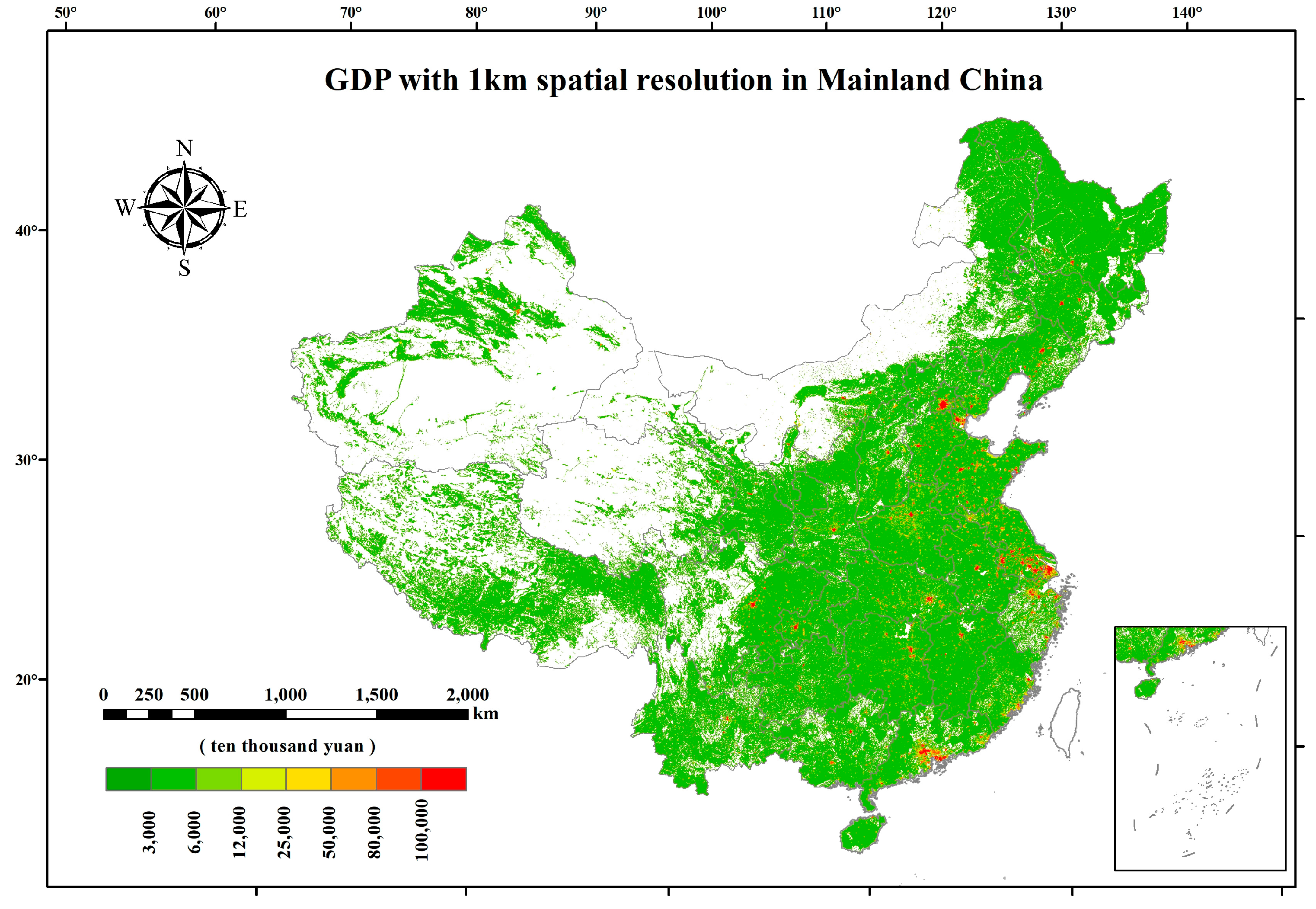
2.1. Datasets
2.2. Population Exposure Calculation
2.3. Spatial Correlation Analysis
2.4. Quantile Regression Method
3. Results and Discussion
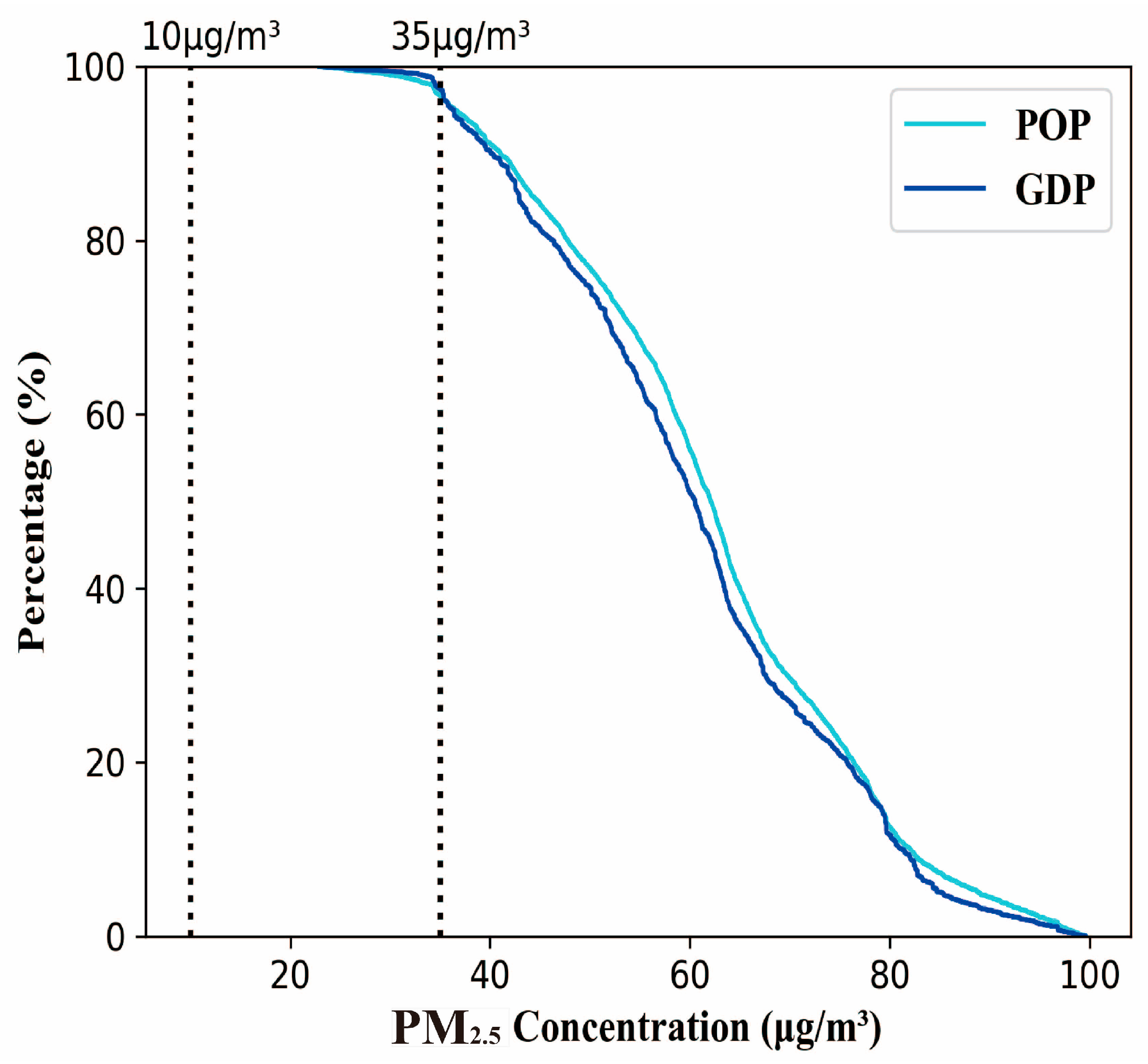
3.1. Population Exposure and Economic Effects on PM2.5
3.2. Spatial Correlation between PM2.5 and Socio-Economic Factors
3.3. Quantile Regression Analysis of Economic Effects on PM2.5 Exposure
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Liang, Z.; Ma, M.; Du, G. Comparison of characteristics and trend analysis of atmospheric pollution in Beijing-Tainji-Shijiazhuang during 2003–2012. Environ. Eng. 2014, 12, 76–81. [Google Scholar]
- Kioumourtzoglou, M.A.; Schwartz, J.; James, P.; Dominici, F.; Zanobetti, A. PM2.5 and mortality in 207 US cities: Modification by temperature and city characteristics. Epidemiology 2016, 27, 221–227. [Google Scholar] [PubMed]
- Di, Q.; Wang, Y.; Zanobetti, A.; Wang, Y.; Koutrakis, P.; Choirat, C.; Dominici, F.; Schwartz, J.D. Air pollution and mortality in the medicare population. N. Engl. J. Med. 2017, 376, 2513–2522. [Google Scholar] [CrossRef] [PubMed]
- Franklin, B.A.; Brook, R.; Pope, C.A. Air pollution and cardiovascular disease. Curr. Probl. Cardiol. 2015, 40, 207–238. [Google Scholar] [CrossRef] [PubMed]
- Kaufman, J.D.; Adar, S.D.; Barr, R.G.; Budoff, M.; Burke, G.L.; Curl, C.L.; Daviqlus, M.L.; Diez Roux, A.V.; Gassett, A.J.; Jacobs, D.R., Jr.; et al. Association between air pollution and coronary artery calcification within six metropolitan areas in the USA (the multi-ethnic study of atherosclerosis and air pollution): A longitudinal cohort study. Lancet 2016, 388, 696–704. [Google Scholar] [CrossRef]
- Zhang, H.; Shi, C.; Wu, B.; Yang, Y. Quantified relationships among the visibility, relative humidity and PM2.5 mass concentration in Hefei city. Ecol. Environ. 2017, 26, 1001–1008. [Google Scholar]
- Gui, Z.; Zheng, Y.; Qian, Z.; He, H.; Zeng, X. Numerical study of indirect aerosols effect on regional climate over eastern China. J. Nanjing Univ. Nat. Sci. 2014, 50, 781–791. [Google Scholar]
- Lang, J.; Zhang, Y.; Zhou, Y.; Cheng, S.; Chen, D.; Guo, X.; Chen, S.; Li, X.; Xing, X.; Wang, H. Trends of PM2.5 and chemical composition in Beijing, 2000–2015. Aerosol Air Qual. Res. 2017, 17, 412–425. [Google Scholar] [CrossRef]
- Yao, L.; Lu, N.; Yue, X.; Du, J.; Yang, C. Comparison of hourly PM2.5 observations between urban and suburban areas in Beijing, China. Int. J. Environ. Res. Public Health 2015, 12, 12264–12276. [Google Scholar] [CrossRef] [PubMed]
- Song, C.; Pei, T.; Yao, L. Analysis of the characteristics and evolution modes of PM2.5 pollution episodes in Beijing, China during 2013. Int. J. Environ. Res. Public Health 2015, 12, 1099–1111. [Google Scholar] [CrossRef] [PubMed]
- Ye, B.; Ji, X.; Yang, H.; Yao, X.; Chan, C.K.; Cadle, S.H.; Chan, T.; Mulawa, P.A. Concentration and chemical composition of PM2.5 in Shanghai for a 1-year period. Atmos. Environ. 2003, 37, 499–510. [Google Scholar] [CrossRef]
- Shen, G.F.; Yuan, S.Y.; Xie, Y.N.; Xia, S.J.; Li, L.; Yao, Y.K.; Qiao, Y.Z.; Zhang, J.; Zhao, Q.Y.; Ding, A.J.; et al. Ambient levels and temporal variations of PM2.5 and PM10 at a residential site in the mega-city, Nanjing, in the western Yangtze River delta, China. J. Environ. Sci. Health Part A 2014, 49, 171–178. [Google Scholar] [CrossRef] [PubMed]
- Zhao, P.S.; Dong, F.; He, D.; Zhao, X.J.; Zhang, X.L.; Zhang, W.Z.; Yao, Q.; Liu, H.Y. Characteristics of concentrations and chemical compositions for PM2.5 in the region of Beijing, Tianjin, and Hebei, China. Atmos. Chem. Phys. 2013, 13, 4631–4644. [Google Scholar] [CrossRef]
- Yao, L. Causative impact of air pollution on evapotranspiration in the north china plain. Environ. Res. 2017, 158, 436–442. [Google Scholar] [CrossRef] [PubMed]
- Ming, L.; Jin, L.; Li, J.; Fu, P.; Yang, W.; Liu, D.; Zhang, G.; Wang, Z.; Li, X. PM2.5 in the Yangtze River delta, China: Chemical compositions, seasonal variations, and regional pollution events. Environ. Pollut. 2017, 223, 200–212. [Google Scholar] [CrossRef] [PubMed]
- Hagler, G.S.W.; Bergin, M.H.; Salmon, L.G.; Yu, J.Z.; Wan, E.C.H.; Zheng, M.; Zeng, L.M.; Kiang, C.S.; Zhang, Y.H.; Lau, A.K.H.; et al. Source areas and chemical composition of fine particulate matter in the Pearl River delta region of China. Atmos. Environ. 2006, 40, 3802–3815. [Google Scholar] [CrossRef]
- Tang, X.; Chen, X.; Tian, Y. Chemical composition and source apportionment of PM2.5—A case study from one year continuous sampling in the Chang-Zhu-Tan urban agglomeration. Atmos. Pollut. Res. 2017, 8, 885–899. [Google Scholar] [CrossRef]
- Yao, L.; Lu, N. Spatiotemporal distribution and short-term trends of particulate matter concentration over China, 2006–2010. Environ. Sci. Pollut. Res. 2014, 21, 9665–9675. [Google Scholar] [CrossRef] [PubMed]
- Ma, Z.; Hu, X.; Sayer, A.M.; Levy, R.; Zhang, Q.; Xue, Y. Satellite-based spatiotemporal trends in PM2.5 concentrations: China, 2004–2013. Environ. Health Perspect. 2016, 124, 184–192. [Google Scholar] [CrossRef] [PubMed]
- Leclerc, A.; Chastang, J.F.; Menvielle, G.; Luce, D. Socioeconomic inequalities in premature mortality in France: Have they widened in recent decades? Soc. Sci. Med. 2006, 62, 2035–2045. [Google Scholar] [CrossRef] [PubMed]
- Melchior, M.; Goldberg, M.; Krieger, N.; Kawachi, I.; Menvielle, G.; Zins, M.; Berkman, L.F. Occupational class, occupational mobility and cancer incidence among middle-aged men and women: A prospective study of the French GAZEL cohort*. Cancer Causes Control 2005, 16, 515–524. [Google Scholar] [CrossRef] [PubMed]
- Challier, B.; Viel, J.F. Relevance and validity of a new French composite index to measure poverty on a geographical level. Rev. Epidemiol. Santé Publique 2001, 49, 41–50. [Google Scholar] [PubMed]
- Havard, S.; Deguen, S.; Bodin, J.; Louis, K.; Laurent, O.; Bard, D. A small-area index of socioeconomic deprivation to capture health inequalities in France. Soc. Sci. Med. 2008, 67, 2007–2016. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lin, G.; Fu, J.; Jiang, D.; Hu, W.; Dong, D.; Huang, Y.; Zhao, M. Spatio-temporal variation of PM2.5 concentrations and their relationship with geographic and socioeconomic factors in China. Int. J. Environ. Res. Public Health 2014, 11, 173–186. [Google Scholar] [CrossRef] [PubMed]
- The Center for International Earth Science Information Network (CIESIN)/Columbia University. Available online: http://www.ciesin.org/ (accessed on 5 June 2018).
- Wang, G.; Gu, S.; Chen, J.; Wu, X.; Yu, J. Assessment of health and economic effects by PM2.5 pollution in Beijing: A combined exposure-response and computable general equilibrium analysis. Environ. Technol. 2016, 37, 3131–3138. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Yao, L. PM2.5, population exposure and economic effects in urban agglomerations of China using ground-based monitoring data. Int. J. Environ. Res. Public Health 2017, 14, 716. [Google Scholar] [CrossRef] [PubMed]
- Yao, L.; Lu, N. Particulate matter pollution and population exposure assessment over mainland China in 2010 with remote sensing. Int. J. Environ. Res. Public Health 2014, 11, 5241–5250. [Google Scholar] [CrossRef] [PubMed]
- Saib, M.S.; Caudeville, J.; Carre, F.; Ganry, O.; Trugeon, A.; Cicolella, A. Spatial relationship quantification between environmental, socioeconomic and health data at different geographic levels. Int. J. Environ. Res. Public Health 2014, 11, 3765–3786. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Fu, J.; Jiang, D.; Lin, G.; Dong, D.; Yan, X. Spatiotemporal distribution of U5MR and their relationship with geographic and socioeconomic factors in China. Int. J. Environ. Res. Public Health 2017, 14, 1428. [Google Scholar] [CrossRef] [PubMed]
- The China National Environmental Monitoring Center (CNEMC). Available online: http://113.108.142.147:20035/emcpublish/ (accessed on 5 June 2018).
- Barry, N. The Chinese Economy: Transitions and Growth; The MIT Press: London, UK, 2007; pp. 18–19. [Google Scholar]
- Hao, Y.; Helen, F.; Monti, M.M.; Qualters, J.R. U.S. census unit population exposures to ambient air pollutants. Int. J. Health Geogr. 2012, 11, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Yu, K.; Lu, Z.; Stander, J. Quantile regression: Applications and current research areas. J. R. Stat. Soc. 2003, 52, 331–350. [Google Scholar] [CrossRef]
- Koenker, R.; Bassett, G. Regression quantiles. Econometrica 1978, 46, 33–50. [Google Scholar] [CrossRef]
- Van, A.D.; Martin, R.V.; Brauer, M.; Boys, B.L. Use of satellite observations for long-term exposure assessment of global concentrations of fine particulate matter. Environ. Health Perspect. 2015, 123, 135–143. [Google Scholar]



| Variable | PM2.5 | Population | GDP | Population Exposure |
|---|---|---|---|---|
| PM2.5 | - | 0.07 * | 0.18 * | 0.3 * |
| Population | 0.07 * | - | 0.73 * | 0.66 * |
| GDP | 0.19 * | 0.74 * | - | 0.88 * |
| Population Exposure | 0.3 * | 0.66 * | 0.88 * | - |
| Statistic | Quantile | |||
|---|---|---|---|---|
| 80% | 85% | 90% | 95% | |
| Grid (2,759,981 samples) | ||||
| GDP (10 thousand yuan) | 585.89 | 906.79 | 1678.91 | 5246.21 |
| Trend (person km−2 10 thousand yuan−1) | 0.87 * | 1.05 * | 1.31 * | 1.88 * |
| Std. Error | 0.005 | 0.0076 | 0.009 | 0.018 |
| p | <0.001 | <0.001 | <0.001 | <0.001 |
| County (2375 samples) | ||||
| GDP (10 thousand yuan) | 3,356,513.64 | 4,397,744.36 | 6,241,262.98 | 9,844,463.44 |
| Trend (person km−2 10 thousand yuan−1) | 1.16 * | 1.33 * | 1.47 * | 2.15 * |
| Std. Error | 0.125 | 0.173 | 0.22 | 0.71 |
| p | <0.001 | <0.001 | <0.001 | 0.003 |
| City (349 samples) | ||||
| GDP (10 thousand yuan) | 26,716,747.01 | 32,623,702.94 | 46,608,724.75 | 69,396,042.94 |
| Trend (person km−2 10 thousand yuan−1) | 0.022 | 0.012 | 0.001 | 0.124 |
| Std. Error | 0.018 | 0.017 | 0.12 | 0.275 |
| p | 0.225 | 0.48 | 0.99 | 0.65 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, L.; Huang, C.; Jing, W.; Yue, X.; Xu, Y. Quantitative Assessment of Relationship between Population Exposure to PM2.5 and Socio-Economic Factors at Multiple Spatial Scales over Mainland China. Int. J. Environ. Res. Public Health 2018, 15, 2058. https://0-doi-org.brum.beds.ac.uk/10.3390/ijerph15092058
Yao L, Huang C, Jing W, Yue X, Xu Y. Quantitative Assessment of Relationship between Population Exposure to PM2.5 and Socio-Economic Factors at Multiple Spatial Scales over Mainland China. International Journal of Environmental Research and Public Health. 2018; 15(9):2058. https://0-doi-org.brum.beds.ac.uk/10.3390/ijerph15092058
Chicago/Turabian StyleYao, Ling, Changchun Huang, Wenlong Jing, Xiafang Yue, and Yuyue Xu. 2018. "Quantitative Assessment of Relationship between Population Exposure to PM2.5 and Socio-Economic Factors at Multiple Spatial Scales over Mainland China" International Journal of Environmental Research and Public Health 15, no. 9: 2058. https://0-doi-org.brum.beds.ac.uk/10.3390/ijerph15092058





