Risk Assessment of An Earthquake-Collapse-Landslide Disaster Chain by Bayesian Network and Newmark Models
Abstract
:1. Introduction
2. Methods and Materials
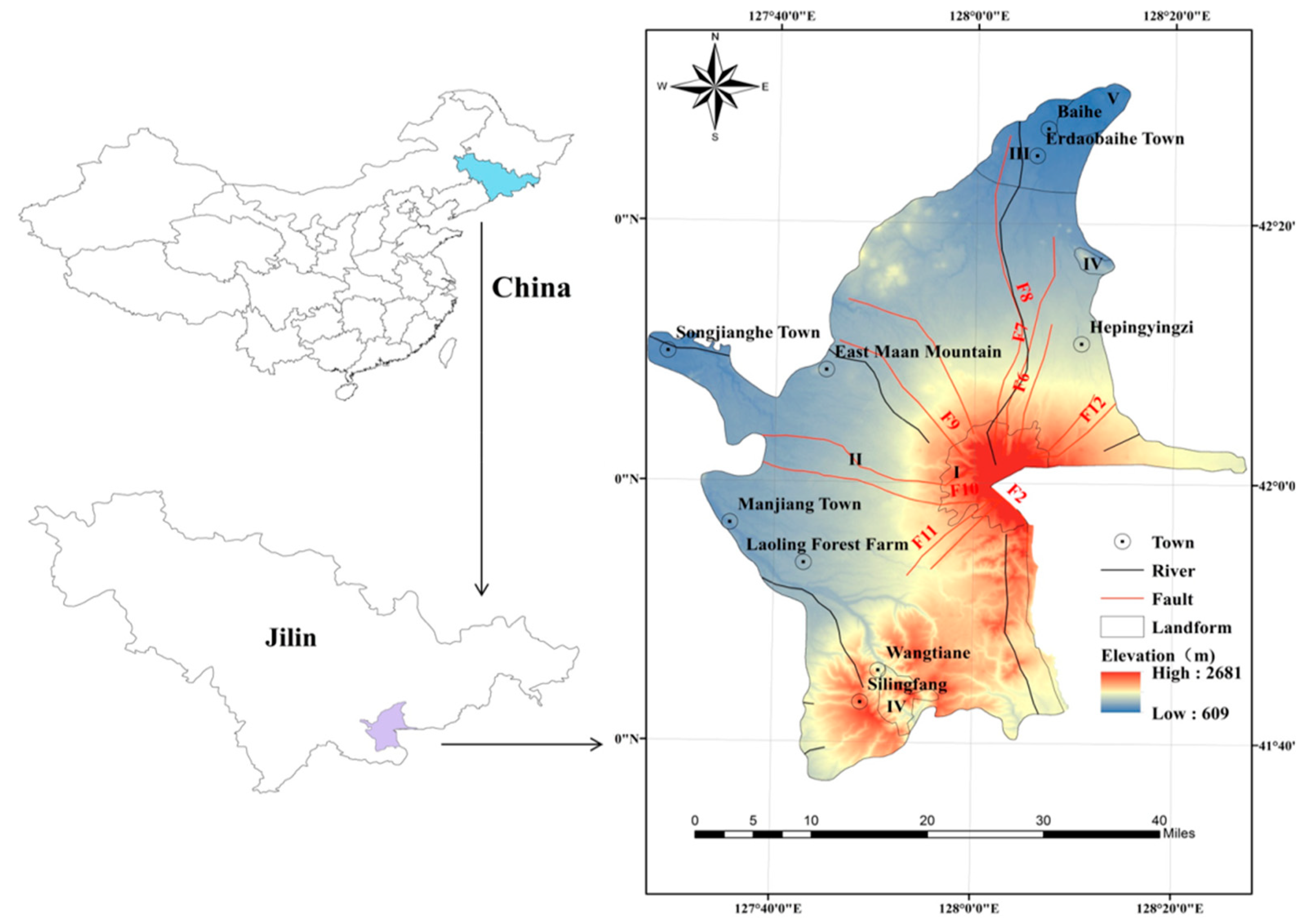
2.1. The Study Area
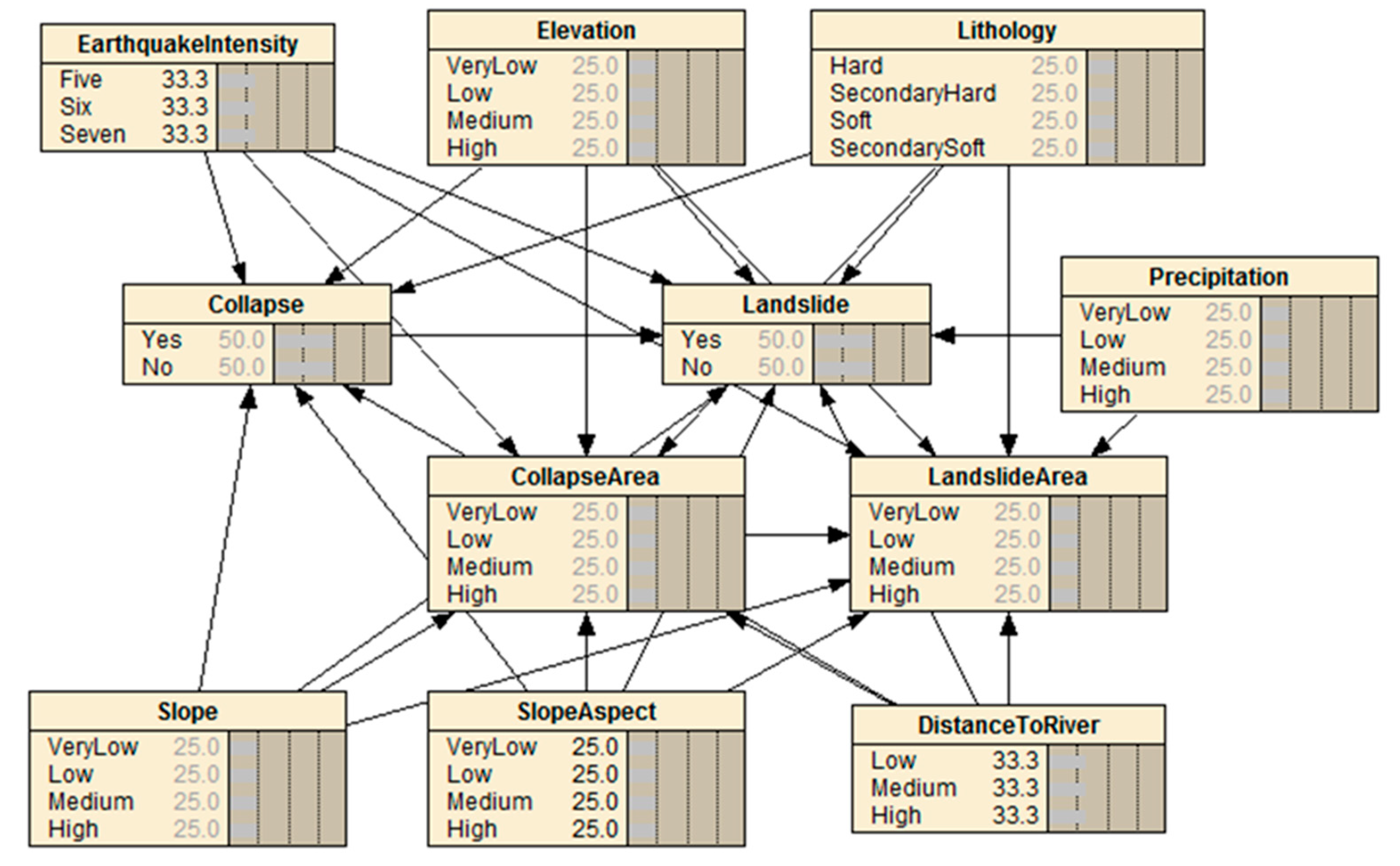
2.2. Bayesian Network Model
2.3. Newmark Model
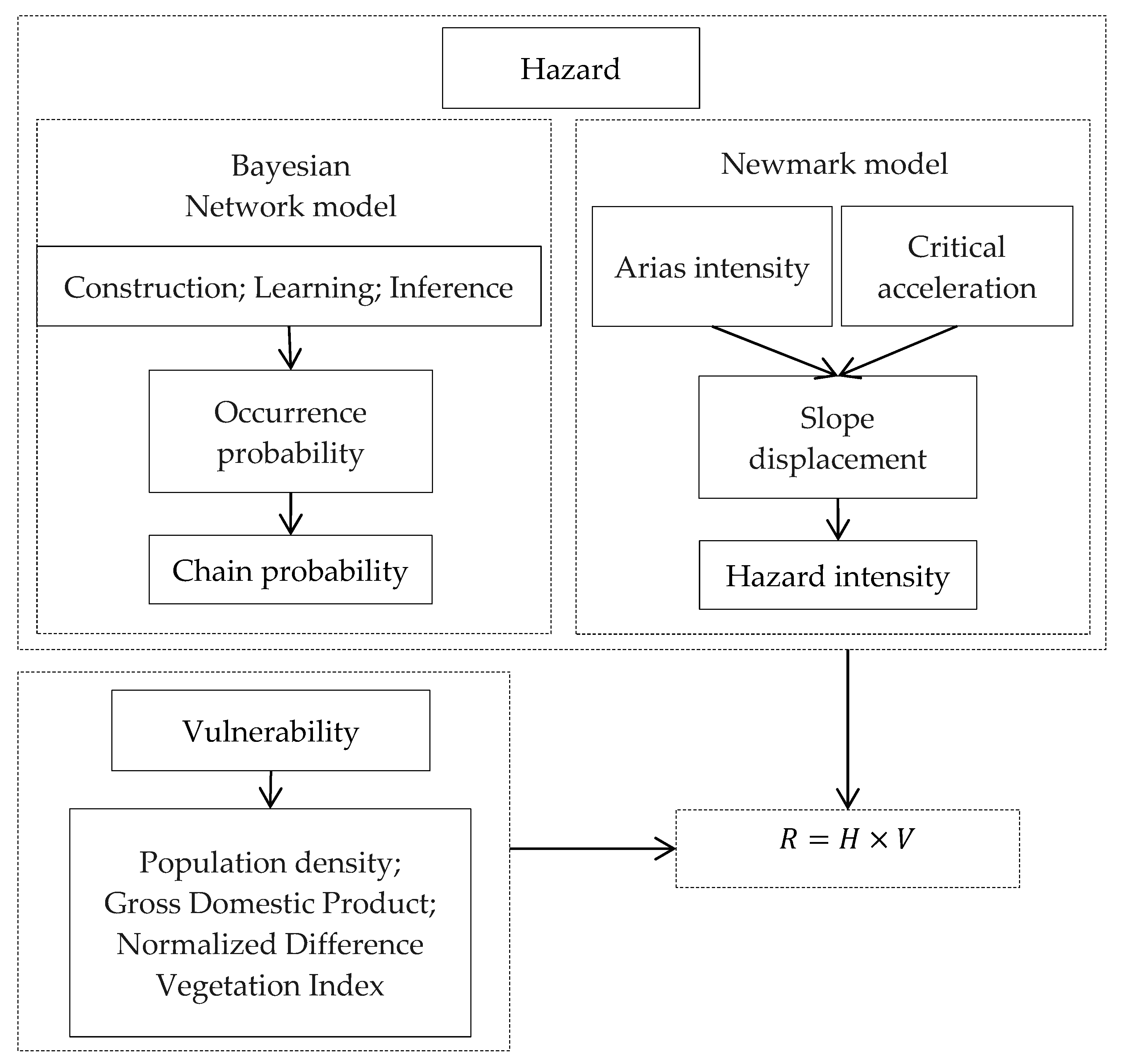
2.4. Earthquake Disaster Chain Risk Assessment Model
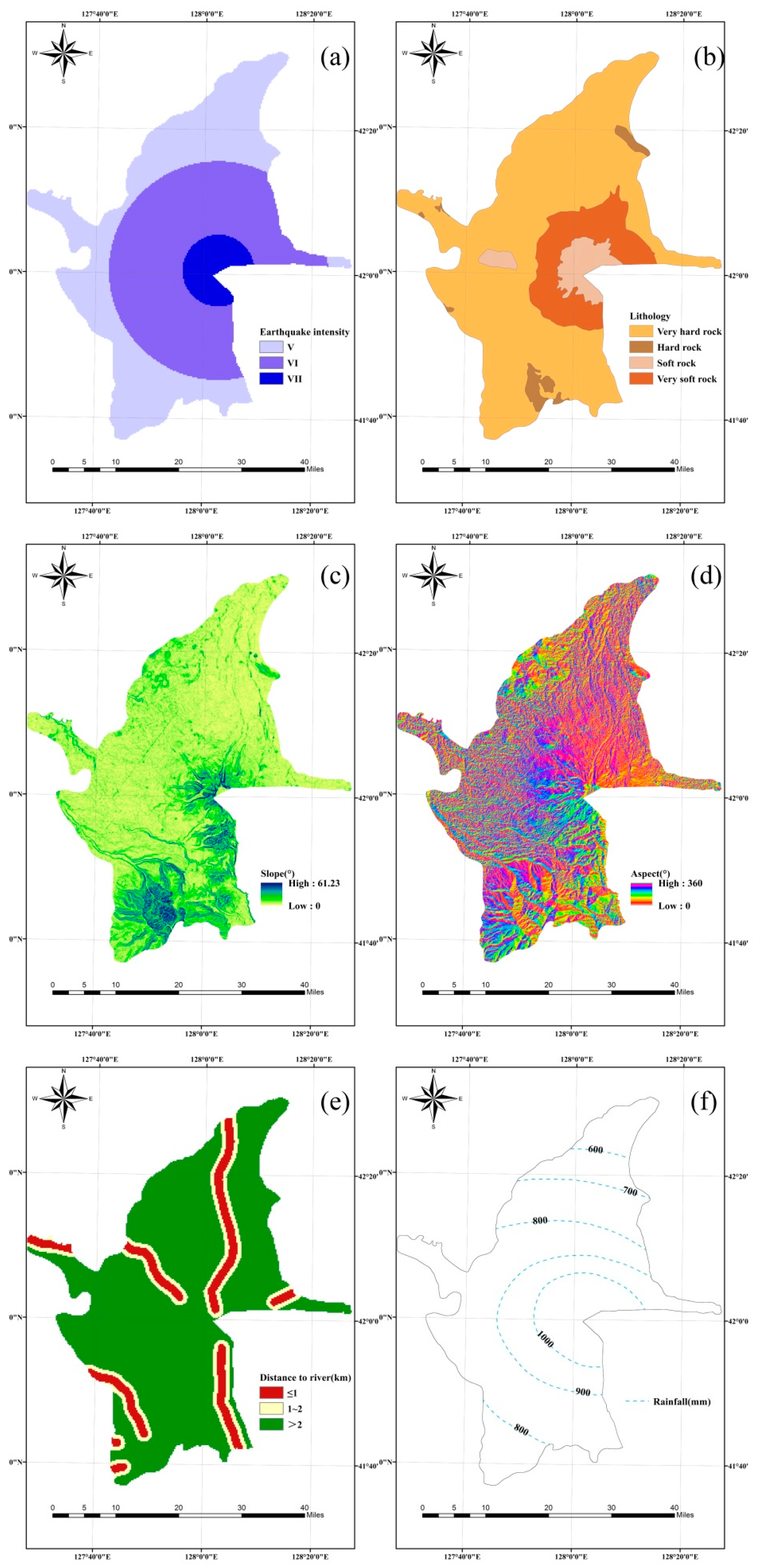
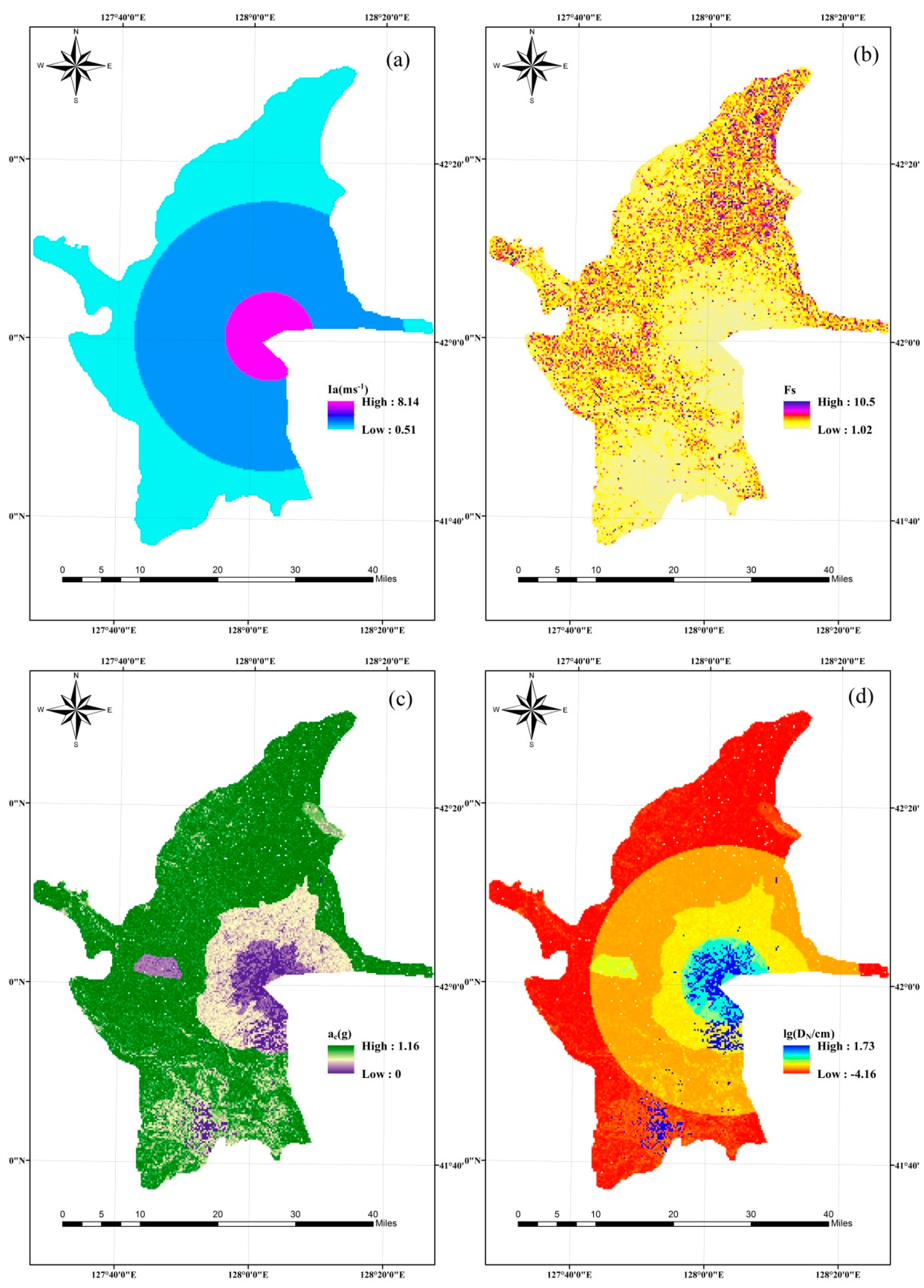
2.5. Data and Model Parameters
3. Results and Discussions
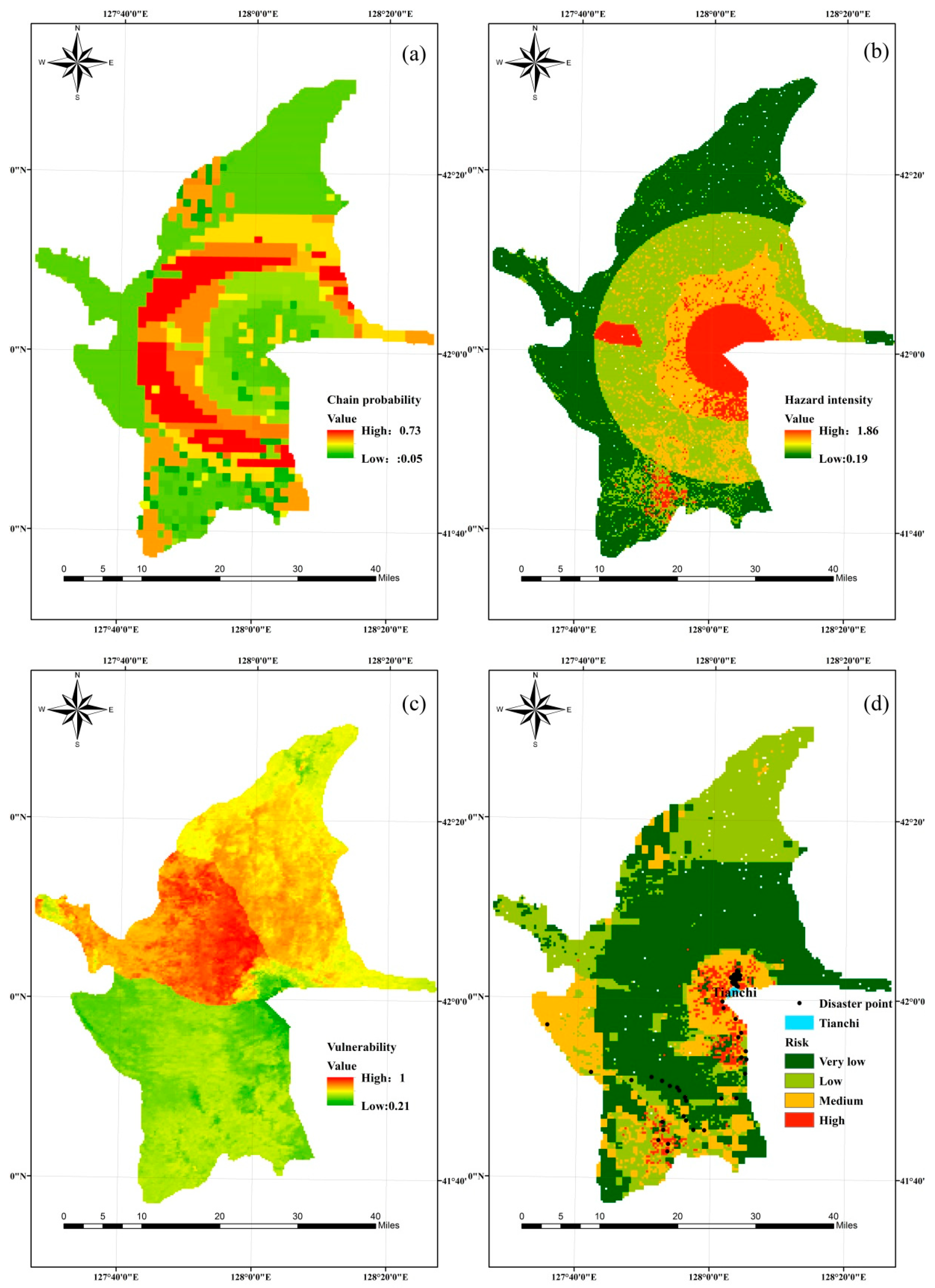
3.1. Earthquake Disaster Chain Hazard Analysis
3.1.1. Chain Probability Analysis
3.1.2. Hazard Intensity Analysis
3.2. Earthquake Disaster Chain Vulnerability Analysis
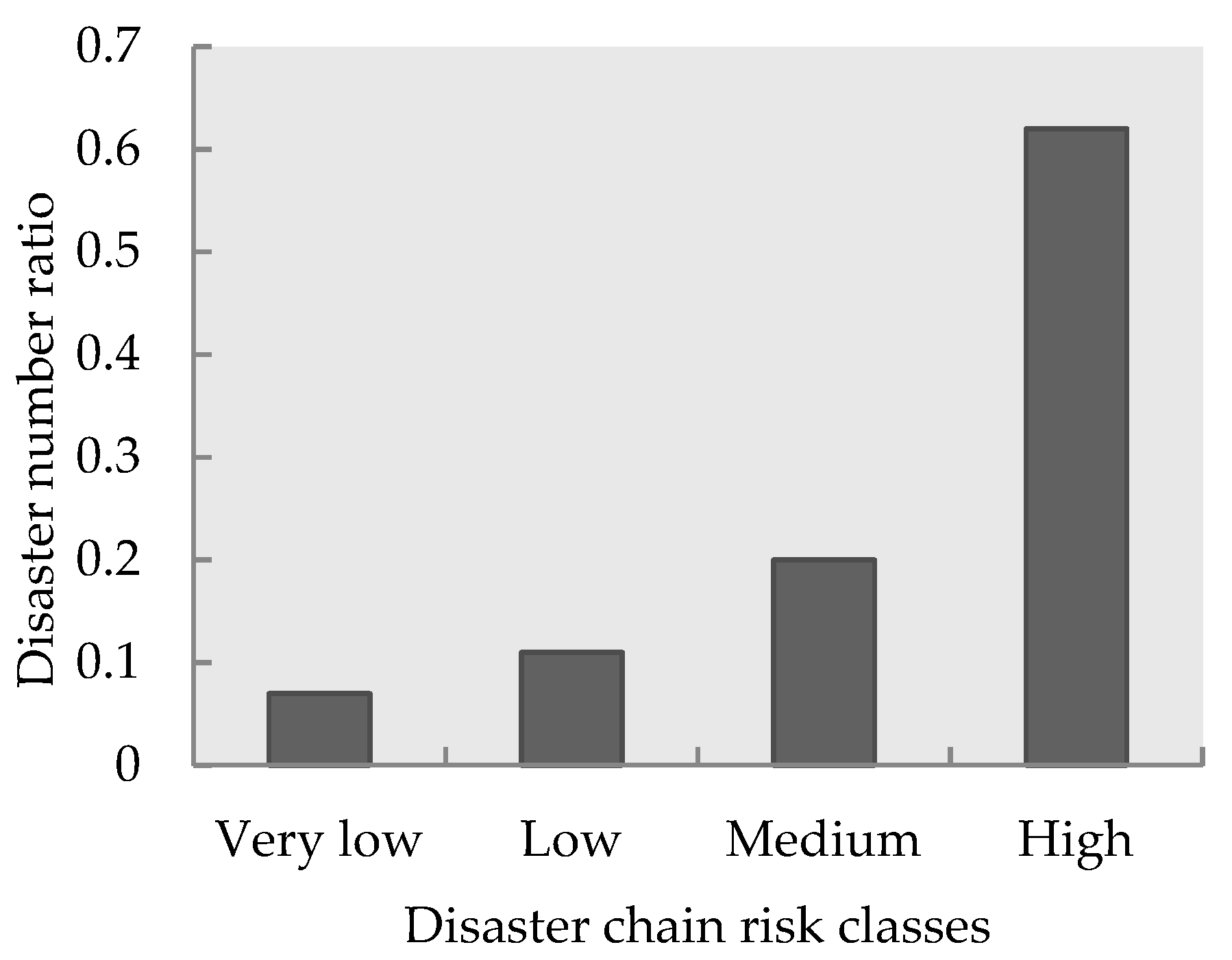
3.3. Earthquake Disaster Chain Risk Analysis
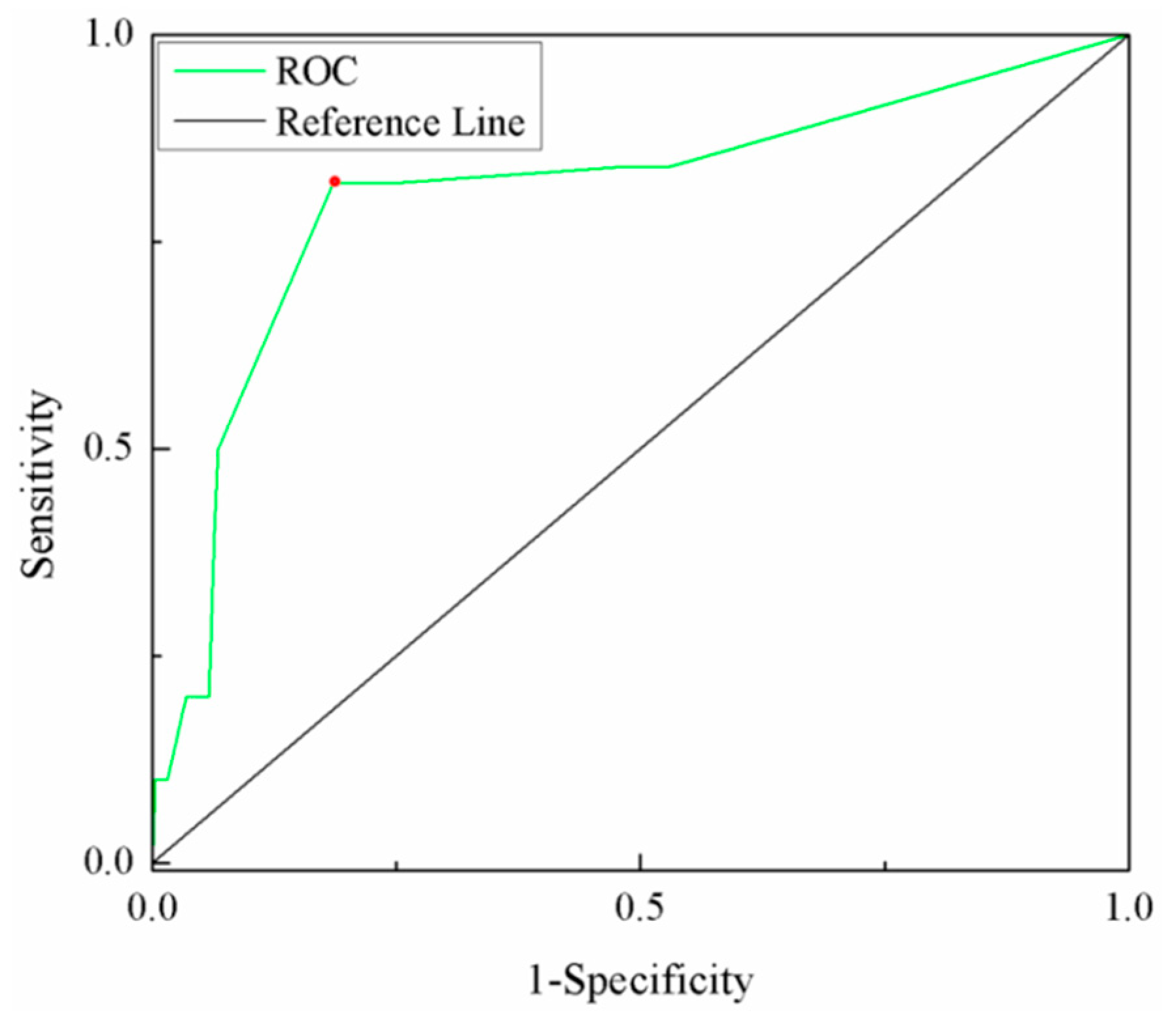
3.4. Validation of the Risk Assessment Model
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pei, R.R.; Ni, Z.Q.; Meng, Z.B.; Zhang, B.L.; Geng, Y.Y. Cause Analysis of the Secondary Mountain Disaster Chain in Wenchuan Earthquake. Am. J. Civ. Eng. 2017, 5, 414–417. [Google Scholar] [CrossRef]
- Lyu, H.-M.; Shen, J.S.; Arulrajah, A. Assessment of Geohazards and Preventative Countermeasures Using AHP Incorporated with GIS in Lanzhou, China. Sustainability 2018, 10, 304. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, S.; Huang, R. Multi-hazard scenarios and consequences in Beichuan, China: The first five years after the 2008 Wenchuan earthquake. Eng. Geol. 2014, 180, 4–20. [Google Scholar] [CrossRef]
- Yang, Z.H.; Lan, H.X.; Gao, X.; Li, L.P.; Meng, Y.S.; Wu, Y.M. Urgent landslide susceptibility assessment in the 2013 Lushan earthquake-impacted area, Sichuan Province, China. Nat. Hazards 2015, 75, 3467–3487. [Google Scholar] [CrossRef]
- Tian, Y.Y.; Xu, C.; Ma, S.Y.; Xu, X.W.; Wang, S.Y.; Zhang, H. Inventory and Spatial Distribution of Landslides Triggered by the 8th August 2017 M-W 6.5 Jiuzhaigou Earthquake, China. J. Earth Sci. 2019, 30, 206–217. [Google Scholar] [CrossRef]
- Hu, X.-D.; Hu, K.-H.; Zhang, X.-P.; Wei, L.; Tang, J.-B. Quantitative assessment of the impact of earthquake-induced geohazards on natural landscapes in Jiuzhaigou Valley. J. Mt. Sci. 2019, 16, 441–452. [Google Scholar] [CrossRef]
- Shi, P.J. Theory and practice of disaster study. J. Nat. Disasters 1996, 5, 8–19. (In Chinese) [Google Scholar]
- Cao, J.; Zhang, Z.; Wang, C.; Liu, J.; Zhang, L. Susceptibility assessment of landslides triggered by earthquakes in the Western Sichuan Plateau. Catena 2019, 175, 63–76. [Google Scholar] [CrossRef]
- Kwag, S.; Gupta, A. Probabilistic risk assessment framework for structural systems under multiple hazards using Bayesian statistics. Nucl. Eng. Des. 2017, 315, 20–34. [Google Scholar] [CrossRef]
- Korswagen, P.; Jonkman, S.; Terwel, K. Probabilistic assessment of structural damage from coupled multi-hazards. Struct. Saf. 2019, 76, 135–148. [Google Scholar] [CrossRef]
- Zheng, L.; Zheng, X.; Wang, F. Complex network construction method to extract the nature disaster chain based on data mining. In Proceedings of the 2017 7th IEEE International Conference on Electronics Information and Emergency Communication (ICEIEC), Macau, China, 21–23 July 2017; pp. 25–28. [Google Scholar]
- Liu, A.H.; Wu, C. Research on risk assessment method of disaster chain based on complex network. Syst. Eng. Theory Pract. 2015, 35, 466–472. [Google Scholar]
- Meena, S.R.; Ghorbanzadeh, O.; Blaschke, T. A Comparative Study of Statistics-Based Landslide Susceptibility Models: A Case Study of the Region Affected by the Gorkha Earthquake in Nepal. ISPRS Int. J. Geo-Inf. 2019, 8, 94. [Google Scholar] [CrossRef]
- Sharma, K.; Saraf, A.K.; Das, J.; Baral, S.S.; Borgohain, S.; Singh, G. Mapping and Change Detection Study of Nepal-2015 Earthquake Induced Landslides. J. Indian Soc. Remote Sens. 2018, 46, 605–615. [Google Scholar] [CrossRef]
- Tian, Y.Y.; Xu, C.; Hong, H.Y.; Zhou, Q.; Wang, D. Mapping earthquake-triggered landslide susceptibility by use of artificial neural network (ANN) models: An example of the 2013 Minxian (China) Mw 5.9 event. Geomat. Nat. Hazards Risk 2019, 10, 1–25. [Google Scholar] [CrossRef]
- Wang, Y.; Song, C.; Lin, Q.; Li, J. Occurrence probability assessment of earthquake-triggered landslides with Newmark displacement values and logistic regression: The Wenchuan earthquake, China. Geomorphology 2016, 258, 108–119. [Google Scholar] [CrossRef]
- Song, Y.; Gong, J.; Gao, S.; Wang, D.; Cui, T.; Li, Y.; Wei, B. Susceptibility assessment of earthquake-induced landslides using Bayesian network: A case study in Beichuan, China. Comput. Geosci. 2012, 42, 189–199. [Google Scholar] [CrossRef]
- Karray, M.; Hussien, M.N.; Souilem, M.; Locat, P.; Mompin, R. Adjustment of spectral pseudo-static approach to account for soil plasticity and zone seismicity. Can. Geotech. J. 2019, 56, 173–186. [Google Scholar] [CrossRef]
- Chang, K.-T.; Wan, S.; Lei, T.-C. Development of a spatial decision support system for monitoring earthquake-induced landslides based on aerial photographs and the finite element method. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, 448–456. [Google Scholar] [CrossRef]
- Cattoni, E.; Salciarini, D.; Tamagnini, C. A Generalized Newmark Method for the assessment of permanent displacements of flexible retaining structures under seismic loading conditions. Soil Dyn. Earthq. Eng. 2019, 117, 221–233. [Google Scholar] [CrossRef]
- Tang, Z.; Li, Y.; Hu, X.; Wu, H. Risk Analysis of Urban Dirty Bomb Attacking Based on Bayesian Network. Sustainability 2019, 11, 306. [Google Scholar] [CrossRef]
- Kabir, S.; Papadopoulos, Y. Applications of Bayesian networks and Petri nets in safety, reliability, and risk assessments: A review. Saf. Sci. 2019, 115, 154–175. [Google Scholar] [CrossRef]
- Wu, J.; Hu, Z.; Chen, J.; Li, Z. Risk Assessment of Underground Subway Stations to Fire Disasters Using Bayesian Network. Sustainability 2018, 10, 3810. [Google Scholar] [CrossRef]
- Vogel, K.; Riggelsen, C.; Korup, O.; Scherbaum, F. Bayesian network learning for natural hazard analyses. Nat. Hazards Earth Syst. Sci. 2014, 14, 2605–2626. [Google Scholar] [CrossRef] [Green Version]
- Ozdemir, A. Landslide susceptibility mapping using Bayesian approach in the Sultan Mountains (Akşehir, Turkey). Nat. Hazards 2011, 59, 1573–1607. [Google Scholar] [CrossRef]
- Macedo, J.; Bray, J.; Abrahamson, N.; Travasarou, T. Performance-Based Probabilistic Seismic Slope Displacement Procedure. Earthq. Spectra 2018, 34, 673–695. [Google Scholar] [CrossRef]
- Tsai, C.-C.; Lin, C.-H. Prediction of earthquake-induced slope displacements considering 2D topographic amplification and flexible sliding mass. Soil Dyn. Earthq. Eng. 2018, 113, 25–34. [Google Scholar] [CrossRef]
- Yue, X.L.; Wu, S.H.; Yin, Y.H.; Gao, J.B.; Zheng, J.Y. Risk Identification of Seismic Landslides by Joint Newmark and RockFall Analyst Models: A Case Study of Roads Affected by the Jiuzhaigou Earthquake. Int. J. Disaster Risk Sci. 2018, 9, 392–406. [Google Scholar] [CrossRef] [Green Version]
- Shinoda, M.; Miyata, Y. Regional landslide susceptibility following the Mid NIIGATA prefecture earthquake in 2004 with NEWMARK’S sliding block analysis. Landslides 2017, 14, 1887–1899. [Google Scholar] [CrossRef]
- Caccavale, M.; Matano, F.; Sacchi, M. An integrated approach to earthquake-induced landslide hazard zoning based on probabilistic seismic scenario for Phlegrean Islands (Ischia, Procida and Vivara), Italy. Geomorphology 2017, 295, 235–259. [Google Scholar] [CrossRef]
- Liu, J.M.; Shi, J.S.; Wang, T.; Wu, S.R. Seismic landslide hazard assessment in the Tianshui area, China, based on scenario earthquakes. Bull. Eng. Geol. Environ. 2018, 77, 1263–1272. [Google Scholar] [CrossRef]
- Chousianitis, K.; Del Gaudio, V.; Kalogeras, I.; Ganas, A. Predictive model of Arias intensity and Newmark displacement for regional scale evaluation of earthquake-induced landslide hazard in Greece. Soil Dyn. Earthq. Eng. 2014, 65, 11–29. [Google Scholar] [CrossRef]
- Del Gaudio, V.; Pierri, P.; Calcagnile, G. Analysis of seismic hazard in landslide-prone regions: Criteria and example for an area of Daunia (southern Italy). Nat. Hazards 2012, 61, 203–215. [Google Scholar] [CrossRef]
- Han, L.; Zhang, J.; Zhang, Y.; Ma, Q.; Alu, S.; Lang, Q. Hazard Assessment of Earthquake Disaster Chains Based on a Bayesian Network Model and ArcGIS. ISPRS Int. J. Geo-Inf. 2019, 8, 210. [Google Scholar] [CrossRef]
- Changbai Mountain Geological Disasters Investigation and Zoning Report (1:50000). Available online: http://gadri.net/pdf/Annual_Report_2017_GADRI_Final.pdf (accessed on 9 September 2019).
- Hua, Y.J.; Zhang, S.X.; Li, M.K.; Wu, T.F.; Zou, C.Y.; Liu, L. Magma system beneath Tengchong volcanic zone inferred from local earthquake seismic tomography. J. Volcanol. Geotherm. Res. 2017, 377, 1–16. [Google Scholar] [CrossRef]
- Oliva, S.J.; Ebinger, C.J.; Wauthier, C.; Muirhead, J.D.; Roecker, S.W.; Rivalta, E.; Heimann, S. Insights Into Fault-Magma Interactions in an Early-Stage Continental Rift From Source Mechanisms and Correlated Volcano-Tectonic Earthquakes. Geophys. Res. Lett. 2019, 46, 2065–2074. [Google Scholar] [CrossRef]
- Song, K.; Wang, F.W.; Dai, Z.L.; Iio, A.; Osaka, O.; Sakata, S. Geological characteristics of landslides triggered by the 2016 Kumamoto earthquake in Mt. Aso volcano, Japan. Bull. Eng. Geol. Environ. 2019, 78, 167–176. [Google Scholar] [CrossRef]
- Saito, H.; Uchiyama, S.; Hayakawa, Y.S.; Obanawa, H. Landslides triggered by an earthquake and heavy rainfalls at Aso volcano, Japan, detected by UAS and SfM-MVS photogrammetry. Prog. Earth Planet. Sci. 2018, 5, 15. [Google Scholar] [CrossRef]
- Uusitalo, L. Advantages and challenges of Bayesian networks in environmental modelling. Ecol. Model. 2007, 203, 312–318. [Google Scholar] [CrossRef]
- Sahin, O.; Stewart, R.A.; Faivre, G.; Ware, D.; Tomlinson, R.; Mackey, B. Spatial Bayesian Network for predicting sea level rise induced coastal erosion in a small Pacific Island. J. Environ. Manag. 2019, 238, 341–351. [Google Scholar] [CrossRef]
- Joseph, S.A.; Adams, B.J.; McCabe, B. Methodology for Bayesian Belief Network Development to Facilitate Compliance with Water Quality Regulations. J. Infrastruct. Syst. 2010, 16, 58–65. [Google Scholar] [CrossRef] [Green Version]
- De Beaufort, L.B.; Sedki, K.; Fontenelle, G. Inference reasoning on fishers’ knowledge using Bayesian causal maps. Ecol. Inform. 2015, 30, 345–355. [Google Scholar] [CrossRef]
- Kabir, G.; Tesfamariam, S.; Francisque, A.; Sadiq, R. Evaluating risk of water mains failure using a Bayesian belief network model. Eur. J. Oper. Res. 2015, 240, 220–234. [Google Scholar] [CrossRef]
- Tang, Z.; McCabe, B. Developing Complete Conditional Probability Tables from Fractional Data for Bayesian Belief Networks. J. Comput. Civ. Eng. 2007, 21, 265–276. [Google Scholar] [CrossRef]
- Geraldi, M.S.; Ghisi, E. Short-term instead of long-term rainfall time series in rainwater harvesting simulation in houses: An assessment using Bayesian Network. Resour. Conserv. Recycl. 2019, 144, 1–12. [Google Scholar] [CrossRef]
- Herskovits, E.H.; Cooper, G.F. Algorithms for Bayesian Belief-Network Precomputation. Methods Inf. Med. 1991, 30, 81–89. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jibson, R.W. Regression models for estimating coseismic landslide displacement. Eng. Geol. 2007, 91, 209–218. [Google Scholar] [CrossRef]
- Wilson, R.C.; Keefer, D. Predicting Areal Limits of Earthquake Induced Land sliding. Geol. Surv. Prof. Pap. 1985, 1360, 317–345. [Google Scholar]
- Shen, W.; Zhong, Q.; Shi, B. Synthetic seismic intensity for historic earthquakes in the North China Plain: Implications for the regional seismic hazard. Nat. Hazards 2014, 74, 305–323. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, G.; Shi, B.; Zhang, J.; Yang, Y. Development of seismic intensity attenuation model in North China and its application to quantitative estimation of earthquake location and magnitude. Acta Seismol. Sin. 2009, 3, 290–306. [Google Scholar]
- Ding, B.R.; Sun, J.J.; Li, X.D.; Liu, Z.W.; Du, J. Research progress and discussion of the correlation between seismic intensity and ground motion parameters. J. Earthq. Eng. Eng. Vib. 2014, 34, 7–20. [Google Scholar]
- Tiznado, J.; Opazo, C.; Silva, M.; Viejo, N. An Integrated Methodology for Displacement-Based Seismic Design of Homogeneous Slopes. Soil Mech. Found. Eng. 2018, 55, 16–24. [Google Scholar] [CrossRef]
- Jibson, R.W. Methods for assessing the stability of slopes during earthquakes—A retrospective. Eng. Geol. 2011, 122, 43–50. [Google Scholar] [CrossRef]
- Newmark, N.M. Effects of Earthquakes on Dams and Embankments. Géotechnique 1965, 15, 139–160. [Google Scholar] [CrossRef] [Green Version]
- Ingles, J.; Darrozes, J.; Soula, J.-C. Effects of the vertical component of ground shaking on earthquake-induced landslide displacements using generalized Newmark analysis. Eng. Geol. 2006, 86, 134–147. [Google Scholar] [CrossRef]
- Niño, M.; Jaimes, M.A.; Reinoso, E. Seismic-event-based methodology to obtain earthquake-induced translational landslide regional hazard maps. Nat. Hazards 2014, 73, 1697–1713. [Google Scholar] [CrossRef]
- Zhang, J.Q.; Okada, N.; Tatano, H. Integrated natural disaster risk management: Comprehensive and integrated model and Chinese strategy choice. J. Nat. Disasters 2006, 15, 29–37. [Google Scholar]
- Liu, Y.H.; Zhang, Z.X.; Su, Y.C. Case study of vulnerability evaluation for geo-hazards bearing capacity of a region. J. Eng. Geol. 2018, 26, 1121–1130. [Google Scholar]
- Rosanna, S.; Christopher, R.J.K. Forecasting eruptions after long repose intervals from accelerating rates of rock fracture: The June 1991 eruption of Mount Pinatubo, Philippines. J. Volcanol. Geotherm. Res. 2010, 191, 129–136. [Google Scholar]
- Huang, C.F.; Da, R.A. Fuzzy Risks and an Updating Algorithm with New Observations. Risk Anal. 2008, 28, 681–694. [Google Scholar] [CrossRef]
- Xue, Y.; Huang, C.; Huang, X.W. A new method and its application of handling fuzzy uncertainty of data in disaster risk assessment. In Proceedings of the 2009 WRI Global Congress on Intelligent Systems, Xiamen, China, 19–21 May 2009. [Google Scholar]
- Fotopoulou, S.D.; Pitilakis, K.D. Probabilistic assessment of the vulnerability of reinforced concrete buildings subjected to earthquake induced landslides. Bull. Earthq. Eng. 2017, 15, 5191–5215. [Google Scholar] [CrossRef]
- Fotopoulou, S.; Pitilakis, K. Vulnerability assessment of reinforced concrete buildings at precarious slopes subjected to combined ground shaking and earthquake induced landslide. Soil Dyn. Earthq. Eng. 2017, 93, 84–98. [Google Scholar] [CrossRef]
- Lei, T.-C.; Huang, Y.-M.; Lee, B.-J.; Hsieh, M.-H.; Lin, K.-T. Development of an empirical model for rainfall-induced hillside vulnerability assessment: A case study on Chen-Yu-Lan watershed, Nantou, Taiwan. Nat. Hazards 2014, 74, 341–373. [Google Scholar] [CrossRef]
- Pham, B.T.; Jaafari, A.; Prakash, I.; Bui, D.T. A novel hybrid intelligent model of support vector machines and the MultiBoost ensemble for landslide susceptibility modeling. Bull. Eng. Geol. Environ. 2019, 78, 2865–2886. [Google Scholar] [CrossRef]
- Harrell, F.E.; Lee, K.L.; Mark, D.B. Multivariable prognostic models: issues in developing models, evaluating assumptions and adequacy, and measuring and reducing errors. Stat. Med. 1996, 15, 361–387. [Google Scholar] [CrossRef]
| Engineering Geologic Types | |||
|---|---|---|---|
| Hard layer group: basalt | >0.22 | >37 | >26.5 |
| Secondary hard layer group: trachyte | 0.12~0.22 | 29~37 | >26.5 |
| Secondary soft layer group: tuff | 0.08~0.12 | 19~29 | 24.5~26.5 |
| Soft layer group: mudstone | <0.08 | <19 | <24.5 |
| Numbers | Risk | |||
|---|---|---|---|---|
| Actual | occurrence | non-occurrence | summation | |
| occurrence | TP:41 | FN:9 | TP+FN:50 | |
| non-occurrence | FP:1046 | TN:4826 | FP+TN:5872 | |
| summation | TP+FP:1087 | FN+TN:4835 | 5922 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, L.; Ma, Q.; Zhang, F.; Zhang, Y.; Zhang, J.; Bao, Y.; Zhao, J. Risk Assessment of An Earthquake-Collapse-Landslide Disaster Chain by Bayesian Network and Newmark Models. Int. J. Environ. Res. Public Health 2019, 16, 3330. https://0-doi-org.brum.beds.ac.uk/10.3390/ijerph16183330
Han L, Ma Q, Zhang F, Zhang Y, Zhang J, Bao Y, Zhao J. Risk Assessment of An Earthquake-Collapse-Landslide Disaster Chain by Bayesian Network and Newmark Models. International Journal of Environmental Research and Public Health. 2019; 16(18):3330. https://0-doi-org.brum.beds.ac.uk/10.3390/ijerph16183330
Chicago/Turabian StyleHan, Lina, Qing Ma, Feng Zhang, Yichen Zhang, Jiquan Zhang, Yongbin Bao, and Jing Zhao. 2019. "Risk Assessment of An Earthquake-Collapse-Landslide Disaster Chain by Bayesian Network and Newmark Models" International Journal of Environmental Research and Public Health 16, no. 18: 3330. https://0-doi-org.brum.beds.ac.uk/10.3390/ijerph16183330





