1. Introduction
Exposure to extreme temperature indoors or outdoors may have severe implications for human health. Gasparrini et al. [
1] estimated that 7.7% of the total mortality in 384 locations around the globe could be attributed to non-optimum ambient temperatures. In the forthcoming years, climate change will increase the intensity and frequency of extreme weather events, in particular, high temperatures [
2]. According to the European Environmental Agency, 80% of the European population is expected to live in urban areas by the year 2020, where health consequences of thermal exposures will be more severe [
3,
4,
5]. However, occupational risks related to thermal exposures of outdoor workers in rural areas may also increase.
The increasing risk of health impacts from future climate events requires the development of adaptation mechanisms that help people to withstand thermal stressful situations. Heat Shield [
6] and ClimApp [
7] are ongoing projects that will develop tools for better adaptation to suboptimal thermal environments. ClimApp is a smartphone application that combines climate forecasts, human thermal models, user characteristics and human physiology to improve decision making towards thermal adaptation strategies. Thermal exposure indoors is also considered within the scope of the ClimApp project since it affect the well-being, health and performance of building occupants in particularly fragile populations such as the elderly or young children [
8,
9]. The estimation of indoor air temperature is essential for the evaluation of thermal comfort and energy consumption in built environments [
10,
11]. In ClimApp, the estimated temperature will be used as input to the calculation of the Predicted Mean Vote index (PMV). On a seven-point scale ranging from cold to hot, the PMV predicts the average thermal sensation of a group of people exposed to the same thermal conditions [
11]. Other input parameters required to calculate PMV are the mean radiant temperature, air humidity, mean air velocity, clothing insulation and metabolic rate. These five parameters will be estimated based on season, geographical location and simple user input. In the future, smartphones with built-in or auxiliary thermal environment sensors may be a useful tool to assess people’s local thermal environment. However, even though most phones are equipped with temperature sensors, they only measure the internal temperature in the phone, which may be heated, e.g., by the phone’s electronics or from lying in a pocket. Technology to measure the thermal environment that occupants are exposed to is not yet fully developed or commonly available [
12].
The indoor air temperature depends on multiple factors related with building characteristics, occupants and outdoor climate. Nguyen et al. [
13,
14] observed that the degree to which indoor and outdoor temperatures are associated depends on the climatic region and that the association is particularly strong during warm seasons. Oreszcyn et al. [
15] analysed different factors that influenced indoor temperatures in 1600 low-income English dwellings during the heating season. Their findings indicated that indoor temperatures depended mostly on building characteristics (e.g., construction year and thermal efficiency-related factors, such as insulation level, air tightness of the building envelope) and occupant-related factors (e.g., age and number of occupants). Hamilton et al. [
16] found that indoor temperatures in English houses increased with increasing household income and that old houses had significantly lower indoor temperatures than new houses. French et al. [
17] analysed temperature data from 400 houses in New Zealand. Their results showed that heating type, climate and house age had the largest influence on winter indoor temperatures, whereas the availability of air conditioning, house age and outdoor climate influenced temperature levels more during summer. Magalhães et al. [
18] also analysed the factors that influence indoor temperatures using enhanced linear regression models with measurements from field studies in 141 dwellings. Their findings showed that the variability of daily mean indoor air temperatures was influenced by building characteristics (73% to 85% of the surveyed households), socio-economic factors (4% to 14% of the surveyed households) and outdoor air temperatures (1% to 3% of the surveyed households). Building characteristics included parameters such as age of construction, wall insulation, window characteristics and type of space heating equipment. Moreover, their method to estimate indoor temperature showed a high predictive performance (R
2 from 0.89 to 0.91) when comparing predicted and measured temperature values. White-Newsome et al. [
19] applied mixed linear regression models to predict hourly indoor temperature measurements during summer in 30 residences. The combination of outdoor temperature, solar radiation and dew-point temperature explained 38% of the variability in the indoor temperature values in their study. Several studies developed more advanced techniques for indoor temperature prediction than merely linear regression models. Some of them used Time-Series analysis [
20] and others used a combination between Time-Series and Artificial Neural Networks (ANN) [
21,
22,
23,
24]. Time-Series is an approach used for data forecasting based on statistical analysis of measured values over a defined period. Such a method is normally used for Model Predictive Control (MPC), applied in modern Heating, Ventilation and Air-Conditioning (HVAC) operation strategies. Mateo et al. [
25] applied different machine learning techniques to forecast indoor air temperatures based on outdoor climate parameters (air temperature and relative humidity) and variables related to space heating use (temperature set point and heating power). Their approach focused on short-term temperature forecasting (24 h), reaching an average error of approximately 0.1 °C. The framework proposed by Kelly et al. [
26] was able to predict indoor air temperatures with an error of 0.71 °C at 95% confidence. Their method used behavioural, environmental and building efficiency variables as inputs, which were processed through panel Time-Series methods. In general terms, the outcome of Time-Series forecasting is restricted to the specific design and operation conditions of a building. Its complexity prevents its implementation in smartphone applications.
The framework suggested in this study uses occupants’ observations and weather data as input to estimate indoor air temperatures. It is expected that the indoor module of the App will be particularly useful in environments hosting fragile individuals, such as young children and the elderly, and where heat or cold spells may result in unusual thermal exposures. Under these conditions, the App’s output may assist in an evaluation of coping actions. All input parameters were combined through a decision tree algorithm which was constructed based on measured data and building characteristics obtained from field studies. The framework was developed to be integrated into ClimApp to enable the assessment of thermal exposures indoors by calculating the Predicted Mean Vote based on weather data and simple building descriptors. The scope of this paper is limited to the development of a prediction framework for indoor air temperature.
4. Discussion
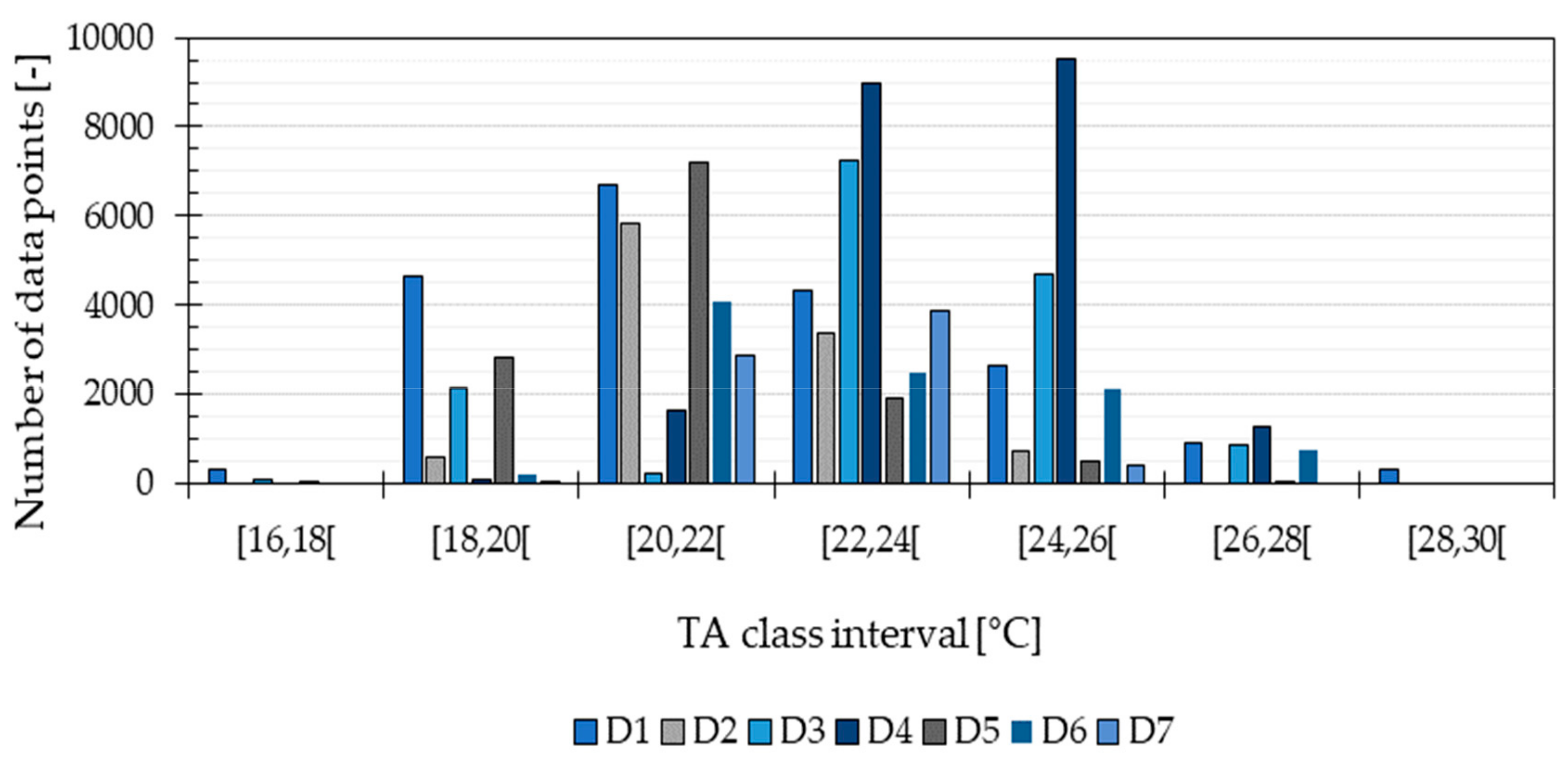
As expected, the measured TA values were not evenly distributed among the different temperature classes. In particular, none of the dwellings except D3 provided TA values inside all classes. As described by Liu et al. [
32], when a binning discretization method is used (division of a continuous attribute into a specified number of bins), there is a trade-off between creating classes with equal frequency and creating classes with equal width. In this study, discretizing the TA values comprised the creation of temperature ranges with equal width to define beforehand an estimation of the uncertainty of every TA value predicted, corresponding to ±1 °C. This definition caused an uneven distribution of the data records used to develop the classification algorithm, but it may have allowed predicting the PMV with reasonable accuracy.
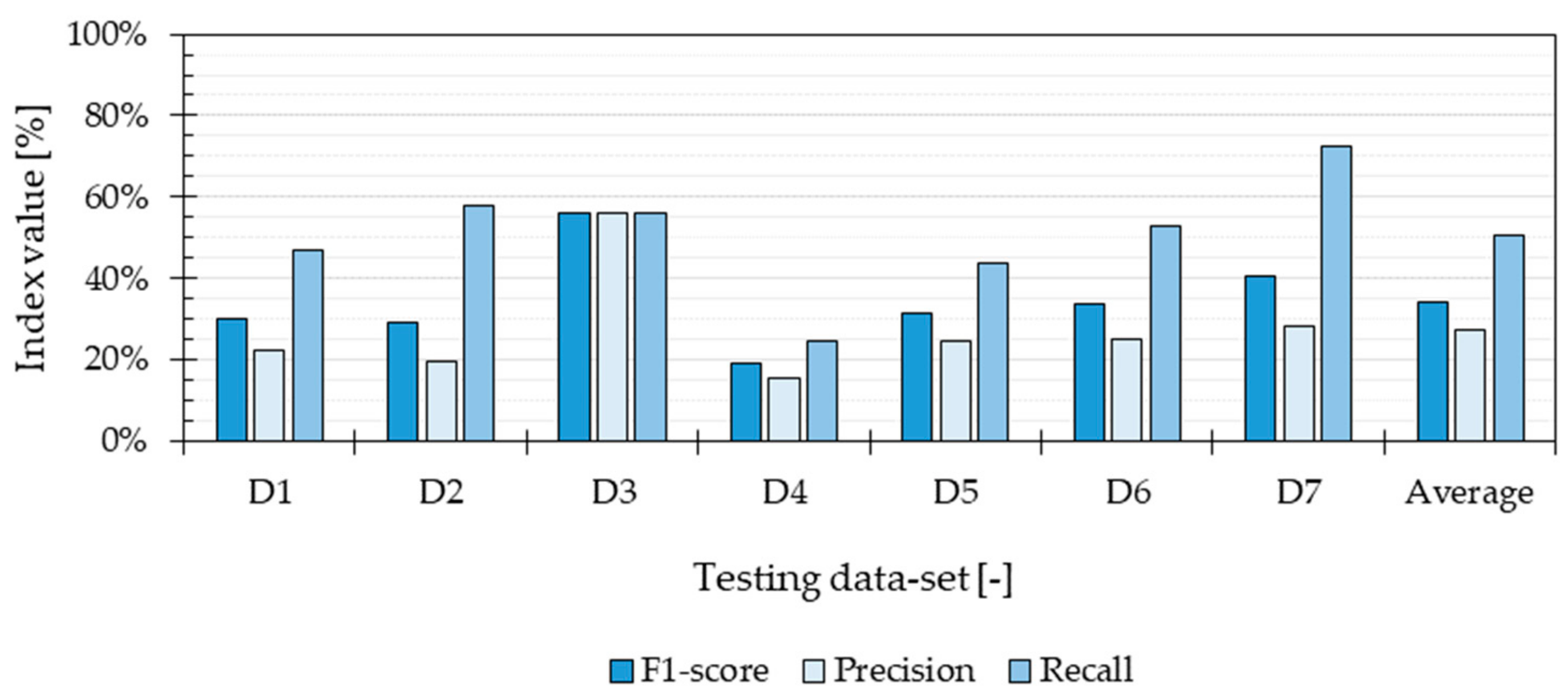
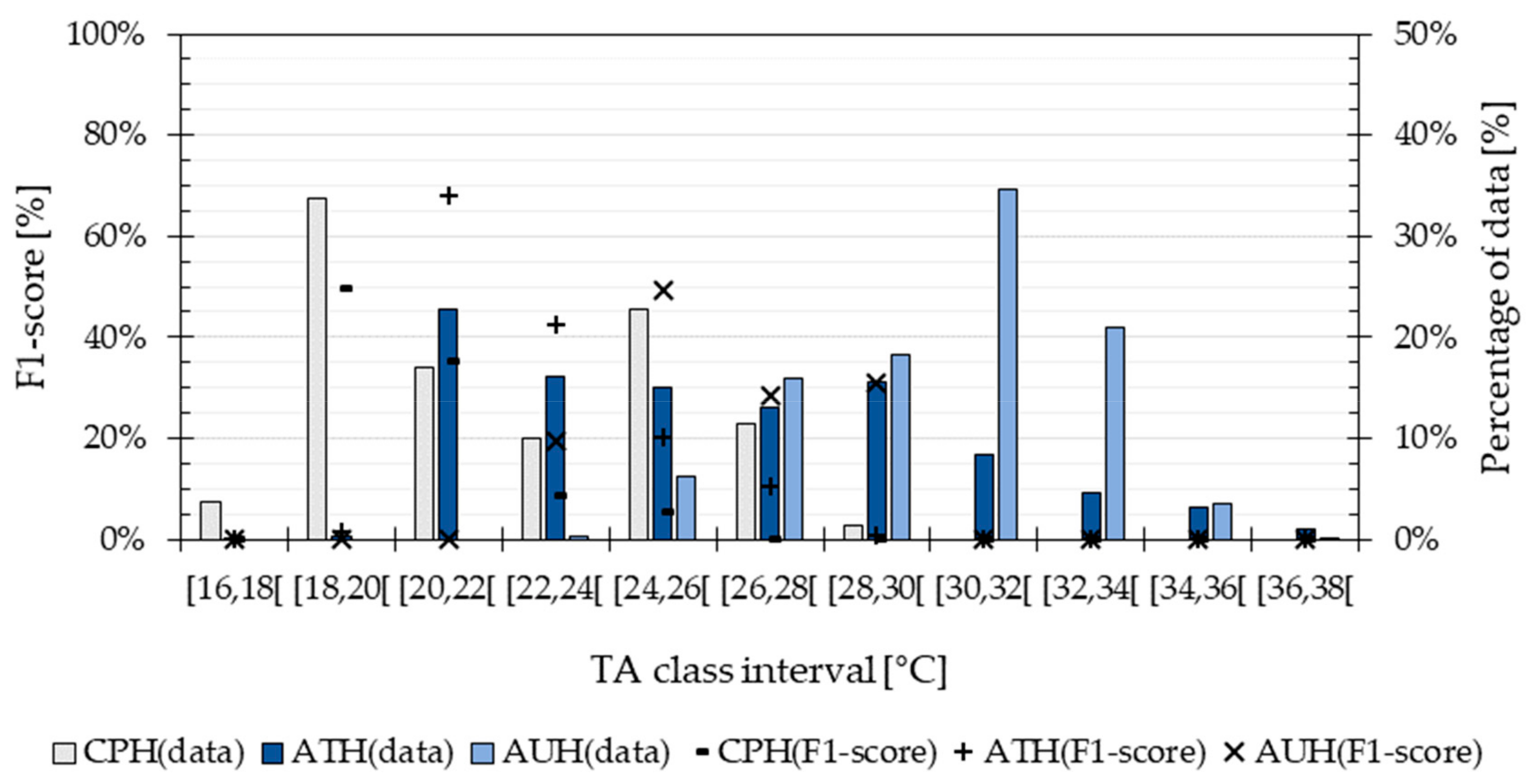
The outcome of the Validation evaluation shows that the algorithm had a performance of 92%, estimated based on its precision, recall and F1-score. However, the training data and validation data were separate data sets extracted from the same group of measured values. Therefore, the distribution of the training data and the data used for validation was similar, which explains the similarity between recall and precision. The Validation evaluation showed that the algorithm’s performance is probably high when the testing conditions are taken into consideration during the training phase. This means that the magnitude of variables, such as type of building, outdoor climate, heating system and occupant behaviour were similar during the training and testing phases. However, such type of evaluation did not estimate how generalizable the TA-prediction method may be. The Application evaluation showed that the performance of the algorithm decreased significantly when tested in a completely different dwelling (
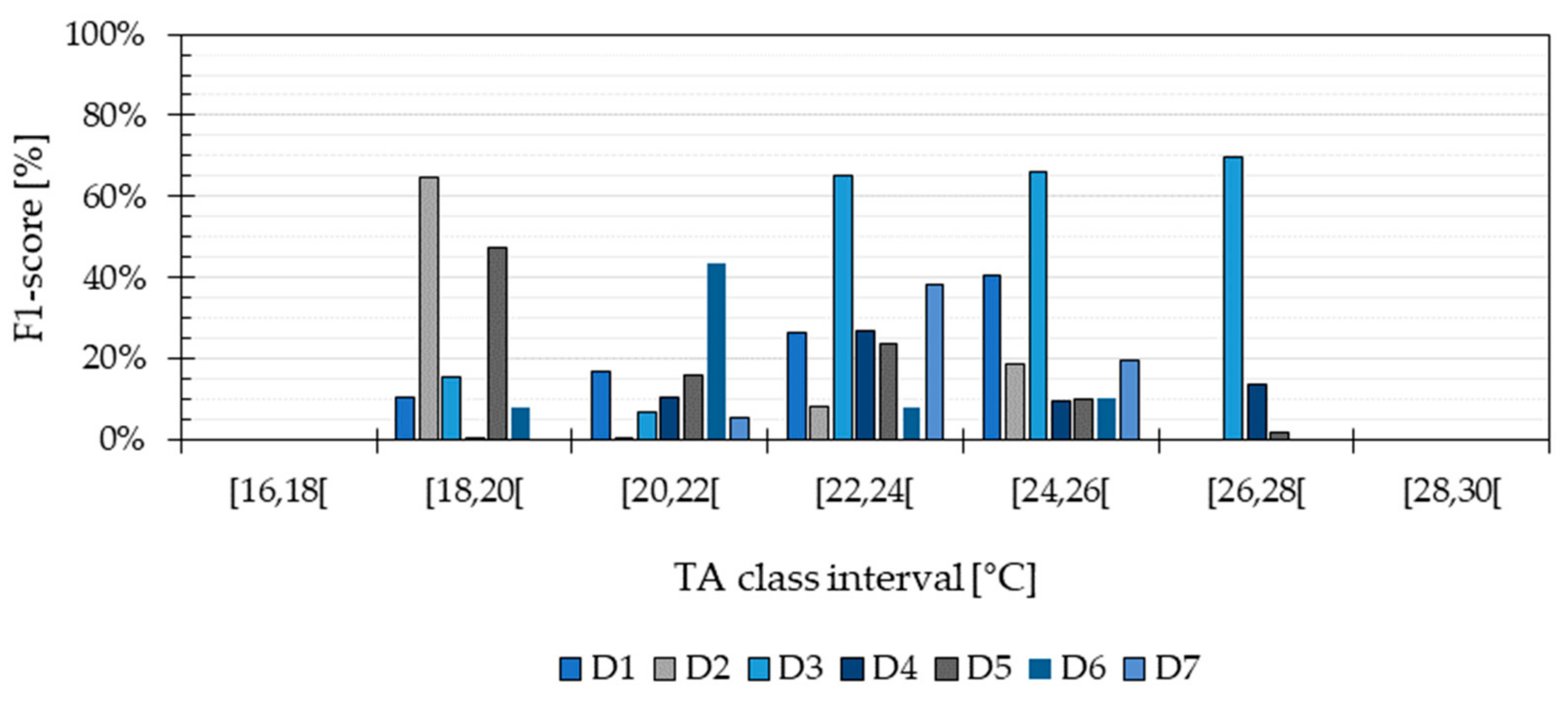
Figure 4). The prediction performance was affected by an uneven distribution of TA values across the predicted classes, producing differences between the obtained recall and precision. The results show that the method presented in this study had a higher probability of predicting correctly the most prevalent temperatures in the different dwellings. The discretization of the TA measurements prevented the method from correct estimations in temperature categories lacking data points. This class imbalance is unavoidable, given that in reality, it is not possible to have equal number of measured TA values during equal periods. Predicting incorrectly the most extreme temperature values implies that the method will not be able to assess the most critical situations when occupants are under unacceptable thermal environments (e.g., inactive heating system during winter, windows opened during cold outdoor temperatures). However, one evident solution to increase the prediction performance of the excessively high or low indoor temperatures is to use training data from a longer period. As suggested by Japkowicz and Stephen [
44], increasing the size of the training set decreases the effect of the class imbalance, improving the performance of the method. For that, the training set should account for variations of TA values during different seasons, where the heating and cooling needs change.
The initial criteria to select the input parameters was to include variables that can be obtained from weather services online and from relatively simple user-provided feedback. The literature review presented in the introduction showed that building-related parameters, outdoor climate and occupant behaviour had an effect on indoor temperature values in several studies [
13,
14,
15,
16,
17,
18,
19,
20,
21,
22,
23,
24,
25,
26]. A comprehensive database extracted from field studies [
27,
28] was used to train and test the method. This database contained building descriptors (floor area and construction year) and occupant behaviour (heating set point, window opening and nominal occupancy level). However, since the database was obtained only from one climatic zone (Copenhagen, Denmark), the method was tested under different climate conditions using dynamic simulations. Even though eight parameters were used as inputs, the results from
Table 7 show that not all of them had the same impact on the performance of the method. Depending on the parameters considered, using more descriptors has the potential to improve the prediction performance. Nonetheless, this will probably make the task of getting input from occupants more difficult and may induce over-fitting (a predictive model that is highly specific to only one set of data [
45]).
Based on the building simulation analysis, it was found that the outdoor climate affected the performance of the TA-prediction method, which also had an impact on building-related attributes used as input parameters. The method had its highest performance (68%) when predicting the most frequent TA values. Hence, the training data should account for a wide range of temperatures evenly distributed among the TA prediction classes. When the method was applied to the data from Copenhagen and Athens, three attributes were relevant as input to predict TA (solar radiation, hourly running mean temperature, and number of occupants), whereas only two variables (relative humidity outdoors and solar radiation) were important when using the data from Abu Dhabi. The simulations considered the same building type for Copenhagen, Abu Dhabi and Athens using Danish construction regulations. According to the studies from Böhnke [
46] and Giusti and Almoosawi [
47], a representative dwelling for Athens and for Abu Dhabi is less tight with significantly higher heat losses than a Danish household. Nevertheless, the building type was not changed in the simulations performed in this study to better analyse the influence of climate-related parameters on the performance of the method.
The hourly running mean outdoor temperature was calculated based on past hourly values of outdoor temperature. Due to the thermal mass of a building, the outdoor air temperature does not have an instant effect on the air temperature indoors, which explains the importance of TRM as an input parameter to estimate TA. Vant-Hull et al. [
48] observed that hourly averages of indoor and outdoor temperatures were correlated with a time lag of 2 h, based on a study performed in 30 residences located in New York City, USA. Their results differed with the period of 3 h considered to calculate the TRM in this study, probably due to discrepancies between the thermal mass of the buildings analysed in both studies. The results were in agreement with the findings from Nguyen et al. [
14] and French et al. [
17], since the TA predictions depended on outdoor climate variables (TRM and RHO) during the warm season. Building-related parameters, such as CY and FA, only had a modest influence on the prediction performance, regardless of how well they correlated with the TA values and their Information Gain measure. The results were not entirely in accordance with the studies by Oreszyn et al. [
15], which observed that TA values in households were influenced by building age. Their study was carried out during wintertime, when the building envelope characteristics have a more noticeable effect on the temperature indoors. The field study presented in this paper was not restricted to a single season as it was performed during winter, spring and summer. Therefore, the TA values were probably less dependent on the envelope of the buildings analysed. Moreover, the study by Kragh and Wittchen [
38] showed that the overall heat transfer coefficient of Danish dwellings did not change significantly during the years that the households analysed in this study were originally constructed (between 1928 and 1981). However, Oreszyn et al. [
15] found that the number of occupants was a factor that significantly affected the TA values, which is in accordance with the results from this study. The presence of humans in indoor environments increases the heat load and therefore, TA, which varies depending on the number of occupants and most likely, their metabolic activity rate. The parametric analysis in the current study only analysed the absence of one attribute at a time, evaluating its influence on the overall performance of the method. In practice, more than one parameter can be missing or some of them can be incorrectly provided by the App user. This type of issue will probably have a greater effect when predicting TA values, which were not possible to estimate in this study.
The results suggest that the relationships between the different parameters used in the model and TA are context-dependent. Diverse heating/cooling systems may have a larger or smaller influence on TA (i.e., higher or lower influence of TRV), which could be caused by technologies using different heat transfer principles or because of different climates. Furthermore, occupants’ control possibilities over their thermal environment could be reduced or even non-existent in some cases, whereas in other buildings with personal control systems, individuals are able to control their immediate surroundings. Even though the value of TA relies on the context, it is evident that the outdoor climate parameters have multiple direct or indirect possibilities to influence the TA values. Namely, they have an effect over human behaviour, over the performance of heating/cooling systems and a direct influence over TA. A TA-prediction model is not capable of generalizing such relationships for all different circumstances (e.g., different building types, climates, human behaviour). Nevertheless, the framework presented in this study is able to learn from those circumstances, making meaningful predictions of TA.
The main outcome of this study was a method to predict indoor air temperature to estimate PMV and assess indoor thermal comfort with incomplete knowledge of the real thermal conditions. When the method has been implemented in the app, the user may enter specific information on the building and behaviour related parameters, such as the state of thermostats or window opening, which will increase the accuracy of the predicted exposure. The user may also be unaware of these building descriptors, in which case default values will be used as input to the PMV prediction. Thus, in addition to the uncertainty of the predicted indoor air temperature, several other factors will affect the accuracy of the estimated PMV. Therefore, a conservative approach should be used when users apply the app to assess thermal strain indoors. This can be done by introduction of a safety margin, e.g., corresponding to the uncertainty shown in
Table 8. Under non-comfort conditions, the predicted air temperature may also be used to calculate other indices, typically with more extreme thermal exposures that are more common outdoors, such as the wet-bulb globe temperature (WBGT), predicted heat strain (PHS), or required clothing insulation (IREQ) [
49,
50,
51].These other indices are already used in the app to assess outdoor thermal exposure. After implementation of the suggested method in the app, its functionality will be tested in a range of field studies as part of the ClimApp project.
The framework presented in this study neglects the time-dependent nature of the parameters used to develop the model using a classification approach rather than a time-series regression model to predict indoor air temperatures. Moreover, it applies univariate discretization only based on temperatures, which inevitably also divides the input parameters into categories, affecting its prediction performance. However, the application of a more complex discretization approach or a regression model that accounts for time-dependent variations will increase the need for more computing power. The simplicity of the method proposed in this paper is grounded in the possibility of its application into mobile devices, giving a meaningful thermal evaluation of users’ indoor environments. Additionally, this method could be used in future research studies to develop techniques to monitor indoor environments with fewer or no sensors. Tronchin et al. [
52] highlighted the importance of limiting the number of sensors in buildings to increase the possibility of monitoring at multiple scales.
The generalization of the TA-prediction model depends on its ability to produce correct predictions under different conditions (e.g., building type, climate, occupants). The measured data considered in this study accounted for only one climate and one building code. The simulated data had a wider geographical scope to include different climates and improve the generalizability of the prediction. However, more research efforts should be made to develop a comprehensive database that allows the analysis of building performance, indoor environment and occupant behavior under an even wider range of conditions and improves the prediction power of data-driven models.