Risk Assessment of High-Speed Rail Projects: A Risk Coupling Model Based on System Dynamics
Abstract
:1. Introduction
2. Literature Review
2.1. The Risks for the High-Speed Rail Project
2.1.1. Vulnerability Risk
2.1.2. Threatening Risk
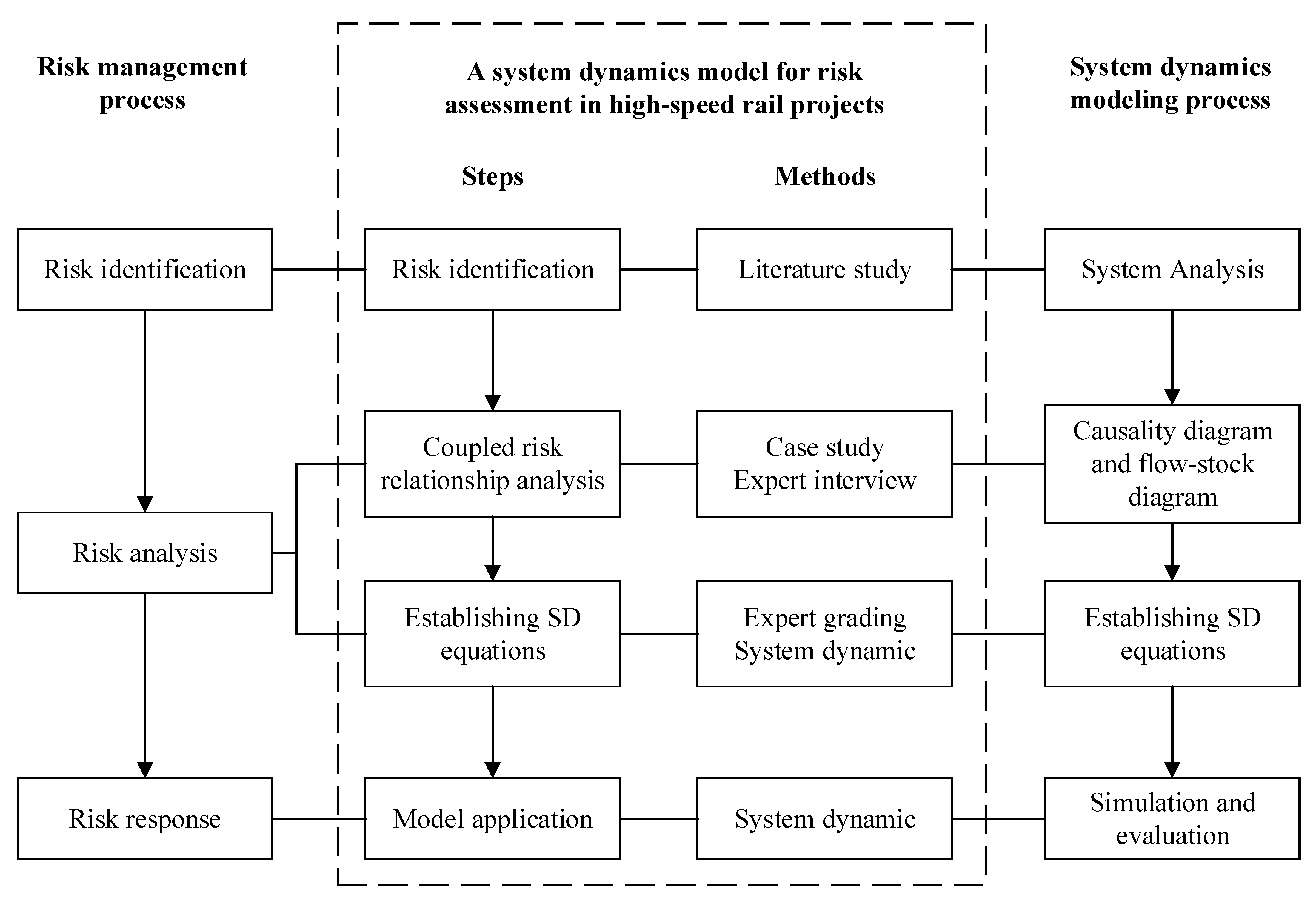
2.2. Risk Assessment Methods and System Dynamics
- System Analysis. To articulate the problem and determine the boundary of the system and subsystem; that is, to determine the scope of the study.
- Causality diagram and flow-stock diagram. To analyze the relationships between the system components and qualitatively describe these in a causality diagram. On this basis, the components are defined as different variable types, which are displayed in the flow-stock diagram.
- Establishing SD equations. This step designs functions to clarify the quantitative relationships among variables in the system and estimate parameter values for use in the equations.
- Simulation and evaluation. After setting the simulation time and step size in the SD software, the status of each variable and the whole system can be simulated within a period of time or at a certain time node. Further, the simulation results can be compared by varying the values of the variables in the SD equations.
3. Methodology
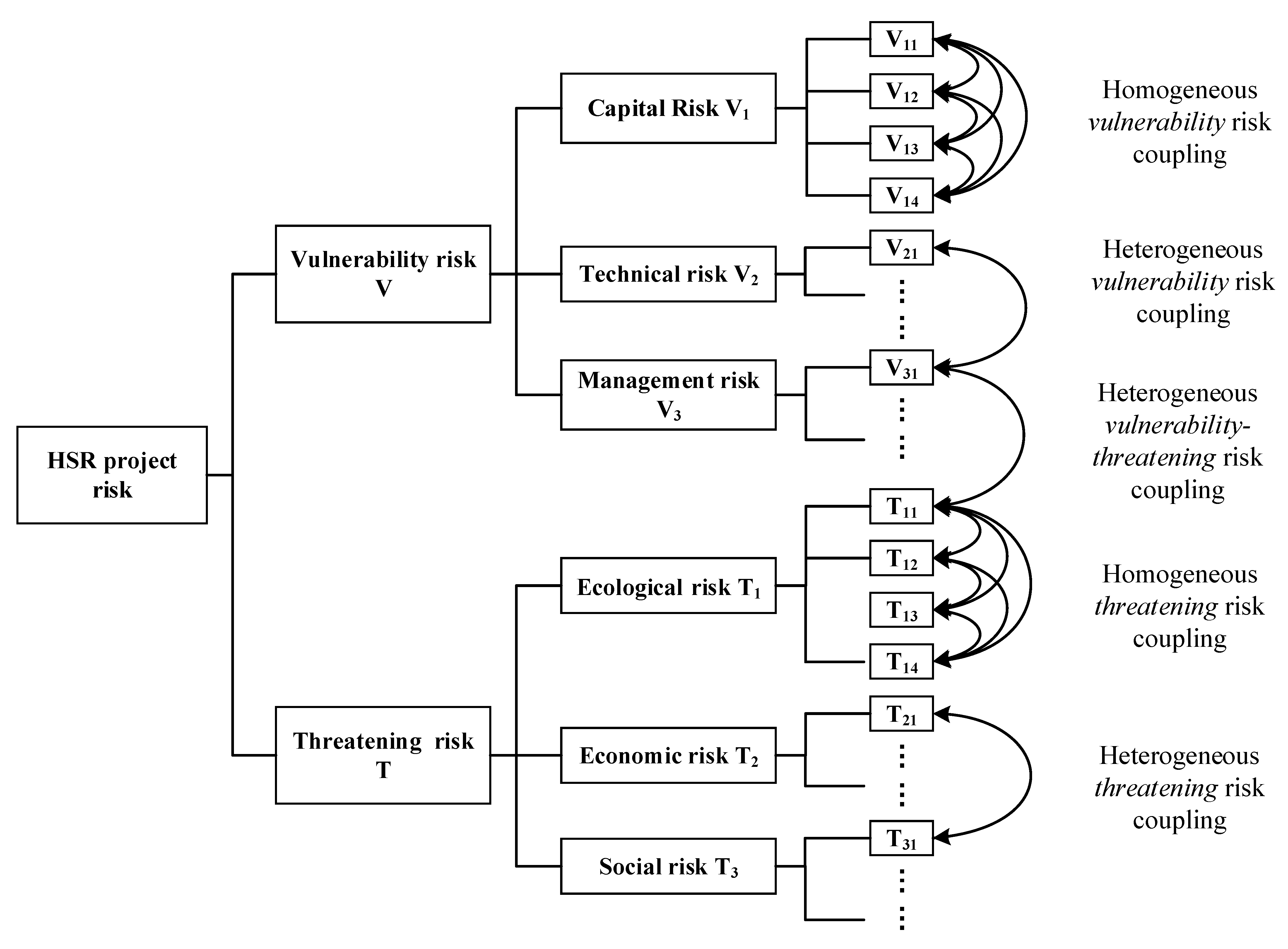
4. Coupled Risk Relationship Analysis
4.1. Risk Coupling in the Vulnerability Risk Subsystem
4.1.1. Homogeneous Coupling of Vulnerability Risks
4.1.2. Heterogeneous Coupling of Vulnerability Risks
4.2. Risk Coupling in the Threatening Risk Subsystem
4.2.1. Homogeneous Coupling of Threatening Risks
4.2.2. Heterogeneous Coupling of Threatening Risks
4.3. Risk Coupling Between the Vulnerability and Threatening Risk Subsystems
5. Establishing System Dynamics Equations
5.1. Risk Assessment System and Weights of Indicators
5.2. Valuation of Risk Factors
5.3. Calculation of Coupling Coefficient
5.4. Completing System Dynamics Equations
6. Model Application to the Zhengzhou-Wanzhou High-Speed Rail Project
6.1. Project Overview
6.2. Data Collection and Processing
6.3. Simulation and Results Analysis
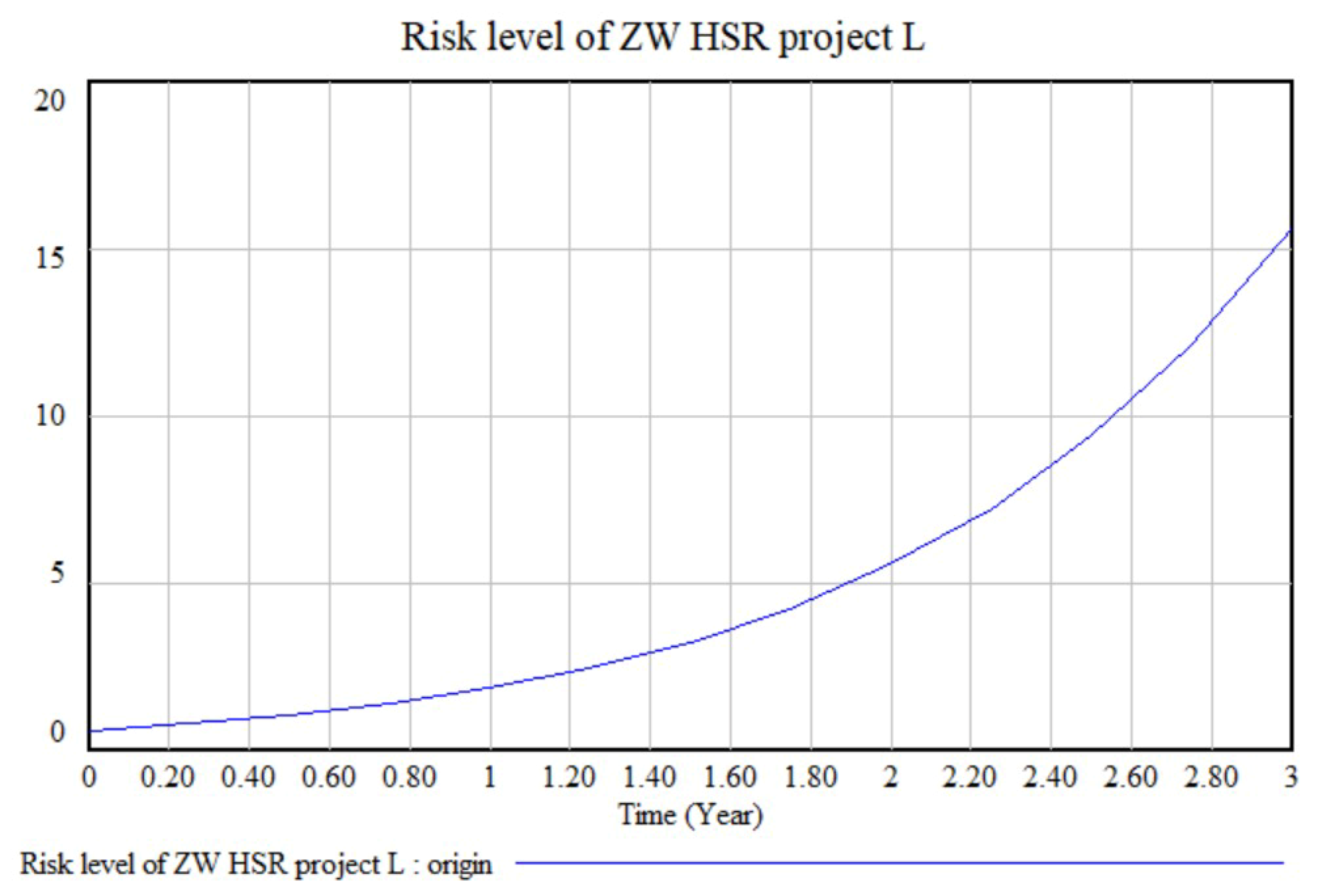
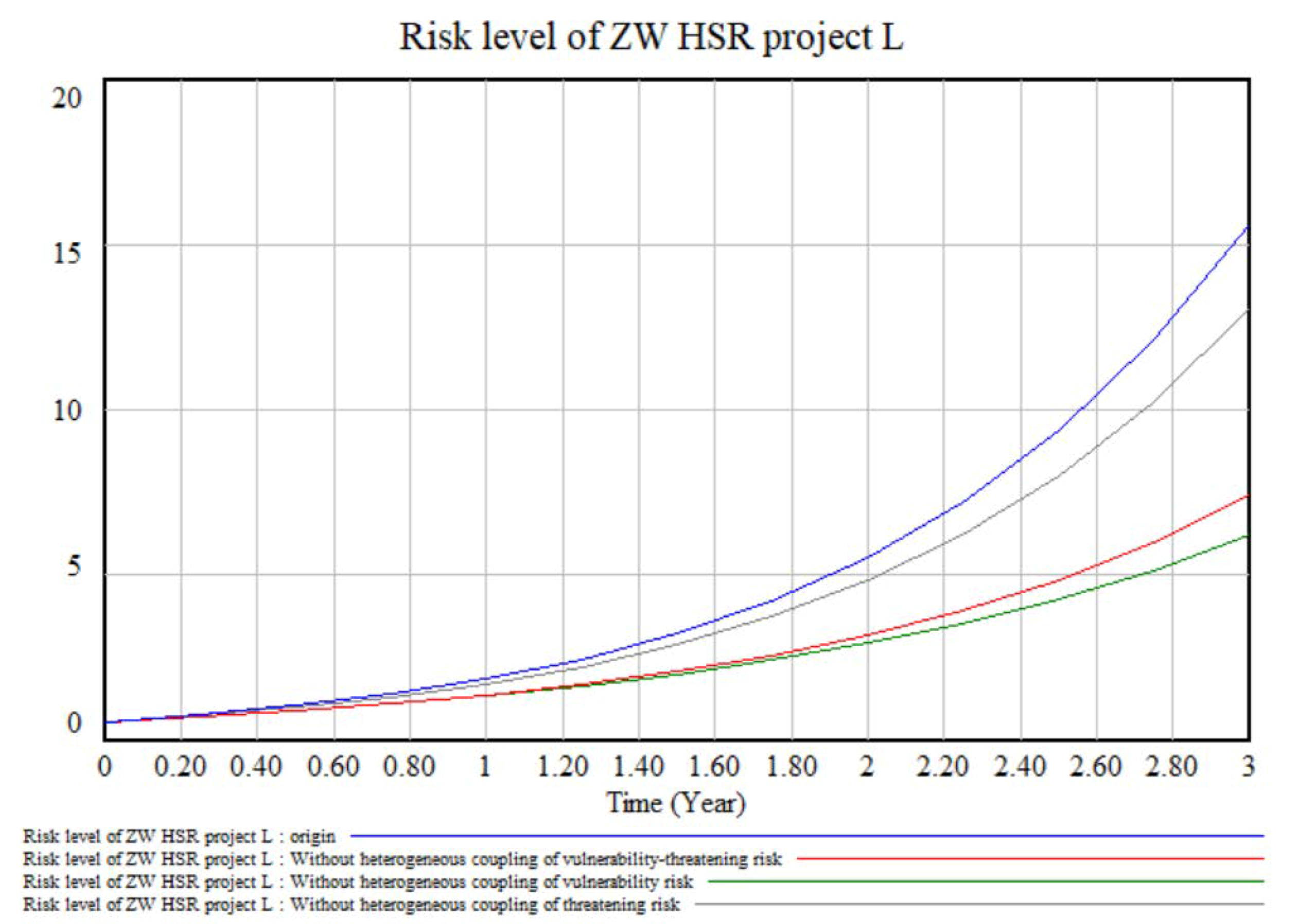
6.3.1. Analysis of Risk Level Results
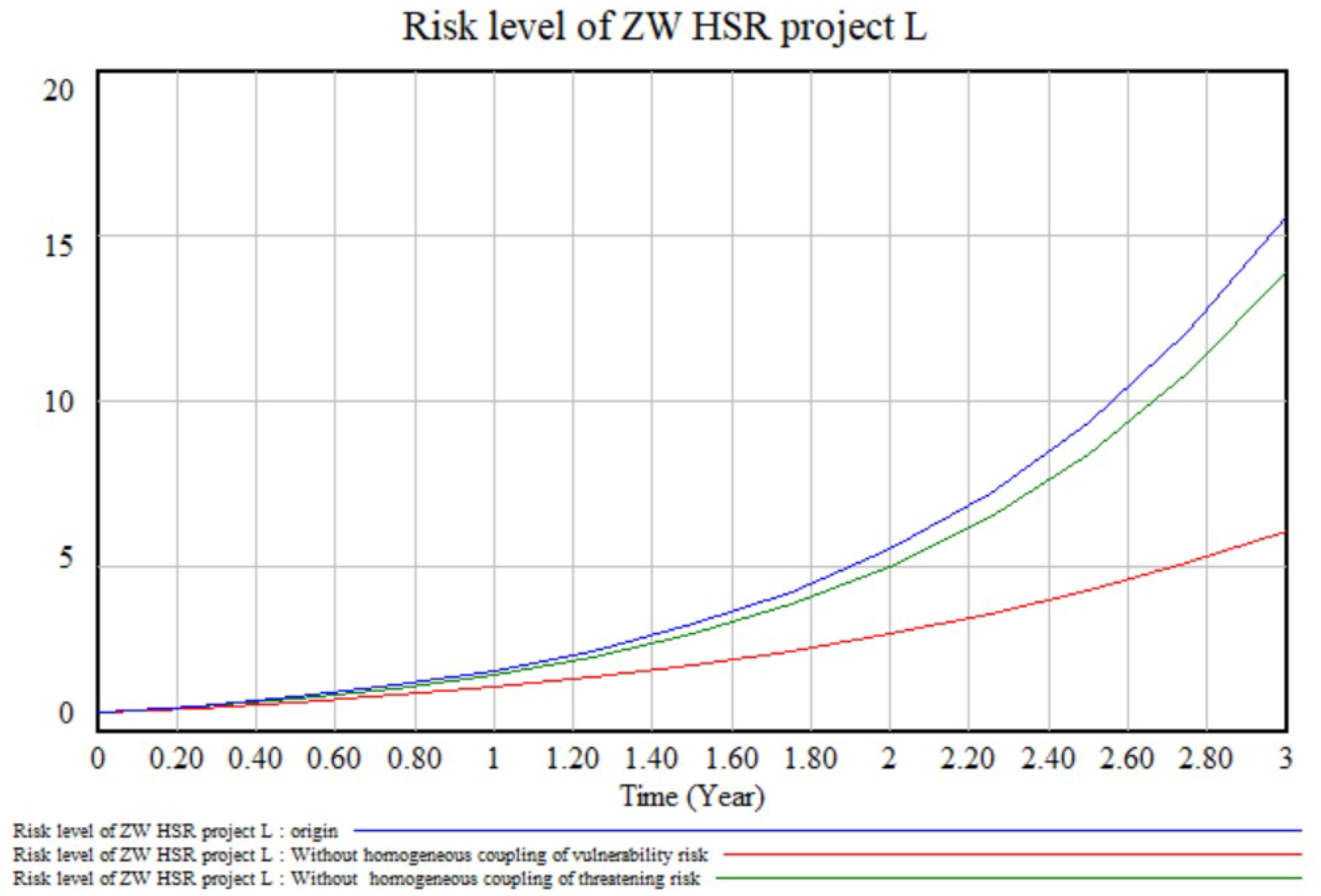
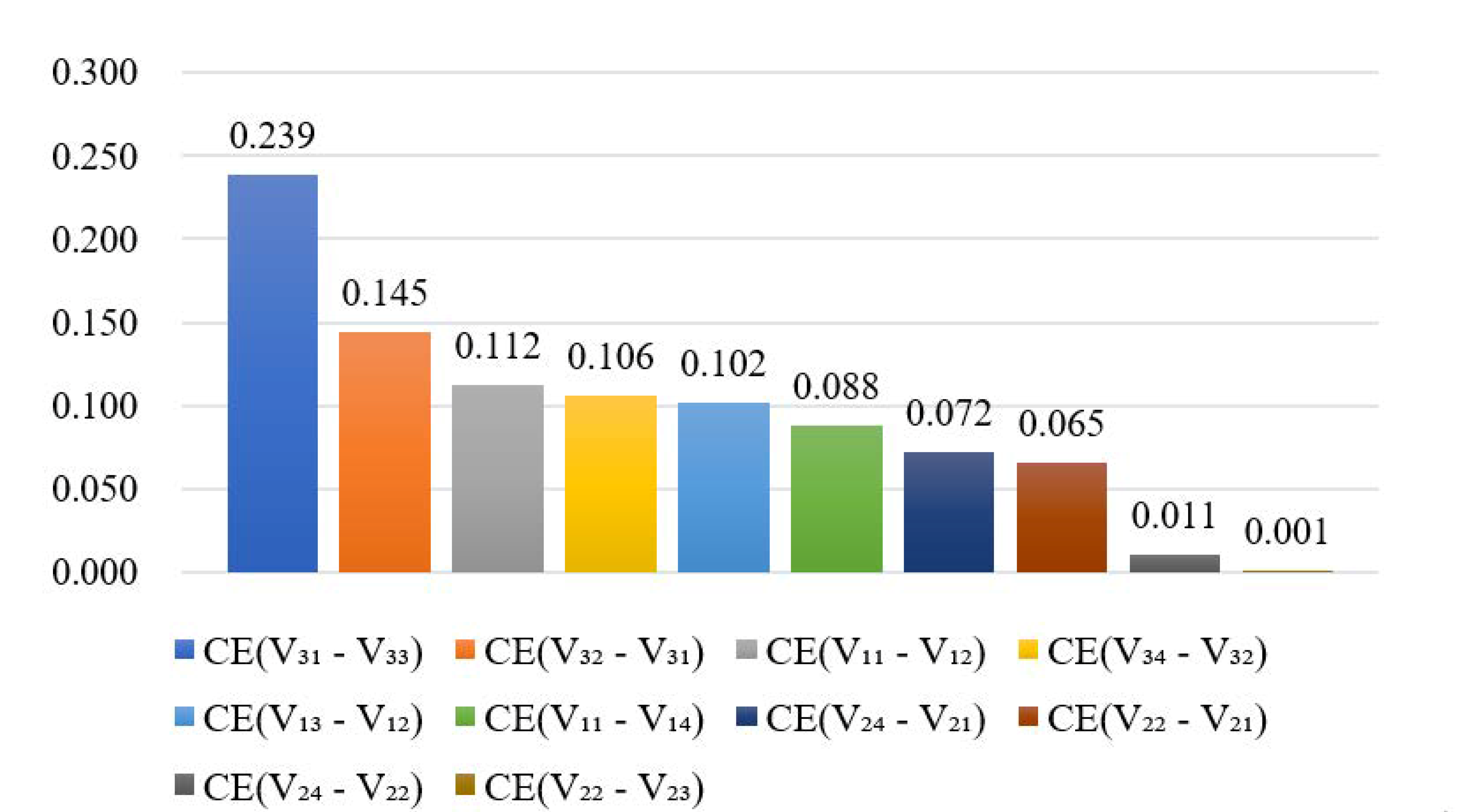
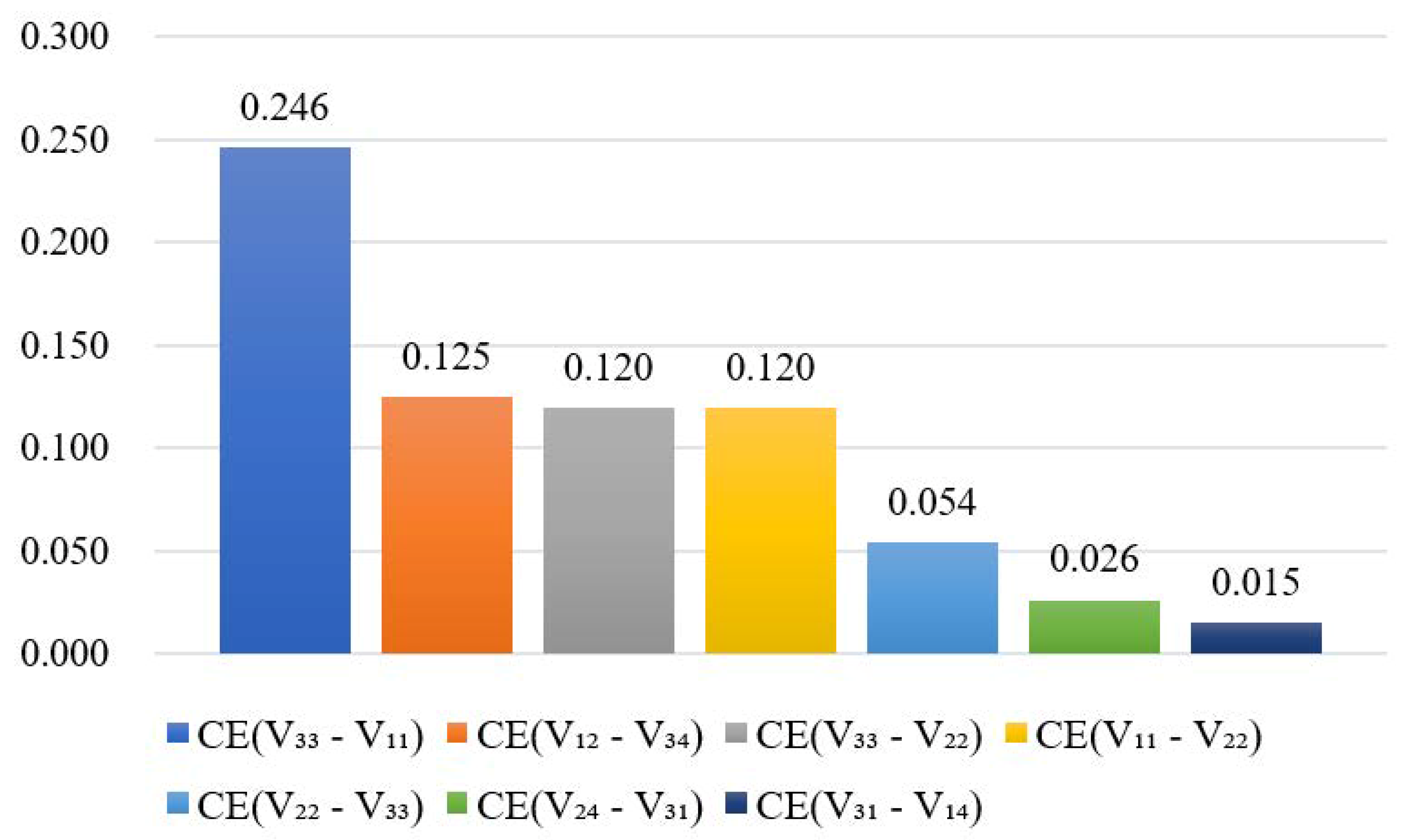
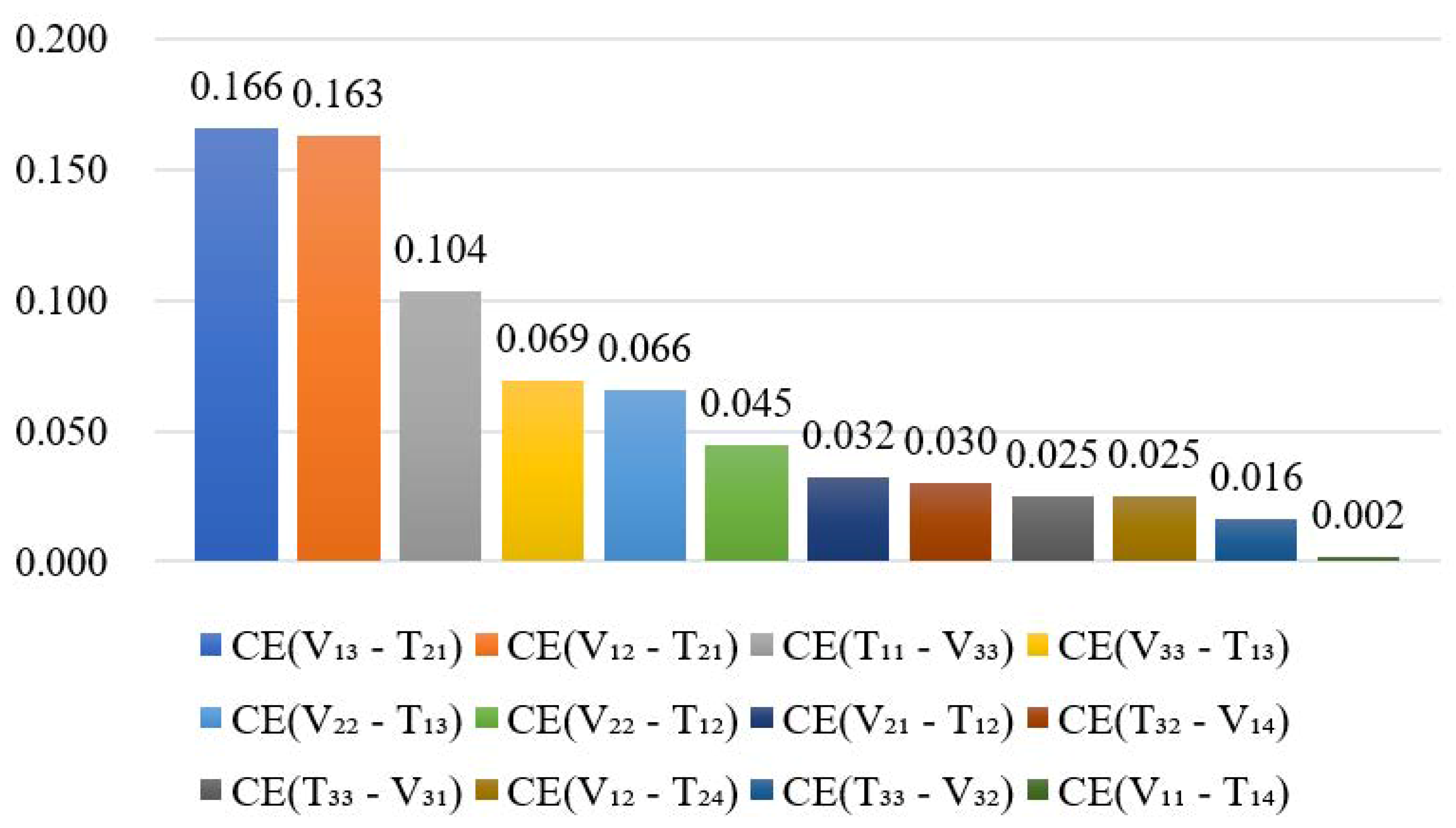
6.3.2. Analysis of Risk Coupling Effects
7. Conclusions and Future
- The risks of HSR projects were comprehensively identified and a multi-layer risk list was determined. Twenty-four risk factors were identified and classified into vulnerability and threatening risk subsystems and six risk categories.
- Coupled risk relationships, which are essentially causal relationships between risk factors, were analysed qualitatively. The results show that there are homogeneous and heterogeneous risk couplings within and between the vulnerability and threatening risk subsystems. This means that risk transmission within and between systems may increase the risk of a certain category or change the risk categories. A mathematical model based on SD was established that quantitatively expresses the risk-increasing effects of the risk coupling relationships on the project’s risk level (risk coupling effects).
- The model was then applied to the ZW HSR project. The results show that, at the end of the next third year: (1) the ZW HSR project has a level III risk rating with high vulnerability risk, of which management risk and capital risk are relatively high; (2) homogeneous vulnerability risk coupling, heterogeneous vulnerability risk coupling and heterogeneous vulnerability-threatening risk coupling contribute most to the total risk of the ZW HSR project, of which V31-V33, V33-V11, V13-T21, and V12-T21 are the key risk pairs. Brief risk mitigation strategies were proposed for these.
Author Contributions
Funding
Conflicts of Interest
References
- Lawrence, M.; Bullock, R.; Liu, Z.M. China’s High-Speed Rail Development; World Bank Publications: Washington, DC, USA, 2019. [Google Scholar]
- Belal, E.M.; Khalil, A.A.; El-Dash, K.M. Economic investigation for building a high-speed rail in developing countries: The case of Egypt. Ain Shams Eng. J. 2020, 2, 003. [Google Scholar] [CrossRef]
- Zhang, H.; Pu, H.; Schonfeld, P.; Song, T.; Li, W.; Wang, J.; Peng, X.B.; Hu, J.P. Multi-objective railway alignment optimization considering costs and environmental impacts. Appl. Soft Comput. 2020, 89, 106105. [Google Scholar] [CrossRef]
- Kabir, G.; Sadiq, R.; Tesfamariam, S. A review of multi-criteria decision-making methods for infrastructure management. Struct. Infrastruct. Eng. 2014, 10, 1176–1210. [Google Scholar] [CrossRef]
- Beijing-Shanghai High Speed Railway Co., Ltd. Beijing-Shanghai High-Speed Railway Standardization Construction Management Manual: Management System Standardization; Beijing-Shanghai High Speed Railway Co., Ltd.: Beijing, China, 2009. [Google Scholar]
- Chang, Y.Z.; Yang, Y.; Dong, S.C. Comprehensive Sustainability Evaluation of High-Speed Railway (HSR) Construction Projects Based on Unascertained Measure and Analytic Hierarchy Process. Sustainability 2018, 10, 408. [Google Scholar] [CrossRef] [Green Version]
- Chandra, H.P. Structural Equation Model for Investigating Risk Factors Affecting Project Success in Surabaya. Procedia Eng. 2015, 125, 53–59. [Google Scholar] [CrossRef] [Green Version]
- Xiang, P.C.; Xie, L.L.; Wang, L.; Zhao, Y.L. Discussion on Engineering Project Integrated Risk Management. Constr. Econ. 2008, 5, 37–39. [Google Scholar]
- David, B. The concept of project complexity—A review. Int. J. Proj. Manag. 1996, 4, 201–204. [Google Scholar] [CrossRef] [Green Version]
- Matthew, H.; Behzad, E.; Paul, C. Safety risk interactions among highway construction work tasks. Constr. Manag. Econ. 2011, 29, 417–429. [Google Scholar] [CrossRef]
- Mattsson, L.G.; Jenelius, E. Vulnerability and resilience of transport systems—A discussion of recent research. Transport. Res. Part A Policy Pract. 2015, 81, 16–34. [Google Scholar] [CrossRef]
- Chapman, R.J. A framework for examining the dimensions and characteristics of complexity inherent within rail megaprojects. Int. J. Proj. Manag. 2016, 34, 937–956. [Google Scholar] [CrossRef]
- Dong, S.C.; Yang, Y.; Li, Y.J.; Cheng, H.; Li, J.N.; Bilgaev, A.; Li, Z.H.; Li, Y. An evaluation of the economic, social, and ecological risks of China-Mongolia-Russia high-speed railway construction and policy suggestions. J. Geogr. Sci. 2018, 28, 900–918. [Google Scholar] [CrossRef] [Green Version]
- Wang, T.; Wang, S.; Zhang, L.M.; Huang, Z.Y.; Li, Y.L. A major infrastructure risk-assessment framework: Application to a cross-sea route project in China. Int. J. Proj. Manag. 2016, 34, 1403–1415. [Google Scholar] [CrossRef]
- Geraldi, J.; Maylor, H.; Williams, T. Now, let’s make it really complex (complicated). Int. J. Oper. Prod. Manag. 2011, 31, 966–990. [Google Scholar] [CrossRef]
- Xiang, P.C.; Liu, D. Analysis on relationship among risks of high-speed railway project based on ISM. World Sci. Tech. R D 2016, 38, 409–414. [Google Scholar]
- Marie, F.; Vidal, L.A.; Bocquet, J.C. Interactions-based risk clustering methodologies and algorithms for complex project management. Int. J. Prod. Econ. 2013, 142, 225–234. [Google Scholar] [CrossRef]
- Coupling. Available online: https://baike.baidu.com/item/%E8%80%A6%E5%90%88/2821124?fr=aladdin (accessed on 21 May 2020).
- Haimes, Y.Y. On the definition of vulnerabilities in measuring risks to infrastructures. Risk Anal. 2006, 26, 293–296. [Google Scholar] [CrossRef]
- Wang, Z.R.; Li, Q.M.; Liang, Z.L. Evaluation of Urban Metro Network Topological Structure Vulnerability. China Saf. Sci. J. 2013, 8, 114–119. [Google Scholar]
- Chang, T.Y.; Deng, X.P.; Ji, Y.G. Research on the Relationship between the Vulnerability and Political Risk of International Construction Projects. J. Beijing Inst. Technol. 2017, 19, 50–56. [Google Scholar]
- Qiao, Y.L. Research on Risk Management of PPP Financing in High-Speed Railways in China. Master’s Thesis, Zhejiang University, Zhejiang, China, 27 August 2011. [Google Scholar]
- Aleksander, P. The challenge of developing high-speed rail projects: Recent evidence from developing countries. Int. J. Geomate 2020, 18, 99–105. [Google Scholar] [CrossRef]
- Lu, L. Debt risk research of local government platform under the new urbanization background. J. Cent. Univ. Financ. Econ. 2013, 9, 14–18. [Google Scholar]
- Locatelli, G.; Mariani, G.; Sainati, T.; Greco, M. Corruption in public projects and megaprojects: There is an elephant in the room! Int. J. Proj. Manag. 2017, 35, 252–268. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.L.; Li, H.C. Comparison of Ticket Price and Passenger Volume between China and Foreign Countries. Railw. Econ. Res. 2016, 5, 37–41. [Google Scholar]
- Lu, C.F. The Establishment and Practice of the “Six in One” Target Control System for Railway Construction Management. Manag. World 2008, 4, 1–7. [Google Scholar]
- Rocha, J.M.; Henriques, A.A.; Calcada, R. Probabilistic assessment of the train running safety on a short-span high-speed railway bridge. Struct. Infrastruct. Eng. 2015, 12, 78–92. [Google Scholar] [CrossRef]
- Mato, F.M.; Cornejo, M.O.; Sánchez, R.A.E. Viaduct over Ulla River in the Atlantic high speed railway line: A composite (steel–concrete) truss world record. Hormigón Acero 2015, 66, 1–25. [Google Scholar] [CrossRef]
- Park, J.; Park, B.; Cha, Y.; Hyun, C. Risk factors assessment considering change degree for mega-projects. Procedia Soc. Behav. Sci. 2016, 218, 50–55. [Google Scholar] [CrossRef] [Green Version]
- Xiang, P.C.; Chang, W. Risk Factors Identification in Interregional Major Engineering Projects Based on HHM. World Sci.-Tech. R D 2015, 37, 67–72. [Google Scholar]
- Guirao, B.; Campa, J.L. The construction of a HSR network using a ranking methodology to prioritise corridors. Land Use Policy 2014, 38, 290–299. [Google Scholar] [CrossRef]
- Xue, Y.T.; Xiang, P.C. The Social Risk of High-speed Rail Projects in China: A Bayesian Network Analysis. Sustainability 2020, 12, 2087. [Google Scholar] [CrossRef] [Green Version]
- Francesca, P.; Irina, D.R. How public participation could improve public decisions on rail investments? Reg. Sci. Policy Pract. 2018, 10, 383–403. [Google Scholar] [CrossRef]
- Qazi, A.; Quigley, J.; Dickson, A.; Kirytopoulosc, K. Project Complexity and Risk Management (ProCRiM): Towards modelling project complexity driven risk paths in construction projects. Int. J. Proj. Manag. 2016, 34, 1183–1198. [Google Scholar] [CrossRef] [Green Version]
- Xiang, P.C.; Zou, L. The organizational operation mechanism of cross region public engineering projects. Sci. Technol. Prog. Policy 2012, 29, 26–29. [Google Scholar]
- Yang, C.X.; Zhang, Z.F. An Assessment Model for R&D Project Risk Conduction Based on Probability Influence Diagram. China Saf. Sci. J. 2011, 21, 118–123. [Google Scholar]
- Zhou, G.H.; Peng, B. Analysis of Quality Management Risk in Large Construction Projects Based on Bayesian Belief Network—A Case Study of Beijing Shanghai High Speed Railway Project. China Soft Sci. 2009, 9, 99–106. [Google Scholar]
- Xiang, P.C.; Liu, Y.L. Research on Risk Coupling Mechanism of Cross-regional Mega Construction Projects. Constr. Econ. 2018, 7, 97–101. [Google Scholar]
- Huang, W. Ecological Risk Assessment of High-Speed Railway Project and Countermeasure: Taking the Zheng-Wan G-Series High-Speed Train as an Example. Master’s Thesis, Chongqing University, Chongqing, China, 27 May 2018. [Google Scholar]
- Jiang, X.; Zhu, P.W.; Shen, L. Risk assessment of resource conflict in hydropower engineering programmes based on both ANP and cloud model. China Saf. Sci. J. 2014, 24, 152–158. [Google Scholar]
- Sanchis, I.V.; Franco, R.I.; Fernández, P.M.; Zuriaga, P.S.; Torres, J.B.F. Risk of increasing temperature due to climate change on high-speed rail network in spain. Transp. Res. Part D Transp. Environ. 2020, 82, 102312. [Google Scholar] [CrossRef]
- Duddeck, H.; Stading, A. Tunnelling in soft ground and sedimentary rock for high-speed double-track railway lines in germany. Tunn. Undergr. Space Technol. 1990, 5, 257–263. [Google Scholar] [CrossRef]
- Huang, D. Study on Environmental Protection Route Selection and Protection of Ming Emperor Mausoleum in Fengyang Section of Beijing-Shanghai High-Speed Railway. In Proceedings of the Annual Conference of Chinese Society for Environmental Sciences, Shanghai, China, 5–7 May 2010; pp. 663–666. [Google Scholar]
- Wang, K.; Xia, W.; Zhang, A. Should china further expand its high-speed rail network? consider the low-cost carrier factor. Transp. Res. Part A 2017, 4, 105–120. [Google Scholar] [CrossRef]
- Albalate, D.; Bel, G. The Economics and Politics of High Speed Rail: Lessons from Experiences Abroad; Lexington Books: Lanham, MD, USA, 2012. [Google Scholar]
- Qin, Y. ‘No county left behind?’ The distributional impact of high-speed rail upgrades in China. J. Econ. Geogr. 2017, 17, 489–520. [Google Scholar] [CrossRef] [Green Version]
- Christiaan, B.; Eric, P. Intermodal competition in the London–Paris passenger market: High-Speed Rail and air transport. J. Urban Econ. 2012, 71, 278–288. [Google Scholar] [CrossRef] [Green Version]
- Stewart, M.G. Life-safety risks and optimisation of protective measures against terrorist threats to infrastructure. Struct. Infrastruct. Eng. 2011, 7, 431–440. [Google Scholar] [CrossRef]
- Li, C.X.; Xi, Z.L. Social Stability Risk Assessment of Land Expropriation: Lessons from the Chinese Case. Int. J. Environ. Res. Public Health 2019, 16, 3952. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, T.; Shen, Q.P.G.; Shi, Q.; Lai, X.D.; Li, Z.D.C.; Xu, K.X. Managing social risks at the housing demolition stage of urban redevelopment projects: A stakeholder-oriented study using social network analysis. Int. J. Proj. Manag. 2017, 35, 925–941. [Google Scholar] [CrossRef]
- He, Z.; Huang, D.; Zhang, C.; Fang, J. Toward a Stakeholder Perspective on Social Stability Risk of Large Hydraulic Engineering Projects in China: A Social Network Analysis. Sustainability 2018, 10, 1223. [Google Scholar] [CrossRef] [Green Version]
- Marincioni, F.; Appiotti, F. The Lyon-Turin High-Speed Rail: The Public Debate and Perception of Environmental Risk in Susa Valley, Italy. Environ. Manag. 2009, 43, 863–875. [Google Scholar] [CrossRef]
- Vyas, G.S.; Jha, K.N.; Patel, D.A. Development of Green Building Rating System Using AHP and Fuzzy Integrals: A Case of India. J. Archit. Eng. 2019, 2, 04019004. [Google Scholar] [CrossRef]
- Li, T.H.Y.; Ng, S.T.; Skitmore, M. Evaluating stakeholder satisfaction during public participation in major infrastructure and construction projects: A fuzzy approach. Autom. Constr. 2013, 29, 123–135. [Google Scholar] [CrossRef]
- Thomas, A.V.; Kalidindi, S.N.; Ganesh, L.S. Modelling and assessment of critical risks in BOT road projects. Constr. Manag. Econ. 2006, 24, 407–424. [Google Scholar] [CrossRef]
- Sadeghi, N.; Fayek, A.R.; Pedrycz, W. Fuzzy monte carlo simulation and risk assessment in construction. Comput. Civ. Infrastruct. Eng. 2010, 25, 238–252. [Google Scholar] [CrossRef]
- Luu, V.T.; Kim, S.Y.; Tuan, N.V.; Ogunlana, S.O. Quantifying schedule risk in construction projects using Bayesian belief networks. Int. J. Proj. Manag. 2009, 27, 39–50. [Google Scholar] [CrossRef]
- Chen, Z.; Boateng, P.; Ogunlana, S.O. A dynamic system approach to risk analysis for megaproject delivery. Proc. Inst. Civ. Eng. Manag. Procure. Law 2019, 172, 232–252. [Google Scholar] [CrossRef]
- Jalal, M.P.; Shoar, S. A hybrid framework to model factors affecting construction labour productivity: Case study of Iran. J. Financial Manag. Prop. Constr. 2018, 24, 630–654. [Google Scholar] [CrossRef]
- Wu, X.G.; Wu, K.B.; Shen, M.F.; Chen, Y.Q.; Zhang, L.M. Research on coupling of safety risks in metro construction based on N-K model. China Saf. Sci. J. 2016, 4, 96–101. [Google Scholar]
- Miller, R.; Lessard, D.R. The Strategic Management of Large Engineering Projects; MIT Press: Cambridge, UK, 2000. [Google Scholar]
- Liu, M.; Le, Y.; Hu, Y.; Xia, B.; Gao, X. System dynamics modeling for construction management research: Critical review and future trends. J. Civ. Eng. Manag. 2019, 25, 730–741. [Google Scholar] [CrossRef] [Green Version]
- Wang, F.; Ding, L.; Love, P.E.; Edwards, D.J. Modeling tunnel construction risk dynamics: Addressing the production versus protection problem. Saf. Sci. 2016, 87, 101–115. [Google Scholar] [CrossRef]
- Nasirzadeh, F.; Afshar, A.; Khanzadi, M.; Howick, S. Integrating system dynamics and fuzzy logic modelling for construction risk management. Constr. Manag. Econ. 2008, 26, 1197–1212. [Google Scholar] [CrossRef]
- Yu, L.L.; Li, S.C.; Sun, H.L. Effects of Tunnel Project on Ecological Environment and Ecological Strategies. Bull. Soil Water Conserv. 2010, 30, 233–237. [Google Scholar]
- Yang, T.; Wang, N.M. An Empirical Study on the Coupling Model of Ecological Environment and Urban Competitiveness. Ecol. Econ. 2008, 10, 33–36. [Google Scholar]
- Liu, C.L. Common Mistakes in Coupling Degree Calculation. J. Huaiyin Teach. Coll. 2017, 16, 18–22. [Google Scholar]
- Jin, L.; Chang, Y.; Ju, X.; Xu, F. A Study on the Sustainable Development of Water, Energy, and Food in China. Int. J. Environ. Res. Public Health 2019, 16, 3688. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Environmental Impact Assessment of Zhengzhou-Wanzhou Railway. Available online: http://www.lddoc.cn/p-63712.html (accessed on 2 January 2018).
- Zhao, P.; Liu, K.; Li, X.D. Quantitative Analysis of On-site Safety Management of Construction Enterprises Based on the MM. Saf. Environ. Eng. 2017, 24, 134–140. [Google Scholar]

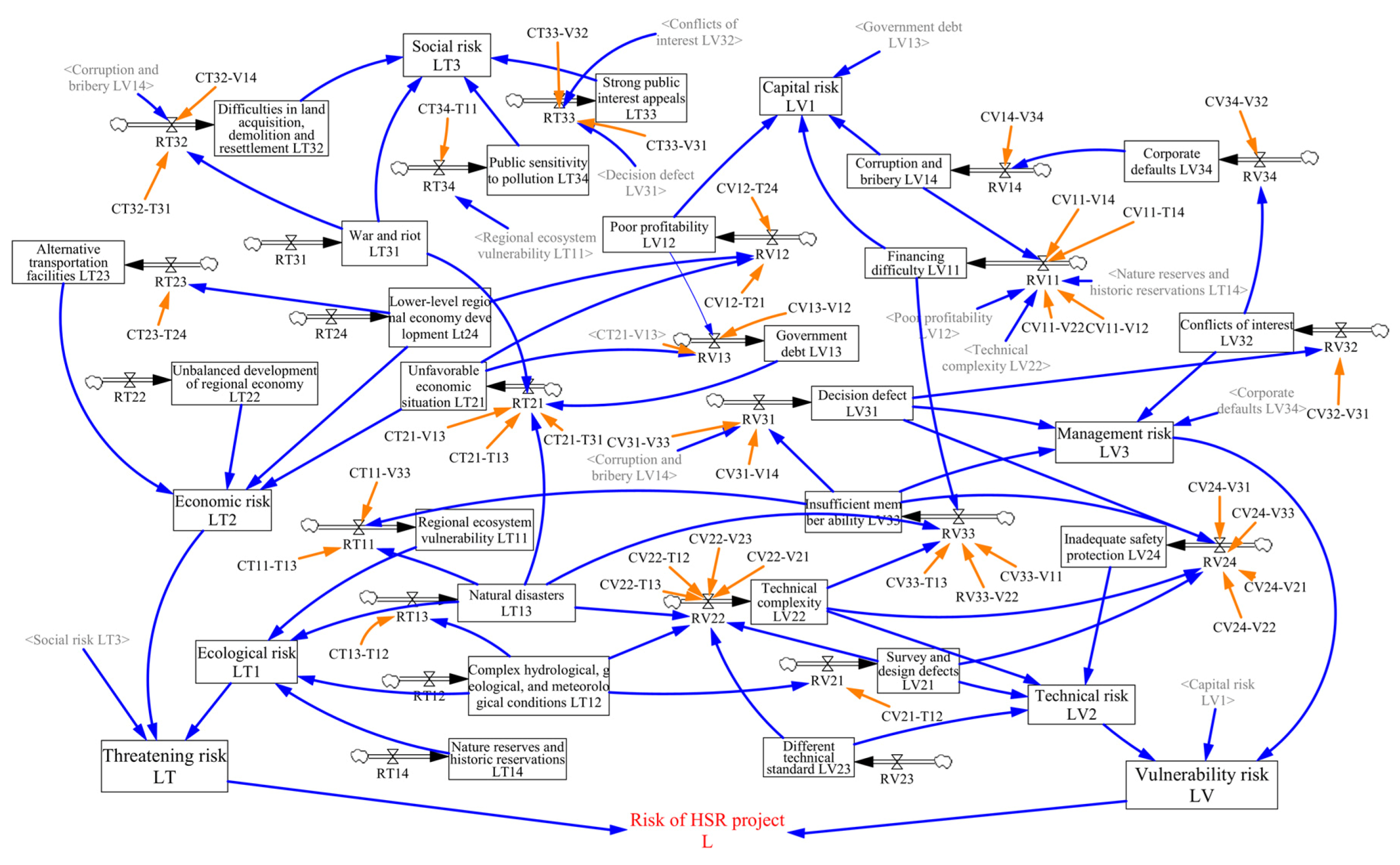


| Risk Subsystems | Risk Categories | Risk Factors |
|---|---|---|
| Vulnerability | Capital risk | Financing difficulty Poor profitability Government debt Corruption and bribery |
| Technical risk | Survey and design defects Technical complexity Different technical standard Inadequate safety protection | |
| Management risk | Decision defect Conflicts of interest Insufficient member ability Corporate defaults | |
| Threatening | Ecological risk | Regional ecosystem vulnerability Complex hydrological, geological, and meteorological conditions Natural disasters Nature reserves and historic reservations |
| Economic risk | Unfavorable economic situation Unbalanced development of regional economy ; Alternative transportation facilities Lower-level regional economy development | |
| Social risk | War and riot Difficulties in land acquisition, demolition and resettlement | |
| Strong public interest appeals Public sensitivity to pollution |
| Reference | Method | Features and Advantages | Limitations |
|---|---|---|---|
| [14,54] | Analytic hierarchy process | The comprehensive importance of each level factor can be obtained, making it suitable for decision-making in complex systems with multiple objectives, levels and factors. | The data is subjective and not always convincing enough, and new decision-making options are not available. |
| [55] | Fuzzy comprehensive evaluation | Based on the theory of fuzzy mathematics, multi-layer operations are run to determine the risk level of the project. It is suitable for the evaluation of fuzzy or qualitative risks. | The determination of factor weights is subjective and not convincing enough. |
| [56] | Delphi | Semi-structured questionnaires on risk are sent to a group of experts for multiple rounds until a reliable consensus is reached. Used for problems that are difficult to handle by other methods. | The results depend largely on the experts’ qualifications and number. |
| [57] | Monte Carlo simulation | A risk structure is established and the mathematical relationships between risk variables are expressed by a Bayesian formula. Applicable to problems with obvious causality between risks. | Large amounts of high-quality data are required to obtain a convincing risk structure and conditional risk probability distributions. |
| [58] | Bayesian network | The risk structure is established and the mathematical relationship between risk variables is expressed by Bayesian formula. It is applicable to the problems with obvious causality between risks. | Large amounts and high-quality data are required to obtain a convincing risk structure and conditional probability distributions of risks. |
| [17] | Interpretative structural modeling | An adjacency matrix is used to study the interactions between risks and establish a risk structure. Risks can be divided into several categories according to the type and intensity of their interactions. | Only suitable for qualitative risk analysis. Quantitative evaluations cannot be obtained. |
| [59,60] | System dynamics | A complex system with multiple variables and nonlinear characteristics can be constructed and predicted dynamically, and the interactions of the system’s components can be represented quantitatively. | It is difficult to construct a suitable dynamic model of a complex system. |
| [61] | N-K model | The current status of a complex system and the effects of the interactions between different components can be analyzed quantitatively. | A large amount of complete historical data is required, and the future situation cannot be predicted. |
| Case Description | Causal Relationship of Risk Factors | Direction of Risk Coupling |
|---|---|---|
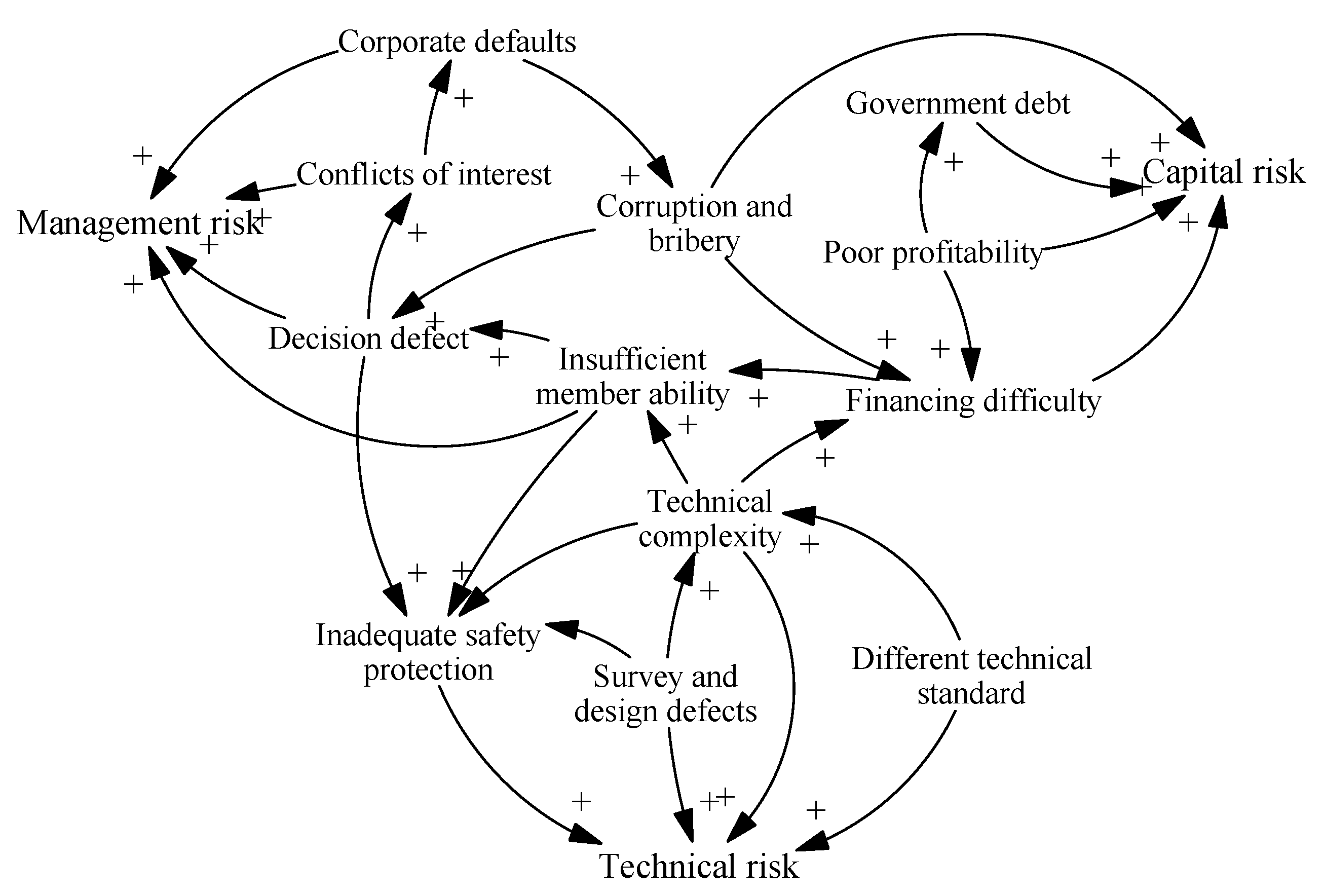
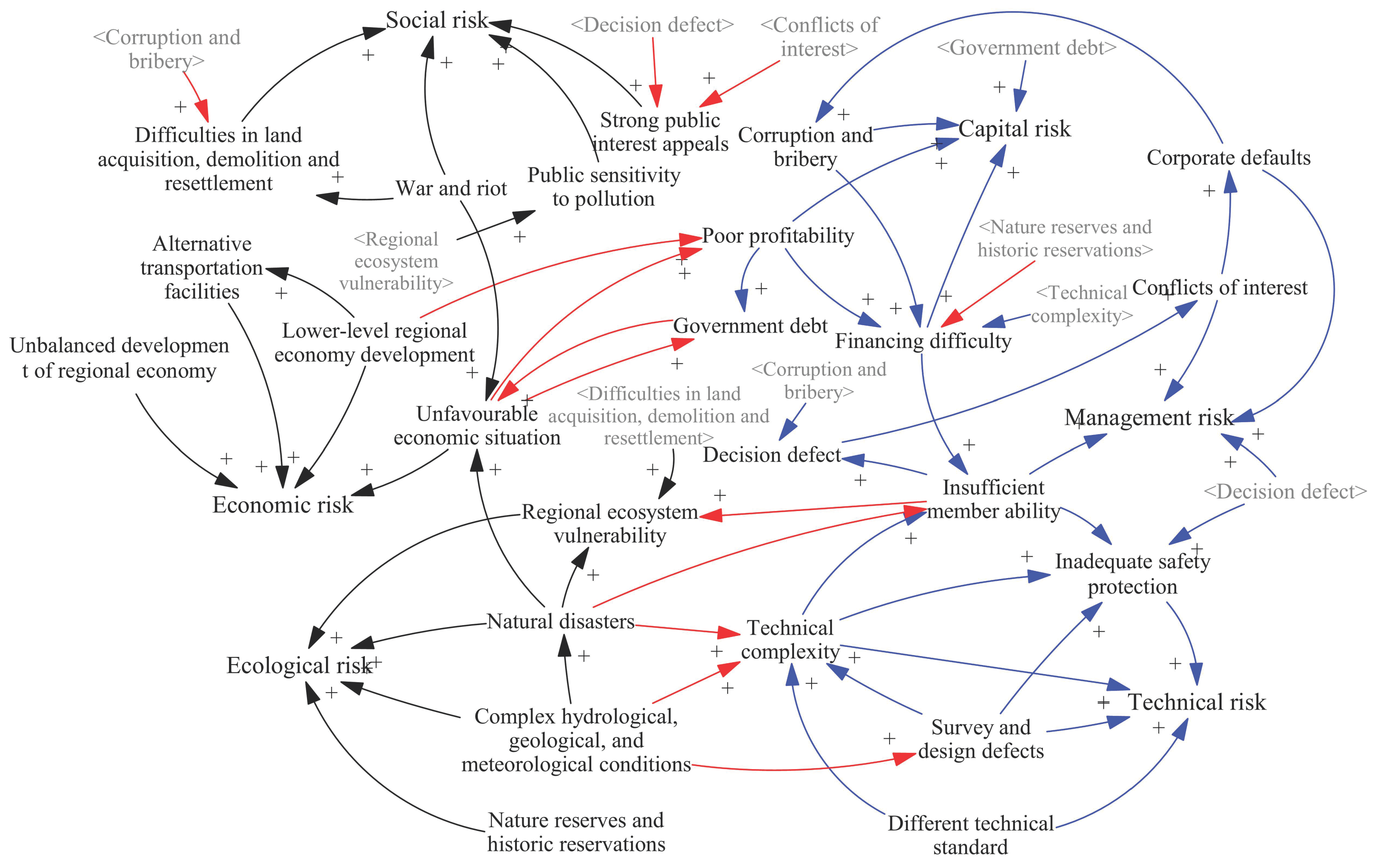
| Beijing-Shanghai high-speed rail (HSR) passes through the Ming Mausoleum (a key national heritage conservation unit) and crosses Yangcheng Lake Ecological Area (an ecological protection zone). In order to defend the integrity of the sites and reduce water pollution, the original design and construction scheme of the project has been modified. The new scheme increased the length of the bridge by 5931 m and the main engineering cost increased by 29.02 million yuan. The major changes to the project have caused great financial stress for its investors. | Nature reserves and historic reservation → Financing difficulty | Ecological risk → Capital risk |
| During the construction of the Beijing-Shanghai HSR, costs increased significantly due to high inflation. Owing to the large amount of project loans, long construction period and rising interest rate, the debt burdens of the Ministry of Railways and of local governments increased. For example, 80.8% of the lines have used viaduct technology, for which the cost per km is 20–30 million yuan higher than that of ordinary subgrade. Half of this investment is financed by bank loans. Even if the minimum interest rate of syndicated loans at that time was 5.5%, the annual interest expense would be 6.05 billion yuan. | Unfavorable economic situation → Government debt | Economic risk → Capital risk |
| Poor geological engineering conditions along the Beijing-Shanghai HSR, mainly manifested as soft soil, make its construction difficult. | Complex hydrological, geological, and meteorological conditions → Technical complexity | Ecological risk → Technical risk |
| During the construction of the Beijing-Shanghai HSR, the design institutes did not complete the design work in time according to the environmental impact assessment (EIA) document, which affected the implementation of the environmental protection measures. Additionally, the construction enterprises did not carry out unified treatment of waste soil according to their contracts, instead using it to fill ponds and mountain gullies, thus causing air and water pollution, which is harmful to the local water and soil environments. | Corporate defaults → Regional ecosystem vulnerability | Management risk → Ecological risk |
| Due to a lack of public participation in the HSR planning system during the planning of the Shanghai-Wuhan-Chengdu HSR and Shanghai-Kunming HSR, members of the public spontaneously gathered for demonstrations and caused mass incidents to express their strong appeal for the implementation of HSR transit in their areas. | Decision defect → Strong public interest appeals | Management risk → Social risk |
| During the planning of the Dazhou-Chongqing HSR, there was a dispute between the East Line and West Line, which caused local governments to compete for the project. Among them, the governments of Dazhou and Guang’an made different statements regarding the line chosen for HSR on their information websites, which aroused dissatisfaction and strong appeals from the public. | Conflicts of interest → Strong public interest appeals | Management risk → Social risk |
| Due to the continental plate on which Indonesia is located, earthquakes and volcanic eruptions are frequent. Indonesia’s Ministry of Transport have stressed twice that, if earthquake resistance requirements cannot be met, construction of the Jakarta-Bandung HSR project will not be permitted. Such natural disasters pose challenges to existing design and construction technology. | Natural disasters → Technical complexity | Ecological risk → Technical risk |
| Compensation for land acquired for the Zhengzhou-Xuzhou HSR was embezzled by local officials. Because the compensation did not meet state standards, this hurt the interests of the people and resulted in petitions. | Corruption and bribery → Difficulties in land acquisition, demolition and resettlement | Capital risk → Social risk |
| As local people may lack the capacity and willingness to pay for tickets, only about 30 pairs of HSR Electric Multiple Units (EMUs) of Zhengzhou-Xi’an HSR operates every day, with an attendance rate of less than 50%. After two years’ operation, in 2016, this HSR line lost 1.4 billion yuan, leaving the Zhengzhou Railway Bureau at a loss of 1 billion yuan. | Lower-level regional economy development → Government debt | Economic risk → Capital risk |
| A serious epidemic influenced the macro-economies of various countries. Basic economic activity nearly collapsed and market demand for HSR was almost non-existent. The volume of passenger traffic in the Beijing-Shenyang HSR was less than 10%, and ticket revenue could not support the high operating cost. | Unfavorable economic situation → Poor profitability | Economic risk → Capital risk |
| The Fujian section of the Ganzhou-Longyan HSR is located in the mountains of Northwest Fujian. Carbonate rock and karst are widely distributed, and the erosional surface is dissected deeply by valleys. It is difficult to carry out accurate surveys, resulting in the hidden danger of engineering design defects. | Complex hydrological, geological, and meteorological conditions → Survey and design defects | Ecological risk → Technical risk |
| China Railway Corporation’s financial report shows that, up to September 2018, the company’s debt was 5.28 trillion yuan, which is mainly borne by the Railway Bureau and local governments. Experts have stated that once the debt risk is out of control, it may cause systemic financial risk. | Government debt → Unfavorable economic situation | Capital risk → Economic risk |
| The California HSR project is located on the Pacific Plate, which has high seismic activity. Generally speaking, HSR needs rigid structures to meet strict limits of deflection and vibration control. However, in earthquake areas, flexible and ductile structures are more earthquake-proof, which brings additional challenges to the designers and constructors of this project. | Natural disasters → Insufficient member ability | Ecological risk → Management risk |
| Target Layer Indicator (L) | Standard Layer Indicators ( ) | Field Layer Indicators ( ) | Index Layer Indicators ( ) | Mean Value () |
Absolute Weights of
() | Relative Weights of () |
|---|---|---|---|---|---|---|
| Risk of HSR project | Vulnerability risk = 0.553 | Capitalrisk risk V1 = 0.374 | Financing difficulty | 4.125 | 0.055 | 0.266 |
| Poor profitability | 3.267 | 0.044 | 0.212 | |||
| Government debt | 3.625 | 0.049 | 0.237 | |||
| Corruption and bribery | 4.400 | 0.059 | 0.285 | |||
| Technical risk = 0.325 | Survey and design defects | 4.400 | 0.059 | 0.328 | ||
| Technical complexity | 3.500 | 0.047 | 0.261 | |||
| Different technical standard | 3.267 | 0.044 | 0.244 | |||
| Inadequate safety protection | 2.215 | 0.030 | 0.167 | |||
| Management risk = 0.301 | Decision defect | 3.625 | 0.049 | 0.295 | ||
| Conflicts of interest | 3.375 | 0.045 | 0.271 | |||
| Insufficient member ability | 2.250 | 0.030 | 0.181 | |||
| Corporate defaults | 3.125 | 0.042 | 0.253 | |||
| Threatening risk = 0.447 | Ecological risk = 0.326 | Regional ecosystem vulnerability | 3.533 | 0.047 | 0.324 | |
| Complex hydrological, geological, and meteorological conditions | 3.067 | 0.041 | 0.283 | |||
| Natural disasters | 2.375 | 0.032 | 0.221 | |||
| Nature reserves and historic reservations | 1.875 | 0.025 | 0.172 | |||
| Economic risk = 0.342 | Unfavorable economic situation | 3.667 | 0.049 | 0.32 | ||
| Unbalanced development of regional economy | 2.375 | 0.032 | 0.209 | |||
| Alternative transportation facilities | 2.215 | 0.030 | 0.196 | |||
| Lower-level regional economy development | 3.133 | 0.042 | 0.275 | |||
| Social risk = 0.332 | War and riot | 2.533 | 0.034 | 0.228 | ||
| Difficulties in land acquisition, demolition and resettlement | 4.000 | 0.054 | 0.362 | |||
| Strong public interest appeals | 1.750 | 0.024 | 0.161 | |||
| Public sensitivity to pollution | 2.750 | 0.037 | 0.249 |
| Risk Value | 0.1 | 0.3 | 0.5 | 0.7 | 0.9 |
|---|---|---|---|---|---|
| Degree of impact | Negligible | Low | Medium | Serious | Very serious |
| Risk Factor | Risk Value | Risk Factor | Risk Value |
|---|---|---|---|
| Financing difficulty | 0.77 | Regional ecosystem vulnerability | 0.64 |
| Poor profitability | 0.75 | Complex hydrological, geological, and meteorological conditions | 0.76 |
| Government debt | 0.67 | Natural disasters | 0.54 |
| Corruption and bribery | 0.67 | Nature reserves and historic reservations | 0.23 |
| Survey and design defects | 0.60 | Unfavorable economic situation | 0.45 |
| Technical complexity | 0.90 | Unbalanced development of regional economy | 0.31 |
| Different technical standard | 0.19 | Alternative transportation facilities | 0.29 |
| Inadequate safety protection | 0.42 | Lower-level regional economy development | 0.41 |
| Decision defect | 0.79 | War and riot | 0.26 |
| Conflicts of interest | 0.84 | Difficulties in land acquisition, demolition and resettlement | 0.51 |
| Insufficient member ability | 0.60 | Strong public interest appeals | 0.48 |
| Corporate defaults | 0.85 | Public sensitivity to pollution | 0.35 |
| Coupled Risk Factors | Coupling Coefficient | Coupled Risk Factors | Coupling Coefficient |
|---|---|---|---|
| CV11-V14 | 0.976 | CV31-V33 | 0.910 |
| CV11-T14 | 0.178 | CV31-V14 | 0.166 |
| CV11-V22 | 0.966 | CV32-V31 | 0.995 |
| CV11-V12 | 0.999 | CV33-V11 | 0.925 |
| CV12-T24 | 0.428 | CV33-V22 | 0.806 |
| CV12-T21 | 0.940 | CV33-T13 | 0.986 |
| CV13-V12 | 0.984 | CV34-V32 | 0.839 |
| CV13-T21 | 0.821 | CT11-V33 | 0.794 |
| CV14-V34 | 0.932 | CT11-T13 | 0.965 |
| CV21-T12 | 0.933 | CT13-T12 | 0.865 |
| CV22-V23 | 0.061 | CT21-V13 | 0.821 |
| CV22-V21 | 0.806 | CT21-T13 | 0.959 |
| CV22-T12 | 0.960 | CT23-T24 | 0.861 |
| CV22-T13 | 0.714 | CT32-T31 | 0.573 |
| CV24-V21 | 0.854 | CT32-V14 | 0.911 |
| CV24-V22 | 0.482 | CT33-V31 | 0.736 |
| CV24-V31 | 0.612 | CT34-T11 | 0.639 |
| CV24-V33 | 0.854 | CT21-T31 | 0.690 |
| CT33-V32 | 0.679 | - | - |
| Risk Rating | Interval of Risk Level | Specified Interval Value of Risk Level | Risk Management Principle |
|---|---|---|---|
| V | (0, 20%) | (3.75, 9.55) | There are acceptable minor risks and the project can be carried out normally |
| IV | (20%, 40%) | (9.55, 15.36) | There are general risks that should be attended to |
| III | (40%, 60%) | (15.36, 21.16) | There are obvious risks and mitigation measures should be taken |
| II | (60%, 80%) | (21.16, 26.96) | The project is highly risky and needs to be modified immediately |
| I | (80%, 100%) | (26.96, 32.7) | The project is extremely risky and needs to be suspended, with risk control measures implemented immediately |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, Y.; Xiang, P.; Jia, F.; Liu, Z. Risk Assessment of High-Speed Rail Projects: A Risk Coupling Model Based on System Dynamics. Int. J. Environ. Res. Public Health 2020, 17, 5307. https://0-doi-org.brum.beds.ac.uk/10.3390/ijerph17155307
Xue Y, Xiang P, Jia F, Liu Z. Risk Assessment of High-Speed Rail Projects: A Risk Coupling Model Based on System Dynamics. International Journal of Environmental Research and Public Health. 2020; 17(15):5307. https://0-doi-org.brum.beds.ac.uk/10.3390/ijerph17155307
Chicago/Turabian StyleXue, Yutong, Pengcheng Xiang, Fuyuan Jia, and Zhaowen Liu. 2020. "Risk Assessment of High-Speed Rail Projects: A Risk Coupling Model Based on System Dynamics" International Journal of Environmental Research and Public Health 17, no. 15: 5307. https://0-doi-org.brum.beds.ac.uk/10.3390/ijerph17155307






