A Dynamic Spatio-Temporal Analysis of Urban Expansion and Pollutant Emissions in Fujian Province
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Pollutant Emissions Data
2.3. Remote Sensing Data
2.4. Geographical Factors
2.5. Statistical Modeling
3. Results
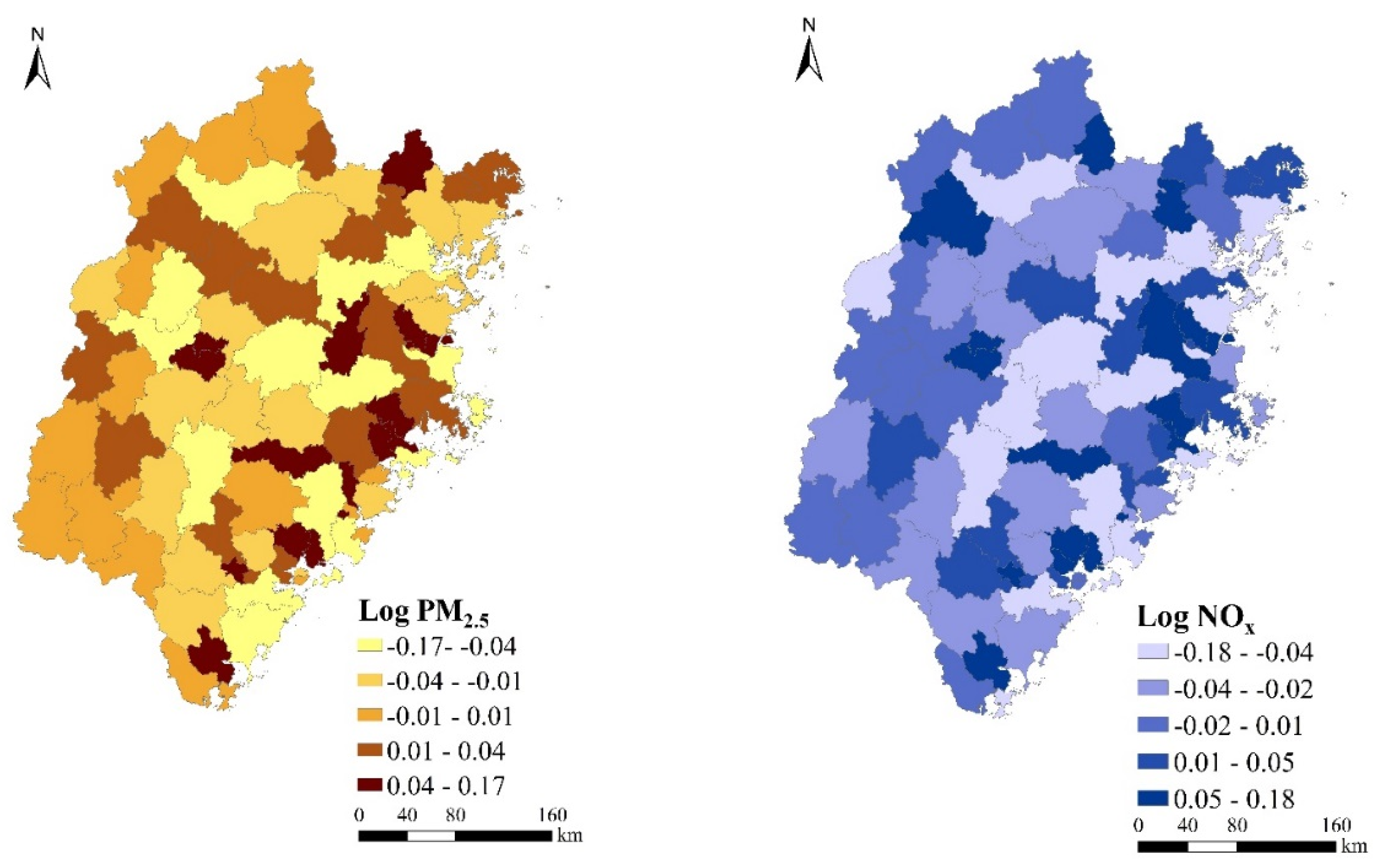
3.1. Spatio-Temporal Dynamics of Pollutant Emissions and Urban Expansion
3.2. Model Estimation Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Patel, R.B.; Burke, T.F. Urbanization—An emerging humanitarian disaster. N. Engl. J. Med. 2009, 361, 741–743. [Google Scholar] [CrossRef] [Green Version]
- UN DESA’s. The 2014 Revision of the World Urbanization Prospects by UN DESA’s Population Division. 2014. Available online: https://www.un.org/development/desa/publications/2014-revision-world-urbanization-prospects.html (accessed on 17 January 2020).
- Zhu, Y.G.; Ioannidis, J.P.A.; Li, H.; Jones, K.C.; Martin, F.L. Understanding and harnessing the health effects of rapid urbanization in China. Environ. Sci. Technol. 2011, 45, 5099–5104. [Google Scholar] [CrossRef] [PubMed]
- Gong, P.; Liang, S.; Carlton, E.J.; Jiang, Q.W.; Wu, J.Y.; Wang, L.; Remais, J.V. Urbanization and health in China. Lancet 2012, 379, 843–852. [Google Scholar] [CrossRef]
- Valverde, V.; Pay, M.T.; Baldasano, J.M. A model-based analysis of SO2 and NO2 dynamics from coal-fired power plants under representative synoptic circulation types over the Iberian Peninsula. Sci. Total Environ. 2016, 541, 701–713. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lai, H.C.; Ma, H.W.; Chen, C.R.; Hsiao, M.C.; Pan, B.H. Design and application of a hybrid assessment of air quality models for the source apportionment of PM2.5. Atmos. Environ. 2019, 212, 116–127. [Google Scholar] [CrossRef]
- Lu, X.C.; Lin, C.Q.; Li, W.K.; Chen, Y.; Huang, Y.Q.; Fung, J.C.H.; Lau, A.K. Analysis of the adverse health effects of PM2.5 from 2001 to 2017 in China and the role of urbanization in aggravating the health burden. Sci. Total Environ. 2019, 652, 683–695. [Google Scholar] [CrossRef]
- Schiavon, M.; Redivo, M.; Antonacci, G. Assessing the air quality impact of nitrogen oxides and benzene from road traffic and domestic heating and the associated cancer risk in an urban area of Verona (Italy). Atmos. Environ. 2015, 120, 234–243. [Google Scholar] [CrossRef]
- Conibear, L.; Butt, E.W.; Knote, C.; Arnold, S.R.; Spracklen, D.V. Stringent Emission Control Policies Can Provide Large Improvements in Air Quality and Public Health in India. Earth Space Sci. 2018. [Google Scholar] [CrossRef]
- Kassomenos, P.; Vardoulakis, S.; Chaloulakou, A.; Grivas, G.; Borge, R.; Lumbreras, J. Levels, sources and seasonality of coarse particles (PM10–PM2.5) in three European capitals–implications for particulate pollution control. Atmos. Environ. 2012, 54, 337–347. [Google Scholar] [CrossRef] [Green Version]
- Landis, M.S.; Patrick, P.J.; Graney, J.R.; White, E.M.; Edgerton, E.S.; Legge, A.; Percy, K.E. Source apportionment of ambient fine and coarse particulate matter at the Fort McKay community site, in the Athabasca Oil Sands region, Alberta, Canada. Sci. Total Environ. 2017, 584–585, 105–117. [Google Scholar] [CrossRef]
- Al-Mulali, U.; Ozturk, I.; Lean, H.H. The influence of economic growth, urbanization, trade openness, financial development, and renewable energy on pollution in Europe. Nat. Hazards 2015, 79, 621–644. [Google Scholar] [CrossRef]
- Li, M.; Li, C.; Zhang, M. Exploring the spatial spillover effects of industrialization and urbanization factors on pollutants emissions in China’s Huang-Huai-Hai region. J. Clean Prod. 2018, 195, 154–162. [Google Scholar] [CrossRef]
- Zhu, Y.J.; Zhan, Y.; Wang, B.; Li, Z.; Qin, Y.Q.; Zhang, K.S. Spatiotemporally mapping of the relationship between NO2 pollution and urbanization for a megacity in Southwest China during 2005–2016. Chemosphere 2019, 220, 155–162. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.C.; Miao, Y.M.; Gao, C.; Long, R.Y.; Chen, H.; Zhao, B.; Wang, S.X. Regional differences in impacts of economic growth and urbanization on air pollutants in China based on provincial panel estimation. J. Clean Prod. 2019, 208, 340–352. [Google Scholar] [CrossRef]
- Haining, R. Spatial Data Analysis: Theory and Practice; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Rushworth, A.; Lee, D.; Mitchell, R. A spatio-temporal model for estimating the long-term effects of air pollution on respiratory hospital admissions in Greater London. Spat. Spatio Temporal Epidemiol. 2014, 10, 29–38. [Google Scholar] [CrossRef] [Green Version]
- Lee, D.; Rushworth, A.; Napier, G. Spatio-temporal areal unit modelling in R with conditional autoregressive priors using the CARBayesST package. J. Stat. Softw. 2018, 84. [Google Scholar] [CrossRef] [Green Version]
- Desmet, K.; Nagy, D.K.; Rossi-Hansberg, E. The Geography of development. J. Political Econ. 2018, 126, 903–983. [Google Scholar] [CrossRef] [Green Version]
- Baklanov, A.; Molina, L.T.; Gauss, M. Megacities, air quality and climate. Atmos. Environ. 2016, 126, 235–249. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhou, Y.; Seto, K.C.; Stokes, E.C.; Deng, C.B.; Pickett, S.T.A.; Taubenböck, H. Understanding an urbanizing planet: Strategic directions for remote sensing. Remote Sens. Environ. 2019, 228, 164–182. [Google Scholar] [CrossRef]
- Huang, Y.; Shen, H.Z.; Chen, H.; Wang, R.; Zhang, Y.Y.; Su, S.; Chen, Y.; Lin, N.; Zhuo, S.; Zhong, Q.; et al. Quantification of global primary emissions of PM2.5, PM10, and TSP from combustion and industrial process sources. Environ. Sci. Technol. 2014, 48, 13834–13843. [Google Scholar] [CrossRef]
- Chen, H.; Huang, Y.; Shen, H.Z.; Chen, Y.L.; Ru, M.Y.; Chen, Y.C.; Lin, N.; Su, S.; Zhuo, S.; Zhong, Q.; et al. Modeling temporal variations in global residential energy consumption. Appl. Energy 2017, 184, 820–829. [Google Scholar] [CrossRef]
- Chen, X.; Nordhaus, W. Using luminosity data as a proxy for economic statistics. Proc. Natl. Acad. Sci. USA 2011, 108, 8589–8594. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- National Bureau of Statistics of China. China’s Total Population and Structural Changes in 2011. Available online: http://www.stats.gov.cn/english/newsandcomingevents/t20120120_402780233.htm (accessed on 29 September 2019).
- Shen, H.Z.; Tao, S.; Chen, Y.; Ciais, P.; Guneralp, B.; Ru, M.Y.; Zhong, Q.; Yun, X.; Zhu, X.; Huang, T.; et al. Urbanization-induced population migration has reduced ambient PM2.5 concentrations in China. Sci. Adv. 2017, 3, e1700300. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fang, D.; Chen, B.; Hubacek, K.; Ni, R.J.; Chen, L.L.; Feng, K.S.; Lin, J. Clean air for some: Unintended spillover effects of regional air pollution policies. Sci. Adv. 2019, 5, eaav4707. [Google Scholar] [CrossRef] [Green Version]
- Lloyd, C.; Catney, G.; Williamson, P.; Bearman, N. Exploring the utility of grids for analysing long term population change. Comput. Environ. Urban Syst. 2017, 66, 1–12. [Google Scholar] [CrossRef]
- Fickas, K.C.; Cohen, W.B.; Yang, Z.Q. Landsat-based monitoring of annual wetland change in the Willamette Valley of Oregon, USA from 1972 to 2012. Wetl. Ecol. Manag. 2016, 24, 73–92. [Google Scholar] [CrossRef]
- Zhou, Y.; Smith, S.J.; Zhao, K.; Imhoff, M.; Thomson, A.; Bond-Lamberty, B.; Asrar, G.R.; Zhang, X.; He, C.; Elvidge, C.D. A global map of urban extent from nightlights. Environ. Res. Lett. 2015. [Google Scholar] [CrossRef]
- Li, X.; Gong, P.; Liang, L. A 30-year (1984–2013) record of annual urban dynamics of Beijing City derived from Landsat data. Remote Sens. Environ. 2015, 166, 78–90. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, X.; Asrar, G.R.; Smith, S.J.; Imhoff, M. A global record of annual urban dynamics (1992–2013) from nighttime lights. Remote Sens. Environ. 2018, 219, 206–220. [Google Scholar] [CrossRef]
- Wang, Q.; Kwan, M.P.; Zhou, K.; Fan, J.; Wang, Y.F.; Zhan, D.S. The impacts of urbanization on fine particulate matter (PM2.5) concentrations: Empirical evidence from 135 countries worldwide. Environ. Pollut. 2019, 247, 989–998. [Google Scholar] [CrossRef]
- Chen, X.; Nordhaus, W. VIIRS nighttime lights in the estimation of cross-sectional and time-series GPS. Remote Sens. 2019, 11, 1057. [Google Scholar] [CrossRef] [Green Version]
- Dang, L.J.; Xu, Y.; Tang, Q. The pattern of available construction land along the Xijiang River in Guangxi, China. Land Use Policy 2015, 42, 102–112. [Google Scholar] [CrossRef]
- Krugman, P. Increasing returns and economic geography. J. Polit. Econ. 1991, 99, 483–499. [Google Scholar] [CrossRef]
- Proost, S.; Thisse, J.F. What can be learned from spatial economics. J. Econ. Lit. 2019, 57, 575–643. [Google Scholar] [CrossRef] [Green Version]
- Rushworth, A.; Lee, D.; Sarran, C. An adaptive spatiotemporal smoothing model for estimating trends and step changes in disease risk. J. R. Stat. Soc. C Appl. 2017, 66, 141–157. [Google Scholar] [CrossRef] [Green Version]
- Rue, H.; Held, L. Gaussian Markov Random Fields: Theory and Applications; Chapman and Hall/CRC: New York, NY, USA, 2005. [Google Scholar]
- Leroux, B.; Lei, X.; Breslow, N. Estimation of disease rates in small areas: A new mixed model for spatial dependence. In Statistical Models in Epidemiology, the Environment, and Clinical Trials; Halloran, M., Berry, D., Eds.; Springer: New York, NY, USA, 1999; pp. 135–178. [Google Scholar]
- Spiegelhalter, D.J.; Best, D.N.; Carlin, B.P.; Linde, A.V.D. Bayesian measures of model complexity and fit (with discussion). J. R. Stat. Soc. B 2002, 64, 583–639. [Google Scholar] [CrossRef] [Green Version]
- Openshaw, S.; Taylor, P.J. A million or so correlation coefficients: Three experiments on the modifiable areal unit problem. In Statistical Applications in the Spatial Sciences; Wrigley, N., Ed.; Pion: London, UK, 1979; pp. 127–144. [Google Scholar]
- Fotheringham, A.S.; Wong, D.W.S. The modifiable areal unit problem in multivariate statistical analysis. Environ. Plan. A 1991, 23, 1025–1044. [Google Scholar] [CrossRef]




| Variables | Description | Mean | Standard Deviation |
|---|---|---|---|
| Log PM2.5 | Log of PM2.5 emission intensity of each county (kg/km2) | 4.49 (1995) | 0.71 |
| 4.59 (2015) | 0.63 | ||
| Log NOx | Log of NOx emission intensity of each county (kg/km2) | 4.66 (1995) | 0.65 |
| 5.00 (2015) | 0.67 | ||
| ULDI | urban land development intensity of each county | 0.080 (1995) | 0.15 |
| 0.128 (2015) | 0.21 | ||
| LD | NTL density of each county | 0.102 (1995) | 0.16 |
| 0.141 (2015) | 0.22 | ||
| Green | Green space density of each county | 0.518 (1995) | 0.89 |
| 0.541 (2015) | 0.65 | ||
| ACLD | Available construction land of each county | 0.076 (1995) | 0.06 |
| 0.067 (2015) | 0.05 | ||
| Dist_City | Log of the distance of each county to its prefecture-level city | 1.518 | 0.60 |
| Coastal | Dummy variable: 1 for coastal county; 0 otherwise | 41.2% | --- |
| Dist_Xiamen | Log of the distance of each county to Xiamen (km) | 2.136 | 0.42 |
| Variables | PM2.5 Model | NOx Model | ||||
|---|---|---|---|---|---|---|
| Median | 2.5% | 97.5% | Median | 2.5% | 97.5% | |
| Intercept | 11.76 * | 8.775 | 13.73 | 11.52 * | 8.908 | 14.37 |
| ULDI | 1.574 * | 1.062 | 1.984 | 1.764 * | 1.215 | 2.155 |
| Green | −0.021 | −0.026 | 0.066 | −0.026 | −0.025 | 0.077 |
| ACLD | 1.448 | −2.191 | 4.705 | 1.079 | −1.72 | 4.502 |
| Coastal | 0.044 | −0.152 | 0.262 | −0.056 | −0.278 | 0.14 |
| Dist_City | −0.163 * | −0.205 | −0.114 | −0.175 * | −0.224 | −0.122 |
| Dist_Xiamen | −0.459 * | −0.658 | −0.196 | −0.485 * | −0.921 | −0.215 |
| τ2 | 0.293 | 0.255 | 0.339 | 0.349 | 0.304 | 0.403 |
| σ2 | 0.0021 | 0.0011 | 0.0040 | 0.0027 | 0.0013 | 0.0056 |
| 0.981 | 0.961 | 0.993 | 0.935 | 0.873 | 0.974 | |
| λ | 0.952 | 0.898 | 0.994 | 0.952 | 0.899 | 0.994 |
| DIC | −1044.4 | −942.2 | ||||
| Likelihood-value | 902.3 | 844.7 | ||||
| Variables | PM2.5 Model | NOx Model | ||||
|---|---|---|---|---|---|---|
| Median | 2.5% | 97.5% | Median | 2.5% | 97.5% | |
| ULDI | 1.809 * | 1.341 | 2.204 | 2.120 * | 1.537 | 2.655 |
| Coastal | 0.111 | −0.070 | 0.319 | 0.033 | −0.208 | 0.262 |
| ULDI × Coastal | −1.099 * | −1.981 | −0.068 | −1.428 * | −2.491 | −0.522 |
| Other covariates | Yes | Yes | ||||
| τ2 | 0.309 | 0.269 | 0.356 | 0.355 | 0.308 | 0.410 |
| σ2 | 0.0021 | 0.0011 | 0.0042 | 0.0027 | 0.0014 | 0.0054 |
| 0.973 | 0.945 | 0.989 | 0.923 | 0.853 | 0.968 | |
| λ | 0.957 | 0.905 | 0.996 | 0.957 | 0.905 | 0.996 |
| DIC | −1035.3 | −932.1 | ||||
| Likelihood-value | 897.7 | 841.9 | ||||
| Variables | PM2.5 Model | NOx Model | ||||
|---|---|---|---|---|---|---|
| Median | 2.5% | 97.5% | Median | 2.5% | 97.5% | |
| Intercept | 10.51 * | 6.708 | 14.18 | 10.37 * | 7.308 | 14.28 |
| LD | 0.629 * | 0.411 | 0.815 | 0.791 * | 0.577 | 1.034 |
| Green | 0.010 | −0.041 | 0.061 | 0.013 | −0.037 | 0.069 |
| ACLD | 1.677 | −2.453 | 4.960 | 1.424 | −2.028 | 4.836 |
| Coastal | 0.031 | −0.205 | 0.227 | −0.020 | −0.23 | 0.177 |
| Dist_City | −0.165 * | −0.213 | −0.122 | −0.178 * | −0.224 | −0.127 |
| Dist_Xiamen | −0.417 * | −0.666 | −0.068 | −0.366 * | −0.748 | −0.123 |
| τ2 | 0.308 | 0.268 | 0.355 | 0.355 | 0.309 | 0.411 |
| σ2 | 0.0021 | 0.0011 | 0.0041 | 0.0027 | 0.0013 | 0.0055 |
| 0.979 | 0.956 | 0.992 | 0.935 | 0.874 | 0.974 | |
| λ | 0.952 | 0.899 | 0.994 | 0.950 | 0.896 | 0.993 |
| DIC | −1037.4 | −937.9 | ||||
| Likelihood-value | 898.7 | 843.4 | ||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, S.; Dong, G.; Xu, Y. A Dynamic Spatio-Temporal Analysis of Urban Expansion and Pollutant Emissions in Fujian Province. Int. J. Environ. Res. Public Health 2020, 17, 629. https://0-doi-org.brum.beds.ac.uk/10.3390/ijerph17020629
Zhao S, Dong G, Xu Y. A Dynamic Spatio-Temporal Analysis of Urban Expansion and Pollutant Emissions in Fujian Province. International Journal of Environmental Research and Public Health. 2020; 17(2):629. https://0-doi-org.brum.beds.ac.uk/10.3390/ijerph17020629
Chicago/Turabian StyleZhao, Shen, Guanpeng Dong, and Yong Xu. 2020. "A Dynamic Spatio-Temporal Analysis of Urban Expansion and Pollutant Emissions in Fujian Province" International Journal of Environmental Research and Public Health 17, no. 2: 629. https://0-doi-org.brum.beds.ac.uk/10.3390/ijerph17020629




