While the methods described in the previous section are useful for addressing many important questions, they do not rank outcomes in a way that answers our third question in a transparent manner. Fortunately, a set of tools for ranking distributions is relatively well developed in the context of income and health outcomes. The literature on applying these methods to rank environmental policy outcomes by their distributional impacts is still in its infancy, however.
In this section, we outline how this literature has been adapted to address environmental justice questions, identifying some shortcomings and suggesting some steps forward. We begin with a set of visual ranking tools, Lorenz and concentration curves, which allow one to determine easily if one distribution of outcomes is more “equitable” than another. These tools are only applicable, however, for a small set of possible distributional comparisons.
We then discuss several inequality indices, the Gini coefficient, the concentration index, the Atkinson index and the Kolm-Pollak index. Unlike the visual ranking tools, these indices permit the analyst to rank any set of distributions. This universal applicability comes at the expense of imposing additional normative assumptions, however. This tradeoff can be most easily seen with the Gini coefficient and concentration index. Although these two indices can be derived respectively from the Lorenz and concentration curves, they do not provide identical information as the curves. The indices can rank distributions that the curves cannot, but they require the analyst to impose stronger normative restrictions.
4.1. Visual Ranking Tools
We begin with two visual ranking tools, the Lorenz curve and the concentration curve. These tools have the advantage of imposing relatively few ethical standards on an ordering; however, they are unable to provide a complete ranking of distributions. In addition, they do not provide much useful information regarding distribution of environmental outcomes across subgroups, limiting their applicability to EJ analysis.
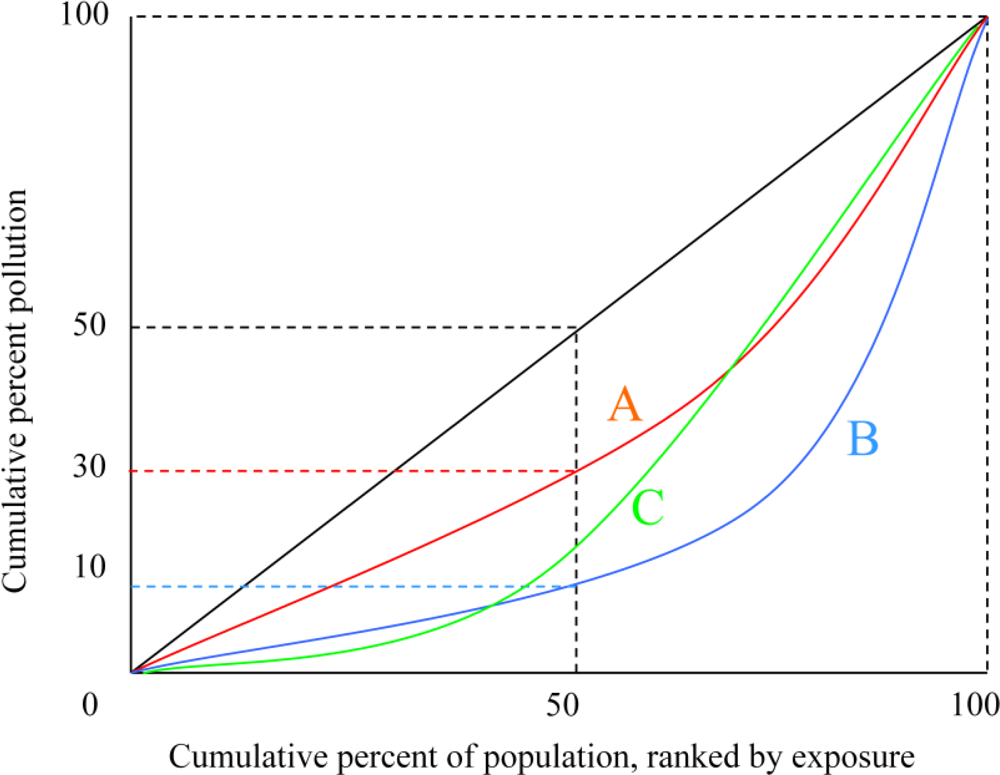
Lorenz Curves. If one accepts the ethical premise that it is always desirable to transfer a unit of pollution away from a highly exposed individual to a lesser exposed one, then Lorenz curves provide a means of ranking policy outcomes. Some hypothetical Lorenz curves for distribution of a pollutant are depicted in
Figure 1. The horizontal axis of the graph indicates percentiles of the population ranked by pollution exposure: 10 corresponds to the ten percent of the population least exposed to the pollutant, 50 corresponds to the half of the population least exposed to pollution,
etc. The vertical axis represents the percent of pollution exposed by percentile. The black diagonal line depicts a perfectly equal distribution of exposure: the lowest 10 percent of the population experience 10 percent of the exposure the lowest 50 percent of the population experience half the exposure,
etc.
Curves A, B, and C represent three hypothetical Lorenz curves in which pollution is not distributed equally. In curve A, for example, the least exposed half of the population is exposed to 30 percent of the pollution, while in curve B the least exposed half experiences only 10 percent of the pollution. Lorenz curves have the useful feature that the farther away the curve is from the diagonal, the less equal is the distribution. This property can form the basis of a ranking system. Suppose A and B represent the predicted distributions of two regulatory options. For now, let us suppose that the two policies result in the same amount of pollution per capita. Option A results in a more equitable distribution than Option B. The only value judgment that needs to be imposed to make a preference ranking is that one care at all about distributional equity. It does not matter how much one cares about exposure at the top or bottom of the distribution. As long as one prefers a more equal distribution to a less equal one, a curve that is closer to the diagonal (such as A) is preferable to a curve that is farther (such as B).
Although Lorenz curve analysis imposes minimal value judgments on the part of the analyst, it has several drawbacks that limit its practical usefulness. First, it is only a partial ordering, meaning that it can only draw meaningful comparisons for options whose Lorenz curves do not cross. A policy generating curve C, for example, cannot be compared with curves A and B since it is closer to the diagonal for some range of the population, but farther for others. This property is particularly problematic if one is interested in several options since the more curves being analyzed the more likely that some will cross.
Second, Lorenz curve analysis is ordinal; one can say that A is preferred to B, but not by how much. This ordinal property is related to a third issue. Lorenz curve analysis ignores differences in average exposure levels. For example, if we abandon the assumption that each distribution has the same average pollution level, the exposure levels of the most highly exposed individual in distribution B may be lower than the least exposed in distribution A. It may be undesirable to conclude that A is preferred to B simply because the exposure is more equitably distributed. Lorenz curves do not provide any means of evaluating a tradeoff between lower average exposure levels and a less equitable distribution. (The generalized Lorenz curve developed by Shorrocks [
29], however, does allow a partial ordering of distributions with different means.)
Finally, for purposes of environmental justice analysis, Lorenz curves have the shortcoming that they are not easily disaggregated by population subgroups. It is straightforward to use Lorenz curves to compare distributions of pollutants within a sub-group (e.g., define the population and exposure percentiles in terms of individuals below a poverty threshold). It is not so easy to use Lorenz curves to evaluate distributions across subgroups (e.g., to make statements to the effect that a regulation causes pollution to be more equitably distributed across racial groups). Although Lorenz curves can be decomposed by subgroup [
30], this decomposition does not allow one to rank distributions as in the aggregate Lorenz curve analysis.
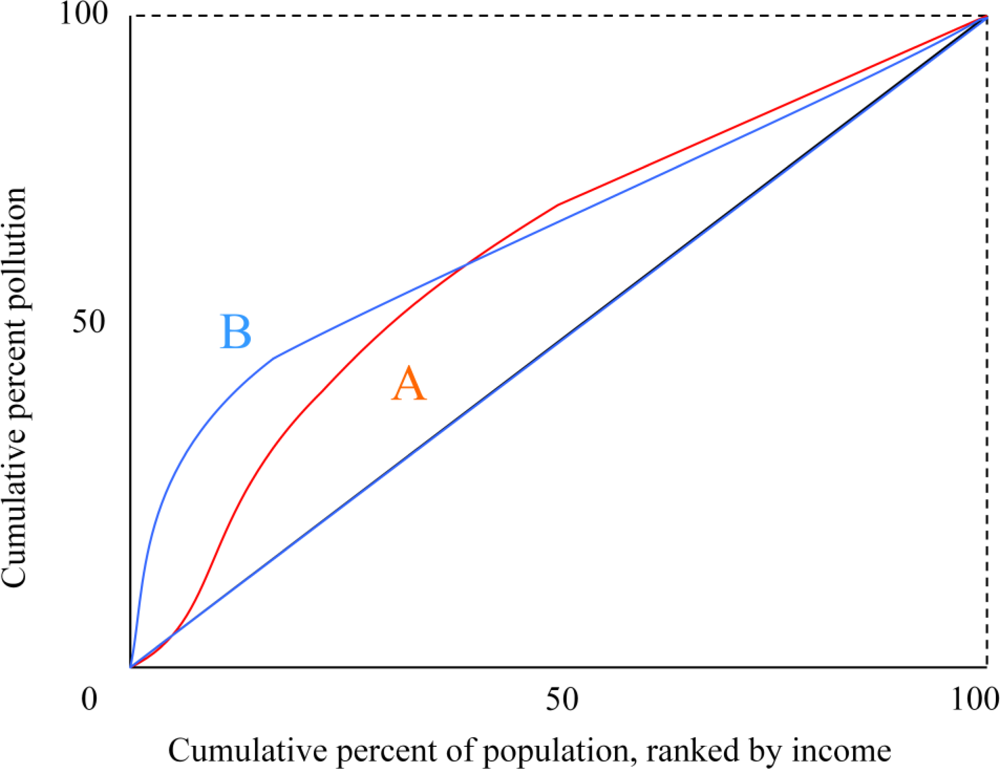
Concentration Curves. Like the Lorenz curve, the vertical axis of the concentration curve displays the share of an outcome variable experienced by a population. The horizontal axis displays the cumulative percent of the population ranked by socio-economic status (typically income). A Lorenz curve, in contrast, would display the population ranked by exposure. The height of the concentration curve indicates the share of the outcome experienced by a given cumulative proportion of the population.
Figure 2 displays hypothetical concentration curves. A perfectly equal distribution of outcomes corresponds to a concentration curve along the 45° line. Kakwani [
31] first developed this analysis to study income tax progressivity. Wagstaff
et al. [
32] proposed its use in measuring the equity of health outcomes.
Unlike Lorenz curves, concentration curves can cross the 45° line, and even lie completely above it if lower income is correlated with higher outcomes. Concentration curves can rank distributions in a manner similar to Lorenz curves; for a good outcome, a higher curve is socially more desirable. Concentration curve rankings implicitly employ social preferences such that it is always desirable to transfer a good environmental outcome away from a relatively rich individual towards a poorer one, even if the poorer individual is slightly poorer and significantly healthier [
33]. Note that this normative judgment may be more controversial than the corresponding assumption used for Lorenz curve analysis (that it is socially desirable to shift good health outcomes to the relatively ill).
Concentration curve analysis suffers from the same shortcomings as Lorenz curve analysis. It is unable to rank distributions whose curves cross, thus providing only a partial ordering. It is ordinal, and ignores differences in average exposure levels. It is also unable to evaluate changes in distributions between subgroups (other than those based on income).
In general, both visual ranking tools have some advantages over the visual displays discussed in the previous section. In some cases, both Lorenz and concentration curves allow comparisons across policy alternatives. In addition, concentration curves provide information regarding equity of an environmental outcome with respect to one demographic variable of interest, income. However, both curves share the main shortcomings of the other visual displays; they are only effective at comparing distributions if there are sufficiently stark differences. If the curves for different policy options cross, this analysis provides no effective ranking methodology.
4.2. Inequality Indices
An inequality index is a mathematical tool for converting a distribution into a single number. That number can then be used to generate an ordering for any set of outcomes, thus addressing the partial ordering issue inherent in the Lorenz and concentration curve analyses. For example, a distribution with a higher inequality index number is less equal, and hence less preferred than one with a lower number. Moreover, some inequality indices can be decomposed in a manner that allows one to evaluate inequality both within and between subgroups of interest. An index value can also have cardinal (rather than just ordinal) significance, i.e., the magnitudes, not just the rankings, contain useful information. However, these useful features come at the cost of imposing subjective value judgments. In addition, their usefulness for evaluating distributions of bads can be problematic.
Here, we focus on four families of inequality indices: the Gini coefficient, the concentration index, the Atkinson index, and the Kolm-Pollak index. For a discussion of other index numbers in the context of income distribution, see [
34]; in the context of environmental outcomes, see [
10]. These indices can be divided into the categories of relative (Gini coefficient, concentration index, and Atkinson index) and absolute (Kolm-Pollak index) indices. Relative indices are unaffected by proportionate changes in the outcome variable. They are therefore convenient for analysis of variables using different units of measurement (e.g., currencies for income analysis). In contrast, absolute indices are unaffected by a uniform shift in the outcome variable (
i.e., the addition of a constant to every individual’s outcome). These properties are mutually exclusive, and there is no unambiguous reason to choose one category of index over another. As argued by [
35], however, relative indexes can be misleading. Suppose the income of both members of a population of two individuals doubles. If prices do not change the difference in purchasing power between the two would also double, suggesting that the new distribution is less equal. An absolute inequality index would increase to reflect this change, while relative index would not.
Blackorby and Donaldson [
36,
37] show that relative and absolute indices that depend only on one variable have an associated ordinal social evaluation function (the proofs do not apply to the concentration index since it depends on two variables, environmental outcome and income). The equally distributed equivalent (EDE) value of a distribution is the amount of the outcome variable that, if given equally to every individual in the population, would leave society just as well off as the actual, unequal distribution. The EDE thus embodies a set of social preferences and is a measure of social welfare that enables rankings of distributions with different means. The Gini coefficient, Atkinson index, and Kolm-Pollak index can all be expressed as functions of their associated EDEs.
Choosing a specific type of index with which to rank policies is thus equivalent to choosing a particular social evaluation function on which to base the policy decision. Since the values of the associated social evaluation function do depend on the average value of the outcome variable (not just the distribution), they provide an additional tool with which the analyst can compare policy outcomes that differ in both mean and distribution in a logically consistent manner.
Although the social evaluation functions are ordinal, the associated inequality indices are cardinal. A relative index answers the question, “What percent of the average amount of the good would society be willing to sacrifice if the remainder were allocated evenly across the population?” An absolute index answers the question, “What is the amount of the good per capita society would be willing to sacrifice if the remainder were allocated evenly across the population?” Thus, magnitudes, not just ranking of the indexes are significant.
Gini Coefficient. The Gini coefficient is the most widely used inequality index. Its popularity is likely due more to the fact that it is easily understood as an increasing function of the area between a Lorenz curve and the diagonal line representing perfect equality than to desirable theoretical properties. The Gini coefficient has the undesirable feature that the effect of a transfer on the index number depends on the individuals’ ranks, not the difference in outcomes. In contrast to the widely accepted principle that an inequality index should place greater weight on transfers among the relatively worse off, for a typical bell-shaped distribution a transfer between individuals in the middle of the distribution will have a higher effect on the Gini coefficient than a transfer between two similarly distanced individuals at either tail [
38]. There are ways of modifying the Gini coefficient to introduce flexibility in the weights placed on different segments of the population [
39,
40]. These techniques are rarely used in practice, however.
The Gini coefficient also has the undesirable property that the effect of a transfer on the index depends on the endowment of a third individual; if that individual is ranked between the first two, the transfer will have a greater impact than if not (since there will be a greater rank difference between the first two individuals in the former case). Finally, and particularly troublesome for EJ analysis, the Gini coefficient cannot generally be used to decompose aggregate inequality into within and between group components in an internally consistent manner [
34]. Specifically, constructing an EDE for each subpopulation and then using these to construct an aggregate EDE for the entire population does not yield the same result as calculating the aggregate EDE directly.
Although it is a simple matter to compute a Gini coefficient if the outcome of concern is a bad (rather than a good), the resulting measure does not have a sensible associated social evaluation function (since it would be increasing in the bad). It is an ordinal ranking of dispersion, but loses the cardinal interpretation of a relative inequality measure since the EDE is smaller than the mean (for a bad it should be larger). Thus, it does not indicate the percent increase in average pollution that could be tolerated in exchange for a perfectly equal distribution. Consequently, the Gini coefficient can provide useful comparisons for distributions with the same mean level of a bad, but cannot be used in conjunction with a social evaluation function to rank distributions with different means. Moreover, using the Gini coefficient in this way can be misleading since it can generate different policy rankings if one uses a bad as the outcome variable versus its complementary good. Calculating the Gini coefficient for ambient concentrations of parts per billion of an air pollutant, for example, yields a different ranking of policy outcomes than using the same data to calculate a Gini coefficient for parts per billion of “clean” air.
There are several examples of applications using the Gini coefficient to analyze distributions of health and environmental outcomes. Among the first were [
41], who used a Gini coefficient to track evolution in age at death (a good) over time in Great Britain. Heil and Wodon [
42] use a Gini coefficient to examine the distribution of predicted CO
2 emissions across countries grouped by income. Millimet and Slottje [
43] use the Gini coefficient to compare distributions of pollution across states grouped by income class. Since the Gini coefficient does not satisfy consistency in aggregation both of these studies required a group overlap term in addition to between and within group terms. Millimet and Slottje [
44] use the Gini coefficient to evaluate the effect of regulatory compliance costs on the distribution of toxics reported in the U.S. Toxic Release Inventory across U.S. states and counties. They combine regression results with Spearman correlations between demographic characteristics and emissions to argue that policies that increase inequality as measured by the Gini coefficient increase racial disparities. In these studies, the Gini coefficient has been used primarily as an ordinal measure of dispersion, without attendant welfare implications.
Concentration Index. The concentration index is similar to the Gini coefficient, being an increasing function of the difference between the 45° line and the concentration (rather than Lorenz) curve. For details on the practical use of the concentration index, see [
15]. Its value ranges from −1 (the entire outcome is borne by the poorest individual) to 1 (the entire outcome is borne by the wealthiest individual). Since the concentration curve can cross the 45° line, zero either indicates perfect equality or that the area above the curve is exactly equal to the area below it. As with the Gini coefficient, the effect of allocating a unit of the outcome variable to an individual is weighted by the individual’s rank. With the concentration index, the relevant rank is income, rather than the outcome variable.
The concentration index can provide a complete ordering in the sense that lower values are always more “pro-poor” (for distribution of a good) than higher values. The cardinal relationship between magnitudes of concentration index numbers lacks the clear intuition of the other three indices considered here, however. This is not to say that there is no intuitive interpretation. Koolman and van Doorslaer [
45] provide a link between the index value and the proportionate amount of the outcome variable that would need to be redistributed from the richest to the poorest half of the population in order to attain an index value of zero (not necessarily equality).
Like the Gini coefficient, the concentration index value depends on individuals’ ranks, not absolute differences. It also shares the trait that ordering based on the concentration index can be sensitive to whether the outcome variable is expressed as a good or its “bad” complement [
46]. It inherits from the concentration curves the questionable normative assumption that transfers of a good environmental outcome from rich to poor is always desirable [
47].
Atkinson Index. The Atkinson index satisfies several desirable theoretical properties lacking in other relative indices [
35,
36,
38]. Among these are that it is a function of individual allocations rather than rank, and it can be disaggregated into subgroups in a consistent manner (see also [
48]).
In its formula, the Atkinson index explicitly incorporates ethical considerations with an inequality aversion parameter that ranges from zero to infinity. This parameter introduces some flexibility, allowing the analyst to specify the amount society is willing to trade a reduction in the outcome variable for one individual for an increase for another. A value of zero implies that society is indifferent between transfers between any two individuals. The higher the parameter’s value, the more weight society places on transfers to individuals with lower outcomes. Since the choice of a parameter value is entirely normative, it is common to calculate Atkinson indexes for several values to determine how sensitive rankings are to the choice.
Although the Atkinson index has many desirable properties when used to analyze distributions of goods, it is not so convenient for analyzing bad outcomes. As with the Gini coefficient, inputting a bad into the Atkinson formula removes any cardinal welfare significance since the associated social evaluation function would be increasing in the bad. It also causes the index to place more weight upon the most well-off individuals (those with low outcomes), rather than the worst off. The Atkinson index is generally not defined for negative numbers, thus precluding a simple redefinition of bads in that way. Even for examples in which negative values are defined, the Atkinson Index generates the perverse result that a progressive redistribution reduces social welfare [
49].
Transforming a bad into a good by replacing it with its complement (e.g., parts per billion of a pollutant to parts per billion of “clean” air, or the probability of not dying from cancer) may have the undesirable result of rendering an index value so small as to be within rounding error. To put this in perspective, consider the relative income distribution of a society of billionaires who differed in wealth by only a few dollars. It would be almost perfectly equal, with the value of the corresponding Atkinson index being extremely close to zero. Note that this does not mean that the distributional effects are insignificant. If the good were clean air or probability of not dying from cancer the percent reduction society would be willing to give up for an equal distribution might be quite small, but the value of that reduction might be significant. Nonetheless, presenting the results in a manner such that a regulation changes the Atkinson Index by a miniscule amount may not be easy to interpret.
Although the Atkinson index is commonly used in income distribution analysis, it has rarely been used to measure environmental or health outcomes. Waters [
50] used an Atkinson index to analyze distribution of access to health care (a good) in Ecuador. Levy
et al. [
20] used the Atkinson index to evaluate the distribution of mortality risk resulting from alternative power plant air pollution control strategies in the United States. Levy
et al. [
51] used the Atkinson index to analyze reduction in mortality risk from particulate matter reductions from regulating transportation. Each of these studies used the Atkinson index as a measure of dispersion without welfare significance.
Kolm-Pollak Index. The Kolm-Pollak index shares the desirable theoretical properties of the Atkinson index [
35,
37,
48]. It also uses an inequality aversion parameter to specify the relative importance of allocations to different segments of the population. Higher values correspond to greater weight being placed on the worse off and zero indicates complete indifference to the allocation.
In contrast with the other indices examined here, the Kolm-Pollak index readily accommodates bad outcomes. It is inappropriate to input bad values directly into the index. However, one can simply multiply them by minus one and add them to some arbitrary benchmark. This operation preserves the appropriate social evaluation function ranking and is equivalent to measuring the distribution of a complementary “good.” The property of an absolute index that adding the same amount to everyone in the population does not change its value helps in this regard; the value of the index is independent of the benchmark level. To date, the Kolm-Pollak index has not been used in the analysis of environment or health outcomes, and there are few examples of its application in income analysis (an exception is [
52]).
In general, the Atkinson and Kolm-Pollak inequality indices have the potential to inform all three questions posed in Section 2. They can provide a concise snapshot the dispersion of environmental outcomes for baseline and policy scenarios, both within and across population subgroups. In terms of ranking outcomes, they can be used to determine whether policy alternatives improve the dispersion of outcomes, holding the total amount of the outcome constant. For good outcomes the social evaluation functions associated with both indices can also be used to rank alternatives for which both the dispersion and total amount of pollution vary. Only the Kolm-Pollak index appears suitable for evaluation of bad outcomes, however.