Investigating the Causal Linkages among Inflation, Interest Rate, and Economic Growth in Pakistan under the Influence of COVID-19 Pandemic: A Wavelet Transformation Approach
Abstract
:1. Introduction
Theoretical Background
2. Literature Review
3. Research Methodology
3.1. What Is Wavelet Transformation?
3.2. Wavelet Power Spectrum
3.3. The Cross-Wavelet Power Spectrum
3.4. Wavelet Coherence (WTC)
4. Data Description and Stylized Facts
5. Wavelet Estimations and Discussion
5.1. Continuous Wavelet Power Spectrum (CWT)
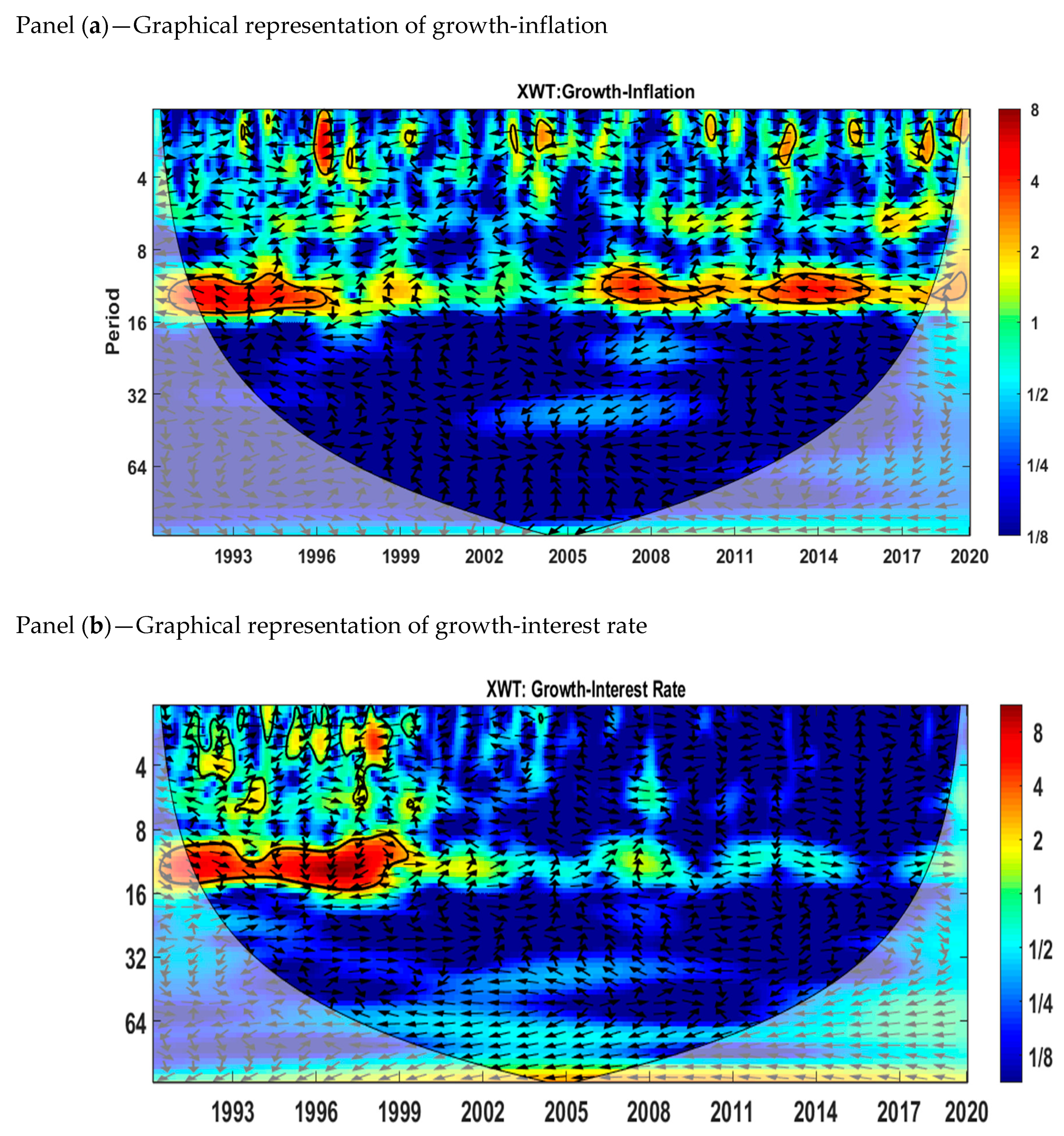
5.2. Cross-Wavelet Transform (XWT)
5.3. Cross-Wavelet Coherence (WTC)
5.4. Multi-Scale Granger Causality Tests
6. Conclusions and Policy Implications
Limitation and Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Aguiar-Conraria, Luís, and Maria Joana Soares. 2011. Oil and the Macroeconomy: Using Wavelets to Analyze Old Issues. Empirical Economics 40: 645–55. [Google Scholar] [CrossRef]
- Aguiar-Conraria, Luís, Nuno Azevedo, and Maria Joana Soares. 2008. Using Wavelets to Decompose the Time-Frequency Effects of Monetary Policy. Physica A: Statistical Mechanics and Its Applications 387: 2863–78. [Google Scholar] [CrossRef] [Green Version]
- Aloui, Chaker, and Besma Hkiri. 2014. Co-Movements of GCC Emerging Stock Markets: New Evidence from Wavelet Coherence Analysis. Economic Modelling 36: 421–31. [Google Scholar] [CrossRef]
- Andrés, Javier, and Ignacio Hernando. 1997. Does Inflation Harm Economic Growth? Evidence for the OECD. Working Paper 6062. Cambridge: National Bureau of Economic Research. [Google Scholar]
- Anidiobu, Gabriel, Paschal I. P. Okolie, and D. C. Oleka. 2018. Analysis of Inflation and Its Effect on Economic Growth in Nigeria. IOSR Journal of Economics and Finance 9: 28–36. [Google Scholar] [CrossRef]
- Asghar, Nabila, Maryam Batool, Fatima Farooq, and Hafeez ur Rehman. 2020. Covid-19 Pandemic and Pakistan Economy: A Preliminary Survey. Review of Economics and Development Studies 6: 447–59. [Google Scholar] [CrossRef]
- Aßhoff, Sina, Belke Ansgar, and Osowski Thomas. 2020. Unconventional Monetary Policy and Inflation Expectations in the Euro Area, Ruhr Economic Papers 837, RWI-Leibniz-Institutfür Wirtschaftsforschung, Ruhr-University Bochum, TU Dortmund University, University of Duisburg-Essen. Available online: https://ideas.repec.org/p/zbw/rwirep/837.html (accessed on 15 April 2021).
- Ayyoub, Muhammad, Imran Sharif Chaudhry, and Fatima Farooq. 2011. Does Inflation Affect Economic Growth? The case of Pakistan. Pakistan Journal of Social Sciences (PJSS) 31. [Google Scholar]
- Barro, Robert J. 1995. Inflation and Economic Growth. NBER Working Paper. Cambridge: National Bureau of Economic Research, p. 5326. [Google Scholar]
- Batool, Maryam, Huma Ghulam, Muhammad Azmat Hayat, Muhammad Zahid Naeem, Abdullah Ejaz, Zulfiqar Ali Imran, Cristi Spulbar, Ramona Birau, and Tiberiu Horațiu Gorun. 2020. How COVID-19 Has Shaken the Sharing Economy? An Analysis Using Google Trends Data. Economic Research-Ekonomska Istrazivanja, 1–13. [Google Scholar] [CrossRef]
- Benhmad, François. 2013. Dynamic Cyclical Comovements between Oil Prices and US GDP: A Wavelet Perspective. Energy Policy 57: 141–51. [Google Scholar] [CrossRef]
- Bhaduri, Saumitra. 2016. Revisiting the Growth-Inflation Nexus: A Wavelet Analysis. Economic Notes 45: 79–89. [Google Scholar] [CrossRef] [Green Version]
- Bhattacharya, Prabir C. 1995. The economics of development: A review article. Journal of Economic Studies 22: 59–74. [Google Scholar] [CrossRef]
- Bibow, Jörg. 2002. What Has Happened to Monetarism? An Investigation into the Keynesian roots of Milton Friedman’s Monetary Thought and its Apparent Monetarist Legacies. Working Paper, No. 347. Annandale-on Hudson: Levy Economics Institute of Bard College. [Google Scholar]
- Bittencourt, Manoel, Reneé Van Eyden, and Monaheng Seleteng. 2015. Inflation and Economic Growth: Evidence from the Southern African Development Community. South African Journal of Economics 83: 411–24. [Google Scholar] [CrossRef] [Green Version]
- Briotti, Gabriella. 2005. Economic reactions to public finance consolidation: A survey of the literature. ECB Occasional Paper 38. [Google Scholar]
- Bruno, Michael, and William Easterly. 1998. Inflation Crises and Long-Run Growth. Journal of Monetary Economics 41: 3–26. [Google Scholar] [CrossRef] [Green Version]
- Cai, Xiaojing, Zheng Fang, Youngho Chang, Shuairu Tian, and Shigeyuki Hamori. 2020. Co-Movements in Commodity Markets and Implications in Diversification Benefits. Empirical Economics 58: 393–425. [Google Scholar] [CrossRef]
- Chimobi, Omoke Philip. 2010. Inflation and economic growth in Nigeria. Journal of Sustainable Development 3: 159. [Google Scholar]
- Chowdhury, Anis. 2002. Does Inflation Affect Economic Growth? The Relevance of the Debate for Indonesia. Journal of the Asia Pacific Economy 7: 20–34. [Google Scholar] [CrossRef]
- Clague, Christopher K. 1997. Institutions and Economic Development, Growth and Governance in Less-Developed and Post-Socialist Countries. Baltimore: The Johns Hopkins University Press. [Google Scholar]
- Coibion, Olivier, Yuriy Gorodnichenko, and Tiziano Ropele. 2018. Inflation Expectations and Firm Decisions: New Causal Evidence. Working Paper 25412. Cambridge: National Bureau of Economic Research, Available online: http://www.nber.org/papers/w25412 (accessed on 15 April 2021).
- Crowley, Patrick M. M. 2011. An Intuitive Guide to Wavelets for Economists. SSRN Electronic Journal, 1–68. [Google Scholar] [CrossRef] [Green Version]
- Dar, Arif Billah, Niyati Bhanja, and Aviral Kumar Tiwari. 2014. Inflation-Industrial Growth Nexus in India—A Revisit through Continuous Wavelet Transform. Central Bank Review 14: 1–11. [Google Scholar]
- Datta, Kanchan, and Chandan Kumar Mukhopadhyay. 2011. Relationship between Inflation and Economic Growth in Malaysia. An Econometric Review 4: 415–19. [Google Scholar]
- Daubechies, Ingrid. 1992. Ten Lectures on Wavelets. Computers in Physics 6, no. 6: 697. Pennsylvania: Society for Industrial and Applied Mathematics. [Google Scholar] [CrossRef] [Green Version]
- Davcev, Ljupco, Nikolas Hourvouliades, and Jasmin Komic. 2018. Impact of interest rate and inflation on GDP in Bulgaria, Romania and FYROM. Journal of Balkan and Near Eastern Studies 20: 131–47. [Google Scholar] [CrossRef] [Green Version]
- De Gregorio, Jose. 1991. The Effects of Inflationon Economic Growth: Lessons from Latin America. IMF Working Papers 91: 1. [Google Scholar] [CrossRef]
- Deardorff, Alan V. 2001. Developing country growth and developed country response. The Journal of International Trade and Economic Development 10: 373–92. [Google Scholar] [CrossRef]
- Di Giovanni, Julian, Justin McCrary, and Till von Wachter. 2009. Following Germany’s Lead: Using International Monetary Linkages to Estimate the Effect of Monetary Policy on the Economy. Review of Economics and Statistics 91: 315–31. [Google Scholar] [CrossRef] [Green Version]
- Dickey, David A., and Wayne A. Fuller. 1979. Distribution of the estimators for autoregressive time series with a unit root. Journal of the American Statistical Association 74: 427–31. [Google Scholar]
- Dinh, Doan Van. 2020. Impulse Response of Inflation to Economic Growth Dynamics: VAR Model Analysis. Journal of Asian Finance, Economics and Business 7: 219–28. [Google Scholar] [CrossRef]
- Dornbusch, Rudi, Carlo Favero, and Francesco Giavazzi. 1998. Immediate challenges for the European central bank. Economic Policy 13: 16–64. [Google Scholar] [CrossRef] [Green Version]
- Essaied, Hamrita Mohamed. 2013. Export-Led Growth in Tunisia: A Wavelet Filtering Based Analysis. Business and Economic Horizons 9: 12–27. [Google Scholar] [CrossRef] [Green Version]
- Feldman, Maryann, Theodora Hadjimichael, Lauren Lanahan, and Tom Kemeny. 2016. The logic of economic development: A definition and model for investment. Environment and Planning C: Government and Policy 34: 5–21. [Google Scholar] [CrossRef]
- Friedman, Milton. 1961. The lag in effect of monetary policy. Journal of Political Economy 69: 447–66. [Google Scholar] [CrossRef]
- Gallegati, Marco, Mauro Gallegati, James Bernard Ramsey, and Willi Semmler. 2011. The US Wage Phillips Curve across Frequencies and over Time. Oxford Bulletin of Economics and Statistics 73: 489–508. [Google Scholar] [CrossRef]
- Garside, W. R. 2007. Introduction: Economic Growth and Development—An Institutional Perspective. In Institutions and Market Economies. London: Algrave Macmillan. [Google Scholar] [CrossRef]
- Gençay, Ramazan, Faruk Selçuk, and Brandon Whitcher. 2001. Scaling Properties of Foreign Exchange Volatility. Physica A: Statistical Mechanics and Its Applications 289: 249–66. [Google Scholar] [CrossRef]
- Gençay, Ramazan, Faruk Selçuk, and Brandon Whitcher. 2003. Systematic Risk and Timescales. Quantitative Finance 3: 108–16. [Google Scholar] [CrossRef]
- Grubaugh, Stephen G. 2015. Economic growth and growth in human development, Applied Econometrics and International Development. Euro-American Association of Economic Development 15: 5–16. [Google Scholar]
- Gülşen, Eda, and Erdal Özmen. 2020. Monetary policy trilemma, inflation targeting and global financial crisis. International Journal of Finance and Economics 25: 286–96. [Google Scholar] [CrossRef]
- Harswari, Muhammad Hariz, Afiq Bin Nor, and Sahibzada Muhammad Hamza. 2017. The impact of interest rate on economic development: A study on Asian countries. International Journal of Accounting and Business Management 5: 180–88. [Google Scholar]
- Hossain, Md Elias, Bikash Chandra Ghosh, and Md Khairul Islam. 2012. Inflation and economic growth in Bangladesh. Researchers World 3: 85. [Google Scholar]
- Hussain, Shahzad, and Shahnawaz Malik. 2011. Inflation and Economic Growth: Evidence from Pakistan. International Journal of Economics and Finance 3: 262–76. [Google Scholar] [CrossRef]
- Hwang, Jen-Te, and Ming-Jia Wu. 2011. Inflation and economic growth in China: An empirical analysis. China and World Economy 19: 67–84. [Google Scholar] [CrossRef]
- International Monetary Fund. 2021. World Economic Outlook, Managing Divergent Recoveries, World Economic Studies, Division Research Department. p. 192. Available online: https://www.imf.org/en/Publications/WEO/Issues/2021/03/23/world-economic-outlook-april-2021 (accessed on 15 April 2021).
- Jawaid, Syed Tehseen, Imrana Saif, and Amana Maroof. 2019. International Tourism and Consumer Prices in Pakistan: A Wavelet-Based Analysis. Asia Pacific Journal of Tourism Research 24: 763–77. [Google Scholar] [CrossRef]
- Kasidi, Faraji, and Kenani Mwakanemela. 2013. Impact of inflation on economic growth: A case study of Tanzania. Asian Journal of Empirical Research 3: 363–80. [Google Scholar]
- Kumar, Vijay, Acharya Sanjeev Ho, and Ly T. H. 2020. Does Monetary Policy Influence the Profitability of Banks in New Zealand? International Journal of Financial Studies 8: 35. [Google Scholar] [CrossRef]
- Madurapperuma, Wasanthi. 2016. Impact of inflation on economic growth in Sri Lanka. Journal of World Economic Research 5: 1–7. [Google Scholar] [CrossRef] [Green Version]
- Maliszewska, Maryla, Aaditya Mattoo, and Dominique van der Mensbrugghe. 2020. The Potential Impact of COVID-19 on GDP and Trade: A Preliminary Assessment. East Asia and the Pacific Region Office of the Chief Economist & Macroeconomics, Trade and Investment Global Practice. World Bank, Policy Research Working Paper. Available online: https://openknowledge.worldbank.org/bitstream/handle/10986/33605/The-Potential-Impact-of-COVID-19-on-GDP-and-Trade-A-Preliminary-Assessment.pdf (accessed on 15 April 2021).
- Mallik, Girijasankar, and Anis Chowdhury. 2001. Inflation and Economic Growth: Evidence from Four South Asian Countries. Asia-Pacific Development Journal 8: 123–35. [Google Scholar]
- Mensah, Alice Constance, and Ebenezer Okyere. 2015. Real economic growth rate in Ghana: The impact of interest rate, inflation rate and GDP. Global Journal of Research in Business and Management 4: 206–12. [Google Scholar]
- Meyer, Yves. 1986. Wavelets and spline functions. Seminar Partial Differential Equations (Polytechnique) 6: 1–18. [Google Scholar]
- Mou, Jinjin. 2020. Research on the Impact of COVID19 on Global Economy. AEECE 2020 IOP Conf. Series: Earth and Environmental Science 546: 032043. [Google Scholar] [CrossRef]
- Naeem, Muhammad Zahid, Sumera Arshad, Ramona Birau, Cristi Spulbar, Abdullah Ejaz, Muhammad Azmat Hayat, and Jenica Popescu. 2021. Investigating the impact of CO2 emission and economic factors on infants health: A case study for Pakistan. Industria Textila 72: 39–49. [Google Scholar] [CrossRef]
- Nguyen, Tung, and Tian-Xiao He. 2015. Wavelet Analysis and Applications in Economics and Finance. Journal of Statistics and Mathematical Science 1: 22–37. [Google Scholar]
- Nikkinen, Jussi, Seppo Pynnönen, Mikko Ranta, and Sami Vähämaa. 2011. Cross-Dynamics of Exchange Rate Expectations: A Wavelet Analysis. International Journal of Finance and Economics 16: 205–17. [Google Scholar] [CrossRef]
- Paul, Satya, Colm Kearney, and Kabir Chowdhury. 1997. Inflation and economic growth: A multi-country empirical analysis. Applied Economics 29: 1387–401. [Google Scholar] [CrossRef]
- Percival, Donald B., and Andrew T. Walden. 2000. Wavelet Methods for Time Series Analysis. London: Cambridge University Press, ISBN 9780511841040. [Google Scholar] [CrossRef]
- Perron, Pierre, and Serena Ng. 1996. Useful modifications to some unit root tests with dependent errors and their local asymptotic properties. The Review of Economic Studies 63: 435–63. [Google Scholar] [CrossRef] [Green Version]
- Pesaran, M. Hashem, Yongcheol Shin, and Richard J. Smith. 2001. Bounds testing approaches to the analysis of level relationships. Journal of Applied Econometrics 16: 289–326. [Google Scholar] [CrossRef]
- Ramlan, Hamidah, Mohd Shafiq, and Izani Bin Suhaimi. 2017. The Relationship Between Interest Rates and Inflation Toward the Economic Growth in Malaysia. Journal of Humanities, Language, Culture and Business (HLCB) 1: 1268147. [Google Scholar]
- Ramsey, James. B. 2002. Studies in Nonlinear Dynamics and Econometrics Wavelets in Economics and Finance: Past and Future Wavelets in Economics and Finance. Past and Future 6: 1–27. [Google Scholar]
- Raza, Syed Ali, Muhammad Shahbaz, Rafi Amir-ud-Din, Rashid Sbia, and Nida Shah. 2018. Testing for wavelet based time-frequency relationship between oil prices and US economic activity. Energy 154: 571–80. [Google Scholar] [CrossRef]
- Rua, António, and Luís C. Nunes. 2009. International Comovement of Stock Market Returns: A Wavelet Analysis. Journal of Empirical Finance 16: 632–39. [Google Scholar] [CrossRef] [Green Version]
- Rua, António. 2012. Wavelets in Economics. Economic Bulletin and Financial Stability Report Articles and Banco de Portugal Economic Studies, Banco de Portugal, Economics and Research Department. pp. 71–79. Available online: https://www.bportugal.pt/sites/default/files/anexos/papers/ab201208_e.pdf (accessed on 15 April 2021).
- Saaed, Afaf. A. 2007. Inflation and economic growth in Kuwait: 1985–2005-Evidence from co-integration and error correction model. Applied Econometrics and International Development 7: 143–55. [Google Scholar]
- Schleicher, Christoph. 2002. An Introduction to Wavelets for Economists (No. 2002-3). Ottawa: Monetary and Financial Analysis Department, Bank of Canada. [Google Scholar]
- Shahbaz, Muhammad, Tiwari Aviral Kumar, and Tahir Mohammad Iqbal. 2013. Analyzing Time-Frequency Relationship between Oil Price and Exchange Rate in Pakistan through Wavelets, COMSATS Institute of Information Technology, Lahore, Pakistan, Paper No. 48086. Available online: https://mpra.ub.uni-muenchen.de/48086/MPRA (accessed on 15 April 2021).
- Shahid, Muhammad. 2014. Effect of Inflation and Unemployment on Economic Growth in Pakistan. Journal of Economics and Sustainable Development 5: 103–7. [Google Scholar]
- Singh, R. C. 2013. Wavelet transforms in time series analysis. İstanbul Aydın Üniversitesi Dergisi 3: 61–94. [Google Scholar]
- Smyth, David. J. 1994. Inflation and growth. Journal of Macroeconomics 16: 261–70. [Google Scholar] [CrossRef]
- Sumon, Khairul Kabir, and Sazib Miyan. 2017. Inflation and Economic Growth: An Empirical Evidence of Bangladesh 1986–2016. International Journal of Economics and Financial Issues 7: 454–64. [Google Scholar]
- Swastika, Purti, Ginanjar Dewandaru, and Mansur Masih. 2013. The Impact of Debt on Economic Growth: A Case Study of Indonesia. MPRA Paper 58837. Munich: University Library of Munich. [Google Scholar]
- Taderera, Christie, Runganga Raynold, Mhaka Simbarashe, and Mishi Syden. 2021. Inflation, Interest Rate and Economic Growth Nexuses in SACU Countries, MPRA Paper No. 105419. Available online: https://mpra.ub.uni-muenchen.de/105419/ (accessed on 27 May 2021).
- Tiwari, Aviral Kumar, Arif Billah Dar, and Niyati Bhanja. 2013. Oil Price and Exchange Rates: A Wavelet Based Analysis for India. Economic Modelling 31: 414–22. [Google Scholar] [CrossRef]
- Toda, Hiro Y., and Taku Yamamoto. 1995. Statistical inference in vector autoregressions with possibly integrated processes. Journal of Econometrics 66: 225–50. [Google Scholar] [CrossRef]
- Torrence, Christopher, and Gilbert P. Compo. 1998. A practical guide to wavelet analysis. Bulletin of the American Meteorological Society 79: 61–78. [Google Scholar] [CrossRef] [Green Version]
- Uddin, Gazi Salah, Ahmed Taneem Muzaffar, Mohamed Arouri, and Bo Sjö. 2017. Understanding the Relationship between Inflation and Growth: A Wavelet Transformation Approach in the Case of Bangladesh. World Economy 40: 1918–33. [Google Scholar] [CrossRef]
- Vacha, Lukas, and Jozef Barunik. 2012. Co-Movement of Energy Commodities Revisited: Evidence from Wavelet Coherence Analysis. Energy Economics 34: 241–47. [Google Scholar] [CrossRef] [Green Version]
- Varona, Luis, and Jorge R. Gonzales. 2021. Dynamics of the impact of COVID-19 on the economic activity of Peru. PLoS ONE 16: e0244920. [Google Scholar] [CrossRef]
- Vitenu-Sackey, Prince Asare, and Richard Barfi. 2021. The Impact of Covid-19 Pandemic on the Global Economy: Emphasis on Poverty Alleviation and Economic Growth, The Economics and Finance Letters. Conscientia Beam 8: 32–43. [Google Scholar]
- WHO. 2020. Statement on the Second Meeting of the International Health Regulations (2005) Emergency Committee Regarding the Outbreak of Novel Coronavirus (2019-nCoV). Geneva: World Health Organization, Available online: https://www.who.int/news-room/detail/30-01-2020-statement-on-the-second-meeting-of-the-international-health-regulations-(2005)emergencycommittee-regarding-the-outbreak-of-novel-coronavirus-(2019-ncov) (accessed on 20 May 2021).
- World Bank. 2021. World Bank Country and Lending Groups, Country Classification. Available online: https://datahelpdesk.worldbank.org/knowledgebase/articles/906519-world-bank-country-and-lending-groups (accessed on 20 May 2021).
- Yang, Lu, Shuairu Tian, Wei Yang, Mingli Xu, and Shigeyuki Hamori. 2018. Dependence Structures between Chinese Stock Markets and the International Financial Market: Evidence from a Wavelet-Based Quantile Regression Approach. North American Journal of Economics and Finance 45: 116–37. [Google Scholar] [CrossRef]
- Yang, Lu, Xiao Jing Cai, and Shigeyuki Hamori. 2017. Does the Crude Oil Price Influence the Exchange Rates of Oil-Importing and Oil-Exporting Countries Differently? A Wavelet Coherence Analysis. International Review of Economics and Finance 49: 536–47. [Google Scholar] [CrossRef]
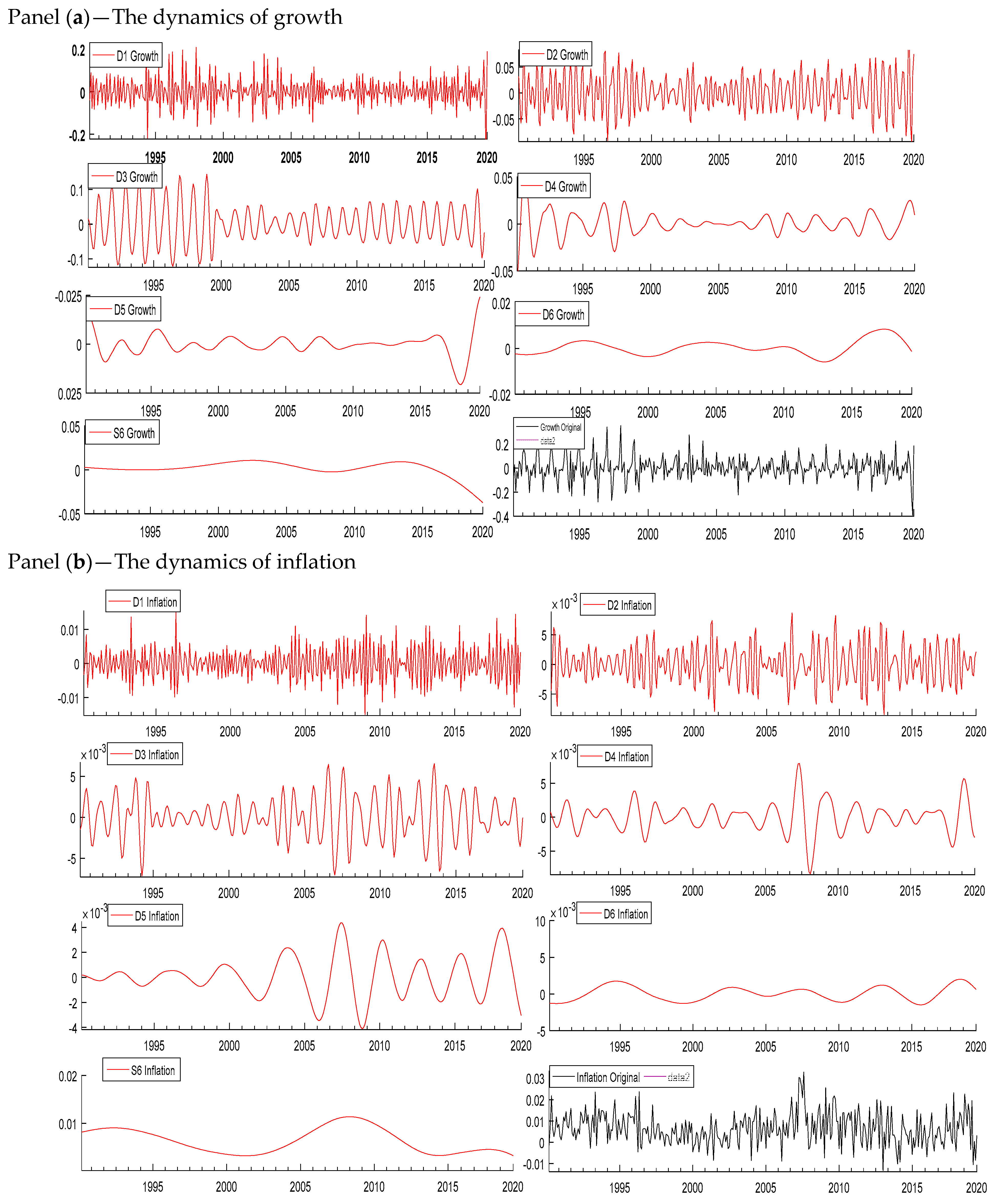
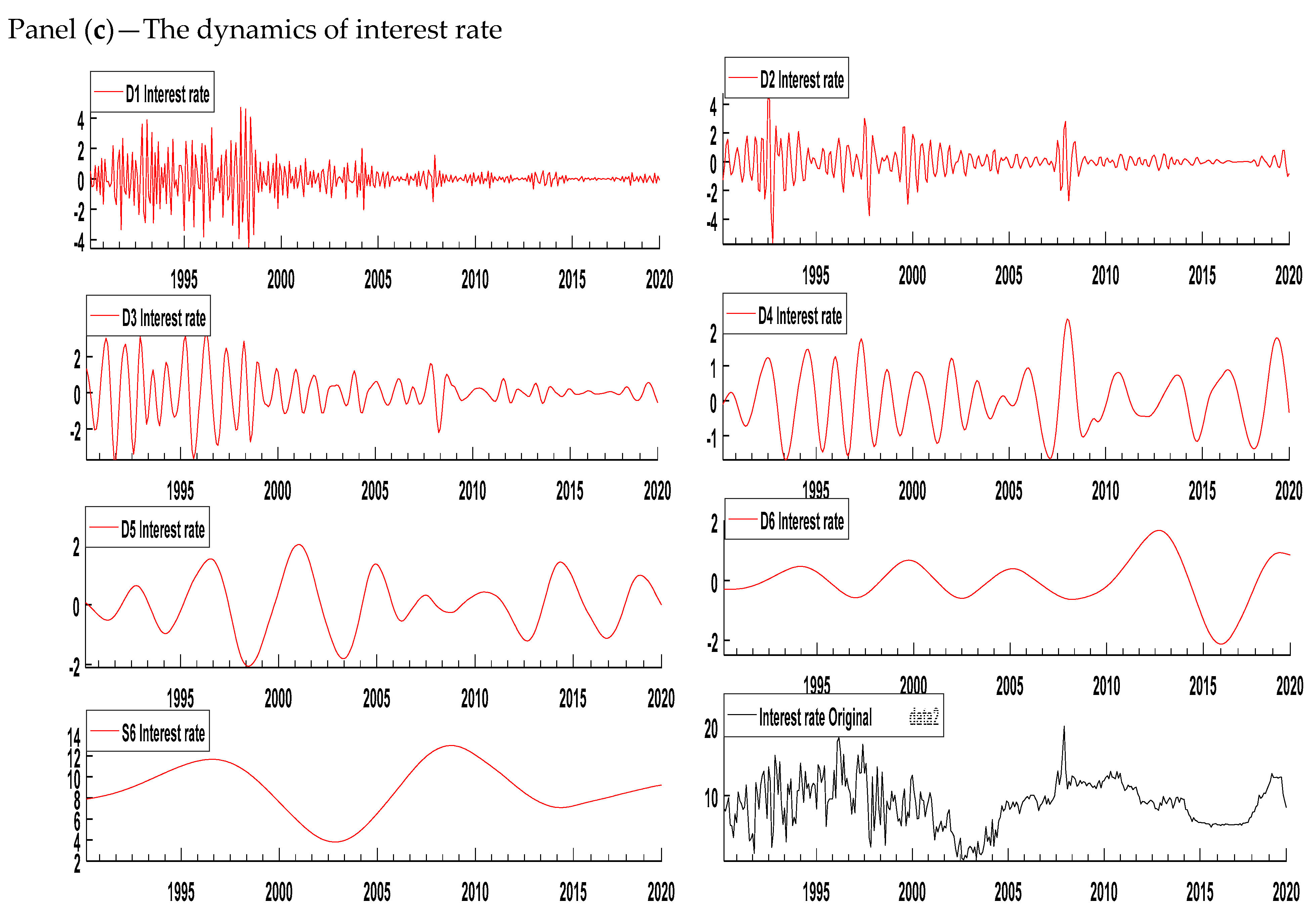
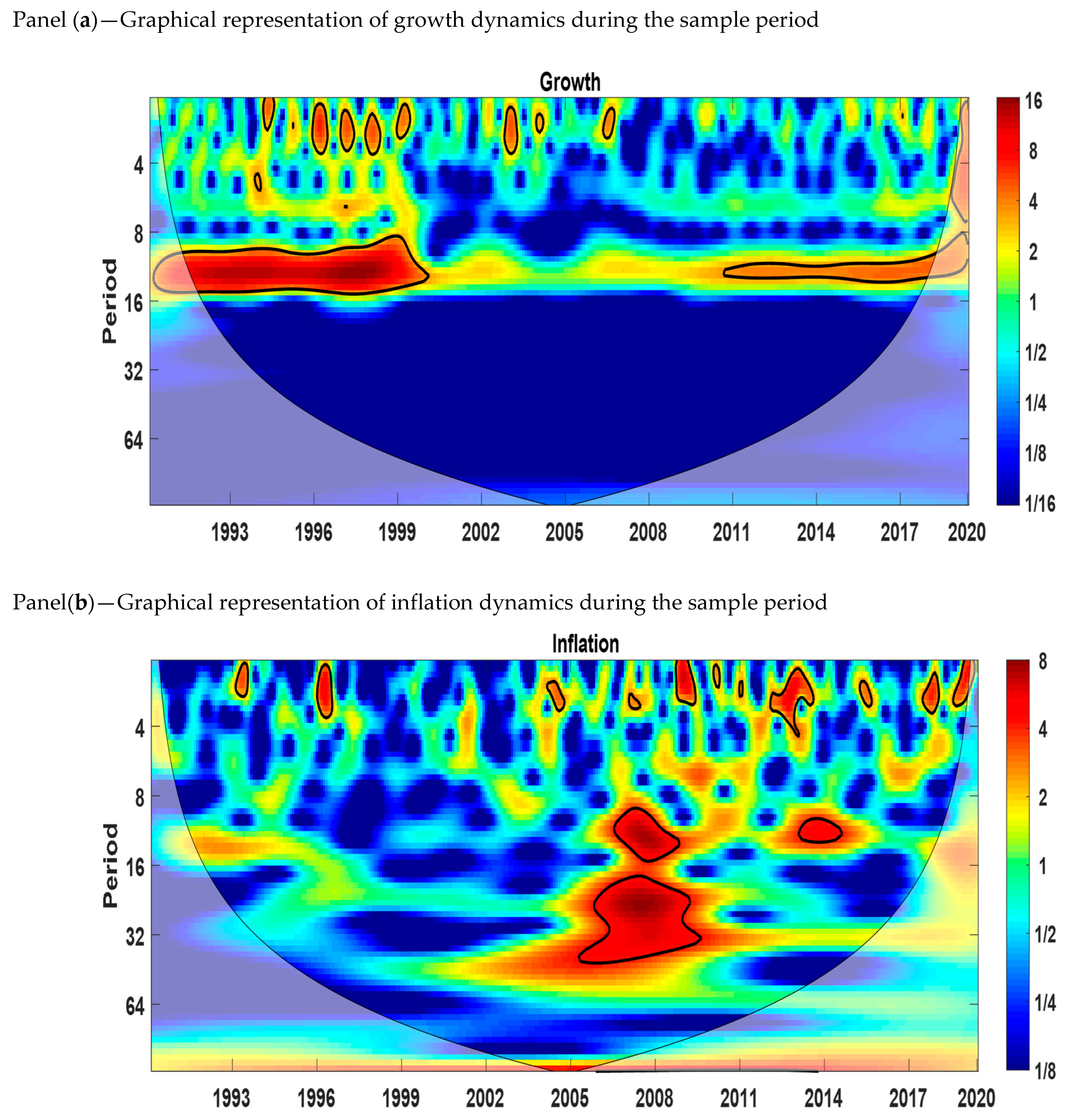
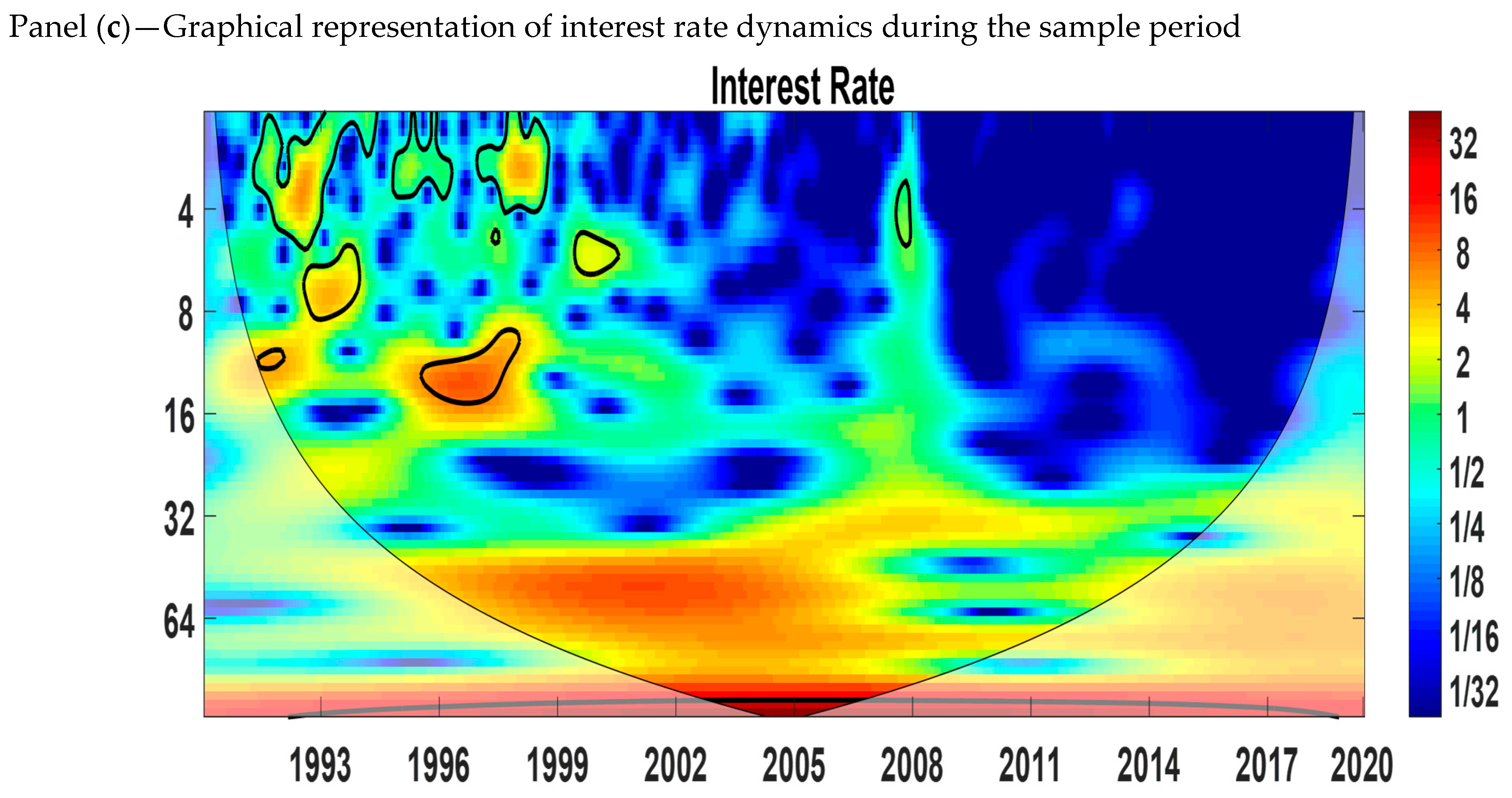

| Variables | Mean | Standard Deviation | Skewness | Kurtosis | Observations |
|---|---|---|---|---|---|
| Interest Rate change (MOM) | 0.0004 | 2.4856 | 0.4904 | 7.2421 | 352 |
| Growth | 0.0019 | 0.0936 | 0.0143 | 5.0388 | 352 |
| Inflation | 0.0065 | 0.0074 | 0.4097 | 3.4237 | 352 |
| Variables | Dickey–Fuller | Phillips–Perron |
|---|---|---|
| LN(IPI) | −2.181 (0.213) | −2.161 (0.220) |
| LN(CPI) | −1.352 (0.605) | −1.087 (0.720) |
| Growth | −17.523 *** (0.000) | −17.480 *** (0.000) |
| Inflation | −15.614 *** (0.000) | −16.068 *** (0.000) |
| Interest Rate | −7.319 *** (0.000) | −7.004 *** (0.000) |
| Bound Test F-Value | Lower Bound | Upper Bound |
|---|---|---|
| (at 5%) | ||
| 12.36 *** | 3.1 | 3.87 |
| Long-Run Coefficients | ||
| Dependent Variable: Economic Growth | Coefficient | SE |
| Inflation | 0.58 *** | 0.03 |
| Interest rate | −0.03 *** | 0.01 |
| Constant | 2.22 *** | 0.19 |
| Adj. R-square | 0.96 | |
| Causality Tests | Causality Path | F-Statistic |
|---|---|---|
| Pairwise Granger Causality | GDP→INF | 36.901 *** |
| INF→GDP | 135.65 *** | |
| GDP→IR | 3.024 * | |
| IR→GDP | 28.983 *** | |
| Toda–Yamamoto Causality | GDP→INF | 47.234 *** |
| INF→GDP | 164.400 *** | |
| GDP→IR | 5.904 ** | |
| IR→GDP | 33.948 *** |
| Wavelet Scales | Time Horizon | Economic Horizon |
|---|---|---|
| D1 | 2 to 4 months | Short run |
| D2 | 4 to 8 months | |
| D3 | 8 to 16 months | Medium run |
| D4 | 16 to 32 months | |
| D5 | 32 to 64 months | Long run |
| D6 | 64 to 128 months | |
| S6 | Above 128 months | Very long run |
| Null Hypothesis | Test Value | p-Value |
|---|---|---|
| D1 Growth ≠> D1 Inflation | 5.818 | 0.009 |
| D2 Growth ≠> D2 Inflation | 0.585 | 0.322 |
| D3 Growth ≠> D3 Inflation | 63.807 | 0.000 |
| D4 Growth ≠> D4 Inflation | 0.791 | 0.225 |
| D5 Growth ≠> D5 Inflation | 4.368 | 0.000 |
| D6 Growth ≠> D6 Inflation | 18.93 | 0.001 |
| S6 Growth ≠> S6 Inflation | 486.75 | 0.002 |
| D1 Inflation ≠>D1 Growth | 8.691 | 0.003 |
| D2 Inflation ≠>D2 Growth | 6.232 | 0.001 |
| D3 Inflation ≠>D3 Growth | 44.664 | 0.000 |
| D4 Inflation ≠>D4 Growth | 3.384 | 0.901 |
| D5 Inflation ≠>D5 Growth | 3.669 | 0.000 |
| D6 Inflation ≠>D6 Growth | 28.115 | 0.000 |
| S6 Inflation ≠>S6 Growth | 468.581 | 0.000 |
| Null Hypothesis | Test Value | p-Value |
|---|---|---|
| D1 Growth ≠> D1 Interest Rate | 15.582 | 0.000 |
| D2 Growth ≠> D2 Interest Rate | 1.614 | 0.204 |
| D3 Growth ≠> D3 Interest Rate | 65.679 | 0.000 |
| D4 Growth ≠> D4 Interest Rate | 0.033 | 0.855 |
| D5 Growth ≠> D5 Interest Rate | 5.258 | 0.022 |
| D6 Growth ≠> D6 Interest Rate | 73.964 | 0.000 |
| S6 Growth ≠> S6 Interest Rate | 32.174 | 0.000 |
| D1 Interest Rate ≠>D1 Growth | 8.224 | 0.004 |
| D2 Interest Rate ≠>D2 Growth | 0.112 | 0.739 |
| D3 Interest Rate ≠>D3 Growth | 85.655 | 0.000 |
| D4 Interest Rate ≠>D4 Growth | 29.848 | 0.000 |
| D5 Interest Rate ≠>D5 Growth | 7.022 | 0.008 |
| D6 Interest Rate ≠>D6 Growth | 166.030 | 0.000 |
| S6 Inflation Rate ≠>S6 Growth | 597.550 | 0.000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hayat, M.A.; Ghulam, H.; Batool, M.; Naeem, M.Z.; Ejaz, A.; Spulbar, C.; Birau, R. Investigating the Causal Linkages among Inflation, Interest Rate, and Economic Growth in Pakistan under the Influence of COVID-19 Pandemic: A Wavelet Transformation Approach. J. Risk Financial Manag. 2021, 14, 277. https://0-doi-org.brum.beds.ac.uk/10.3390/jrfm14060277
Hayat MA, Ghulam H, Batool M, Naeem MZ, Ejaz A, Spulbar C, Birau R. Investigating the Causal Linkages among Inflation, Interest Rate, and Economic Growth in Pakistan under the Influence of COVID-19 Pandemic: A Wavelet Transformation Approach. Journal of Risk and Financial Management. 2021; 14(6):277. https://0-doi-org.brum.beds.ac.uk/10.3390/jrfm14060277
Chicago/Turabian StyleHayat, Muhammad Azmat, Huma Ghulam, Maryam Batool, Muhammad Zahid Naeem, Abdullah Ejaz, Cristi Spulbar, and Ramona Birau. 2021. "Investigating the Causal Linkages among Inflation, Interest Rate, and Economic Growth in Pakistan under the Influence of COVID-19 Pandemic: A Wavelet Transformation Approach" Journal of Risk and Financial Management 14, no. 6: 277. https://0-doi-org.brum.beds.ac.uk/10.3390/jrfm14060277







