Analysis of Pressure and Production Transient Characteristics of Composite Reservoir with Moving Boundary
Abstract
:1. Introduction
2. Model Description
2.1. Physical Model and Assumptions
- (1)
- The reservoir is homogeneous, horizontal, uniform in thickness, and isotropic;
- (2)
- The original formation pressure (indicated by Pi) is evenly distributed, and the production rate of well is fixed after the well is opened;
- (3)
- The formation rocks and fluids are all slightly compressible;
- (4)
- The formation fluid conforms to the Darcy seepage law during seepage;
- (5)
- Wellbore storage and skin effects are accounted;
- (6)
- Gravity and capillary forces are ignored;
- (7)
- At the interface between the inner and outer zones, there is no flow loss and the formation pressure is not abrupt, and the interface moves with the propagation of mass wave;
- (8)
- The outer boundary condition is an infinite outer boundary;
- (9)
- The inner boundary expands to the outer region over time.
2.2. Factor Decomposition Model
2.2.1. Dimensionless Variables Definition
2.2.2. Governing Equations
2.2.3. Initial and Boundary Conditions
3. Model Solution
4. Results Analysis and Discussion
4.1. Flow Regimes Analysis
4.2. Pressure Parameter Sensitivity Analysis
4.2.1. Effect of Wellbore Storage
4.2.2. Effect of Skin Factor
4.2.3. Effect of Mobility Ratio
4.2.4. Effect of Diffusion Coefficient
4.2.5. Effect of Initial Interface Radius
4.2.6. Effect of Moving Boundary Moving Speed
4.3. Transient Production Parameter Sensitivity Analysis
4.3.1. Effect of Skin Factor
4.3.2. Effect of Mobility Ratio
4.3.3. Effect of Diffusion Coefficient
4.3.4. Effect of Initial Interface Radius
5. Conclusions
- (1)
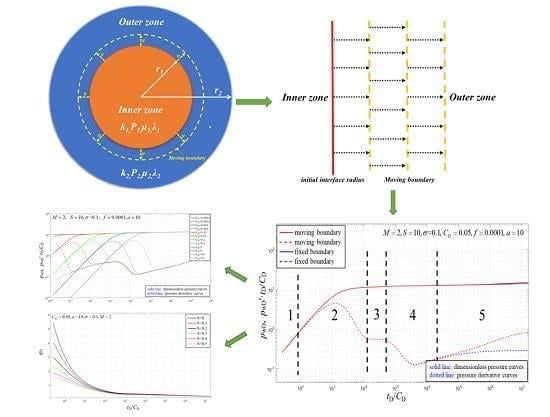
- The composite reservoir consists mainly of two zones: the inner zone and the outer zone. The pressure and pressure derivative curves include a total of five flow stages, including pure wellbore storage flow period, transition period of the pure wellbore storage flow to the inner zone radial flow, inner zone radial flow period, transition period of the radial flow of the inner zone to the radial flow of the moving boundary, and radial flow period of the moving boundary.
- (2)
- The wellbore storage coefficient increases, and the duration of the pure wellbore storage phase also increases. The larger the skin factor, the higher the peak of the pure wellbore storage flow to the inner zone radial flow transition phase. The greater the mobility ratio in the inner and outer zones, the higher the radial flow phase in the outer zone and the higher the upturn in the radial flow section of the moving boundary. The smaller the diffusion coefficient, the deeper the “concave” of the inner zone radial flow to the outer zone radial flow transition phase. The larger the initial interface radius, the longer the inner radial flow segment lasts. As the moving speed of the boundary increases, the duration of the radial flow period of the moving boundary becomes longer. Affected by the boundary, the pressure derivative and the pressure curves rise. It can be seen that the moving boundary causes pressure loss, which is not conducive to production.
- (3)
- For composite reservoir with moving boundary, as the skin factor increases, the initial production gets lower and lower. As the ratio of internal and external flow increases, the rate of decline is faster. The diffusion coefficient has little effect on the early production decline curves, but after a certain period of production, the production decreases rapidly as the diffusion coefficient increases. The interface radius has little effect on early production, but its influence increases as production time increases. If the mobility of the inner zone is greater than the mobility of the outer zone, the production decreases as the radius becomes larger, whereas the production increases as the radius becomes larger.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| pressure at a certain point in the formation, MPa | |
| ground flow, | |
| fluid viscosity, | |
| inner zone permeability, | |
| B | volume factor, |
| porosity, fraction | |
| wellbore radius, m | |
| r | distance from the left of the well, m |
| inner radius, m | |
| S | skin factor, fraction |
| h | oil layer thickness, m |
| original formation pressure, MPa | |
| a | initial interface radius, m |
| Q | production, |
| t | production time, d |
| diffusion coefficient ratio, fraction | |
| M | outer zone mobility ratio, fraction |
| A,B,C,D | coefficient, fraction |
| c | coefficient, fraction |
| total system compressibility, | |
| propagation time of the mass wave at the interface, d | |
| f | moving speed of the moving boundary |
| dimensionless production | |
| dimensionless pressure | |
| dimensionless time | |
| dimensionless radius | |
| dimensionless inner radius | |
| CD | dimensionless wellbore storage factor |
| dimensionless downhole pressure solution | |
| , | first type of virtual zero-order and first-order Bessel functions |
| , | second type of virtual zero-order and first-order Bessel functions |
| Dim. pressure | dimensionless pressure |
Subscript
| D | dimensionless |
Superscript
| Laplace transform |
References
- Loucks, T.; Guerrero, E. Pressure drop in a composite reservoir. Soc. Pet. Eng. J. 1961, 1, 170–176. [Google Scholar] [CrossRef]
- Carter, R. Pressure behavior of a limited circular composite reservoir. Soc. Pet. Eng. J. 1966, 6, 328–334. [Google Scholar] [CrossRef] [Green Version]
- Ambastha, A.; McLeroy, P.; Grader, A. Effects of a partially communicating fault in a composite reservoir on transient pressure testing. SPE Form. Eval. 1989, 4, 210–218. [Google Scholar] [CrossRef]
- Chu, W.-C.; Shank, G.D. A new model for a fractured well in a radial, composite reservoir (includes associated papers 27919, 28665 and 29212). SPE Form. Eval. 1993, 8, 225–232. [Google Scholar] [CrossRef]
- Escobar, F.-H.; Martínez, J.-A.; Montealegre-Madero, M. Pressure and pressure derivate analysis for a well in a radial composite reservoir with a non-newtonian/newtonian interface. Ct F Cienc. Tecnol. Y Futuro 2010, 4, 33–42. [Google Scholar]
- Zhang, L.-H.; Zhao, Y.; Liu, Q. Well-test-analysis and applications of source functions in a bi-zonal composite gas reservoir. Pet. Sci. Technol. 2014, 32, 965–973. [Google Scholar] [CrossRef]
- Liu, Q.; Lu, H.; Li, L.; Mu, A. Study on characteristics of well-test type curves for composite reservoir with sealing faults. Petroleum 2018, 4, 309–317. [Google Scholar] [CrossRef]
- Razminia, K.; Razminia, A.; Trujilo, J.J. Analysis of radial composite systems based on fractal theory and fractional calculus. Signal Process. 2015, 107, 378–388. [Google Scholar] [CrossRef]
- Meng, F.; Lei, Q.; He, D.; Yan, H.; Jia, A.; Deng, H.; Xu, W. Production performance analysis for deviated wells in composite carbonate gas reservoirs. J. Nat. Gas Sci. Eng. 2018, 56, 333–343. [Google Scholar] [CrossRef]
- Wu, M.; Ding, M.; Yao, J.; Li, C.; Huang, Z.; Xu, S. Production-Performance Analysis of Composite Shale-Gas Reservoirs by the Boundary-Element Method. SPE Reserv. Eval. Eng. 2018, 22. [Google Scholar] [CrossRef] [Green Version]
- Wu, M.; Ding, M.; Yao, J.; Xu, S.; Li, L.; Li, X. Pressure transient analysis of multiple fractured horizontal well in composite shale gas reservoirs by boundary element method. J. Pet. Sci. Eng. 2018, 162, 84–101. [Google Scholar] [CrossRef]
- Gringarten, A.C.; Ramey, H.J., Jr. The use of source and Green’s functions in solving unsteady-flow problems in reservoirs. Soc. Pet. Eng. J. 1973, 13, 285–296. [Google Scholar] [CrossRef]
- Ozkan, E.; Raghavan, R. Some New Solutions to Solve Problems in Well Test Analysis: Part 2—Computational Considerations and Applications; Society of Petroleum Engineers: Richardson, TX, USA, 1988; pp. 1–67. [Google Scholar]
- Cheng, C.; Chau, K.; Sun, Y.; Lin, J. Long-term prediction of discharges in Manwan Reservoir using artificial neural network models. In International Symposium on Neural Networks; Springer: Berlin, Germany, 2005; Volume 3498, pp. 1040–1045. [Google Scholar]
- Chen, W.; Chau, K. Intelligent manipulation and calibration of parameters for hydrological models. Int. J. Eniron. Pollut. 2006, 28, 432–447. [Google Scholar] [CrossRef] [Green Version]
- Chau, K.-W. An ontology-based knowledge management system for flow and water quality modeling. Adv. Eng. Softw. 2007, 38, 172–181. [Google Scholar] [CrossRef] [Green Version]
- Taormina, R.; Chau, K.-W.; Sethi, R. Artificial neural network simulation of hourly groundwater levels in a coastal aquifer system of the Venice lagoon. Eng. Appl. Artif. Intell. 2012, 25, 1670–1676. [Google Scholar] [CrossRef] [Green Version]
- Mohebbi, R.; Delouei, A.A.; Jamali, A.; Izadi, M.; Mohamad, A.A. Pore-scale simulation of non-Newtonian power-law fluid flow and forced convection in partially porous media: Thermal lattice Boltzmann method. Phys. A Stat. Mech. Appl. 2019, 525, 642–656. [Google Scholar] [CrossRef]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids, 2nd ed.; Clarendon Press: Oxford, UK, 1959. [Google Scholar]
- Hurst, W. Interference between Oil Fields; Society of Petroleum Engineers: Richardson, TX, USA, 1960; Volume 219, pp. 175–192. [Google Scholar]
- Closmann, P.; Ratliff, N. Calculation of transient oil production in a radial composite reservoir. Soc. Pet. Eng. J. 1967, 7, 355–358. [Google Scholar] [CrossRef]
- Bixel, H.; van Poollen, H. Pressure drawdown and buildup in the presence of radial discontinuities. Soc. Pet. Eng. J. 1967, 7, 301–309. [Google Scholar] [CrossRef]
- Merrill, L., Jr.; Kazemi, H.; Gogarty, W.B. Pressure falloff analysis in reservoirs with fluid banks. J. Pet. Technol. 1974, 26, 809–818. [Google Scholar] [CrossRef]
- Ambastha, A. Practical Aspects of Well Test Analysis under composite reservoir situations. J. Can. Pet. Technol. 1995, 34. [Google Scholar] [CrossRef]
- Satman, A. An analytical study of interference in composite reservoirs. Soc. Pet. Eng. J. 1985, 25, 281–290. [Google Scholar] [CrossRef]
- Olarewaju, J.; Lee, W.J. A comprehensive application of a composite reservoir model to pressure transient analysis. In Proceedings of the SPE California Regional Meeting, Ventura, CA, USA, 8–10 April 1987; Society of Petroleum Engineers: Richardson, TX, USA, 1987; pp. 1–17. [Google Scholar]
- Boussalem, R.; Djebbar, T.; Escobar, F.H. Effect of mobility ratio on the pressure and pressure derivative of wells in closed composite reservoirs. In Proceedings of the SPE western regional/AAPG pacific section joint meeting, Anchorage, AK, USA, 20–22 May 2002; Society of Petroleum Engineers: Richardson, TX, USA, 2002; pp. 1–6. [Google Scholar]
- Issaka, M.B. Well Test Analysis for Composite Reservoirs in Various Flow Geometries. Ph.D. Thesis, University of Alberta, Edmonton, AB, Canada, 1996; pp. 1–128. [Google Scholar]
- Issaka, M.; Ambastha, A. A generalized pressure derivative analysis for composite reservoirs. J. Can. Pet. Technol. 1999, 38. [Google Scholar] [CrossRef]
- Ambastha, A.; Ramey, H., Jr. Pressure transient analysis for a three-region composite reservoir. In Proceedings of the SPE Rocky Mountain Regional Meeting, Casper, WY, USA, 18–21 May 1992; Society of Petroleum Engineers: Richardson, TX, USA, 1992; pp. 1–10. [Google Scholar]
- Jordan, C.; Mattar, L. Comparison of pressure transient behaviour of composite and two-layered reservoirs. J. Can. Pet. Technol. 2002, 41. [Google Scholar] [CrossRef]
- Rahman, N.; Miller, M.D.; Mattar, L. Analytical solution to the transient-flow problems for a well located near a finite-conductivity fault in composite reservoirs. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 5–8 October 2003; Society of Petroleum Engineers: Richardson, TX, USA, 2003; pp. 1–13. [Google Scholar]
- Wang, X.-D.; Zhou, Y.-F.; Luo, W.-J. A study on transient fluid flow of horizontal wells in dual-permeability media. J. Hydrodyn. 2010, 22, 44–50. [Google Scholar] [CrossRef]
- Brohi, I.G.; Pooladi-Darvish, M.; Aguilera, R. Modeling fractured horizontal wells as dual porosity composite reservoirs-application to tight gas, shale gas and tight oil cases. In Proceedings of the SPE Western North American Region Meeting, Anchorage, AK, USA, 7–11 May 2011; Society of Petroleum Engineers: Richardson, TX, USA, 2011; pp. 1–22. [Google Scholar]
- Nie, R.-S.; Guo, J.; Jia, Y.; Zhu, S.; Rao, Z.; Zhang, C. New modelling of transient well test and rate decline analysis for a horizontal well in a multiple-zone reservoir. J. Geophys. Eng. 2011, 8, 464–476. [Google Scholar] [CrossRef]
- Wang, X.-L.; Fan, X.; He, Y.; Nie, R.; Huang, Q. A nonlinear model for fluid flow in a multiple-zone composite reservoir including the quadratic gradient term. J. Geophys. Eng. 2013, 10, 045009. [Google Scholar] [CrossRef]
- Gu, D.; Ding, D.; Gao, Z.; Tian, L.; Liu, L.; Xiao, C. A fractally fractional diffusion model of composite dual-porosity for multiple fractured horizontal wells with stimulated reservoir volume in tight gas reservoirs. J. Pet. Sci. Eng. 2019, 173, 53–68. [Google Scholar] [CrossRef]
- Olarewaju, J.; Lee, W. An analytical model for composite reservoirs produced at either constant bottomhole pressure or constant rate. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 27–30 September 1987; Society of Petroleum Engineers: Richardson, TX, USA, 1987; pp. 1–14. [Google Scholar]
- Wang, H.; Zhang, L. A boundary element method applied to pressure transient analysis of geometrically complex gas reservoirs. In Proceedings of the Latin American and Caribbean Petroleum Engineering Conference, Cartagena, Colombia, 31 May–3 June 2009; Society of Petroleum Engineers: Richardson, TX, USA, 2009; pp. 1–12. [Google Scholar]
- El-Khatib, N.A. Transient pressure behavior of composite reservoirs with moving boundaries. In Proceedings of the Middle East Oil Show and Conference, Bahrain, 20–23 February 1999; Society of Petroleum Engineers: Richardson, TX, USA, 1999; pp. 1–15. [Google Scholar]
- Widder, D.V. Laplace Transform (PMS-6); Princeton University Press: Princeton, NJ, USA, 2015; pp. 1–390. [Google Scholar]
- Magnus, W.; Oberhettinger, F.; Soni, R.P. Formulas and Theorems for the Special Functions of Mathematical Physics; Springer Science & Business Media: Berlin, Germany, 2013; pp. 1–500. [Google Scholar]
- Stehfest, H. Algorithm 368: Numerical inversion of Laplace transforms [D5]. Commun. ACM 1970, 13, 47–49. [Google Scholar] [CrossRef]













© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Z.; Yang, X.; Jin, Y.; Shi, S.; Wu, M. Analysis of Pressure and Production Transient Characteristics of Composite Reservoir with Moving Boundary. Energies 2020, 13, 34. https://0-doi-org.brum.beds.ac.uk/10.3390/en13010034
Sun Z, Yang X, Jin Y, Shi S, Wu M. Analysis of Pressure and Production Transient Characteristics of Composite Reservoir with Moving Boundary. Energies. 2020; 13(1):34. https://0-doi-org.brum.beds.ac.uk/10.3390/en13010034
Chicago/Turabian StyleSun, Zhixue, Xugang Yang, Yanxin Jin, Shubin Shi, and Minglu Wu. 2020. "Analysis of Pressure and Production Transient Characteristics of Composite Reservoir with Moving Boundary" Energies 13, no. 1: 34. https://0-doi-org.brum.beds.ac.uk/10.3390/en13010034