Digital Image Correlation of 2D X-ray Powder Diffraction Data for Lattice Strain Evaluation
Abstract
:1. Introduction
2. The XRD-DIC Approach
2.1. DIC Introduction
2.2. DIC Implementation
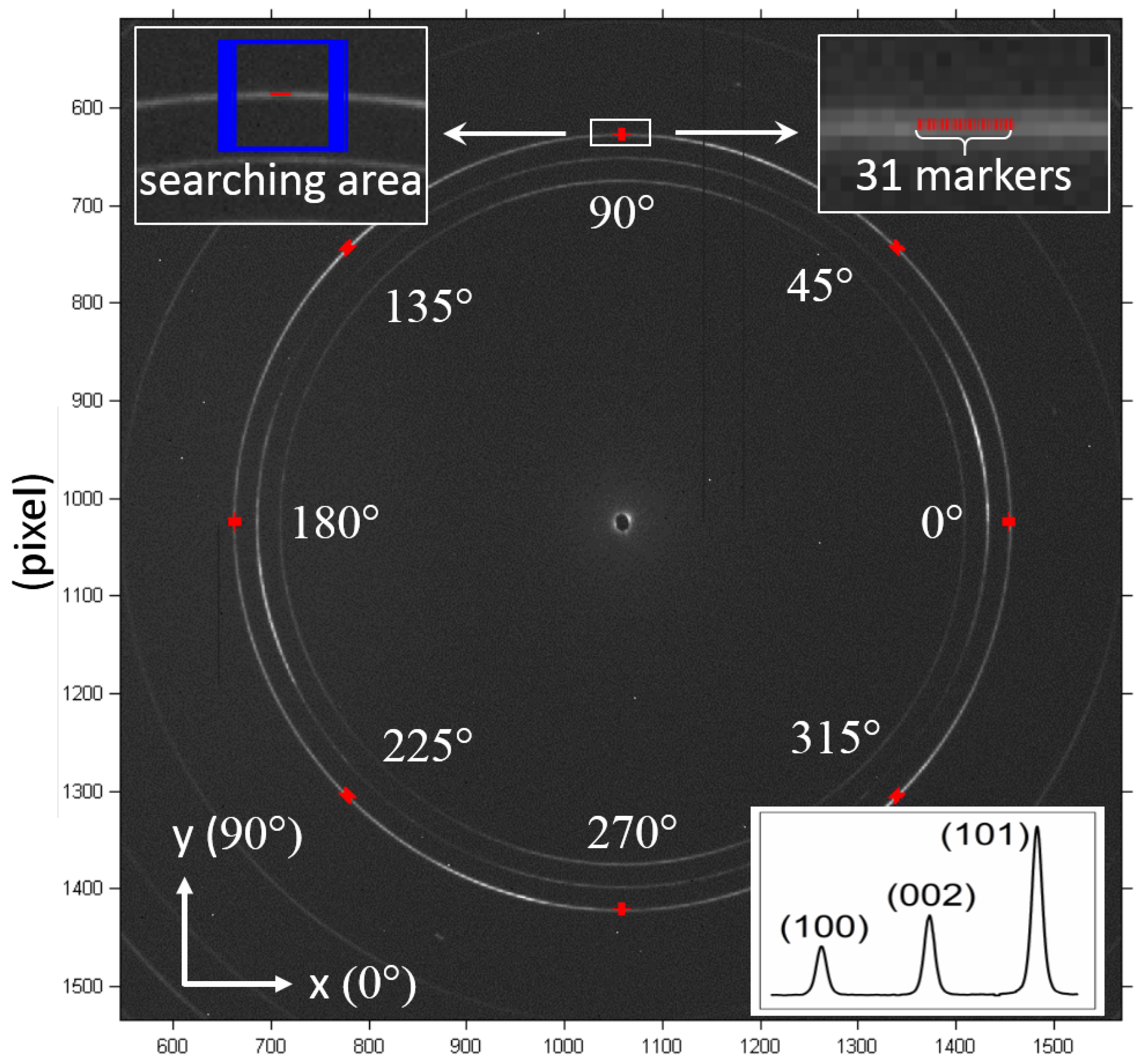
2.2.1. Pre-Processing
2.2.2. Tracking and Post-Processing
2.3. Advantages of XRD-DIC
3. Material and Experiment
3.1. Three-Point Bending
3.2. XRD Experiment
3.3. DIC Analysis
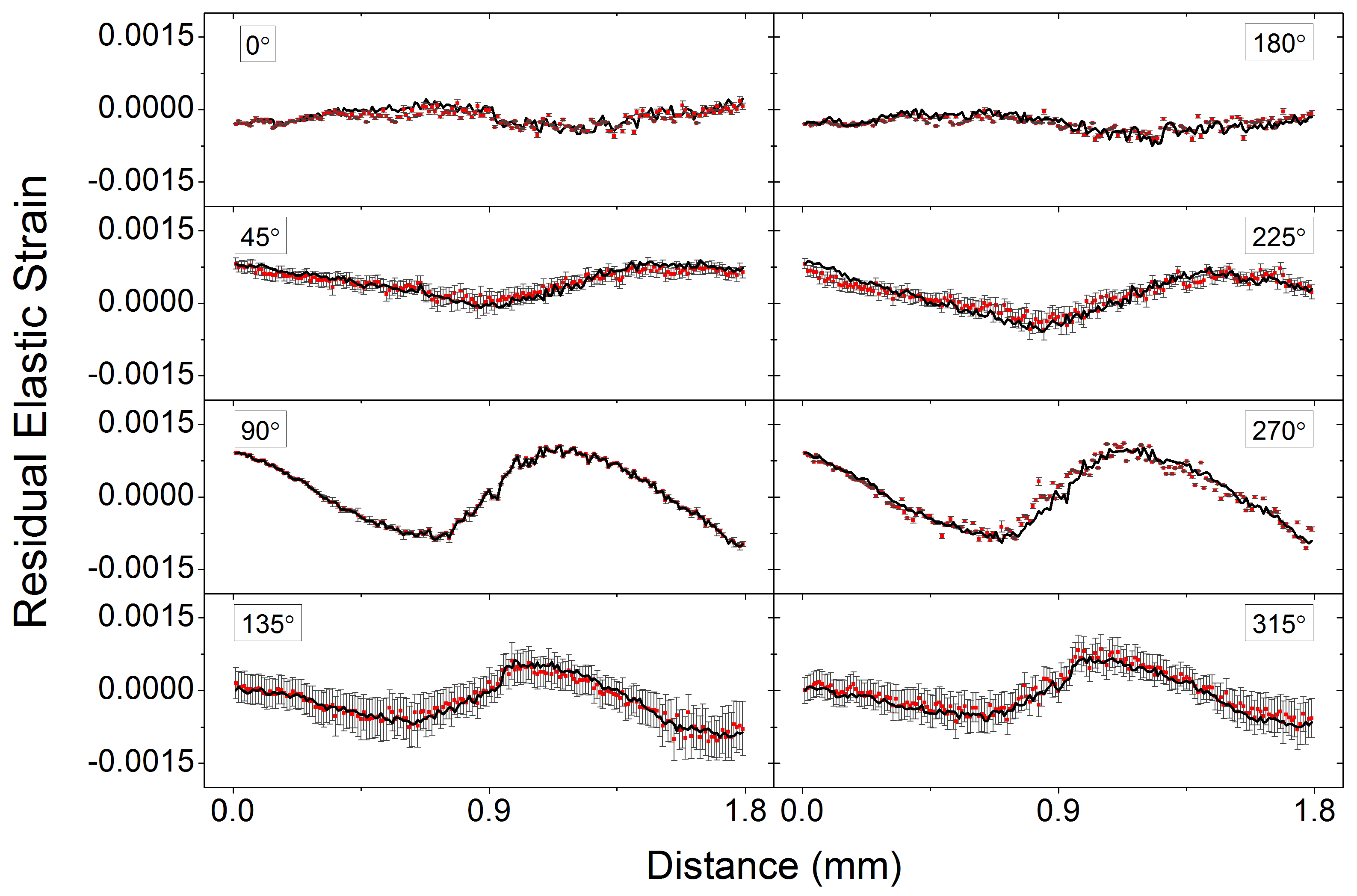
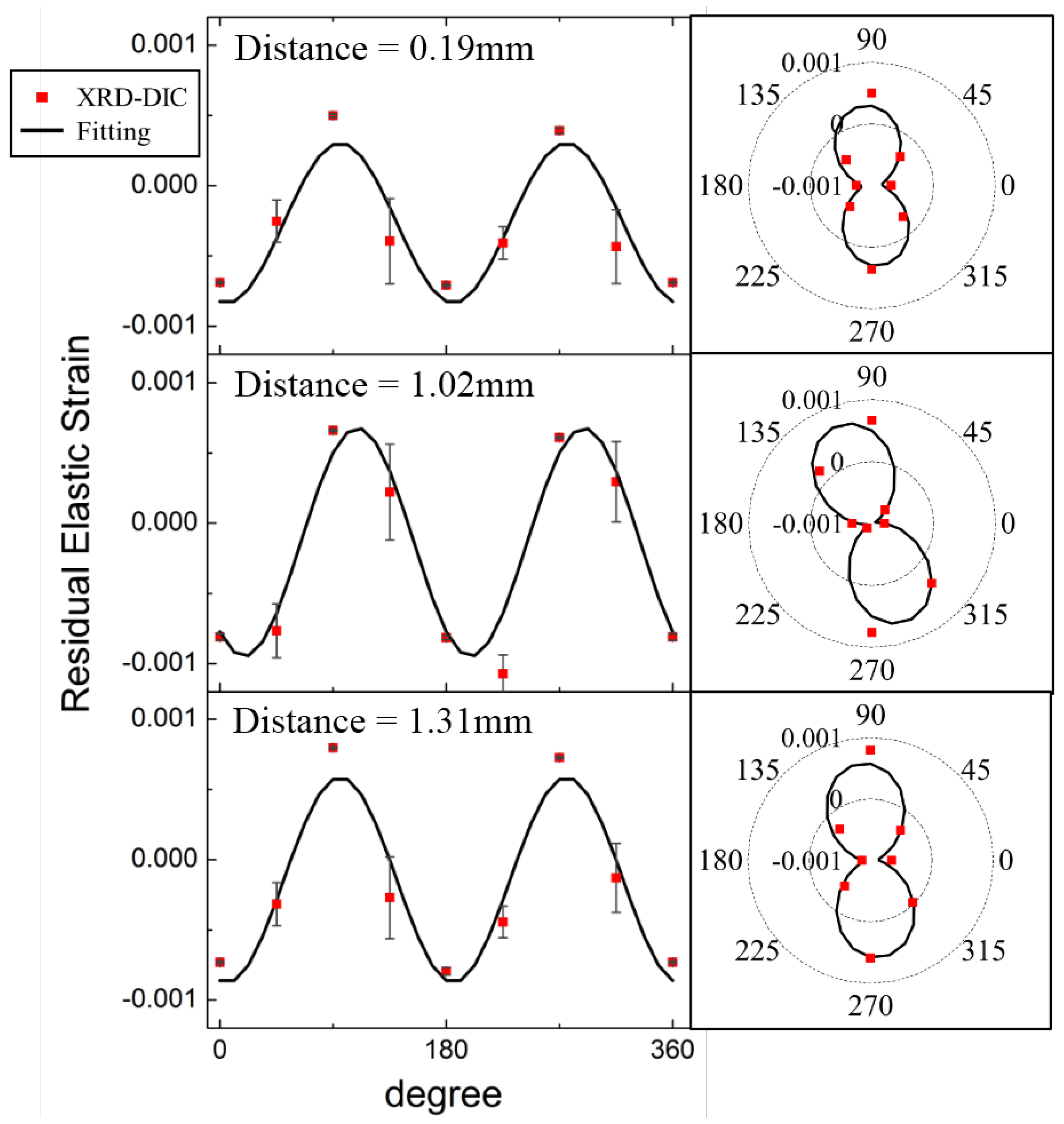
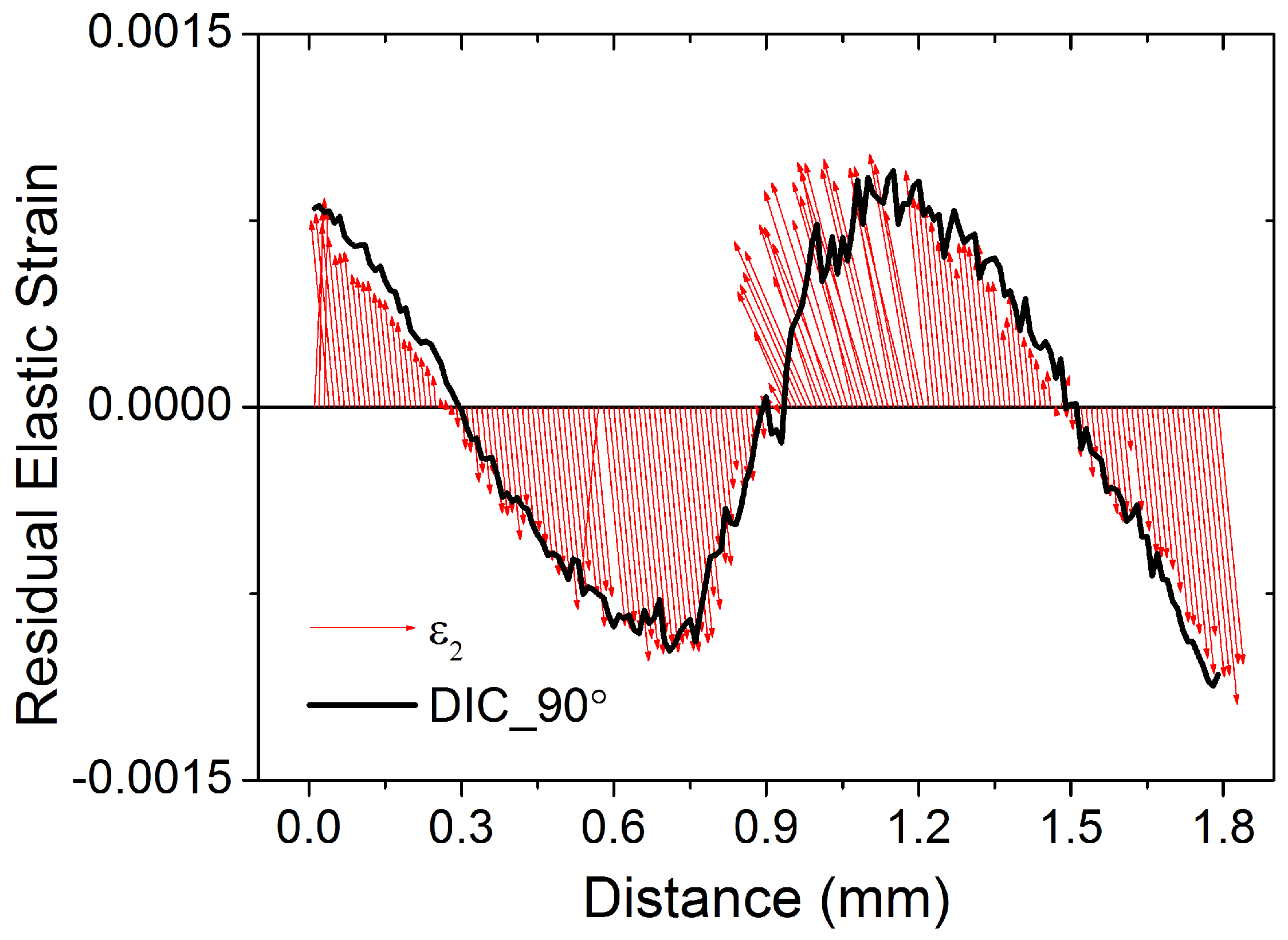
4. Results and Discussion
5. Conclusions and Outlook
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mishurova, T.; Cabeza, S.; Artzt, K.; Haubrich, J.; Klaus, M.; Genzel, C.; Requena, G.; Bruno, G. An assessment of subsurface residual stress analysis in SLM Ti-6Al-4V. Materials 2017, 10, 348. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Song, W.; Bleck, W. Investigation of the Microstructure Evolution in a Fe-17Mn-1.5 Al-0.3 C Steel via In Situ Synchrotron X-ray Diffraction during a Tensile Test. Materials 2017, 10, 1129. [Google Scholar]
- Yi, S.B.; Davies, C.; Brokmeier, H.G.; Bolmaro, R.; Kainer, K.; Homeyer, J. Deformation and texture evolution in AZ31 magnesium alloy during uniaxial loading. Acta Mater. 2006, 54, 549–562. [Google Scholar] [CrossRef]
- Bohr, J.; Feidenhans, R.; Nielsen, M.; Toney, M.; Johnson, R.; Robinson, I. Model-independent structure determination of the InSb (111) 2 × 2 surface with use of synchrotron X-ray diffraction. Phys. Rev. Lett. 1985, 54, 1275. [Google Scholar] [CrossRef] [PubMed]
- Guss, J.M.; Merritt, E.A.; Phizackerley, R.P.; Hedman, B.; Murata, M.; Hodgson, K.O.; Freeman, H.C. Phase determination by multiple-wavelength X-ray diffraction: Crystal structure of a basic “blue” copper protein from cucumbers. Science 1988, 241, 806–811. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.Q.; McBreen, J.; Yoon, W.S.; Grey, C.P. Crystal structure changes of LiMn 0.5 Ni 0.5 O 2 cathode materials during charge and discharge studied by synchrotron based in situ XRD. Electrochem. Commun. 2002, 4, 649–654. [Google Scholar] [CrossRef]
- Shin, H.C.; Park, S.B.; Jang, H.; Chung, K.Y.; Cho, W.I.; Kim, C.S.; Cho, B.W. Rate performance and structural change of Cr-doped LiFePO 4/C during cycling. Electrochim. Acta 2008, 53, 7946–7951. [Google Scholar] [CrossRef]
- Langford, J.I.; Louer, D. Powder diffraction. Rep. Prog. Phys. 1996, 59, 131. [Google Scholar] [CrossRef]
- Daum, R.; Chu, Y.; Motta, A. Identification and quantification of hydride phases in Zircaloy-4 cladding using synchrotron X-ray diffraction. J. Nucl. Mater. 2009, 392, 453–463. [Google Scholar] [CrossRef]
- Almer, J.; Lienert, U.; Peng, R.L.; Schlauer, C.; Odén, M. Strain and texture analysis of coatings using high-energy X-rays. J. Appl. Phys. 2003, 94, 697–702. [Google Scholar] [CrossRef]
- Xie, M. X-ray and Neutron Diffraction analysis and Fem Modelling of Stress and Texture Evolution in cubic Polycrystals. Ph.D. Thesis, University of Oxford, Oxford, UK, 2014. [Google Scholar]
- Shi, X.; Ghose, S.; Dooryhee, E. Performance calculations of the X-ray powder diffraction beamline at NSLS-II. J. Synchrotron Radiat. 2013, 20, 234–242. [Google Scholar] [CrossRef] [PubMed]
- Wanner, A.; Dunand, D.C. Synchrotron X-ray study of bulk lattice strains in externally loaded Cu-Mo composites. Metall. Mater. Trans. A 2000, 31, 2949–2962. [Google Scholar] [CrossRef]
- Poshadel, A.; Dawson, P.; Johnson, G. Assessment of deviatoric lattice strain uncertainty for polychromatic X-ray microdiffraction experiments. J. Synchrotron Radiat. 2012, 19, 237–244. [Google Scholar] [CrossRef] [PubMed]
- Hutchinson, J. Plastic stress and strain fields at a crack tip. J. Mech. Phys. Solids 1968, 16, 337–342. [Google Scholar] [CrossRef]
- Hill, R. The Mathematical Theory of Plasticity; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Macherauch, E. Introduction to Residual Stress. In Advances in Surface Treatments: Technology-Application-Effect; A Niku-Lari; Pergamon Press: Oxford, UK, 1986; Volume 4, pp. 1–36. [Google Scholar]
- Zhang, S.Y. High Energy White Beam X-ray Diffraction Studies of Strains in Engineering Materials and Components. Ph. D. Thesis, University of Oxford, Oxford, UK, 2008. [Google Scholar]
- Rendler, N.; Vigness, I. Hole-drilling strain-gage method of measuring residual stresses. Exp. Mech. 1966, 6, 577–586. [Google Scholar] [CrossRef]
- Sebastiani, M.; Eberl, C.; Bemporad, E.; Pharr, G.M. Depth-resolved residual stress analysis of thin coatings by a new FIB–DIC method. Mater. Sci. Eng. A 2011, 528, 7901–7908. [Google Scholar] [CrossRef]
- Korsunsky, A.M.; Sebastiani, M.; Bemporad, E. Residual stress evaluation at the micrometer scale: Analysis of thin coatings by FIB milling and digital image correlation. Surf. Coat. Technol. 2010, 205, 2393–2403. [Google Scholar] [CrossRef]
- Cheng, W.; Finnie, I. Residual Stress Measurement and the Slitting Method; Springer Science & Business Media: New York, NY, USA, 2007. [Google Scholar]
- Treuting, R.; Read, W., Jr. A mechanical determination of biaxial residual stress in sheet materials. J. Appl. Phys. 1951, 22, 130–134. [Google Scholar] [CrossRef]
- Window, A.L.; Holister, G.S. Strain Gauge Technology; Applied Science Publishers: London, UK, 1982. [Google Scholar]
- Cullity, B.D. Elements of X-ray Diffraction; Addison-Wesley Publishing Company, Inc.: Reading, MA, USA, 1956. [Google Scholar]
- Korsunsky, A.M.; Wells, K.E.; Withers, P.J. Mapping two-dimensional state of strain using synchroton X-ray diffraction. Scr. Mater. 1998, 39, 1705–1712. [Google Scholar] [CrossRef]
- Comley, A.; Maddox, B.; Rudd, R.; Prisbrey, S.; Hawreliak, J.; Orlikowski, D.; Peterson, S.; Satcher, J.; Elsholz, A.; Park, H.S. Strength of shock-loaded single-crystal tantalum [100] determined using in situ broadband X-ray Laue diffraction. Phys. Rev. Lett. 2013, 110, 115501. [Google Scholar] [CrossRef] [PubMed]
- Daniels, J.; Drakopoulos, M. High-energy X-ray diffraction using the Pixium 4700 flat-panel detector. J. Synchrotron Radiat. 2009, 16, 463–468. [Google Scholar] [CrossRef] [PubMed]
- He, B.B. Two-Dimensional X-ray Diffraction; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]
- Petit, J.; Bornert, M.; Hofmann, F.; Robach, O.; Micha, J.; Ulrich, O.; Le Bourlot, C.; Faurie, D.; Korsunsky, A.; Castelnau, O. Combining Laue microdiffraction and digital image correlation for improved measurements of the elastic strain field with micrometer spatial resolution. Procedia IUTAM 2012, 4, 133–143. [Google Scholar] [CrossRef]
- Zhang, F.; Castelnau, O.; Bornert, M.; Petit, J.; Marijon, J.; Plancher, E. Determination of deviatoric elastic strain and lattice orientation by applying digital image correlation to Laue microdiffraction images: The enhanced Laue-DIC method. J. Appl. Crystallogr. 2015, 48, 1805–1817. [Google Scholar] [CrossRef]
- Pan, B.; Qian, K.; Xie, H.; Asundi, A. Two-dimensional digital image correlation for in-plane displacement and strain measurement: A review. Meas. Sci. Technol. 2009, 20, 062001. [Google Scholar] [CrossRef]
- Lunt, A.J.; Baimpas, N.; Salvati, E.; Dolbnya, I.P.; Sui, T.; Ying, S.; Zhang, H.; Kleppe, A.K.; Dluhoš, J.; Korsunsky, A.M. A state-of-the-art review of micron-scale spatially resolved residual stress analysis by FIB-DIC ring-core milling and other techniques. J. Strain Anal. Eng. Design 2015, 50, 426–444. [Google Scholar] [CrossRef]
- Yates, J.; Zanganeh, M.; Tai, Y. Quantifying crack tip displacement fields with DIC. Eng. Fract. Mech. 2010, 77, 2063–2076. [Google Scholar] [CrossRef]
- Abanto-Bueno, J.; Lambros, J. Investigation of crack growth in functionally graded materials using digital image correlation. Eng. Fract. Mech. 2002, 69, 1695–1711. [Google Scholar] [CrossRef]
- McCormick, N.; Lord, J. Digital image correlation. Mater. Today 2010, 13, 52–54. [Google Scholar] [CrossRef]
- Kujawińska, M.; Malesa, M.; Malowany, K. Measuring structural displacements with digital image correlation. SPIE Newsroom 2013, 2013, 1–4. [Google Scholar] [CrossRef]
- Senn, M.; Eberl, C. Digital Image Correlation and Tracking, 2015. Available online: https://cn.mathworks.com/matlabcentral/fileexchange/50994-digital-image-correlation-and-tracking?requestedDomain=true (accessed on 1 February 2018).
- Lunt, A.J.; Korsunsky, A.M. A review of micro-scale focused ion beam milling and digital image correlation analysis for residual stress evaluation and error estimation. Surf. Coat. Technol. 2015, 283, 373–388. [Google Scholar] [CrossRef]
- Lunt, A.J.; Salvati, E.; Ma, L.; Dolbyna, I.P.; Neo, T.K.; Korsunsky, A.M. Full in-plane strain tensor analysis using the microscale ring-core FIB milling and DIC approach. J. Mech. Phys. Solids 2016, 94, 47–67. [Google Scholar] [CrossRef]
- Fong, K.S.; Atsushi, D.; Jen, T.M.; Chua, B.W. Effect of Deformation and Temperature Paths in Severe Plastic Deformation Using Groove Pressing on Microstructure, Texture, and Mechanical Properties of AZ31-O. J. Manuf. Sci. Eng. 2015, 137, 051004. [Google Scholar] [CrossRef]
- Liu, W.; Wu, G.; Zhai, C.; Ding, W.; Korsunsky, A.M. Grain refinement and fatigue strengthening mechanisms in as-extruded Mg–6Zn–0.5 Zr and Mg–10Gd–3Y–0.5 Zr magnesium alloys by shot peening. Int. J. Plast. 2013, 49, 16–35. [Google Scholar] [CrossRef]
- Estrin, Y.; Vinogradov, A. Extreme grain refinement by severe plastic deformation: A wealth of challenging science. Acta Mater. 2013, 61, 782–817. [Google Scholar] [CrossRef]
- Mathworks. Digital Image Correlation and Tracking, 2017. Available online: https://uk.mathworks.com/help/images/index.html (accessed on 1 February 2018).
- Hammersley, A.; Svensson, S.; Hanfland, M.; Fitch, A.; Hausermann, D. Two-dimensional detector software: From real detector to idealised image or two-theta scan. Int. J. High Press. Res. 1996, 14, 235–248. [Google Scholar] [CrossRef]
- Matlab Version R2016a; The MathWorks Inc.: Natick, MA, USA, 2016.


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Sui, T.; Salvati, E.; Daisenberger, D.; Lunt, A.J.G.; Fong, K.S.; Song, X.; Korsunsky, A.M. Digital Image Correlation of 2D X-ray Powder Diffraction Data for Lattice Strain Evaluation. Materials 2018, 11, 427. https://0-doi-org.brum.beds.ac.uk/10.3390/ma11030427
Zhang H, Sui T, Salvati E, Daisenberger D, Lunt AJG, Fong KS, Song X, Korsunsky AM. Digital Image Correlation of 2D X-ray Powder Diffraction Data for Lattice Strain Evaluation. Materials. 2018; 11(3):427. https://0-doi-org.brum.beds.ac.uk/10.3390/ma11030427
Chicago/Turabian StyleZhang, Hongjia, Tan Sui, Enrico Salvati, Dominik Daisenberger, Alexander J. G. Lunt, Kai Soon Fong, Xu Song, and Alexander M. Korsunsky. 2018. "Digital Image Correlation of 2D X-ray Powder Diffraction Data for Lattice Strain Evaluation" Materials 11, no. 3: 427. https://0-doi-org.brum.beds.ac.uk/10.3390/ma11030427





