Toward Better Control of Inclusion Cleanliness in a Gas Stirred Ladle Using Multiscale Numerical Modeling
Abstract
:1. Introduction
2. Methods and Computational Models
2.1. Mesoscale Modeling of Inclusion Behavior
2.1.1. Aggregation Kinetics
2.1.2. Aggregate Restructuring
2.2. Macroscale Modeling of the Steel Ladle
2.2.1. Hydrodynamic Simulation
2.2.2. Population Balance Modeling (PBM)
3. Results and Discussion
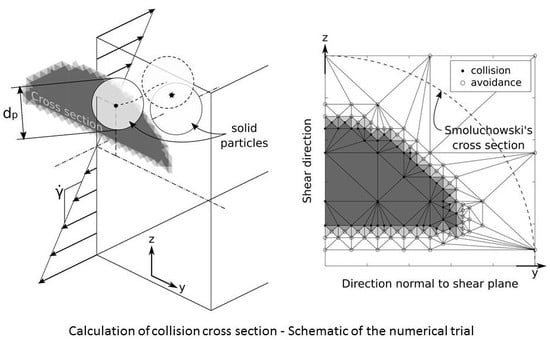
3.1. Calculation of the Shear Rate Collision Kernel
3.2. Restructuring of Aggregates in a Pure Shear Flow
3.3. Macroscale Simulation
3.3.1. Hydrodynamic Validation
3.3.2. Evolution of the Inclusion Population in the Successive High and Low Stirring Steps
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Greek letters | |
| α | volume fraction |
| shear rate (s−1) | |
| η | collision efficiency |
| µ | dynamic viscosity of the liquid metal (Pa·s) |
| kinematic viscosity of the liquid metal (m2·s−1) | |
| Archimedes’ constant | |
| Latin letters | |
| B | population balance birth kernel (# m−3·s−1) |
| D | population balance death kernel (# m−3·s−1) |
| d | diameter (m) |
| F | force (N) |
| N | number of inclusions per unit volume of liquid metal (# m−3) |
| f | frequency (s−1) |
| S | gravity separation term in PBE (# m−3·s−1) |
| surface or surface area (m2) | |
| u | fluid velocity (m·s−1) |
| V | volume (m3) |
| y | abscissa in the direction normal to the shear plane (m) |
| z | abscissa in the direction along the velocity gradient (m) |
| Z | collision frequency (m−3·s−1) |
| Subscripts | |
| A | relative to the aggregation mechanism |
| b | relative to gas bubbles and flotation |
| Col | relative to the actual collision cross section |
| drag | relative to the action of the liquid phase on the solids |
| i, j | discrete size classes in the population balance equation |
| g, l | gas or liquid phase |
| ladle | relative to the steel ladle |
| p | particle property |
| Smo | relative to Smoluchowski’s collision cross section |
| Compound | |
| shear-based particle Reynolds number defined in Equation (1) | |
References
- Zhang, L.; Thomas, B.G. State of the art in evaluation and control of steel cleanliness. ISIJ Int. 2003, 43, 271–291. [Google Scholar] [CrossRef]
- Kato, T.; Shimasaki, S.; Taniguchi, S. Water model experiments for hydrodynamic forces acting on inclusion particles in molten metal under turbulent condition. In Jim Evans Honorary Symposium: Proceedings of the Symposium Sponsored by the Light Metals Division of The Minerals, Metals and Materials Society (TMS); Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Xie, Y.; Orsten, S.; Oeters, F. Behaviour of bubbles at gas blowing into liquid woods metal. ISIJ Int. 1992, 32, 66–75. [Google Scholar] [CrossRef]
- Mendez, C.G.; Nigro, N.; Cardona, A. Drag and non-drag force influences in numerical simulations of metallurgical ladles. J. Mater. Process. Technol. 2005, 160, 296–305. [Google Scholar] [CrossRef]
- Liu, H.; Qi, Z.; Xu, M. Numerical Simulation of Fluid Flow and Interfacial Behavior in Three-phase Argon-Stirred Ladles with One Plug and Dual Plugs. Steel Res. Int. 2011, 82, 440–458. [Google Scholar] [CrossRef]
- Madan, M.; Satish, D.; Mazumdar, D. Modeling of mixing in ladies fitted with dual plugs. ISIJ Int. 2005, 45, 677–685. [Google Scholar] [CrossRef]
- De Felice, V.; Daoud, I.L.A.; Dussoubs, B.; Jardy, A.; Bellot, J.P. Numerical modelling of inclusion behavior in a gas-stirred ladle. ISIJ Int. 2012, 52, 1274–1281. [Google Scholar] [CrossRef]
- Li, L.; Liu, Z.; Li, B.; Matssra, H.; Tsukihashi, F. Water Model and CFD-PBM Coupled Model of Gas-Liquid-Slag Three-Phase Flow in Ladle Metallurgy. ISIJ Int. 2015, 55, 1337–1346. [Google Scholar] [CrossRef] [Green Version]
- Bellot, J.P.; De Felice, V.; Dussoubs, B.; Jardy, A.; Hans, S. Coupling of a CFD and a PBE calculations to simulate the behavior of an inclusion population in a gas-stirred ladle. Met. Trans. B 2014, 45, 13–21. [Google Scholar] [CrossRef]
- Kwon, Y.-J.; Zhang, J.; Lee, H.-G. A CFD-based Nucleation-growth-removal Model for Inclusion Behavior in a Gas-agitated Ladle during Molten Steel Deoxidation. ISIJ Int. 2008, 48, 891–900. [Google Scholar] [CrossRef] [Green Version]
- Claudotte, L.; Rimbert, N.; Gardin, P.; Simonnet, M.; Lehmann, J.; Oesterle, B. A Multi-QMOM Framework to Describe Multi-Component Agglomerates in Liquid Steel. AIChE J. 2010, 56, 2347–2355. [Google Scholar] [CrossRef]
- Lei, H.; Nakajima, K.; He, J.-C. Mathematical Model for Nucleation, Ostwald Ripening and Growth of Inclusion in Molten Steel. ISIJ Int. 2010, 50, 1735–1745. [Google Scholar] [CrossRef] [Green Version]
- Eggels, J.G.M.; Somers, J.A. Numerical simulation of free convective flow using the lattice-Boltzmann scheme. Int. J. Heat Fluid Flow 1995, 16, 357–364. [Google Scholar] [CrossRef]
- Sungkorn, R.; Derksen, J.J. Simulations of dilute sedimenting suspensions at finite-particle Reynolds numbers. Phys. Fluids 2012, 24, 123303. [Google Scholar] [CrossRef]
- Niu, X.D.; Shu, C.; Chew, Y.T.; Peng, Y. A momentum exchange-based immersed boundary-lattice Boltzmann method for simulating incompressible viscous flows. Phys. Lett. A 2006, 354, 173–182. [Google Scholar] [CrossRef]
- Saxena, A.; Kroll-Rabotin, J.-S.; Sanders, R.S. A numerical approach to model aggregate restructuring in shear flow using DEM in lattice-Boltzmann simulations. In Proceedings of the 12th International Conference on Computational Fluid Dynamics in the Oil & Gas, Metallurgical and Process Industries, Trondheim, Norway, 30 May–1 June 2017; pp. 761–772, ISBN 978-82-536-1544-8. [Google Scholar]
- Smoluchowski, M. Drei Vorträge über Diffusion, Brownsche Molekularbewegung und Koagulation von Kolloidteilchen. Z. Phys. 1916, 17, 557–585. [Google Scholar]
- Frungieri, G.; Vanni, M. Dynamics of a Shear-Induced Aggregation Process by a Combined Monte Carlo-Stokesian Dynamics approach. In Proceedings of the 9th International Conference on Multiphase Flow, Florence, Italy, 22–27 May 2016. [Google Scholar]
- Frungieri, G.; Vanni, M. Shear-induced aggregation of colloidal particles: A comparison between two different approaches to the modelling of colloidal interactions. Can. J. Chem. Eng. 2017, 95, 1768–1780. [Google Scholar] [CrossRef] [Green Version]
- Saffman, P.G.; Turner, J.S. On the collision of drops in turbulent clouds. J. Fluid Mech. 1956, 1, 16–30. [Google Scholar] [CrossRef]
- Becker, V.; Briesen, H. Tangential-force model for interactions between bonded colloidal particles. Phys. Rev. E 2008, 78, 061404. [Google Scholar] [CrossRef] [PubMed]
- Peglow, M.; Kumar, J.; Warnecke, G.; Heinrich, S.; Morl, L. A new technique to determine rate constants for growth and agglomeration with size- and time-dependent nuclei formation. Chem. Eng. Sci. 2006, 61, 282–292. [Google Scholar] [CrossRef]
- Ramkrishna, D. Population Balances: Theory and Applications to Particulate Systems in Engineering; Academic Press: Cambridge, MA, USA, 2000; ISBN 9780125769709. [Google Scholar]
- Toro, E.F. Riemann Solver and Numerical Methods for Fluid Dynamics: A Pratical Introduction; Springer: Berlin, Germany, 1999; ISBN 10: 3540659668/ISBN 13: 9783540659662. [Google Scholar]
- Kostoglou, M.; Karapantsios, T.D.; Matis, K.A. Modeling local flotation frequency in a turbulent flow field. Adv. Colloid Interface Sci. 2006, 122, 79–91. [Google Scholar] [CrossRef] [PubMed]
- Mirgaux, O.; Ablitzer, D.; Waz, E.; Bellot, J.P. Mathematical modelling and computer simulation of molten aluminium purification by flotation in stirred reactor. Metall. Mater. Trans. B 2009, 40, 363–375. [Google Scholar] [CrossRef]
- Wood, N.B. A simple method for the calculation of turbulent deposition to smooth and rough surfaces. J. Aerosol Sci. 1981, 12, 275–290. [Google Scholar] [CrossRef]
- Dupuy, M.; Xayasenh, A.; Waz, E.; Duval, H. Analysis of non-Brownian particle deposition from turbulent liquid-flow. AIChE J. 2015, 62, 891–904. [Google Scholar] [CrossRef]
- Lou, W.; Zhu, M. Numerical Simulations of Inclusion Behavior in Gas-Stirred Ladles. Metall. Mater. Trans. B 2013, 44, 762–782. [Google Scholar] [CrossRef]
- Higashitani, K.Y.; Kiyoyuki, K.; Matsuno, Y.; Hosokawe, G. Turbulent coagulation of particles dispersed in a viscous fluid. J. Chem. Eng. Jpn. 1983, 16, 299–304. [Google Scholar] [CrossRef]
- Ren, Z.; Harshe, Y.M.; Lattuada, M. Influence of the Potential Well on the Breakage Rate of Colloidal Aggregates in Simple Shear and Uniaxial Extensional Flows. Langmuir 2015, 31, 5712–5721. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L. Transport Phenomena and CFD Application during Process Metallurgy. In Advanced Processing of Metals and Materials (Sohn International Symposium), Volume 4, New, Improved and Existing Technologies: Non-ferrous Materials Extraction and Processing; Wiley: Hoboken, NJ, USA, 2006; Volume 2. [Google Scholar]
- Xie, Y.K.; Oesters, F. Experimental studies on the flow velocity of molten metals in a ladle model at centric gas blowing. Steel Res. 1992, 63, 93–104. [Google Scholar] [CrossRef]
- Ling, H.; Li, F.; Zhang, L.; Conejo, A.N. Investigation on the Effect of Nozzle Number on the Recirculation Rate and Mixing Time in the RH Process Using VOF plus DPM Model. Metall. Mater. Trans. B 2016, 47, 1950–1961. [Google Scholar] [CrossRef]
- Aoki, J.; Zhang, L.; Thomas, B.G. Modeling of Inclusion Removal in Ladle Refining. In Proceedings of the 3rd International Congress on Science & Technology of Steelmaking, Charlotte, NC, USA, 9–11 May 2005; AIST: Warrendale, PA, USA; pp. 319–332. [Google Scholar] [CrossRef]
- Warzecha, M.; Jowsa, J.; Warzecha, P.; Pfeifer, H. Numerical and Experimental Investigations of Steel Mixing Time in a 130-t Ladle. Steel Res. Int. 2008, 79, 852–860. [Google Scholar] [CrossRef]







| Collision Efficiency | |||||
|---|---|---|---|---|---|
| 0.028 | 0.071 | 0.213 | 0.319 | ||
| dp,1/dp,2 | 1 | ||||
| 2 | |||||
| 3 | |||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bellot, J.-P.; Kroll-Rabotin, J.-S.; Gisselbrecht, M.; Joishi, M.; Saxena, A.; Sanders, S.; Jardy, A. Toward Better Control of Inclusion Cleanliness in a Gas Stirred Ladle Using Multiscale Numerical Modeling. Materials 2018, 11, 1179. https://0-doi-org.brum.beds.ac.uk/10.3390/ma11071179
Bellot J-P, Kroll-Rabotin J-S, Gisselbrecht M, Joishi M, Saxena A, Sanders S, Jardy A. Toward Better Control of Inclusion Cleanliness in a Gas Stirred Ladle Using Multiscale Numerical Modeling. Materials. 2018; 11(7):1179. https://0-doi-org.brum.beds.ac.uk/10.3390/ma11071179
Chicago/Turabian StyleBellot, Jean-Pierre, Jean-Sebastien Kroll-Rabotin, Matthieu Gisselbrecht, Manoj Joishi, Akash Saxena, Sean Sanders, and Alain Jardy. 2018. "Toward Better Control of Inclusion Cleanliness in a Gas Stirred Ladle Using Multiscale Numerical Modeling" Materials 11, no. 7: 1179. https://0-doi-org.brum.beds.ac.uk/10.3390/ma11071179