Self-Healing Performance Assessment of Bacterial-Based Concrete Using Machine Learning Approaches
Abstract
:1. Introduction
1.1. Types of BSHC
1.1.1. Ureolytic Bacterial Healing Concrete (UBHC)
1.1.2. Aerobic Bacterial Healing Concrete (ABHC)
1.1.3. Nitrifying Bacterial Healing Concrete (NBHC)
1.2. Types of Bacteria
1.3. Influencing Factors of HP
1.4. Healing Performance Determination
2. Materials and Methods
2.1. Data Preparation
2.2. Machine Learning Algorithms
2.3. Prediction Ability Evaluation
2.4. Data Splitting
3. Results
Prediction Ability of ML Models
4. Discussion
4.1. K-Fold Cross Validation
4.2. Sensitivity Analysis
5. Conclusions
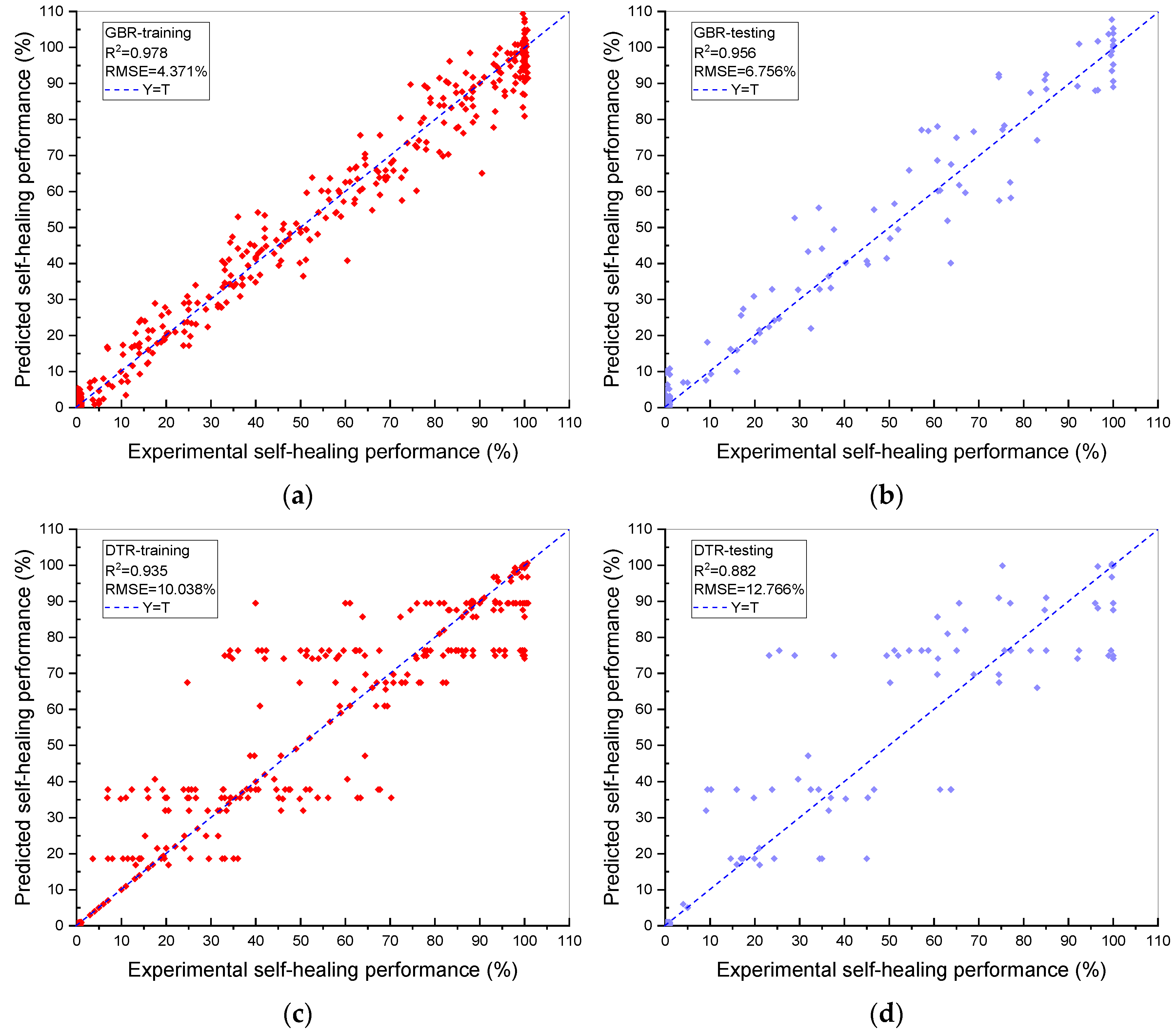
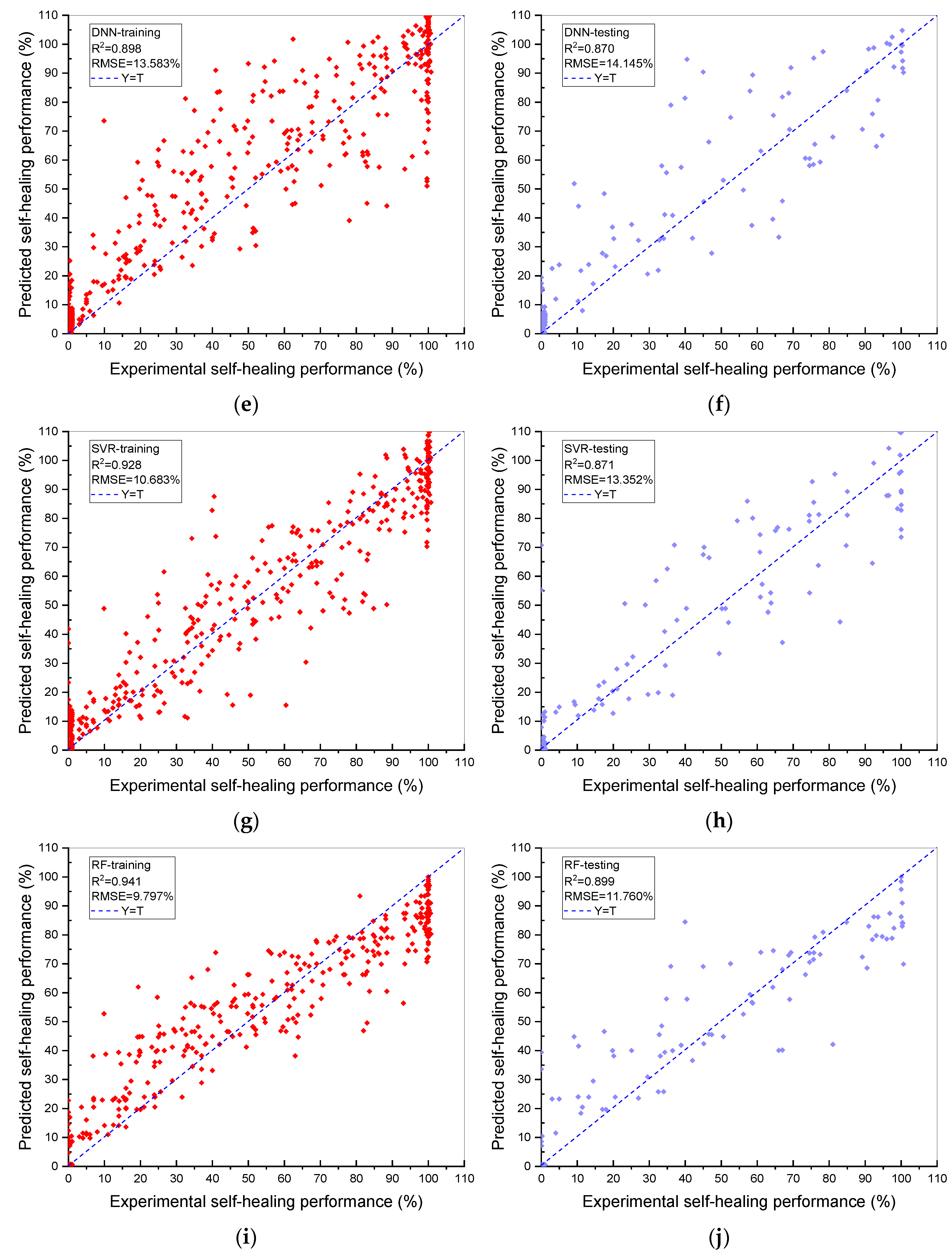
- The and RMSE values of the GBR model were 0.956 and 6.756%, respectively, which means that the prediction performance is excellent, and the prediction deviation is relatively low and reasonable. The GBR model was also compared to other ML algorithms, such as DTR, SVR, DNN and RF, and it showed an outstanding superiority to these ML models. Thus, it can be concluded that GBR is the optimal ML model that can accurately predict the HP of BSHC with the 22 variables.
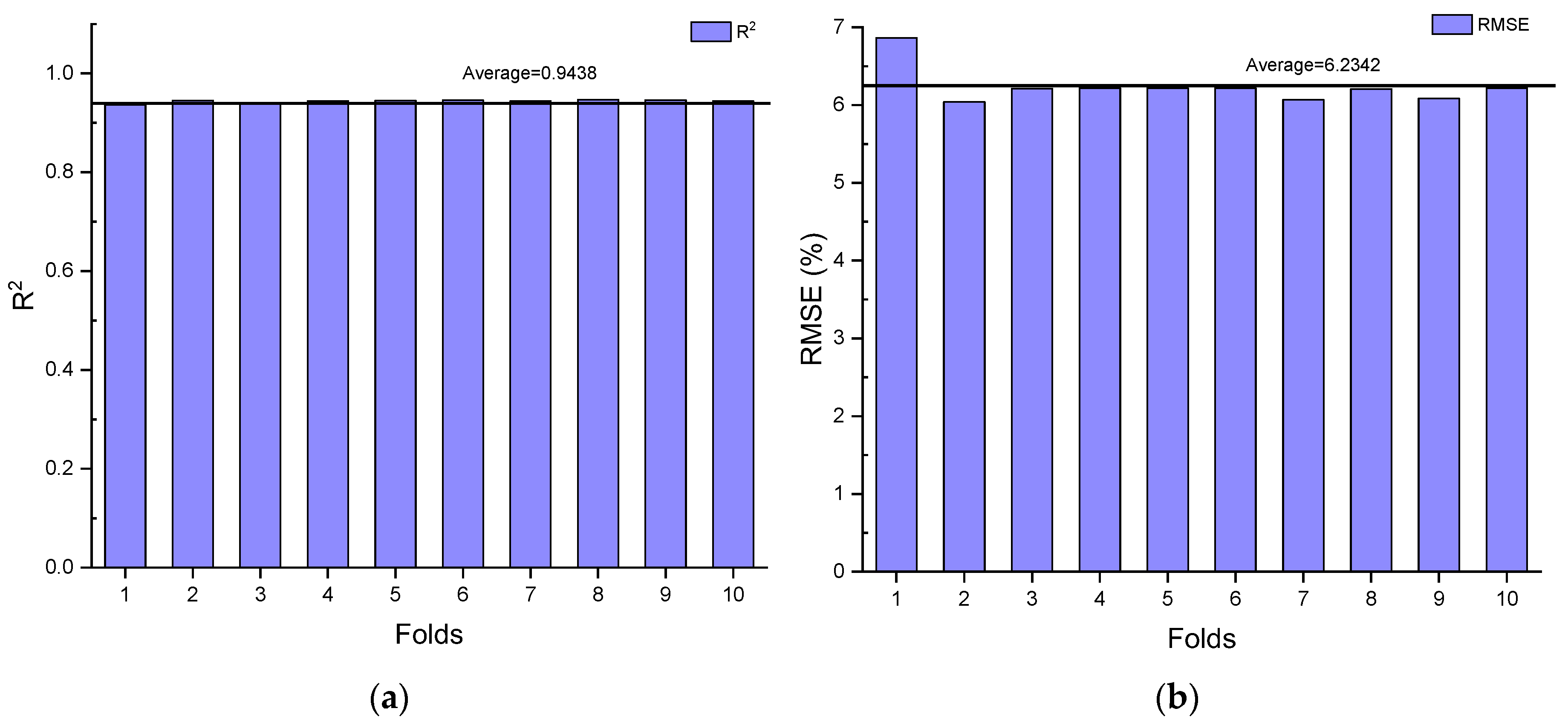
- Concerning the results of the 10-fold cross validation, the average R2 and RMSE values were 0.9438 and 6.2342%, respectively. Thus, it can be concluded that the robust prediction ability of the GBR model is convincing.
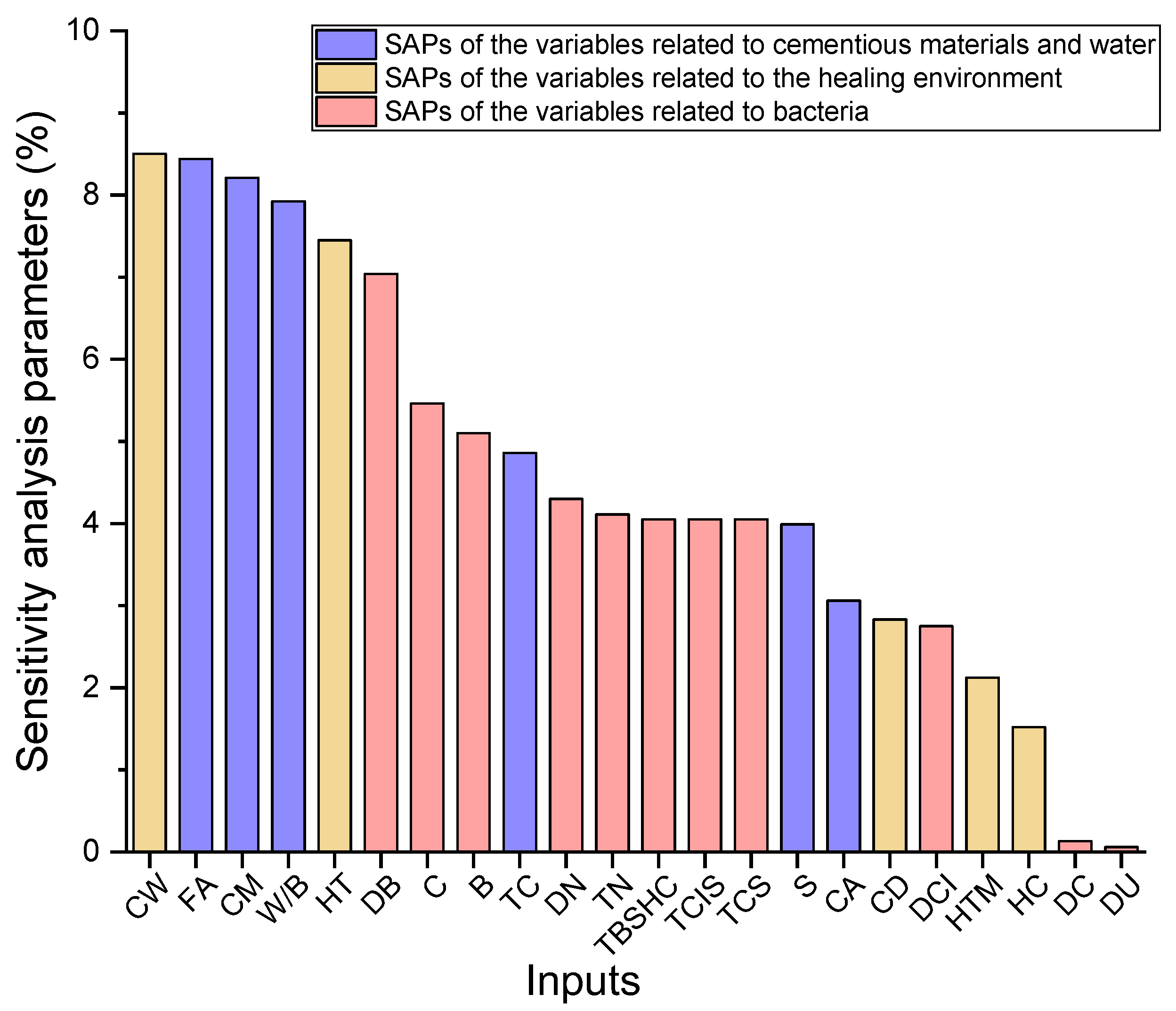
- All variables in the GBR model were studied to inspect the influence on the HP of BSHC. It was observed that CW, FA, CM, W/B, HT and DB are key variables and have relatively higher effects on the HP of BHSC, which means that they cannot be neglected during the ML-aided self-healing concrete design.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Number | Representation |
|---|---|
| 0 | No carrier |
| 1 | Expanded clay |
| 2 | Expanded perlite |
| 3 | Graphene nanoplatelets |
| 4 | Coir |
| 5 | Flax |
| 6 | Jute |
| 7 | Low alkali calcium sulphoaluminate |
| 8 | Recycled brick aggregate |
| Number | Representation |
|---|---|
| 0 | No bacteria |
| 1 | Bacillus subtilis |
| 2 | Bacillus cohnii |
| 3 | Bacillus alkalinitrilicus |
| 4 | Bacillus pasteurii |
| 5 | Bacillus sphaericus |
| 6 | Bacillus megaterium |
| Number | Representation |
|---|---|
| 1 | Ambient water condition |
| 2 | Ambient air condition |
| 3 | Wet–dry cycles |
| Number | Representation |
|---|---|
| 0 | Autogenous healing |
| 1 | ABHC |
| 2 | UBHC |
| Number | Representation |
|---|---|
| 1 | Peptone |
| 2 | Yeast |
| 3 | Beef extract |
| Number | Representation |
|---|---|
| 0 | Water |
| 1 | Air |
| 2 | Calcium lactate |
| Number | Representation |
|---|---|
| 1 | CEM I 42.5N |
| 2 | CEM II 42.5N |
| 3 | CEM I 52.5N |
| Number | Representation |
|---|---|
| 1 | Calcium nitrate |
| 2 | Calcium lactate |
| 3 | Ca(OH)2 |
| Number | Representation |
|---|---|
| 1 | Cracking width measurement |
| 2 | Cracking area measurement |
| 3 | Ultrasound pulse velocity measurement |
| 4 | Regained strength measurement |
| 5 | Anti-seepage repairing measurement |
References
- Habeeb, G.A.; Fayyadh, M.M. Rice Husk Ash Concrete: The Effect of RHA Average Particle Size on Mechanical Properties and Drying Shrinkage. Aust. J. Basic Appl. Sci. 2009, 3, 1616–1622. [Google Scholar]
- HM, J. Bacteria-Based Self-Healing Concrete: Towards Standardisation. Res. Dev. Mater. Sci. 2019, 10, 3–5. [Google Scholar] [CrossRef]
- Jensen, M.M.; Johannesson, B.; Geiker, M. A coupled chemical and mass transport model for concrete durability. Civil-Comp Proc. 2012, 100, 1–18. [Google Scholar] [CrossRef]
- Klee, H.; Coles, E. The cement sustainability initiative: Implementing change across a global industry. Corp. Environ. Strateg. 2004, 11, 21–28. [Google Scholar] [CrossRef]
- Cailleux, E.; Pollet, V. Investigations on the development of self-healing properties in protective coatings for concrete and repair mortars. In Proceedings of the 2nd International Conference on Self-Healing Materials, Chicago, IL, USA, 28 June 2009; Volume 32, pp. 1–4. [Google Scholar]
- Huang, X.; Ge, J.; Kaewunruen, S.; Su, Q. The self-sealing capacity of environmentally friendly, highly damped, fibre-reinforced concrete. Materials 2020, 13, 298. [Google Scholar] [CrossRef] [Green Version]
- Tittelboom, K.V.; Belie, N. De Self-Healing in Cementitious Materials—A Review. Materials 2013, 6, 2182–2217. [Google Scholar] [CrossRef] [Green Version]
- De Belie, N.; Gruyaert, E.; Al-Tabbaa, A.; Antonaci, P.; Baera, C.; Bajare, D.; Darquennes, A.; Davies, R.; Ferrara, L.; Jefferson, T.; et al. A Review of Self-Healing Concrete for Damage Management of Structures. Adv. Mater. Interfaces 2018, 5, 1–28. [Google Scholar] [CrossRef]
- Zhuang, X.; Zhou, S. The prediction of self-healing capacity of bacteria-based concrete using machine learning approaches. Comput. Mater. Contin. 2019, 59, 57–77. [Google Scholar] [CrossRef] [Green Version]
- Suleiman, A.R.; Nehdi, M.L. Modeling self-healing of concrete using hybrid genetic algorithm-artificial neural network. Materials 2017, 10, 135. [Google Scholar] [CrossRef]
- Li, W.; Dong, B.; Yang, Z.; Xu, J.; Chen, Q.; Li, H.; Xing, F.; Jiang, Z. Recent Advances in Intrinsic Self-Healing Cementitious Materials. Adv. Mater. 2018, 30, 1705679. [Google Scholar] [CrossRef]
- Tziviloglou, E.; Wiktor, V.; Jonkers, H.M.; Schlangen, E. Selection of nutrient used in biogenic healing agent for cementitious materials. Front. Mater. 2017, 4, 1–7. [Google Scholar] [CrossRef]
- Jonkers, H.M.; Thijssen, A.; Muyzer, G.; Copuroglu, O.; Schlangen, E. Application of bacteria as self-healing agent for the development of sustainable concrete. Ecol. Eng. 2010, 36, 230–235. [Google Scholar] [CrossRef]
- Zhu, Y.; Wu, M.; Gao, N.; Chu, W.; An, N.; Wang, Q.; Wang, S. Removal of antimonate from wastewater by dissimilatory bacterial reduction: Role of the coexisting sulfate. J. Hazard. Mater. 2018, 341, 36–45. [Google Scholar] [CrossRef] [PubMed]
- Erşan, Y.Ç.; Verbruggen, H.; De Graeve, I.; Verstraete, W.; De Belie, N.; Boon, N. Nitrate reducing CaCO3 precipitating bacteria survive in mortar and inhibit steel corrosion. Cem. Concr. Res. 2016, 83, 19–30. [Google Scholar] [CrossRef]
- Erşan, Y.Ç.; Da Silva, F.B.; Boon, N.; Verstraete, W.; De Belie, N. Screening of bacteria and concrete compatible protection materials. Constr. Build. Mater. 2015, 88, 196–203. [Google Scholar] [CrossRef]
- Andrew, T.C.S.; Syahrizal, I.I.; Jamaluddin, M.Y. Effective Microorganisms for Concrete (EMC) Admixture—Its Effects to the Mechanical Properties of Concrete. Casp. J. Appl. Sci. Res. 2012, 419–426. [Google Scholar]
- Wiktor, V.; Jonkers, H.M. Quantification of crack-healing in novel bacteria-based self-healing concrete. Cem. Concr. Compos. 2011, 33, 763–770. [Google Scholar] [CrossRef]
- Ferrara, L.; Krelani, V.; Carsana, M. A “fracture testing” based approach to assess crack healing of concrete with and without crystalline admixtures. Constr. Build. Mater. 2014, 68, 535–551. [Google Scholar] [CrossRef]
- Reinhardt, H.W.; Jooss, M. Permeability and self-healing of cracked concrete as a function of temperature and crack width. Cem. Concr. Res. 2003, 33, 981–985. [Google Scholar] [CrossRef]
- Maes, M.; Snoeck, D.; De Belie, N. Chloride penetration in cracked mortar and the influence of autogenous crack healing. Constr. Build. Mater. 2016, 115, 114–124. [Google Scholar] [CrossRef]
- Muhammad, N.Z.; Shafaghat, A.; Keyvanfar, A.; Majid, M.Z.A.; Ghoshal, S.K.; Mohammadyan Yasouj, S.E.; Ganiyu, A.A.; Samadi Kouchaksaraei, M.; Kamyab, H.; Taheri, M.M.; et al. Tests and methods of evaluating the self-healing efficiency of concrete: A review. Constr. Build. Mater. 2016, 112, 1123–1132. [Google Scholar] [CrossRef]
- Luo, M.; Qian, C.X.; Li, R.Y. Factors affecting crack repairing capacity of bacteria-based self-healing concrete. Constr. Build. Mater. 2015, 87, 1–7. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, C.; Zhou, A.; Yang, C.; Zhao, L.; Li, Z. Aragonite formation induced by open cultures of microbial consortia to heal cracks in concrete: Insights into healing mechanisms and crystal polymorphs. Constr. Build. Mater. 2019, 224, 815–822. [Google Scholar] [CrossRef]
- Khaliq, W.; Ehsan, M.B. Crack healing in concrete using various bio influenced self-healing techniques. Constr. Build. Mater. 2016, 102, 349–357. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, Y.; Feng, T.; Zhou, M.; Zhao, L.; Zhou, A.; Li, Z. Immobilising bacteria in expanded perlite for the crack self-healing in concrete. Constr. Build. Mater. 2017, 148, 610–617. [Google Scholar] [CrossRef]
- Jiang, L.; Jia, G.; Jiang, C.; Li, Z. Sugar-coated expanded perlite as a bacterial carrier for crack-healing concrete applications. Constr. Build. Mater. 2020, 232, 117222. [Google Scholar] [CrossRef]
- Jiang, L.; Jia, G.; Wang, Y.; Li, Z. Optimization of Sporulation and Germination Conditions of Functional Bacteria for Concrete Crack-Healing and Evaluation of their Repair Capacity. ACS Appl. Mater. Interfaces 2020, 12, 10938–10948. [Google Scholar] [CrossRef]
- Liu, C.; Xu, X.; Lv, Z.; Xing, L. Self-healing of concrete cracks by immobilising microorganisms in recycled aggregate. J. Adv. Concr. Technol. 2020, 18, 168–178. [Google Scholar] [CrossRef] [Green Version]
- Saleem, B.; Hussain, A.; Khattak, A.; Khan, A. Performance evaluation of bacterial self-healing rigid pavement by incorporating recycled brick aggregate. Cem. Concr. Compos. 2021, 117, 103914. [Google Scholar] [CrossRef]
- Metwally, G.A.M.; Mahdy, M.; El-Raheem, A.H.A. Performance of bio concrete by using bacillus pasteurii bacteria. Civ. Eng. J. 2020, 6, 1443–1456. [Google Scholar] [CrossRef]
- Su, Y.; Zheng, T.; Qian, C. Application potential of Bacillus megaterium encapsulated by low alkaline sulphoaluminate cement in self-healing concrete. Constr. Build. Mater. 2021, 273, 121740. [Google Scholar] [CrossRef]
- Rauf, M.; Khaliq, W.; Khushnood, R.A.; Ahmed, I. Comparative performance of different bacteria immobilised in natural fibers for self-healing in concrete. Constr. Build. Mater. 2020, 258, 119578. [Google Scholar] [CrossRef]
- Mondal, S.; Ghosh, A.D. Investigation into the optimal bacterial concentration for compressive strength enhancement of microbial concrete. Constr. Build. Mater. 2018, 183, 202–214. [Google Scholar] [CrossRef]
- Grabiec, A.M.; Klama, J.; Zawal, D.; Krupa, D. Modification of recycled concrete aggregate by calcium carbonate biodepo sition. Constr. Build. Mater. 2012, 34, 145–150. [Google Scholar] [CrossRef]
- Naderpour, H.; Hossein, A.; Fakharian, P. Compressive strength prediction of environmentally friendly concrete using arti fi cial neural networks. J. Build. Eng. 2018, 16, 213–219. [Google Scholar] [CrossRef]
- Atici, U. Prediction of the strength of mineral admixture concrete using multivariable regression analysis and an artificial neural network. Expert Syst. Appl. 2011, 38, 9609–9618. [Google Scholar] [CrossRef]
- Duan, Z.H.; Kou, S.C.; Poon, C.S. Using artificial neural networks for predicting the elastic modulus of recycled aggregate concrete. Constr. Build. Mater. 2013, 44, 524–532. [Google Scholar] [CrossRef]
- Kaloop, M.R.; Kumar, D.; Samui, P.; Hu, J.W.; Kim, D. Compressive strength prediction of high-performance concrete using gradient tree boosting machine. Constr. Build. Mater. 2020, 264, 120198. [Google Scholar] [CrossRef]
- Yoon, J.Y.; Kim, H.; Lee, Y.J.; Sim, S.H. Prediction model for mechanical properties of lightweight aggregate concrete using artificial neural network. Materials 2019, 12, 2678. [Google Scholar] [CrossRef] [Green Version]
- Safavian, S.R.; Landgrebe, D. A Survey of Decision Tree Classifier Methodology. IEEE Trans. Syst. Man Cybern. 1991, 21, 660–674. [Google Scholar] [CrossRef] [Green Version]
- Topçu, I.B.; Saridemir, M. Prediction of mechanical properties of recycled aggregate concretes containing silica fume using artificial neural networks and fuzzy logic. Comput. Mater. Sci. 2008, 42, 74–82. [Google Scholar] [CrossRef]
- Raghavendra, S.; Deka, P.C. Support vector machine applications in the field of hydrology: A review. Appl. Soft Comput. J. 2014, 19, 372–386. [Google Scholar] [CrossRef]
- DeRousseau, M.A.; Kasprzyk, J.R.; Srubar, W.V. Computational design optimisation of concrete mixtures: A review. Cem. Concr. Res. 2018, 109, 42–53. [Google Scholar] [CrossRef]
- Zheng, Y. Trajectory data mining: An overview. ACM Trans. Intell. Syst. Technol. 2015, 6, 1–41. [Google Scholar] [CrossRef]
- Kisi, O. Pan evaporation modeling using least square support vector machine, multivariate adaptive regression splines and M5 model tree. J. Hydrol. 2015, 528, 312–320. [Google Scholar] [CrossRef]
- Kam, T.H. Random Decision Forests Tin Kam Ho Perceptron training. Proc. 3rd Int. Conf. Doc. Anal. Recognit. 1995, 1, 278–282. [Google Scholar]
- Zhang, M.L.; Zhou, Z.H. ML-KNN: A lazy learning approach to multi-label learning. Pattern Recognit. 2007, 40, 2038–2048. [Google Scholar] [CrossRef] [Green Version]
- Tamura, S.; Tateishi, M. Capabilities of a four-layered feedforward neural network: Four layers versus three. IEEE Trans. Neural Netw. 1997, 8, 251–255. [Google Scholar] [CrossRef]
- Li, J.Y.; Chow, T.W.S.; Yu, Y.L. Estimation theory and optimisation algorithm for the number of hidden units in the higher-order feedforward neural network. IEEE Int. Conf. Neural Netw. Conf. Proc. 1995, 3, 1229–1233. [Google Scholar] [CrossRef]
- Sheela, K.G.; Deepa, S.N. Selection of number of hidden neurons in neural networks in renewable energy systems. J. Sci. Ind. Res. 2014, 73, 686–688. [Google Scholar]
- Syarif, I.; Prugel-Bennett, A.; Wills, G. SVM parameter optimisation using grid search and genetic algorithm to improve classification performance. Telkomnika Telecommun. Comput. Electron. Control. 2016, 14, 1502–1509. [Google Scholar] [CrossRef]
- Xiao, T.; Ren, D.; Lei, S.; Zhang, J.; Liu, X. Based on grid-search and PSO parameter optimisation for Support Vector Machine. In Proceeding of the 11th World Congress on Intelligent Control and Automation, Shenyang, China, 29 June–4 July 2014; Volume 2015, pp. 1529–1533. [Google Scholar] [CrossRef]
- Huang, C.L.; Dun, J.F. A distributed PSO-SVM hybrid system with feature selection and parameter optimisation. Appl. Soft Comput. J. 2008, 8, 1381–1391. [Google Scholar] [CrossRef]
- Gholami, R.; Shahraki, A.R.; Jamali Paghaleh, M. Prediction of hydrocarbon reservoirs permeability using support vector machine. Math. Probl. Eng. 2012, 2012, 670723. [Google Scholar] [CrossRef] [Green Version]
- Li, X.Z.; Kong, J.M. Application of GA-SVM method with parameter optimisation for landslide development prediction. Nat. Hazards Earth Syst. Sci. 2014, 14, 525–533. [Google Scholar] [CrossRef] [Green Version]
- Bilim, C.; Atiş, C.D.; Tanyildizi, H.; Karahan, O. Predicting the compressive strength of ground granulated blast furnace slag concrete using artificial neural network. Adv. Eng. Softw. 2009, 40, 334–340. [Google Scholar] [CrossRef]
- Feng, D.C.; Liu, Z.T.; Wang, X.D.; Chen, Y.; Chang, J.Q.; Wei, D.F.; Jiang, Z.M. Machine learning-based compressive strength prediction for concrete: An adaptive boosting approach. Constr. Build. Mater. 2020, 230, 117000. [Google Scholar] [CrossRef]
- Song, H.; Ahmad, A.; Farooq, F.; Ostrowski, K.A.; Maślak, M.; Czarnecki, S.; Aslam, F. Predicting the compressive strength of concrete with fly ash admixture using machine learning algorithms. Constr. Build. Mater. 2020, 308, 125021. [Google Scholar] [CrossRef]
- Kaewunruen, S.; Sussman, J.M.; Matsumoto, A. Grand challenges in transportation and transit systems. Front. Built Environ. 2016, 2, 1–5. [Google Scholar] [CrossRef] [Green Version]

| Types of Variables | Symbol | Unit | Minimum | Maximum |
|---|---|---|---|---|
| Inputs | C | - | 0 | 8 |
| TC | - | 1 | 3 | |
| B | - | 0 | 6 | |
| DB | cells/g | 0 | 2.6 × 109 | |
| TBSHC | - | 0 | 2 | |
| TCIS | - | 1 | 3 | |
| DCI | g/g | 0 | 0.034 | |
| TCS | - | 0 | 2 | |
| DC | g/g | 0 | 0.034 | |
| TN | - | 1 | 3 | |
| DN | g/L | 0 | 4 | |
| DU | g/L | 0 | 0.024 | |
| FA | g/g | 0.204 | 0.666 | |
| CA | g/g | 0 | 0.522 | |
| CM | g/g | 0.156 | 0.222 | |
| W/B | - | 0.4 | 0.599 | |
| S | g/g | 0 | 1.564 | |
| CD | days | 3 | 56 | |
| CW | mm | 0.027 | 1.152 | |
| HC | - | 1 | 3 | |
| HT | days | 3 | 100 | |
| HTM | - | 1 | 5 | |
| Output | HP | % | 0 | 100.76 |
| Algorithm | Dataset | HP Prediction Ability | |
|---|---|---|---|
| R2 | RMSE (%) | ||
| GBR | Training | 0.978 | 4.371 |
| Testing | 0.956 | 6.756 | |
| DTR | Training | 0.935 | 10.038 |
| Testing | 0.882 | 12.766 | |
| DNN | Training | 0.898 | 13.583 |
| Testing | 0.870 | 14.145 | |
| SVR | Training | 0.928 | 10.683 |
| Testing | 0.871 | 13.352 | |
| RF | Training | 0.941 | 9.797 |
| Testing | 0.899 | 11.760 | |
| Algorithms | Parameters | Setting |
|---|---|---|
| DNN | Hidden layers | 4 |
| Hidden neurons | 30-30-30-30 | |
| Learning rate | 0.0010 | |
| Activation function | Maxout | |
| GBR | Depthmax | 21 |
| Splitmin | 0.001 | |
| Learning rate | 0.9001 | |
| Number of trees | 21 | |
| DTR | Depthmax | 10 |
| Splitmin | 1.000 | |
| Leafmin | 1 | |
| Gainmin | 0.0010 | |
| SVR | Cpenalty | 1 |
| Epsilon | 0.001 | |
| Gamma | 5000 | |
| Kernel type | Radial | |
| RF | Depthmax | 60 |
| Splitmin | 100.000 | |
| Leafmin | 60 | |
| Gainmin | 0.3007 | |
| Number of trees | 11 |
| Folds | HP Prediction Ability | |
|---|---|---|
| R2 | RMSE (%) | |
| Fold 1 | 0.937 | 6.864 |
| Fold 2 | 0.945 | 6.039 |
| Fold 3 | 0.940 | 6.210 |
| Fold 4 | 0.944 | 6.218 |
| Fold 5 | 0.945 | 6.218 |
| Fold 6 | 0.946 | 6.218 |
| Fold 7 | 0.944 | 6.067 |
| Fold 8 | 0.947 | 6.206 |
| Fold 9 | 0.946 | 6.084 |
| Fold 10 | 0.944 | 6.218 |
| Average | 0.9438 | 6.2342 |
| SD | 0.0029 | 0.2208 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Sresakoolchai, J.; Qin, X.; Ho, Y.F.; Kaewunruen, S. Self-Healing Performance Assessment of Bacterial-Based Concrete Using Machine Learning Approaches. Materials 2022, 15, 4436. https://0-doi-org.brum.beds.ac.uk/10.3390/ma15134436
Huang X, Sresakoolchai J, Qin X, Ho YF, Kaewunruen S. Self-Healing Performance Assessment of Bacterial-Based Concrete Using Machine Learning Approaches. Materials. 2022; 15(13):4436. https://0-doi-org.brum.beds.ac.uk/10.3390/ma15134436
Chicago/Turabian StyleHuang, Xu, Jessada Sresakoolchai, Xia Qin, Yiu Fan Ho, and Sakdirat Kaewunruen. 2022. "Self-Healing Performance Assessment of Bacterial-Based Concrete Using Machine Learning Approaches" Materials 15, no. 13: 4436. https://0-doi-org.brum.beds.ac.uk/10.3390/ma15134436







