An Optimal and Stable Algorithm for Clustering Numerical Data
Abstract
:1. Introduction
2. Preliminaries
2.1. k-Means Clustering Framework
- Step 1—First, initialize the number of clusters, k.
- Step 2—Randomly select Z from X as the center of clusters (better known as centroids).
- Step 3—Assign X to the closest cluster centroid based on the distance of each X and Z. The distance is typically calculated using Euclidean distance as Equation (1).
- Step 5—Repeat Steps 3 and 4 and stop when the process intra- and inter-cluster dissimilarity objective function are minimized. The objective function is computed as in Equation (7)
| Algorithm 1 FUZZY C-MEANS (. |
|
Input: dataset X, number of clusters k, and weighting exponent Output: Set of clusters |
2.2. k-AMH Clustering Framework
2.2.1. k-AMH Algorithm for Categorical Clustering
- Step 1—First, initialize the number of clusters, k.
- Step 2—Randomly select H from X as the center of the clusters (better known as medoids).
- Step 4—Assign X to C when the final H is obtained.
| Algorithm 2 k-AMH (. |
|
Input: dataset X, number of clusters k, and weighting exponent Output: Set of clusters |
2.2.2. k-AMH Algorithm for Numerical Clustering
- Step 1—First, initialize the number of clusters, k.
- Step 2—Randomly select Z from X as the center of the clusters (better known as medoids).
- Step 3—Replace the medoids, Z, by testing each one until . The updates are complete when the objective function is minimized as Equation (22).
- Step 4—Assign X to C when the final Z is obtained.
| Algorithm 3 k-AMH NUMERIC (. |
|
Input: dataset X, number of clusters k, and weighting exponent Output: Set of clusters |
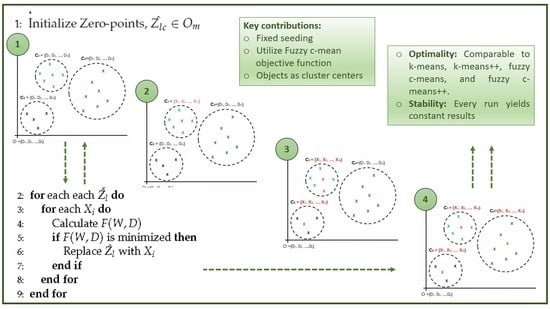
3. Proposed Clustering Algorithm with a Constant Seeding Selection
3.1. Proposed Seeding Selection Method
3.2. Proposed Algorithm
- Step 1—First, initialize the number of clusters, k.
- Step 2—Select as the center of the clusters (better known as medoids).
- Step 4—Assign X to C when the final is obtained.
3.3. Computational Complexity
| Algorithm 4 Zk-AMH(. |
|
Input: dataset X, number of clusters k, and weighting exponent Output: Set of clusters |
4. Experimental Setup
4.1. Dataset
4.2. Evaluation Method
5. Results
5.1. Cluster Optimality
5.2. Cluster Stability
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jain, A.K.; Dubes, R.C. Algorithm for Clustering Data; Prentice Hall Inc.: Hoboken, NJ, USA, 1988. [Google Scholar]
- Gan, G.; Ma, C.; Wu, J. Data Clustering: Theory, Algorithms, and Applications; Society for Industrial and Applied Mathematics: Philadelphia, VA, USA, 2007. [Google Scholar]
- Jain, A.K.; Murthy, M.N.; Flynnand, P.J. Data clustering: A review. ACM Comput. Surv. 1999, 31, 264–323. [Google Scholar] [CrossRef]
- Kaufman, L.; Rousseeuw, P.J. Finding Groups in Data: An Introduction to Cluster Analysis; Wiley and Sons: New York, NY, USA, 1990. [Google Scholar]
- Xu, R.; Wunsch, D. Clustering; John Wiley and Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Tan, T.; Steinbach, M.; Kumar, V. Introduction to Data Mining; Pearson Education, Inc.: Boston, MA, USA, 2006. [Google Scholar]
- Everitt, B.; Landau, S.; Leese, M. Cluster Analysis; Arnold: London, UK, 2001. [Google Scholar]
- Fielding, H. Cluster and Classification Techniques for Biosciences; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Han, J.; Kamber, M. Data Mining: Concepts and Techniques; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2001. [Google Scholar]
- MacQueen, J.B. Some methods for classification and analysis of multivariate observations. In 5th Berkeley Symposium on Mathematical Statistics and Probability; University of California Press: Berkeley, CA, USA, 1967; pp. 281–297. [Google Scholar]
- Bezdek, J.C. Pattern Recognition with Fuzzy Objective Function Algorithms; Plenum: New York, NY, USA, 1981. [Google Scholar]
- Huang, J.Z. Extensions to the k-means algorithm for clustering large data sets with categorical values. Data Min. Knowl. Discov. 1998, 2, 283–304. [Google Scholar] [CrossRef]
- Huang, J.Z.; Ng, M.K. A fuzzy k-modes algorithm for clustering categorical data. IEEE Trans. Fuzzy Syst. 1999, 7, 46–452. [Google Scholar]
- Caruso, G.; Gattone, S.A.; Balzanella, A.; Di Battista, T. Cluster Analysis: An Application to a Real Mixed-Type Data set. In Models and Theories in Social Systems. Studies in Systems, Decision and Control; Flaut, C., Hošková-Mayerová, Š., Flaut, D., Eds.; Springer: Cham, Switzerland, 2019; Volume 179, pp. 525–533. [Google Scholar]
- Alibuhtto, M.C.; Mahat, N.I. New approach for finding number of clusters usingdistance based k-means algorithm. Int. J. Eng. Sci. Math. 2019, 8, 111–122. [Google Scholar]
- Xie, H.; Zhang, L.; Lim, C.P.; Yu, Y.; Liu, C.; Liu, H.; Walters, J. Improving k-means clustering with enhanced firefly. Algorithms Appl. Soft Comput. 2019, 84, 105763. [Google Scholar] [CrossRef]
- Seman, A.; Bakar, Z.A.; Isa, M.N. An efficient clustering algorithm for partitioning y-short tandem repeats data. BMC Res. Notes 2012, 5, 1–13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Arthur, D.; Vassilvitskii, S. k-means++: The advantages of careful seeding. In Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms, New Orleans, LA, USA, 7–9 January 2007; pp. 1027–1035. [Google Scholar]
- Zou, K.; Wang, Z.; Pei, S.; Hu, M. An New Initialization Method for Fuzzy c-Means Algorithm Based on Density. In Fuzzy Information and Engineering. Advances in Soft Computing; Cao, B., Zhang, C., Li, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Stetco, A.; Zeng, X.-J.; Keane, J. Fuzzy c-means++: Fuzzy c-means with effective seeding initialization. Expert Syst. Appl. 2015, 42, 7541–7548. [Google Scholar] [CrossRef]
- Ronald, Y.; Filev, R.; Dimitar, P. Approximate clustering via the mountain method. IEEE Trans. Syst. Man Cybern. 1994, 24, 1279–1284. [Google Scholar]
- Chiu, S.L. Fuzzy model identification based on cluster estimation. J. Intell. Fuzzy Syst. 1994, 2, 267–278. [Google Scholar] [CrossRef]
- Pei, J.; Fan, J.; Xie, W. An initialization method of cluster centers. J. Electron. Sci. 1999, 21, 320–325. [Google Scholar] [CrossRef]
- Manochandar, S.; Punniyamoorthy, M.; Jeyachitra, R.K. Development of new seed with modified validity measures for k-means clustering. Comput. Ind. Eng. 2020, 141, 106290. [Google Scholar] [CrossRef]
- Zhang, X.; He, Y.; Jin, Y.; Qin, H.; Azhar, M.; Huang, J.Z. A robust k-means clustering algorithm based on observation point mechanism. Hindawi Complex. 2020, 2020, 3650926. [Google Scholar] [CrossRef]
- Fränti, P.; Sieranoja, S. How much can k-means be improved by using better initialization and repeats? Pattern Recognit. 2019, 93, 95–112. [Google Scholar] [CrossRef]
- Seman, A.; Sapawi, A.M. Extensions to the k-amh algorithm for numerical clustering. J. ICT 2018, 17, 587–599. [Google Scholar]
- Seman, A.; Sapawi, A.M.; Salleh, M.Z. Towards development of clustering applications for large-scale comparative genotyping and kinship analysis using y-short tandem repeats. OMICS 2015, 19, 361–367. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Seman, A.; Sapawi, A.M. Complementary Optimization Procedure for Final Cluster Analysis of Clustering Categorical Data. In Advances in Intelligent Systems and Computing; Vasant, P., Zelinka, I., Weber, G.W., Eds.; Springer: Cham, Switzerland, 2020; pp. 301–310. [Google Scholar]
- Von Luxburg, U. Clustering stability: An overview. Found. Trends Mach. Learn. 2010, 2, 235–274. [Google Scholar]
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Merz, J.; Murphy, P.M. UCI Machine Learning Repository; School of Information and Computer Science, University of California: Irvine, CA, USA, 1996. [Google Scholar]
- Fowlkes, E.B.; Mallows, C.L. A method for comparing two hierarchical clusterings. J. Am. Stat. Assoc. 1983, 78, 553–569. [Google Scholar] [CrossRef]




| Dataset | Description | Number of | ||
|---|---|---|---|---|
| Objects | Classes | Attributes | ||
| 1. Iris | The Iris dataset is used to analyze the three types of Iris plants. | 150 | 3 | 4 |
| 2. Haberman | Haberman’s survival dataset is used for breast cancer studies. | 306 | 2 | 3 |
| 3. Pima | The Pima Indians Diabetes Dataset was provided by the National Institute of Diabetes and Digestive and Kidney Diseases. | 393 | 3 | 8 |
| 4. Wine | The Wine dataset is used for chemical analysis of wines grown in a specific region of Italy. | 178 | 3 | 13 |
| 5. Seed | The Seed dataset is used to compare three different varieties of wheat: Kama, Rosa, and Canadian. | 210 | 3 | 7 |
| 6. User knowledge | The User knowledge dataset is employed to study the knowledge status of students about electrical Direct Current (DC) machines. The dataset was the combination of a 258-item training set and 145 item test set. | 403 | 4 | 5 |
| 7. E-coli | The E-coli dataset is used to predict protein localization sites. | 336 | 8 | 7 |
| 8. Cleveland | The Cleveland dataset is used to diagnose coronary artery disease. The dataset contained 303 items with 75 attributes and was divided into 5 classes. However, the dataset was filtered down to 297 items with only 5 numerical attributes. | 297 | 5 | 5 |
| Algorithm | Seeding Method | Cluster Approach | Cluster Center |
|---|---|---|---|
| 1. k-means [10] | Random | Hard | Mean |
| 2. k-means++ [18] | Probability | Hard | Mean |
| 3. Fuzzy c-means [11] | Random | Soft | Mean |
| 4. Fuzzy c-means++ [20] | Probability | Soft | Mean |
| 5. k-AMH Numeric [27] | Random | Soft | Object |
| 6. k-AMH Numeric++ | |||
| (Using k-means++ seeding) | Probability | Soft | Object |
| 7. Zk-AMH | |||
| (The proposed algorithm) | Zero-Seeding | Soft | Object |
| FM Index—Games–Howell | ||||||
|---|---|---|---|---|---|---|
| (I) Algo. | (J) Algo. | Mean Diff. (I-J) | Std. Err. | p-Value | 95% CI | |
| Lower Bound | Upper Bound | |||||
| Zk-AMH | k-means | 0.12 | 0.01 | <0.01 | 0.09 | 0.14 |
| k-means++ | 0.11 | 0.01 | <0.01 | 0.08 | 0.14 | |
| Fuzzy c-means | 0.01 | 0.01 | 0.98 | −0.02 | 0.04 | |
| Fuzzy c-means++ | 0.07 | 0.01 | <0.01 | −0.04 | 0.10 | |
| k-AMH numeric | 0.01 | 0.01 | 0.98 | −0.02 | 0.04 | |
| k-AMH numeric++ | 0.01 | 0.01 | 0.81 | −0.02 | 0.05 | |
| FMI Score | Algorithm | Dataset | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| Mean | k-means | 0.641 | 0.507 | 0.563 | 0.540 | 0.660 | 0.522 | 0.311 | 0.247 |
| k-means++ | 0.694 | 0.514 | 0.597 | 0.569 | 0.699 | 0.414 | 0.312 | 0.248 | |
| Fuzzy c-means | 0.891 | 0.502 | 0.633 | 0.701 | 0.898 | 0.509 | 0.455 | 0.266 | |
| Fuzzy c-means++ | 0.823 | 0.516 | 0.602 | 0.589 | 0.757 | 0.407 | 0.447 | 0.251 | |
| k-AMH numeric | 0.901 | 0.488 | 0.661 | 0.713 | 0.885 | 0.446 | 0.498 | 0.261 | |
| k-AMH numeric++ | 0.900 | 0.487 | 0.645 | 0.689 | 0.883 | 0.455 | 0.486 | 0.262 | |
| Zk-AMH | 0.908 | 0.494 | 0.623 | 0.732 | 0.893 | 0.413 | 0.583 | 0.278 | |
| Min. | k-means | 0.373 | 0.421 | 0.307 | 0.425 | 0.332 | 0.333 | 0.185 | 0.162 |
| k-means++ | 0.495 | 0.392 | 0.320 | 0.480 | 0.486 | 0.277 | 0.181 | 0.151 | |
| Fuzzy c-means | 0.536 | 0.490 | 0.623 | 0.455 | 0.898 | 0.362 | 0.326 | 0.209 | |
| Fuzzy c-means++ | 0.457 | 0.406 | 0.310 | 0.395 | 0.456 | 0.239 | 0.255 | 0.186 | |
| k-AMH numeric | 0.884 | 0.418 | 0.619 | 0.441 | 0.705 | 0.315 | 0.435 | 0.223 | |
| k-AMH numeric++ | 0.870 | 0.472 | 0.603 | 0.451 | 0.804 | 0.297 | 0.320 | 0.205 | |
| Zk-AMH | 0.908 | 0.494 | 0.623 | 0.732 | 0.893 | 0.413 | 0.583 | 0.278 | |
| Max. | k-means | 0.844 | 0.643 | 0.729 | 0.672 | 0.880 | 0.653 | 0.467 | 0.334 |
| k-means++ | 0.829 | 0.675 | 0.714 | 0.725 | 0.885 | 0.594 | 0.458 | 0.319 | |
| Fuzzy c-means | 0.904 | 0.568 | 0.641 | 0.728 | 0.898 | 0.594 | 0.578 | 0.307 | |
| Fuzzy c-means++ | 0.960 | 0.659 | 0.723 | 0.765 | 0.911 | 0.590 | 0.659 | 0.304 | |
| k-AMH numeric | 0.928 | 0.569 | 0.696 | 0.743 | 0.904 | 0.624 | 0.595 | 0.310 | |
| k-AMH numeric++ | 0.925 | 0.512 | 0.696 | 0.752 | 0.901 | 0.624 | 0.590 | 0.306 | |
| Zk-AMH | 0.908 | 0.494 | 0.623 | 0.732 | 0.893 | 0.413 | 0.583 | 0.278 | |
| Std. Dev. | k-means | 0.118 | 0.040 | 0.136 | 0.063 | 0.125 | 0.062 | 0.057 | 0.034 |
| k-means++ | 0.101 | 0.050 | 0.071 | 0.061 | 0.112 | 0.067 | 0.060 | 0.037 | |
| Fuzzy c-means | 0.051 | 0.009 | 0.005 | 0.046 | 0.000 | 0.089 | 0.070 | 0.022 | |
| Fuzzy c-means++ | 0.126 | 0.054 | 0.086 | 0.121 | 0.129 | 0.075 | 0.086 | 0.027 | |
| k-AMH numeric | 0.009 | 0.026 | 0.028 | 0.038 | 0.020 | 0.077 | 0.047 | 0.019 | |
| k-AMH numeric++ | 0.008 | 0.009 | 0.029 | 0.066 | 0.013 | 0.079 | 0.045 | 0.023 | |
| Zk-AMH | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seman, A.; Mohd Sapawi, A. An Optimal and Stable Algorithm for Clustering Numerical Data. Algorithms 2021, 14, 197. https://0-doi-org.brum.beds.ac.uk/10.3390/a14070197
Seman A, Mohd Sapawi A. An Optimal and Stable Algorithm for Clustering Numerical Data. Algorithms. 2021; 14(7):197. https://0-doi-org.brum.beds.ac.uk/10.3390/a14070197
Chicago/Turabian StyleSeman, Ali, and Azizian Mohd Sapawi. 2021. "An Optimal and Stable Algorithm for Clustering Numerical Data" Algorithms 14, no. 7: 197. https://0-doi-org.brum.beds.ac.uk/10.3390/a14070197