A Novel Contrast Enhancement Technique on Palm Bone Images
Abstract
:1. Introduction
2. The Proposed Multi-Histogram Equalization Scheme
2.1. Global Histogram Equalization (GHE)
2.2. Multi-Histogram Equalization
3. Experimental Results and Discussion
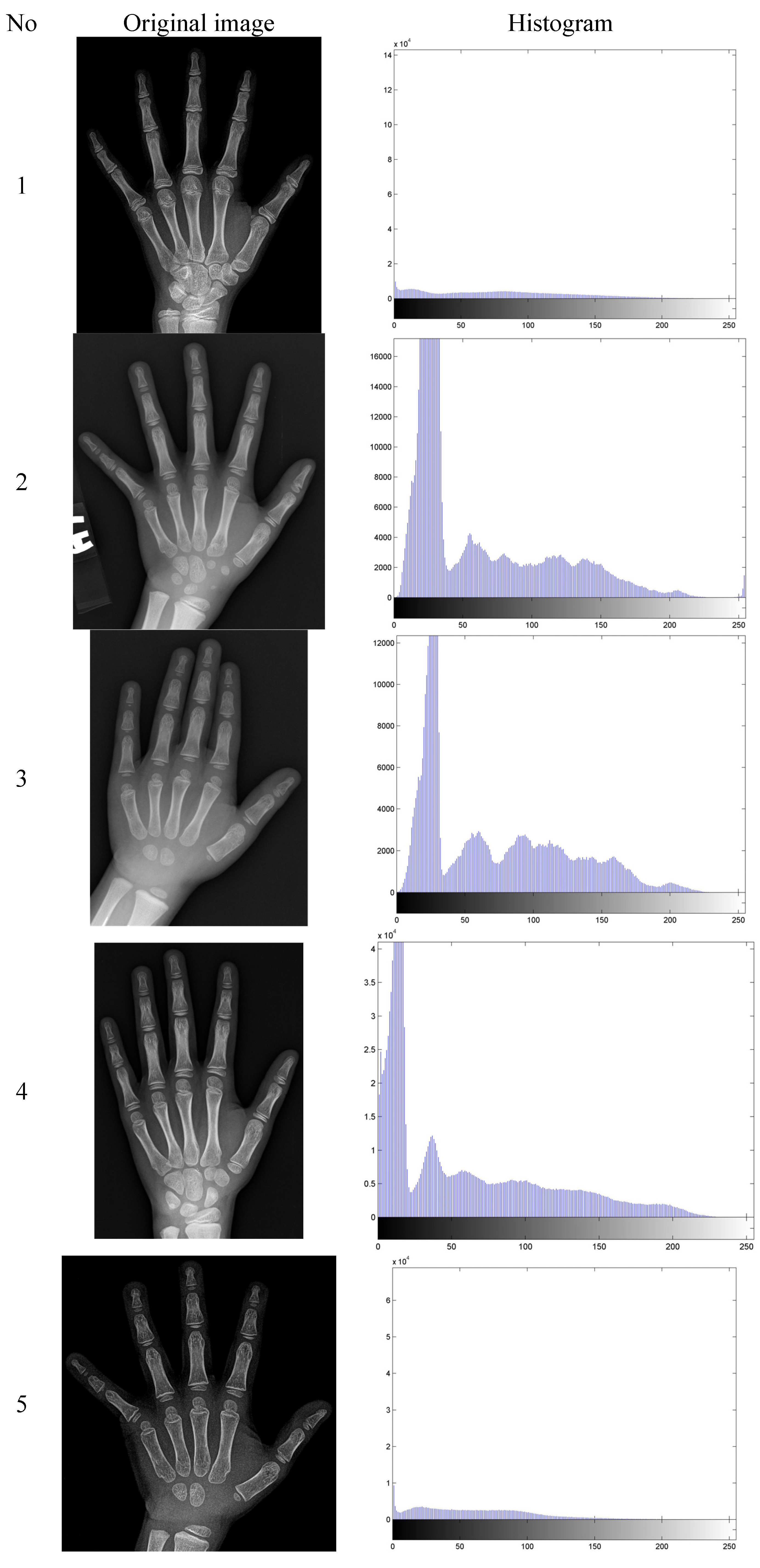
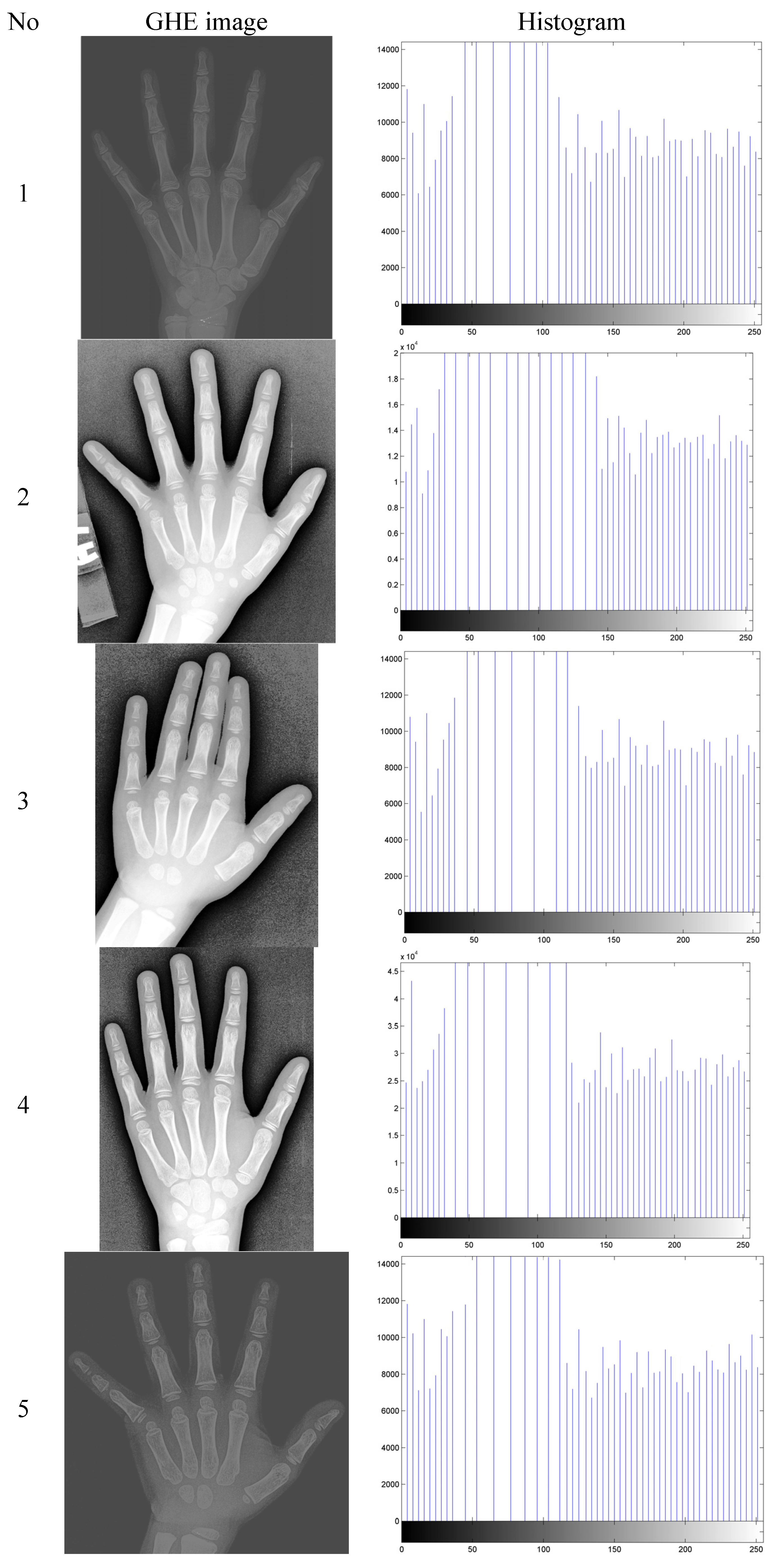
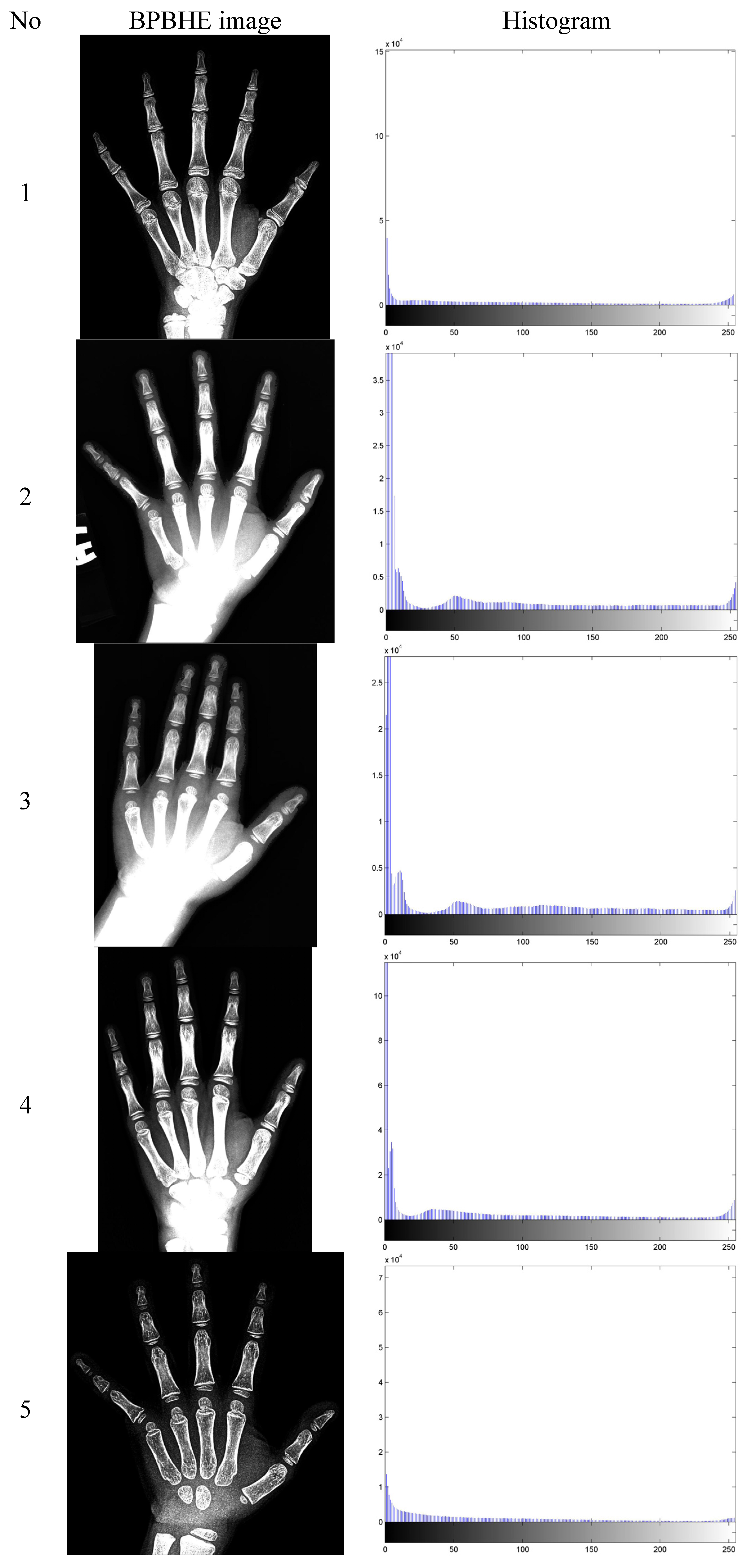

| Images | GHE | BPBHE | multi-HE |
|---|---|---|---|
| 1 | 73.28 | 10.54 | 10.57 |
| 2 | 69.94 | 5.57 | 5.06 |
| 3 | 62.86 | 11.69 | 10.50 |
| 4 | 76.35 | 9.01 | 6.71 |
| 5 | 72.00 | 4.40 | 1.05 |
| Contrast Enhance method | Average AMBE |
|---|---|
| GHE | 70.89 |
| BPBHE | 8.24 |
| multi-HE | 6.78 |
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Shin, F.Y.; Moh, J.; Bourne, H. A neural architecture applied to the enhancement of noisy binary image. Eng. Appl. Artif. Intel. 1992, 5, 215–222. [Google Scholar] [CrossRef]
- Oakley, J.P.; Bu, H. Correction of simple contrast loss in color images. IEEE Trans. Image Process. 2007, 16, 511–522. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.J.; Wang, X.D.; Duanmu, C.D. Adaptive typhoon cloud image enhancement using genetic algorithm and non-linear gain operation in undecimated wavelet domain. Eng. Appl. Artif. Intel. 2010, 23, 61–73. [Google Scholar] [CrossRef]
- Havasi, L.; Szlavik, Z.; Sziranyi, T. Detection of gait characteristics for scene registration in video surveillance system. IEEE Trans. Image Process. 2007, 16, 503–510. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.Y.; Lin, T.M.; Wolf, W.H. A visible/infrared fusion algorithm for distributed smart cameras. IEEE J. Sel. Top. Signal Process. 2008, 514–525. [Google Scholar] [CrossRef]
- Chen, D.R.; Chang, R.F.; Chen, C.J.; Ho, M.F.; Kuo, S.J.; Chen, S.T.; Hung, S.J.; Moon, W.K. Classification of breast ultrasound images using fractal feature. Clin. Imaging 2005, 29, 235–245. [Google Scholar] [CrossRef] [PubMed]
- Bemmel, C.M.; Wink, O.; Verdonck, B.; Viergever, M.A.; Niessen, W.J. Blood pool contrast-enhanced MRA: improved arterial visualization in the steady state. IEEE Trans. Med. Imaging 2003, 22, 645–652. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 2nd ed.; Prentice Hall: New Jersey, NJ, USA, 2002. [Google Scholar]
- Abdullah-Al-Wadud, M.; Kabir, M.H.; Dewan, M.A.A.; Chae, O. A dynamic histogram equalization for image contrast enhancement. IEEE Trans. Consum. Electron. 2007, 53, 593–600. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Abidi, B.R.; Page, D.L.; Abidi, M.A. Graylevel grouping (GLG): An automatic method for optimized image contrast enhancement-part. ii: the variations. IEEE Trans. Image Process. 2006, 15, 2303–2314. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.Y.; Kim, L.S.; Hwang, S.H. An advanced contrast enhancement using partially overlapped sub-block histogram equalization. IEEE Trans. Circuits Syst. Video Technol. 2001, 11, 475–484. [Google Scholar]
- Lamberti, F.; Montrucchio, B.; Sanna, A. CMBFHE: A novel contrast enhancement technique based on cascaded multistep binomial filtering histogram equalization. IEEE Trans. Consum. Electron. 2006, 52, 966–974. [Google Scholar] [CrossRef]
- Umbaugh, S.E. Computer Vision and Image Processing; Prentice Hall: New Jersey, NJ, USA, 1998. [Google Scholar]
- Kim, Y.T. Contrast enhancement using brightness preserving Bi-Histogram equalization. IEEE Trans. Consum. Electron. 1997, 43, 1–8. [Google Scholar]
- Wang, Y.; Chen, Q.; Zhang, B. Image enhancement based on equal area dualistic sub-image histogram equalization method. IEEE Trans. on Consum. Electron. 1999, 45, 68–75. [Google Scholar] [CrossRef]
- Chen, S.D.; Ramli, Abd. R. Minimum mean brightness error bi-histogram equalization in contrast enhancement. IEEE Trans. Consum. Electron. 2003, 49, 1310–1319. [Google Scholar] [CrossRef]
- Wang, C.; Ye, Z. Brightness preserving histogram equalization with maximum entropy: A variational perspective. IEEE Trans. Consum. Electron. 2005, 51, 1326–1334. [Google Scholar] [CrossRef]
- Menotti, D.; Najman, L.; Facon, J.; Araujo, A.A. Multi-histogram equalization methods for contrast enhancement and brightness preserving. IEEE Trans. Consum. Electron. 2007, 53, 1186–1194. [Google Scholar] [CrossRef]
- Kong, N.S.P.; Ibrahim, H.D. Color image enhancement using brightness preserving dynamic histogram equalization. IEEE Trans. Consum. Electron. 2008, 54, 1962–1968. [Google Scholar] [CrossRef]
- Park, G.H.; Cho, H.H.; Choi, M.R. A contrast enhancement method using dynamic range separate histogram equalization. IEEE Trans. Consum. Electron. 2008, 54, 1981–1987. [Google Scholar] [CrossRef]
- Kim, T.; Paik, J. Adaptive contrast enhancement using gain-controllable clipped histogram equalization. IEEE Trans. Consum. Electron. 2008, 54, 1803–1810. [Google Scholar] [CrossRef]
- Chen, S.D.; Ramli, A.R. Contrast enhancement using recursive mean separate histogram equalization for scalable brightness preservation. IEEE Trans.Consum. Electron. 2003, 49, 1301–1309. [Google Scholar] [CrossRef]
- Sim, K.S.; Tso, C.P.; Tan, Y.Y. Recursive sub-image histogram equalization applied to gray scale images. Pattern Recognit. Letters 2007, 28, 1209–1221. [Google Scholar] [CrossRef]
- Abdullah-Al-Wadud, M.; Kabir, M.H.; Dewan, M.A.A.; Oksam, C. A dynamic histogram equalization for image contrast enhancement. IEEE Trans. Consum. Electron. 2007, 53, 593–600. [Google Scholar] [CrossRef]
- Ibrahim, H.; Kong, N.S.P. Brightness preserving dynamic histogram equalization for image contrast enhancement. IEEE Trans. Consum. Electron. 2007, 53, 1752–1758. [Google Scholar] [CrossRef]
- Manpreet, K.; Jasdeep, K.; Jappreet, K. Survey of contrast enhancement techniques based on histogram equalization. Int. J. Adv. Comput. Sci. Appl. 2011, 2, 137–141. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Chang, Y.-T.; Wang, J.-T.; Yang, W.-H. A Novel Contrast Enhancement Technique on Palm Bone Images. Algorithms 2014, 7, 444-455. https://0-doi-org.brum.beds.ac.uk/10.3390/a7030444
Chang Y-T, Wang J-T, Yang W-H. A Novel Contrast Enhancement Technique on Palm Bone Images. Algorithms. 2014; 7(3):444-455. https://0-doi-org.brum.beds.ac.uk/10.3390/a7030444
Chicago/Turabian StyleChang, Yung-Tsang, Jen-Tse Wang, and Wang-Hsai Yang. 2014. "A Novel Contrast Enhancement Technique on Palm Bone Images" Algorithms 7, no. 3: 444-455. https://0-doi-org.brum.beds.ac.uk/10.3390/a7030444




