In this section, the proposed WFCS algorithm has been evaluated by a large number of experiments performed on the simulated dataset and the real dataset. The real datasets include eight UCI benchmarking datasets [
14] and a CFM56-type engine dataset (named as ENGINE (ENGINE data can be provided by sending email to the corresponding author)) with measurement noise which has been collected from Air Company. In order to obtain the simulated data, an aero-engine gas path data with Gauss noise (named as LTT) was obtained by a simulation software (developed by the Laboratory of Thermal Turbo machines at the National Technical University of Athens (Downloaded from
http://www.ltt.mech.ntua.gr/index.php/softwaremn/teachesmn)). The ENGINE and the LTT datasets present the aero-engine’s states, including healthy states and degrade states. In these experiments, all datasets are normalized into (0, 1) [
13].
First, the datasets information, validation criteria and parameters setting are described. Then, the properties of the WFCS are investigated based on the experimental results of the Iris dataset. A detailed comparison with other three feature weighting fuzzy clustering algorithms (ESSC, WFCM, WSRFCM) and one un-weighted fuzzy clustering algorithm (FCS) is performed at last.
3.2. Property Analysis of WFCS
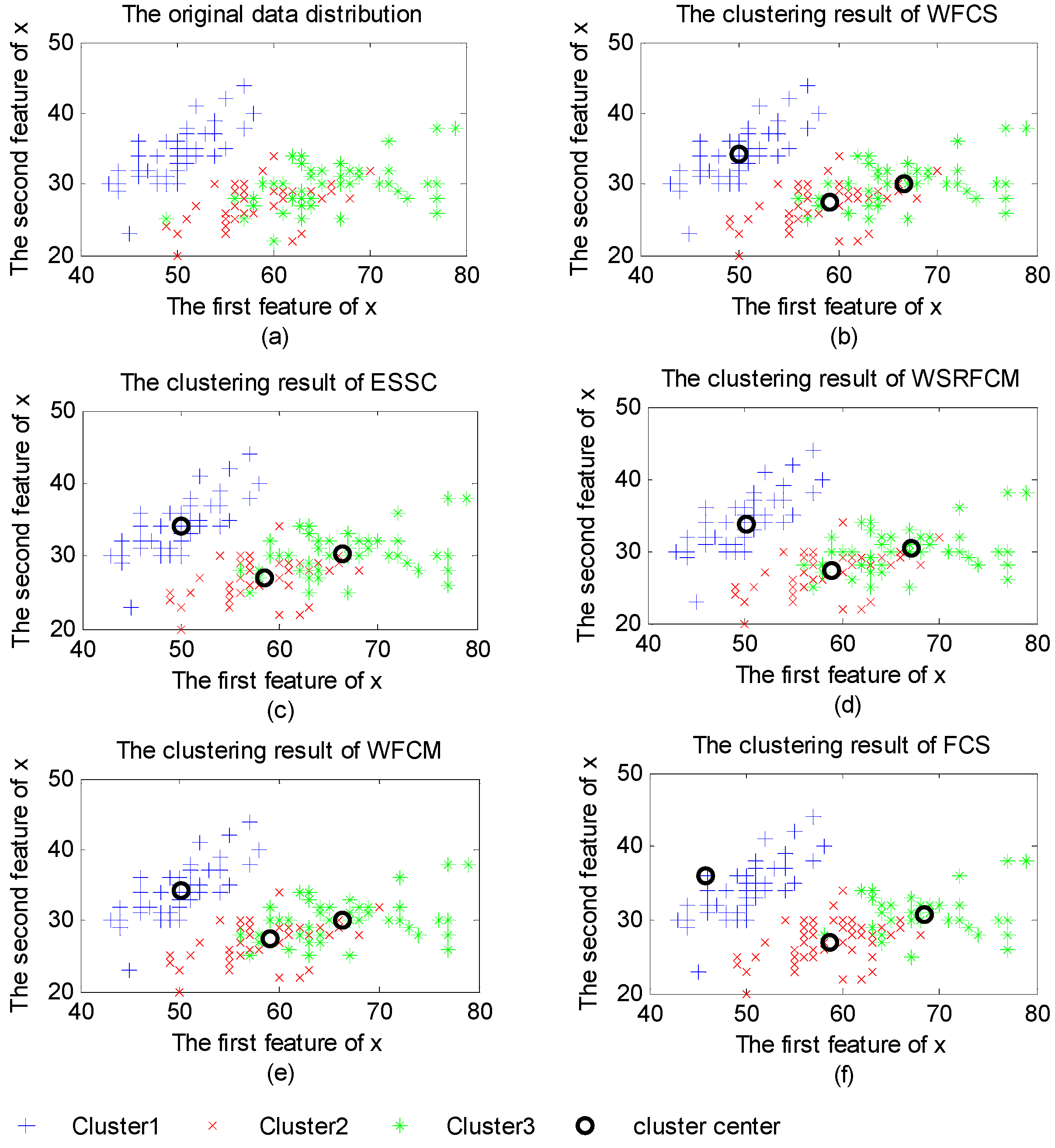
Figure 2 demonstrates the original distribution of Iris dataset and the clustering results of the five algorithms. As shown in
Figure 2a, Iris dataset contains three clusters of 50 data points each, where each cluster refers to a type of iris plant. It is obvious that Cluster1 is linearly separable from the other two while the latters are overlapped. Hence, it is more reasonable for data points in Cluster1 to be hard clustered than to be fuzzy clustered.
(1) Clustering performance
Figure 2 shows that clustering results of feature weighted clustering algorithms (WFCS, ESSC, WFCM and WSRFCM) are similar to the distribution of original data (shown in
Figure 2 (a)). Data points in Cluster1 can be recognized very well by the five algorithms. Moreover, most data points in Cluster2 and Cluster3 can be recognized by the four feature weighted algorithms. In
Figure 2 (f), it is obvious that some data in Cluster3 are misclassified into Cluster2 by FCS.
The cluster centers of five algorithms are different from each other. Furthermore, the distance between Cluster1, Cluster2 and Cluster3 center obtained by the five algorithms are shown in
Figure 3.
With regard to WFCS, ESSC and FCS integrating the within-cluster compactness and between-cluster separation, the distances between the overlapped Cluster2 and Cluster3 center are larger than that of WSRFCM and WFCM. However, FCS can’t partition the data points belonging to Cluster2 or Cluster3 correctly for it has not included the feature weight though the biggest value of distance is obtained.
Figure 2.
(a) The original data distribution; (b) The clustering results of weighting fuzzy compactness and separation algorithm (WFCS); (c) The clustering results of enhanced soft subspace clustering algorithm (ESSC); (d) The clustering results of the feature weighting fuzzy clustering algorithm integrating rough sets and shadowed sets (WSRFCM); (e) The clustering results of the feature weighting fuzzy c-means algorithm (WFCM); (f) The clustering results of the fuzzy compactness and separation algorithm (FCS).
Figure 2.
(a) The original data distribution; (b) The clustering results of weighting fuzzy compactness and separation algorithm (WFCS); (c) The clustering results of enhanced soft subspace clustering algorithm (ESSC); (d) The clustering results of the feature weighting fuzzy clustering algorithm integrating rough sets and shadowed sets (WSRFCM); (e) The clustering results of the feature weighting fuzzy c-means algorithm (WFCM); (f) The clustering results of the fuzzy compactness and separation algorithm (FCS).
Figure 3.
The distance between three cluster centers.
Figure 3.
The distance between three cluster centers.
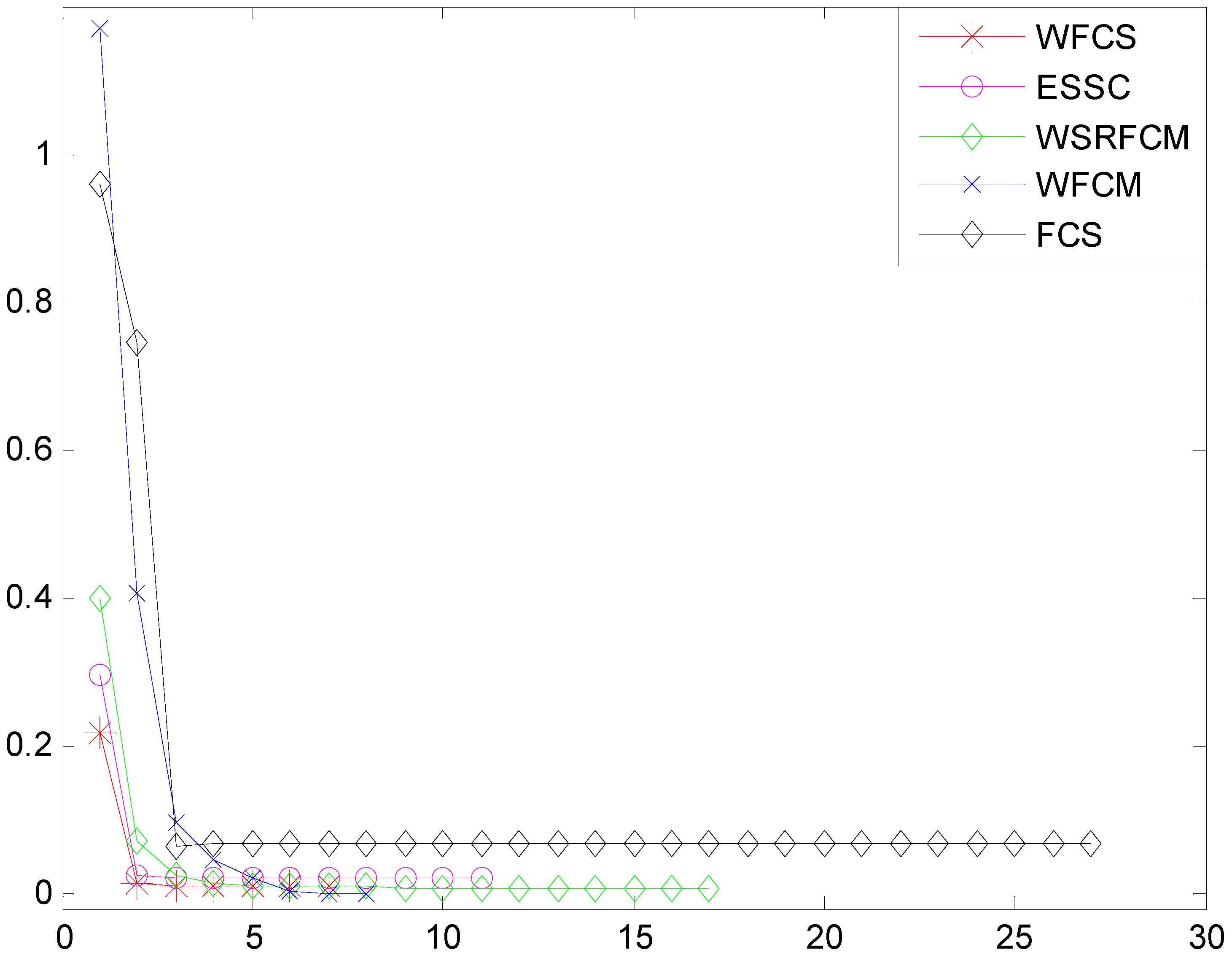
Since different clustering algorithms have different objective functions, we introduce the iteration function in order to evaluate the convergence of algorithm.
Figure 4 shows the convergence curves of the five algorithms.
Figure 4.
Convergence of the five algorithms.
Figure 4.
Convergence of the five algorithms.
As shown in
Figure 4, the five convergence curves descend fast in the first two iterations, and the convergence curves vary slowly after three iterations. Furthermore, the smaller iteration number means the higher convergence speed. Overall, WFCS has a higher speed of convergence. The convergence speed of WFCM is lower than that of WFCS and ESSC, while the FCS has the lowest convergence speed.
(2) Hard clustering
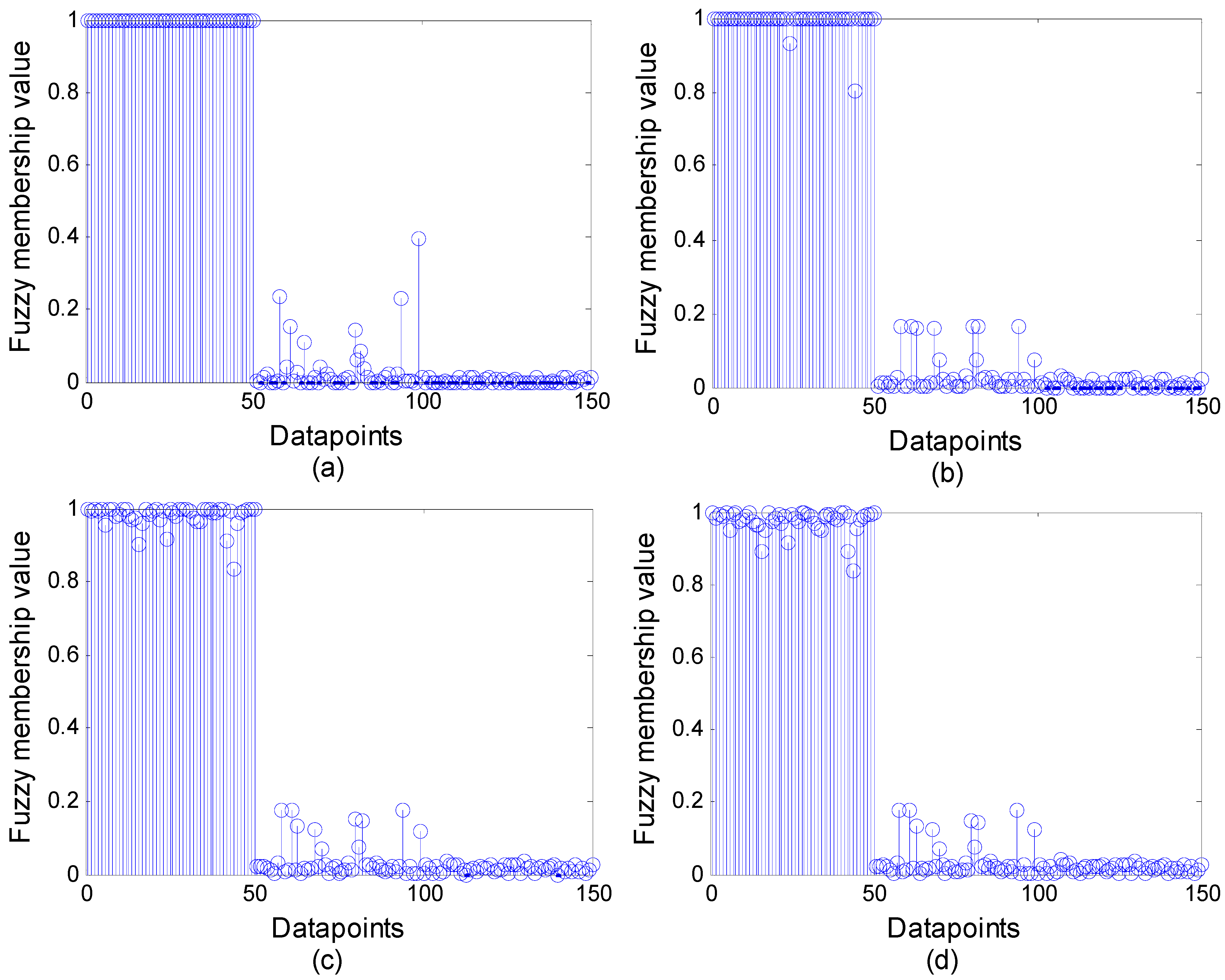
Figure 5 shows the fuzzy membership values for Cluster1 of 150 data points in WFCS when
is 1, 0.5, 0.05 and 0.005 respectively. When membership value is equal to 1, data point is hard clustered into Cluster1. When membership value is 0, data point is hard clustered into the other two clusters.
In
Figure 5a–c, there are 50, 31 and 12 data points hard clustered into Cluster1 respectively. In
Figure 5d, all data point membership values are smaller than 1, then all data points are fuzzy clustered into Cluster1. As seen in
Figure 5, the membership value becomes fuzzier when
is smaller. Hence, WFCS has the characteristics of both hard clustering and fuzzy clustering.
3.3. Clustering Evaluation
The best RI indexes of the five algorithms are presented in
Table 4.
Figure 5.
Fuzzy membership value on the first cluster with different (a) ; (b) ; (c) ; (d) .
Figure 5.
Fuzzy membership value on the first cluster with different (a) ; (b) ; (c) ; (d) .
It is evident in
Table 4 that WFCS demonstrates the best performance except for Breast-cancer, Vehicle and ENGINE datasets. The performance of WFCM and WSRFCM are mostly comparable or better than that of ESSC and FCS. Even if FCS is not a feature weighted clustering algorithm, it is able to achieve the best clustering result performance for the dataset Wine.
Table 5 and
Table 6 list the XB and WB index values of the five algorithms respectively. By comparing
Table 4,
Table 5 and
Table 6, we found that the best clustering performance as indicated through RI is not always the smallest value as indicated through XB or WB index. Therefore, no single algorithm can always be superior to the others for all datasets.
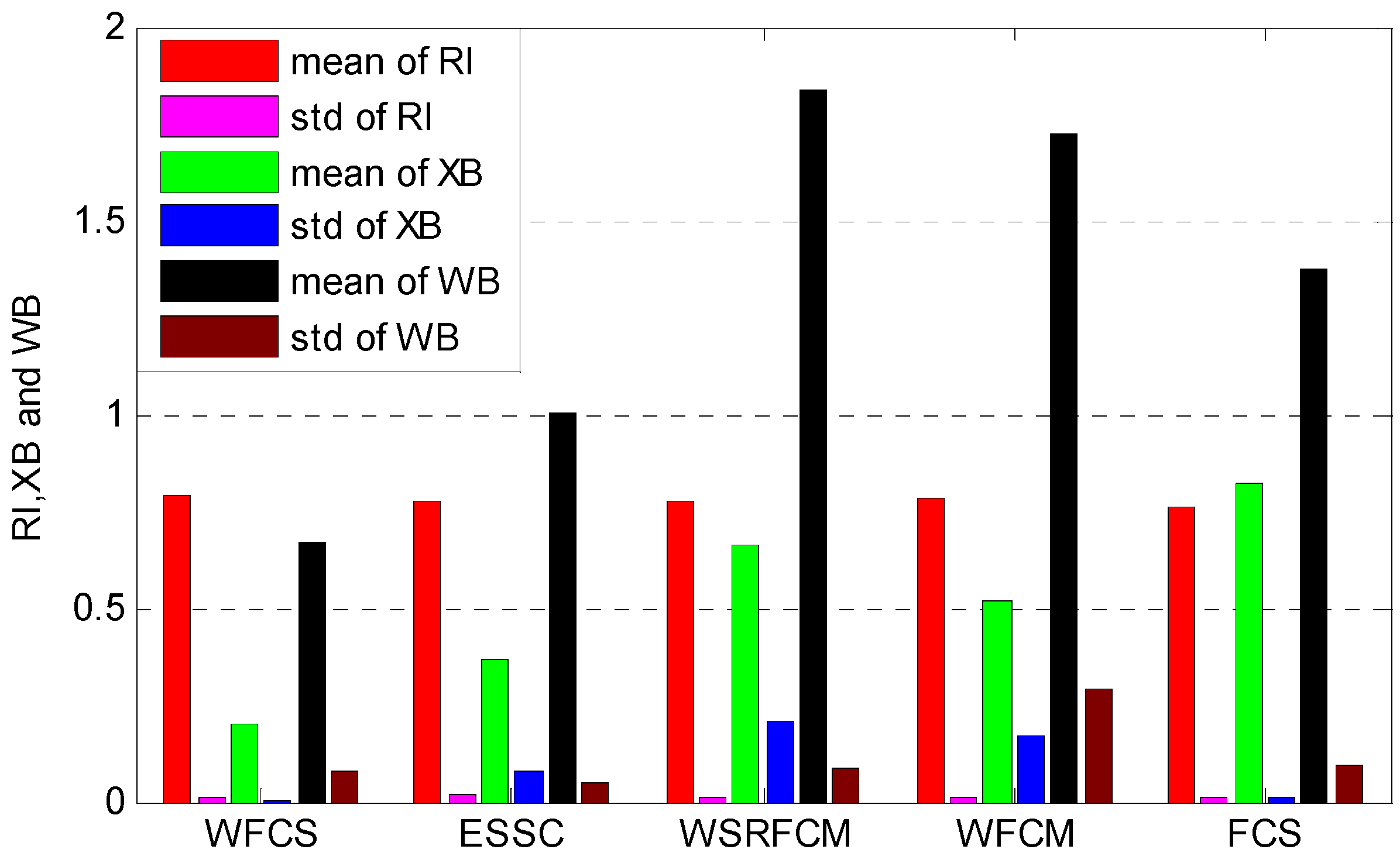
The average performances of the five algorithms are shown in
Figure 6.
Figure 6.
The average performances of the five algorithms.
Figure 6.
The average performances of the five algorithms.
Table 4.
The best clustering results obtained for the 10 datasets with rand index (RI).
Table 4.
The best clustering results obtained for the 10 datasets with rand index (RI).
| Dataset | WFCS | ESSC | WSRFCM | WFCM | FCS |
|---|
| Australian |
| mean | 0.7336 | 0.7162 | 0.7302 | 0.7265 | 0.6995 |
| std | 0.0000 | 0.1134 | 0.0033 | 0.0569 | 0.0125 |
| Breast Cancer |
| mean | 0.8721 | 0.8779 | 0.8630 | 0.8600 | 0.8627 |
| std | 0.0009 | 0.0057 | 0 | 0.0000 | 0.0000 |
| Balance-scale |
| mean | 0.6427 | 0.6389 | 0.6101 | 0.6099 | 0.6201 |
| std | 0.0758 | 0.0287 | 0.0586 | 0.0578 | 0.0662 |
| Heart |
| mean | 0.7163 | 0.7114 | 0.7120 | 0.6939 | 0.6833 |
| std | 0.0000 | 0.0019 | 0.0023 | 0.0000 | 0.0000 |
| Iris |
| mean | 0.9495 | 0.9195 | 0.9495 | 0.9495 | 0.8679 |
| std | 0.0000 | 0.0000 | 0.0081 | 0.0000 | 0.0000 |
| Pima |
| mean | 0.5841 | 0.5564 | 0.5698 | 0.5837 | 0.5576 |
| std | 0.0000 | 0.0005 | 0.0044 | 0.0009 | 0.0000 |
| Vehicle |
| mean | 0.6654 | 0.6539 | 0.6778 | 0.6581 | 0.6528 |
| std | 0.0025 | 0.0028 | 0.0006 | 0.0038 | 0.0000 |
| Wine |
| mean | 0.9551 | 0.9398 | 0.9324 | 0.9398 | 0.9551 |
| std | 0.0000 | 0.0095 | 0.0000 | 0.0000 | 0.0000 |
| ENGINE |
| mean | 0.8600 | 0.7823 | 0.7693 | 0.8600 | 0.7903 |
| std | 0.0000 | 0.0005 | 0.0067 | 0.0000 | 0.0000 |
| LTT |
| mean | 0.9671 | 0.96 | 0.9543 | 0.9671 | 0.9607 |
| std | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
Table 5.
Xie-Beni (XB) index of algorithms.
Table 5.
Xie-Beni (XB) index of algorithms.
| Dataset | WFCS | ESSC | WSRFCM | WFCM | FCS |
|---|
| Australian |
| mean | 0.0400 | 0.7194 | 1.4636 | 1.2056 | 0.1995 |
| std | 0.0007 | 0.3455 | 0.8407 | 1.0488 | 0.0267 |
| Breast Cancer |
| mean | 0.3216 | 0.2961 | 0.4288 | 0.3270 | 0.1094 |
| std | 0.0021 | 0.0344 | 0.0903 | 0.0003 | 0.0000 |
| Balance-scale |
| mean | 0.4435 | 0.7051 | 0.6970 | 0.7392 | 2.8475 |
| std | 0.0000 | 0.0248 | 0.0287 | 0.0725 | 0.0979 |
| Heart |
| mean | 0.1593 | 0.4033 | 0.7942 | 0.6348 | 0.2267 |
| std | 0.0081 | 0.0982 | 0.7522 | 0.5030 | 0.0000 |
| Iris |
| mean | 0.0844 | 0.0861 | 0.2700 | 0.1964 | 0.2922 |
| std | 0.0019 | 0.0059 | 0.0226 | 0.0000 | 0.0000 |
| Pima |
| mean | 0.1443 | 0.4942 | 0.7610 | 0.5955 | 0.4759 |
| std | 0.0002 | 0.0235 | 0.1977 | 0.0406 | 0.0000 |
| Vehicle |
| mean | 0.2532 | 0.2601 | 0.8538 | 0.5480 | 3.2949 |
| std | 0.0000 | 0.0917 | 0.0372 | 0.0047 | 0.0097 |
| Wine |
| mean | 0.2577 | 0.3970 | 0.6775 | 0.4987 | 0.4061 |
| std | 0.0034 | 0.0009 | 0.0640 | 0.0000 | 0.0000 |
| ENGINE |
| mean | 0.1699 | 0.1836 | 0.3755 | 0.2130 | 0.1267 |
| std | 0.0030 | 0.0685 | 0.0295 | 0.0217 | 0.0000 |
| LTT |
| mean | 0.1019 | 0.1075 | 0.3299 | 0.2131 | 0.2105 |
| std | 0.0014 | 0.0983 | 0.0029 | 0.0000 | 0.0000 |
In
Figure 6, we can see that WFCS obtained the best mean values of RI (0.7946) and XB (0.1976) with the least standard variation (0.0079, 0.0021 respectively) for the 10 datasets. WFCM, WSRFCM and ESSC perform similarly in terms of RI. It can be seen that the feature weighting clustering algorithms are superior to the un-weighted clustering one. The average XB and WB index values of WFCS, ESSC and FCS are smaller than those of WFCM and WSRFCM, which demonstrate that these three algorithms integrating between-cluster separation and within-cluster compactness can partition data points more reasonably.
Table 6.
Within-Between(WB) index of algorithms.
Table 6.
Within-Between(WB) index of algorithms.
| Dataset | WFCS | ESSC | WSRFCM | WFCM | FCS |
|---|
| Australian |
| mean | 0.0551 | 0.1730 | 0.6312 | 0.7261 | 0.5971 |
| std | 0.0000 | 0.1313 | 0.0011 | 0.4054 | 0.2144 |
| Breast Cancer |
| mean | 0.3849 | 0.3843 | 0.5388 | 0.6035 | 0.4510 |
| std | 0.0010 | 0.0084 | 0.0000 | 0.0000 | 0.0000 |
| Balance-scale |
| mean | 2.1924 | 3.6567 | 5.8354 | 6.1232 | 5.6191 |
| std | 0.7932 | 0.1983 | 0.0911 | 0.1686 | 0.7135 |
| Heart |
| mean | 1.1191 | 1.1191 | 2.3297 | 3.3005 | 1.8087 |
| std | 0.0000 | 0.0991 | 0.0012 | 0.0000 | 0.0000 |
| Iris |
| mean | 0.0729 | 0.3300 | 0.8423 | 0.6224 | 0.5366 |
| std | 0.0079 | 0.0097 | 0.6452 | 0.0311 | 0.0000 |
| Pima |
| mean | 0.2828 | 0.6195 | 1.0043 | 0.4897 | 0.4832 |
| std | 0.0012 | 0.0003 | 0.0627 | 0.0073 | 0.0000 |
| Vehicle |
| mean | 0.1908 | 0.2850 | 0.5000 | 0.4128 | 0.6351 |
| std | 0.0010 | 0.0087 | 0.0149 | 0.0000 | 0.0000 |
| Wine |
| mean | 0.9821 | 0.9934 | 2.0174 | 1.4317 | 0.8599 |
| std | 0.0038 | 0.0350 | 0.0028 | 0.0000 | 0.0000 |
| ENGINE |
| mean | 0.4866 | 0.8500 | 1.6315 | 1.6072 | 0.8484 |
| std | 0.0079 | 0.0060 | 0.0056 | 2.3408 | 0.0000 |
| LTT |
| mean | 0.9206 | 1.6253 | 3.0179 | 1.9023 | 1.8894 |
| std | 0.0075 | 0.0281 | 0.0106 | 0.0002 | 0.0000 |