Training Artificial Neural Networks by a Hybrid PSO-CS Algorithm
Abstract
:1. Introduction
2. Previous Works
3. The Hybrid PSOCS Algorithm
3.1. Particle Swarm Optimization
3.2. Cuckoo Search Algorithm

3.3. The Proposed Algorithm
- The cuckoos near good solutions try to communicate with the other cuckoos that are exploring a different part of the search space.
- When all cuckoos are near good solutions, they move slowly. Under the circumstances, gbest helps them to exploit the global best.
- The algorithm uses gbest to memorize the best solution found so far, and it can be accessed at any time.
- Each cuckoo can see the best solution (gbest) and has the tendency to go toward it.
- The abilities of local searching and global searching can be balanced by adjusting c′1 and c′2.
- Finally, by adjusting the values of pa and in each iteration, the convergence rates of the PSOCS are improved.
4. Training FNNs
4.1. The One Hidden Layer FNN Architecture
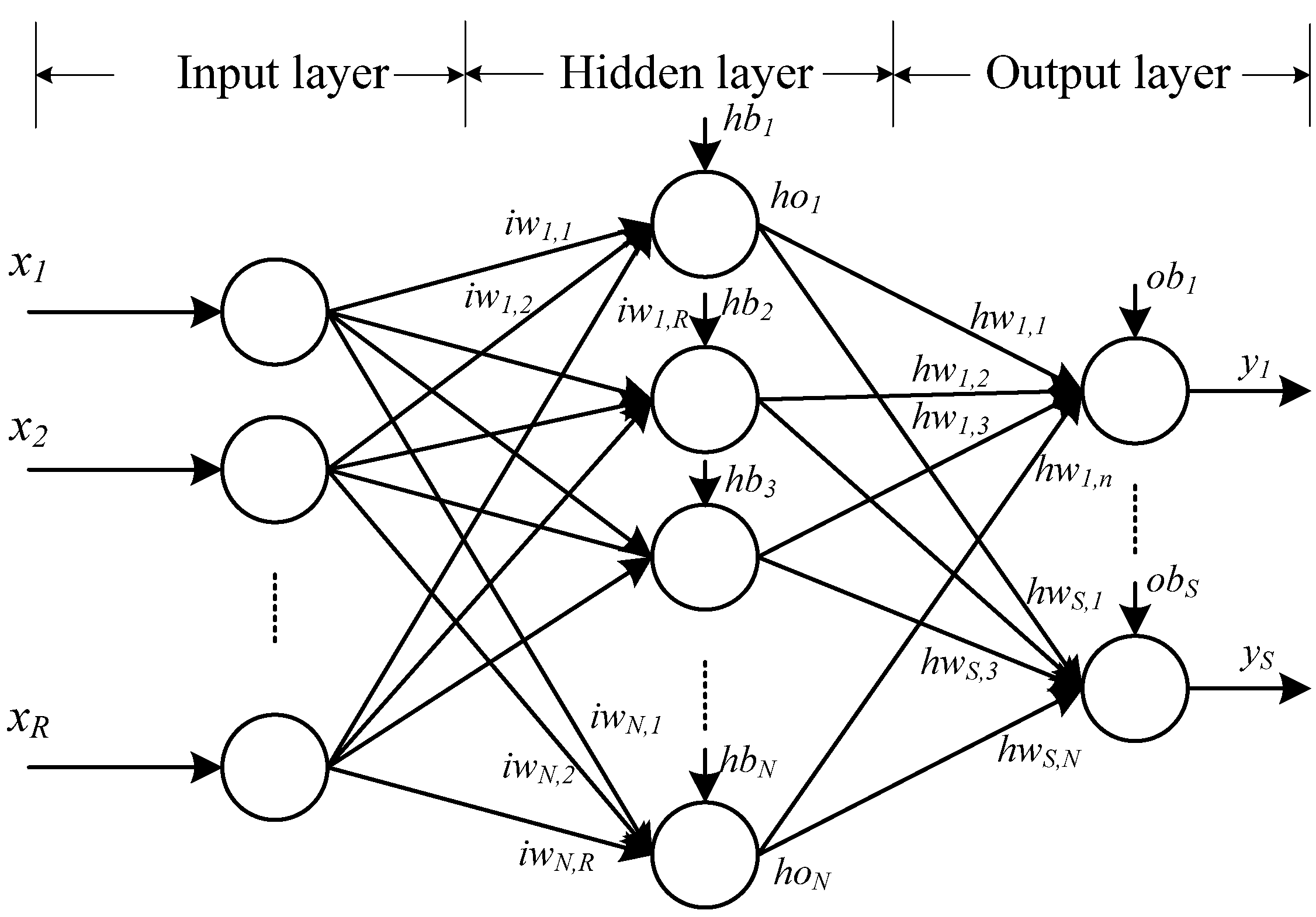
4.2. Training Method
4.3. Encoding Strategy

4.4. Criteria for Evaluating Performance
5. Experimental Results
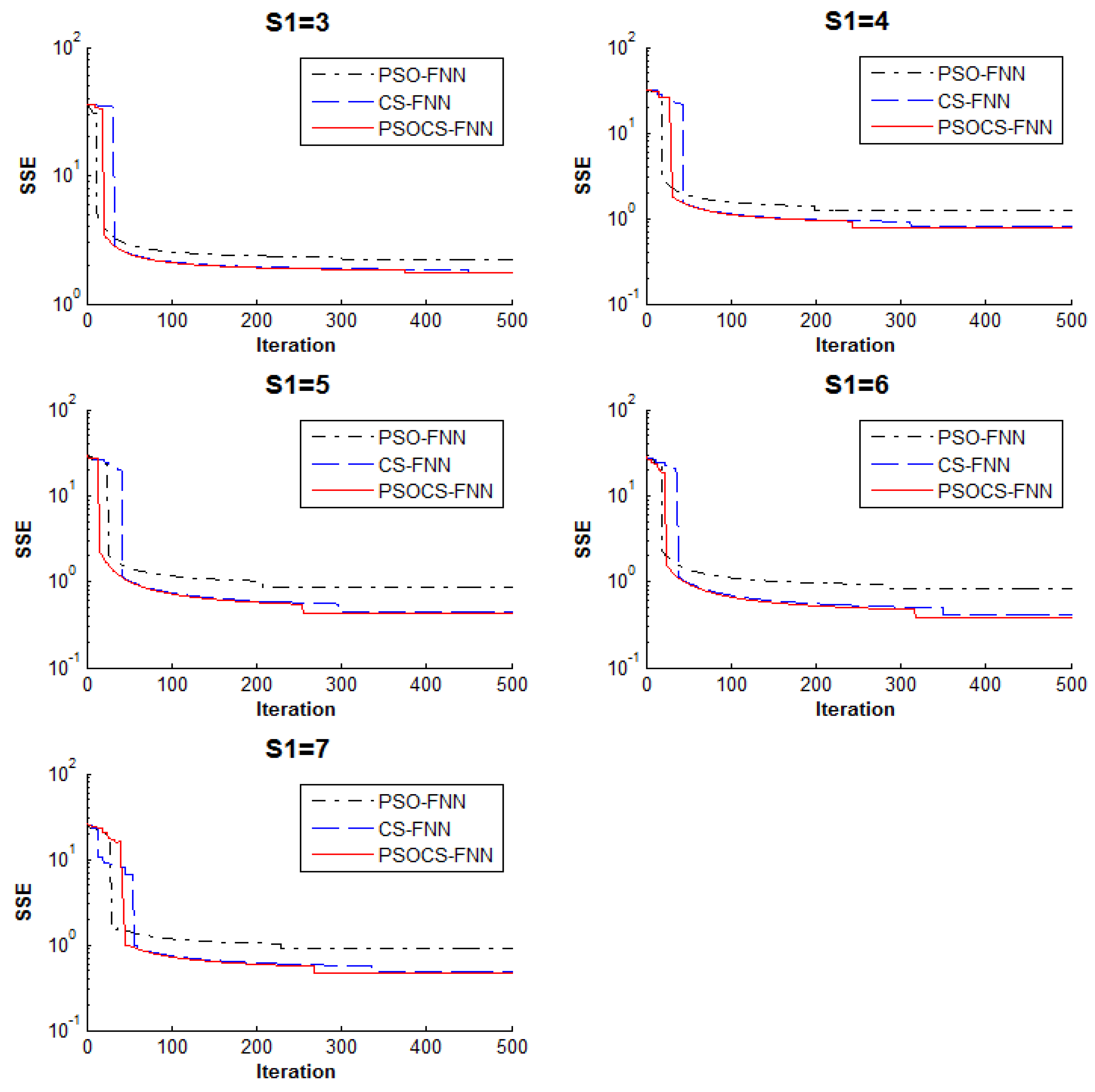
5.1. Experiment 1: Approximation Problem
| Hidden Node (S1) | Algorithm | SSE | |||
|---|---|---|---|---|---|
| Min | Average | Max | Std. Dev. | ||
| 3 | PSO | 1.504569 | 2.197208 | 2.64631 | 0.462301 |
| CS | 1.064576 | 1.765316 | 2.212237 | 0.463635 | |
| PSOCS | 1.047247 | 1.737105 | 2.166139 | 0.457843 | |
| 4 | PSO | 0.861025 | 1.225908 | 1.736935 | 0.348625 |
| CS | 0.414418 | 0.810047 | 1.323472 | 0.360855 | |
| PSOCS | 0.427326 | 0.790218 | 1.27989 | 0.342118 | |
| 5 | PSO | 0.691495 | 0.875569 | 1.299515 | 0.250296 |
| CS | 0.286534 | 0.453186 | 0.877309 | 0.248645 | |
| PSOCS | 0.253777 | 0.430846 | 0.822753 | 0.233818 | |
| 6 | PSO | 0.513046 | 0.828988 | 0.969032 | 0.181192 |
| CS | 0.127328 | 0.414455 | 0.554916 | 0.167307 | |
| PSOCS | 0.088938 | 0.384225 | 0.512852 | 0.171315 | |
| 7 | PSO | 0.619243 | 0.91505 | 1.150879 | 0.190815 |
| CS | 0.206532 | 0.48647 | 0.670016 | 0.170129 | |
| PSOCS | 0.155654 | 0.462798 | 0.725362 | 0.202521 | |
5.2. Experiment 2: Classification Problem
| Hidden Node (S2) | Algorithm | SSE | Training Accuracy | Testing Accuracy |
|---|---|---|---|---|
| 4 | PSO | 39.39494 | 0.794 | 0.76 |
| CS | 34.353 | 0.824 | 0.776 | |
| PSOCS | 34.21615 | 0.866 | 0.788 | |
| 5 | PSO | 38.52052 | 0.81 | 0.792 |
| CS | 33.29272 | 0.836 | 0.824 | |
| PSOCS | 33.1576 | 0.854 | 0.8 | |
| 6 | PSO | 37.81462 | 0.82 | 0.744 |
| CS | 32.06983 | 0.826 | 0.824 | |
| PSOCS | 31.92559 | 0.838 | 0.788 | |
| 7 | PSO | 34.48936 | 0.818 | 0.8 |
| CS | 29.9164 | 0.868 | 0.888 | |
| PSOCS | 29.77234 | 0.872 | 0.816 | |
| 8 | PSO | 33.87586 | 0.814 | 0.804 |
| CS | 28.26575 | 0.844 | 0.852 | |
| PSOCS | 28.14429 | 0.876 | 0.824 | |
| 9 | PSO | 31.9543 | 0.83 | 0.816 |
| CS | 26.24346 | 0.852 | 0.824 | |
| PSOCS | 26.10769 | 0.878 | 0.832 | |
| 10 | PSO | 31.13578 | 0.83 | 0.84 |
| CS | 25.40347 | 0.852 | 0.84 | |
| PSOCS | 25.25101 | 0.9 | 0.864 | |
| 11 | PSO | 30.12397 | 0.8 | 0.824 |
| CS | 24.69134 | 0.866 | 0.86 | |
| PSOCS | 24.57097 | 0.87 | 0.876 | |
| 12 | PSO | 28.62928 | 0.868 | 0.856 |
| CS | 22.72357 | 0.876 | 0.848 | |
| PSOCS | 22.57407 | 0.94 | 0.872 | |
| 13 | PSO | 28.14103 | 0.828 | 0.828 |
| CS | 21.52259 | 0.836 | 0.88 | |
| PSOCS | 21.38662 | 0.952 | 0.896 | |
| 14 | PSO | 26.44765 | 0.888 | 0.804 |
| CS | 20.3495 | 0.888 | 0.848 | |
| PSOCS | 20.21154 | 0.982 | 0.948 | |
| 15 | PSO | 28.36295 | 0.82 | 0.816 |
| CS | 23.45967 | 0.832 | 0.832 | |
| PSOCS | 23.31919 | 0.928 | 0.84 |

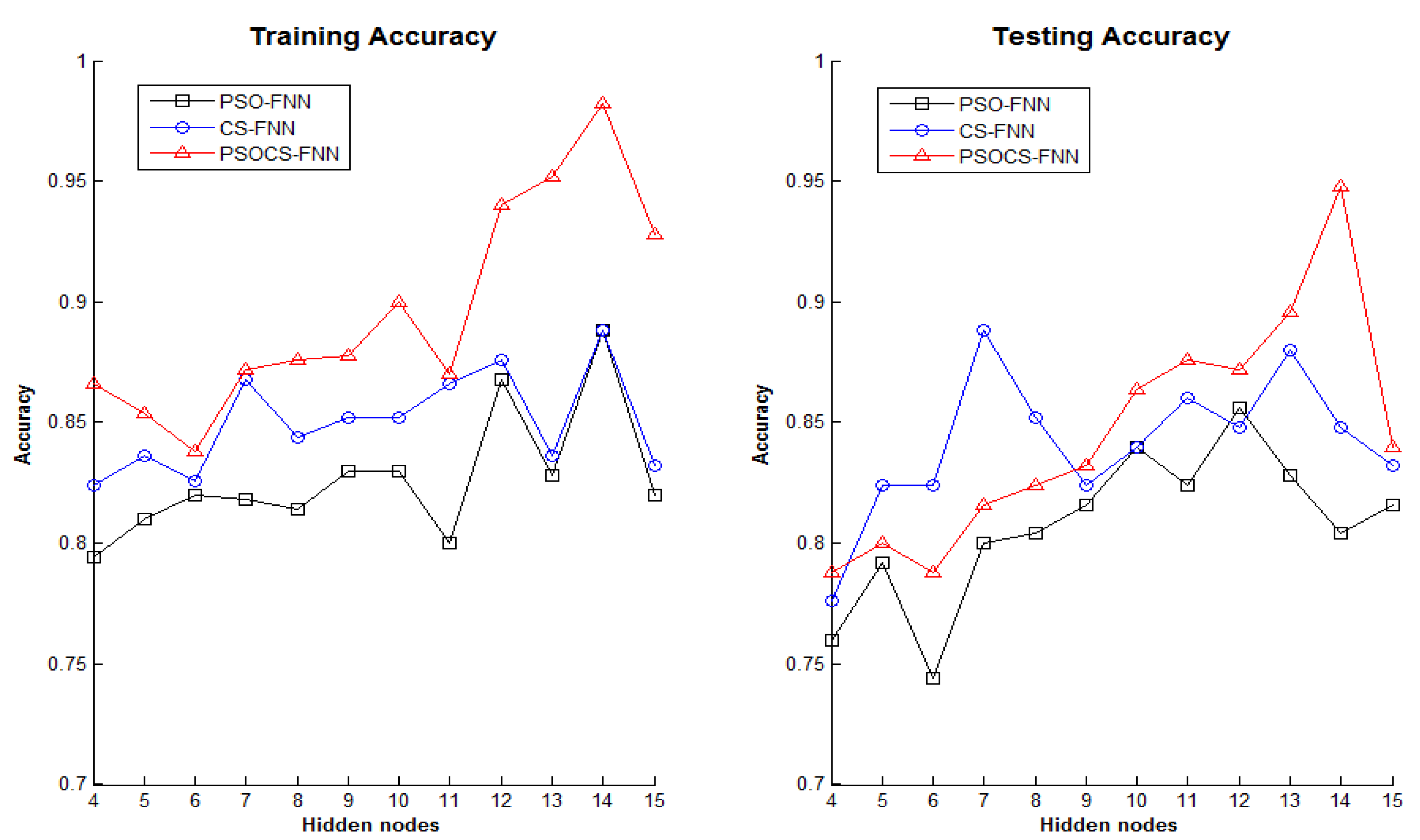
6. Conclusions
Acknowledgment
Author Contributions
Conflicts of Interest
References
- Paliwal, M.; Kumar, U.A. Neural networks and statistical techniques: A review of applications. Expert Syst. Appl. 2009, 36, 2–17. [Google Scholar] [CrossRef]
- Vosniakos, G.C.; Benardos, P.G. Optimizing feedforward Artificial Neural Network Architecture. Eng. Appl. Artif. Intell. 2007, 20, 365–382. [Google Scholar]
- Funahashi, K. On the approximate realization of continuous mappings by neural networks. Neural Netw. 1989, 2, 183–192. [Google Scholar] [CrossRef]
- Norgaard, M.R.O.; Poulsen, N.K.; Hansen, L.K. Neural Networks for Modeling and Control of Dynamic Systems. A Practitioner’s Handbook; Springer: London, UK, 2000. [Google Scholar]
- Mat Isa, N. Clustered-hybrid multilayer perceptron network for pattern recognition application. Appl. Soft Comput. 2011, 11, 1457–1466. [Google Scholar] [CrossRef]
- Homik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar]
- Malakooti, B.; Zhou, Y. Approximating polynomial functions by feedforward artificial neural network: Capacity analysis and design. Appl. Math. Comput. 1998, 90, 27–52. [Google Scholar] [CrossRef]
- Hush, R.; Horne, N.G. Progress in supervised neural networks. IEEE Signal Proc. Mag. 1993, 10, 8–39. [Google Scholar] [CrossRef]
- Hagar, M.T.; Menhaj, M.B. Training feedforward networks with the Marquardt algorithm. IEEE Trans. Neural Netw. 1994, 5, 989–993. [Google Scholar]
- Adeli, H.; Hung, S.L. An adaptive conjugate gradient learning algorithm for efficient training of neural networks. Appl. Math. Comput. 1994, 62, 81–102. [Google Scholar] [CrossRef]
- Zhang, N. An online gradient method with momentum for two-layer feedforward neural networks. Appl. Math. Comput. 2009, 212, 488–498. [Google Scholar] [CrossRef]
- Gupta, J.N.D.; Sexton, R.S. Comparing backpropagation with a genetic algorithm for neural network training. Omega 1999, 27, 679–684. [Google Scholar] [CrossRef]
- Mirjalili, S.A.; Mohd Hashim, S.Z.; Sardroudi, H.M. Training feedforward neural networks using hybrid particle swarm optimization and gravitational search algorithm. Appl. Math. Comput. 2012, 218, 11125–11137. [Google Scholar] [CrossRef]
- Gori, M.; Tesi, A. On the problem of local minima in back-propagation. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 76–86. [Google Scholar] [CrossRef]
- Zhang, J.R.; Zhang, J.; Lock, T.M.; Lyu, M.R. A hybrid particle swarm optimization–back-propagation algorithm for feedforward neural network training. Appl. Math. Comput. 2007, 185, 1026–1037. [Google Scholar] [CrossRef]
- Goldberg, E. Genetic Algorithms in Search, Optimization and Machine Learning; Addison Wesley: Boston, MA, USA, 1989. [Google Scholar]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the 1995 IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948.
- Dorigo, M.; Maniezzo, V.; Golomi, A. Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybernet. 1996, 26, 29–41. [Google Scholar] [CrossRef] [PubMed]
- Cells, M.; Rylander, B. Neural network learning using particle swarm optimizers. In Advances in Information Science and Soft Computing; WSEAS Press: Cancun, Mexico, 2002; pp. 224–226. [Google Scholar]
- Yang, X.S.; Deb, S. Cuckoo search via Lévy flights. In Proceedings of the IEEE World Congress on Nature and Biologically Inspired Computing (NaBIC 2009), Coimbatore, India, 9–11 December 2009; pp. 210–214.
- Yang, X.S.; Deb, S. Engineering Optimisation by Cuckoo Search. Int. J. Math. Model. Numer. Optim. 2010, 1, 330–343. [Google Scholar] [CrossRef]
- Valian, E.; Mohanna, S.; Tavakoli, S. Improved Cuckoo Search Algorithm for Feedforward Neural Network Training. Int. J. Artif. Intell. Appl. 2009, 2, 36–43. [Google Scholar]
- Ouaarab, A.; Ahiod, B.; Yang, X.S. Discrete cuckoo search algorithm for the travelling salesman problem. Neural Comput. Appl. 2014, 24, 1659–1669. [Google Scholar] [CrossRef]
- Zhou, Y.; Zheng, H. A novel complex valued Cuckoo Search algorithm. Sci. World J. 2013. [Google Scholar] [CrossRef] [PubMed]
- Li, L.K.; Shao, S.; Yiu, K.F.C. A new optimization algorithm for single hidden layer feedforward neural networks. Appl. Soft Comput. 2013, 13, 2857–2862. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Ince, T.; Yildirim, A.; Gabbouj, M. Evolutionary artificial neural networks by multi-dimensional particle swarm optimization. Neural Netw. 2009, 22, 1448–1462. [Google Scholar] [CrossRef] [PubMed]
- Mirjalili, S.; Hashim, S.Z.M. A New Hybrid PSOGSA Algorithm for Function Optimization. In Proceedings of the International Conference on Computer and Information Application (ICCIA 2010), Tianjin, China, 3–5 December 2010; pp. 374–377.
- Rashedi, E.; Nezamabadi-pour, H.; Saryazdi, S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Civicioglu, P. Transforming Geocentric Cartesian Coordinates to Geodetic Coordinates by Using Differential Search Algorithm. Comput. Geosci. 2012, 46, 229–247. [Google Scholar] [CrossRef]
- Civicioglu, P. Artificial cooperative search algorithm for numerical optimization problems. Inf. Sci. 2013, 229, 58–76. [Google Scholar] [CrossRef]
- Civicioglu, P.; Besdok, E. A conceptual comparison of the cuckoo-search, particle swarm optimization, differential evolution and artificial bee colony algorithms. Artif. Intell. Rev. 2013, 39, 315–346. [Google Scholar] [CrossRef]
- Civicioglu, P. Backtracking Search Optimization Algorithm for numerical optimization problems. Appl. Math. Comput. 2013, 219, 8121–8144. [Google Scholar] [CrossRef]
- Lai, X.; Zhang, M. An efficient ensemble of GA and PSO for real function optimization. In Proceedings of 2nd IEEE International Conference on Computer Science and Information Technology, Beijing, China, 8–11 August 2009; pp. 651–655.
- Esmin, A.A.A.; Lambert-Torres, G.; Alvarenga, G.B. Hybrid Evolutionary Algorithm Based on PSO and GA mutation. In Proceeding of the Sixth International Conference on Hybrid Intelligent Systems (HIS 06), Auckland, New Zealand, 13–15 December 2006; p. 57.
- Li, L.; Xue, B.; Niu, B.; Tan, L.; Wang, J. A Novel PSO-DE-Based Hybrid Algorithm for Global Optimization. Lect. Notes Comput. Sci. 2007, 785–793. [Google Scholar]
- Holden, N.; Freitas, A.A. A Hybrid PSO/ACO Algorithm for Discovering Classification Rules in Data Mining. J. Artif. Evolut. Appl. 2008. [Google Scholar] [CrossRef]
- Ghodrati, A.; Lotfi, S. A Hybrid CS/PSO Algorithm for Global Optimization, Intelligent Information and Database Systems. Lect. Notes Comput. Sci. Vol. 2012, 7198, 89–98. [Google Scholar]
- Yang, X.S.; Deb, S. Cuckoo Search: Recent Advances and Applications. Neural Comput. Appl. 2014, 24, 169–174. [Google Scholar] [CrossRef]
- Caruana, R.; Lawrence, S.; Giles, C.L. Overfitting in neural networks: Backpropagation, conjugate gradient, and early stopping. In Advances Neural Information Processing Systems; Leen, T.K., Dietterich, T.G., Tresp, V., Eds.; MIT Press: Denver, CO, USA, 2000; Volume 13, pp. 402–408. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.-F.; Do, Q.H.; Hsieh, H.-N. Training Artificial Neural Networks by a Hybrid PSO-CS Algorithm. Algorithms 2015, 8, 292-308. https://0-doi-org.brum.beds.ac.uk/10.3390/a8020292
Chen J-F, Do QH, Hsieh H-N. Training Artificial Neural Networks by a Hybrid PSO-CS Algorithm. Algorithms. 2015; 8(2):292-308. https://0-doi-org.brum.beds.ac.uk/10.3390/a8020292
Chicago/Turabian StyleChen, Jeng-Fung, Quang Hung Do, and Ho-Nien Hsieh. 2015. "Training Artificial Neural Networks by a Hybrid PSO-CS Algorithm" Algorithms 8, no. 2: 292-308. https://0-doi-org.brum.beds.ac.uk/10.3390/a8020292






