MAKHA—A New Hybrid Swarm Intelligence Global Optimization Algorithm
Abstract
:1. Introduction
2. The Monkey Algorithm (MA)
- 1)
- The climb process: In this exploitation process, monkeys search the local optimum solution extensively in a close range.
- 2)
- The watch-jump process: In this process, monkeys look for new solutions with objective value higher than the current ones. It is considered an exploitation and intensification method.
- 3)
- The somersault process: This process is for exploration and it prevents getting trapped in a local optimum. Monkeys search for new points in other search domains. In nature, each monkey attempts to reach the highest mountaintop, which corresponds to the maximum value of the objective function. The fitness of the objective function simulates the height of the mountaintop, while the decision variable vector is considered to contain the positions of the monkeys. Changing the sign of the objective function allows the algorithm to find the global minimum instead of the global maximum. The pseudo-code for this algorithm is shown in Figure 1.

- a)
- Random generation of α from the somersault interval [c, d] where c and d governs the maximum distance that the monkey can somersault.
- b)
- Create a pivot P by the following equation:where , NP is the population number and X is the monkey position.
- c)
- Get y (Monkey new position) from
- d)
- Update Xi with Yi if feasible (within boundary limits) or repeat until feasible.
3. The Krill Herd Algorithm (KHA)
- a)
- The movement induced by the presence of other individuals.
- b)
- The foraging activity.
- c)
- Random diffusion.

4. MAKHA Hybrid Algorithm
- The watch-jump process.
- The foraging activity process.
- The physical random diffusion process.
- The genetic mutation and crossover process.
- The somersault process.

- Initialization procedure:
- -
- Random generation of population in which the positions of the hybrid agent (monkey/krill) are created randomly, Xi = (Xi1, Xi2, …, Xi(NV)) where i = 1 to NP, which represents the number of hybrids, while NV represents the dimension of the decision variable vector.
- The fitness evaluation and sorting:
- -
- Hi=f(Xi) where H stands for hybrid fitness and f is the objective function used.
- The watch-jump process:
- -
- Random generation of Xi from (Xij − b, Xij + b) where b is the eyesight of the hybrid (monkey in MA) which indicates the maximal distance the hybrid can watch and Yi = (Yi1, Yi2, …, Yi(NV)), which are the new hybrid positions.
- -
- If −f (Yi) ≥ −f (Xi) then update Xi with Yi if feasible (i.e., within limits).
- Foraging motion:
- -
- Depends on food location and the previous experience about the location.
- -
- Calculate the food attractive and the effect of best fitness so farwhere Cfood is the food coefficient, which decreases with time and is calculated from:where I is the iteration number and Imax is the maximum number of iterations.
- -
- The center of food density is estimated from the following equation:and Hibest is the best previously visited position.
- -
- and are unit normalized values obtained from this general form:where ε is a small positive number that is added to avoid singularities. Hbest and Hworst are the best and the worst fitness values, respectively, of the hybrid agents so far. H stands for the hybrid fitness and was used as K symbol in krill herd method.
- -
- The foraging motion is defined aswhere Vf is the foraging speed, wf is the inertia weight of the foraging motion in the range [0, 1], and is the last foraging motion.
- Physical diffusion:This is an exploration step that is used at high dimensional problem, thenwhere Dmax is the maximum diffusion speed and δ is the random direction vector.
- Calculate the time interval Δtwhere Ct is constant.
- The step for position is calculated through:where represents the velocity of the hybrid agent (Krill/Monkey).
- Implementation of genetic operator:
- -
- Crossoverwhere and Cr is the crossover probability
- -
- Mutationwhere µ is a random number, and Mu is the mutation probability:where Hgb is the best global fitness of the hybrid so far and Xgbest is its position.
- The somersault process:
- -
- α is generated randomly from [c, d] where c and d are somersault interval. Two different implementations of the somersault process can be used:Somersault I
- -
- -
- Update Xi with Y if feasible or repeat until feasible.Somersault II
- -
- Create a pivot P by this equation used in MA:
- -
- Get Y (i.e., the hybrid new position)
- -
- Update Xi with Y if feasible and repeat until feasible.
5. Numerical Experiments
| Name | Objective Function | ||
|---|---|---|---|
| Ackley [34] | |||
| Beale [35] | |||
| Bird [36] | |||
| Booth [35] | |||
| Bukin 6 [35] | |||
| Carrom table [37] | |||
| Cross-leg table [37] | |||
| Generalized egg holder [35] | |||
| Goldstein–Price [38] | |||
| Himmelblau [39] | |||
| Levy 13 [40] | |||
| Schaffer [37] | |||
| Zettl [41] | |||
| Helical valley [42] | , | ||
| Powell [43] | |||
| Wood [44] | |||
| Extended Cube [45] | |||
| Shekel 5*[46] | |||
| Sphere [47] | |||
| Hartman 6 * [48] | |||
| Griewank [49] | |||
| Rastrigin [50] | |||
| Rosenbrock [51] | |||
| Sine envelope sine wave [37] | |||
| Styblinski–Tang [52] | |||
| Trigonometric [53] | |||
| Zacharov [54] | |||
| Objective Function | NV | Search Domain | Global Minimum | Iterations | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MA | KHA | MAKHA | ||||||||
| Ackley | 2 | [−35, 35] | 0 | 25 | 3000 | 1000 | ||||
| Beale | 2 | [−4.5, 4.5] | 0 | 25 | 3000 | 1000 | ||||
| Bird | 2 | [−2π, 2π] | −106.765 | 25 | 3000 | 1000 | ||||
| Booth | 2 | [−10, 10] | 0 | 25 | 3000 | 1000 | ||||
| Bukin 6 | 2 | [−15, 3] | 0 | 25 | 3000 | 1000 | ||||
| Carrom table | 2 | [−10, 10] | −24.15681 | 25 | 3000 | 1000 | ||||
| Cross-leg table | 2 | [−10, 10] | −1 | 25 | 3000 | 1000 | ||||
| Generalized egg holder | 2 | [−512, 512] | −959.64 | 124 | 15,000 | 5000 | ||||
| Goldstein-Price | 2 | [−2, 2] | 3 | 25 | 3000 | 1000 | ||||
| Himmelblau | 2 | [−5, 5] | 0 | 25 | 3000 | 1000 | ||||
| Levy 13 | 2 | [−10, 10] | 0 | 25 | 3000 | 1000 | ||||
| Schaffer | 2 | [−100, 100] | 0 | 199 | 15,000 | 8000 | ||||
| Zettl | 2 | [−5, 5] | −0.003791 | 25 | 3000 | 1000 | ||||
| Helical valley | 3 | [−1000, 1000] | 0 | 25 | 3000 | 1000 | ||||
| Powell | 4 | [−1000, 1000] | 0 | 50 | 6000 | 2000 | ||||
| Wood | 4 | [−1000, 1000] | 0 | 25 | 3000 | 1000 | ||||
| Extended Cube | 5 | [−100, 100] | 0 | 25 | 3000 | 1000 | ||||
| Shekel 5 | 4 | [0, 10] | −10.1532 | 25 | 3000 | 1000 | ||||
| Sphere | 5 | [−100, 100] | 0 | 75 | 9000 | 1000 | ||||
| Hartman 6 | 6 | [0,1] | −3.32237 | 25 | 3000 | 1000 | ||||
| Griewank | 50 | [−600, 600] | 0 | 124 | 15000 | 5000 | ||||
| Rastrigin | 50 | [−5.12, 5.12] | 0 | 124 | 15000 | 5000 | ||||
| Rosenbrock | 50 | [−50, 50] | 0 | 124 | 15000 | 5000 | ||||
| Sine envelope sine wave | 50 | [−100, 100] | 0 | 124 | 15000 | 5000 | ||||
| Styblinski-Tang | 50 | [−5,5] | −1958.2995 | 124 | 15000 | 5000 | ||||
| Trigonometric | 50 | [−1000, 1000] | 0 | 124 | 15000 | 5000 | ||||
| Zacharov | 50 | [−5,10] | 0 | 25 | 3000 | 1000 | ||||
| Method | Condition | Parameter | Selected value |
|---|---|---|---|
| MA | b | 1 | |
| R ≥ 100 | b | 10 | |
| c | −1 | ||
| d | 1 | ||
| R ≥ 500 | c | −10 | |
| R ≥ 500 | d | 30 | |
| NC | 30 | ||
| KHA | Dmax | [0.002, 0.01] | |
| Ct | 0.5 | ||
| Vf | 0.02 | ||
| Nmax | 0.01 | ||
| wf and wN | [0.1, 0.8] | ||
| MAKHA I | b | 1 | |
| R < 2 | b | 0.5*R | |
| R ≥ 100 | b | 10 | |
| c | −0.1 | ||
| d | 0.1 | ||
| Dmax | 0 | ||
| Ct | 0.5 | ||
| Vf | 0.2 | ||
| wf | 0.1 | ||
| Somersault I is used | |||
| MAKHA II (NV = 50) | b | 0.3*R | |
| c | −R | ||
| d | R | ||
| Dmax | [0.002, 0.01] | ||
| Ct | 0.5 | ||
| Vf | 0.02 | ||
| wf | [0.1, 0.8] | ||
| Somersault II is used | |||
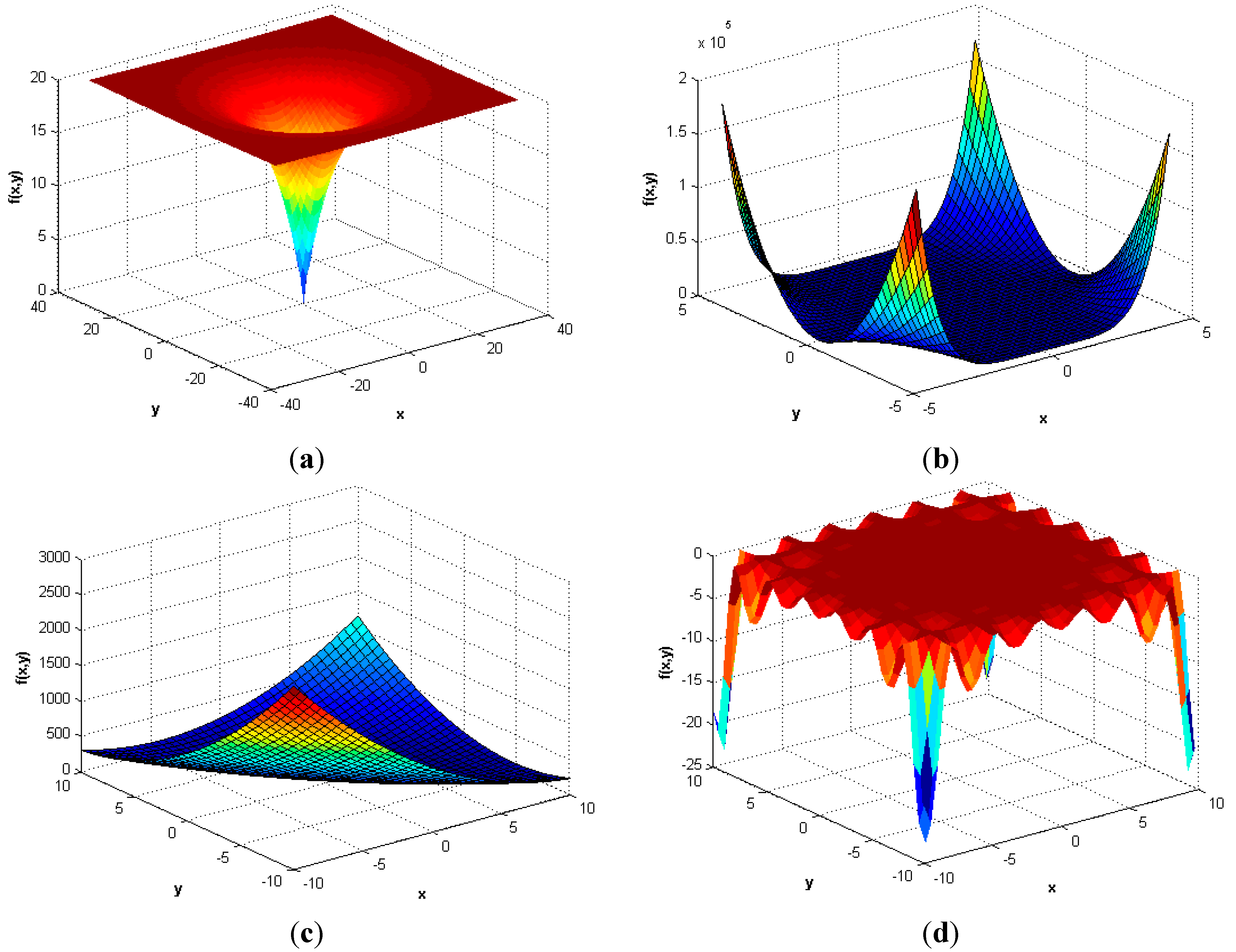
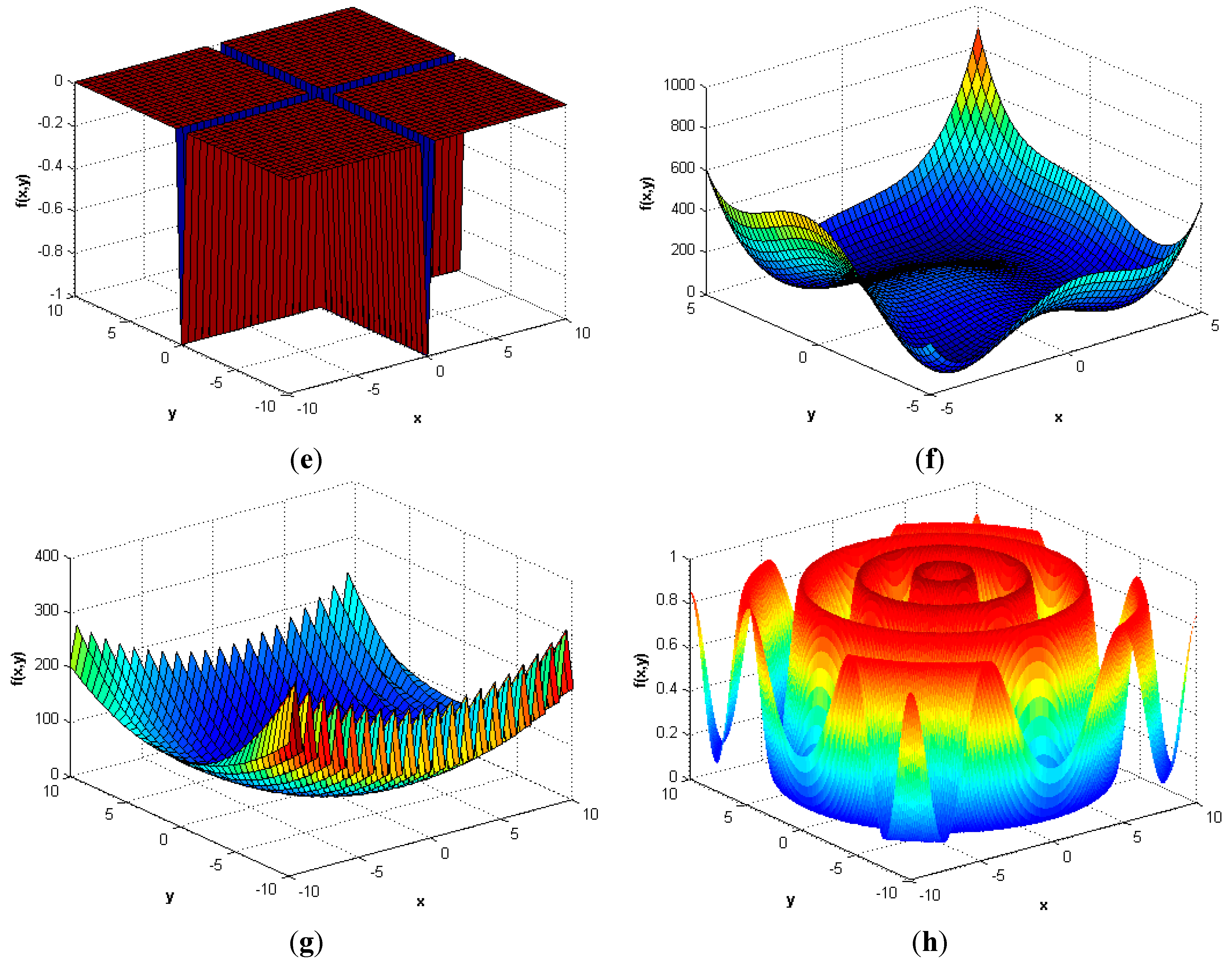
6. Results and Discussion
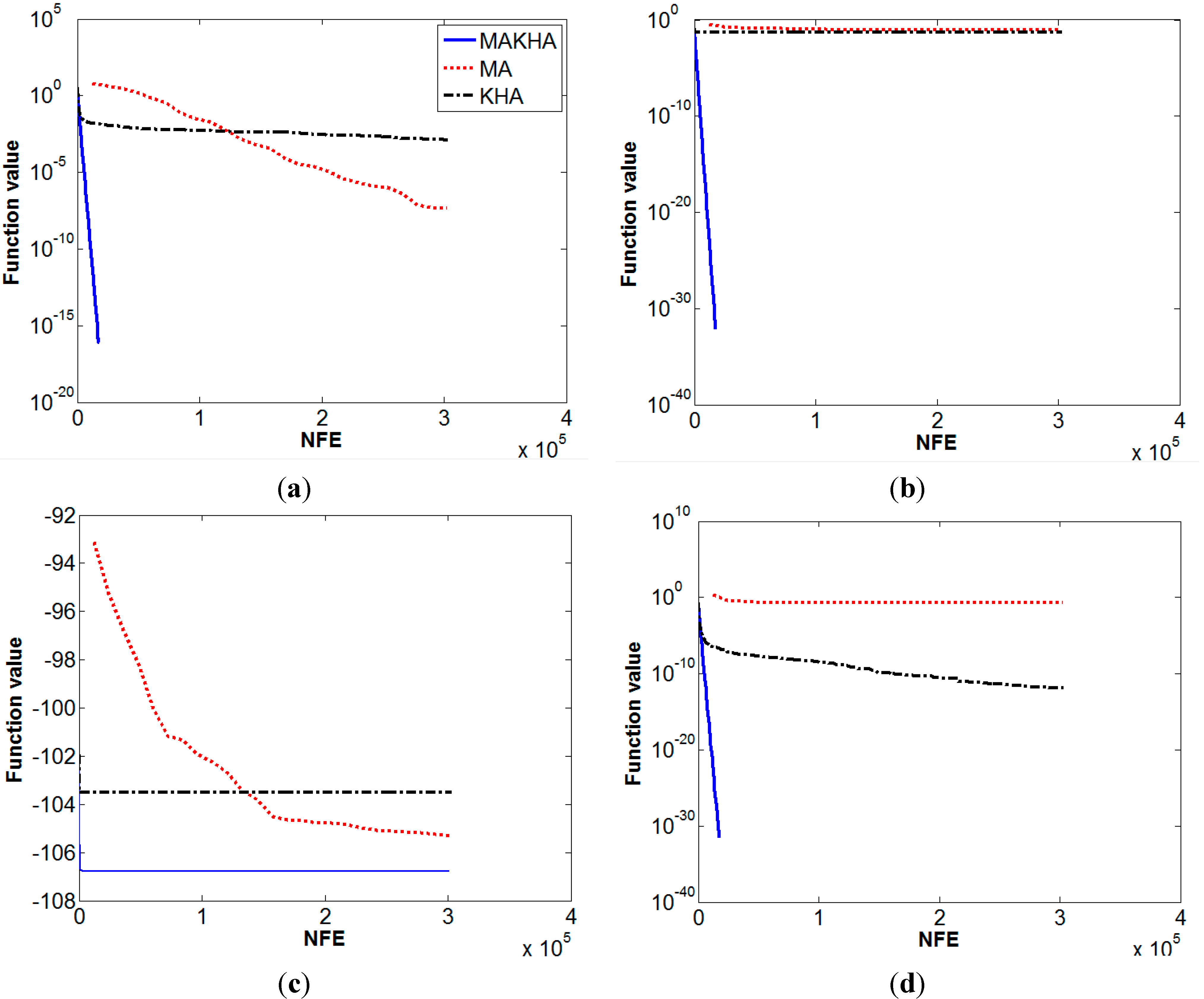
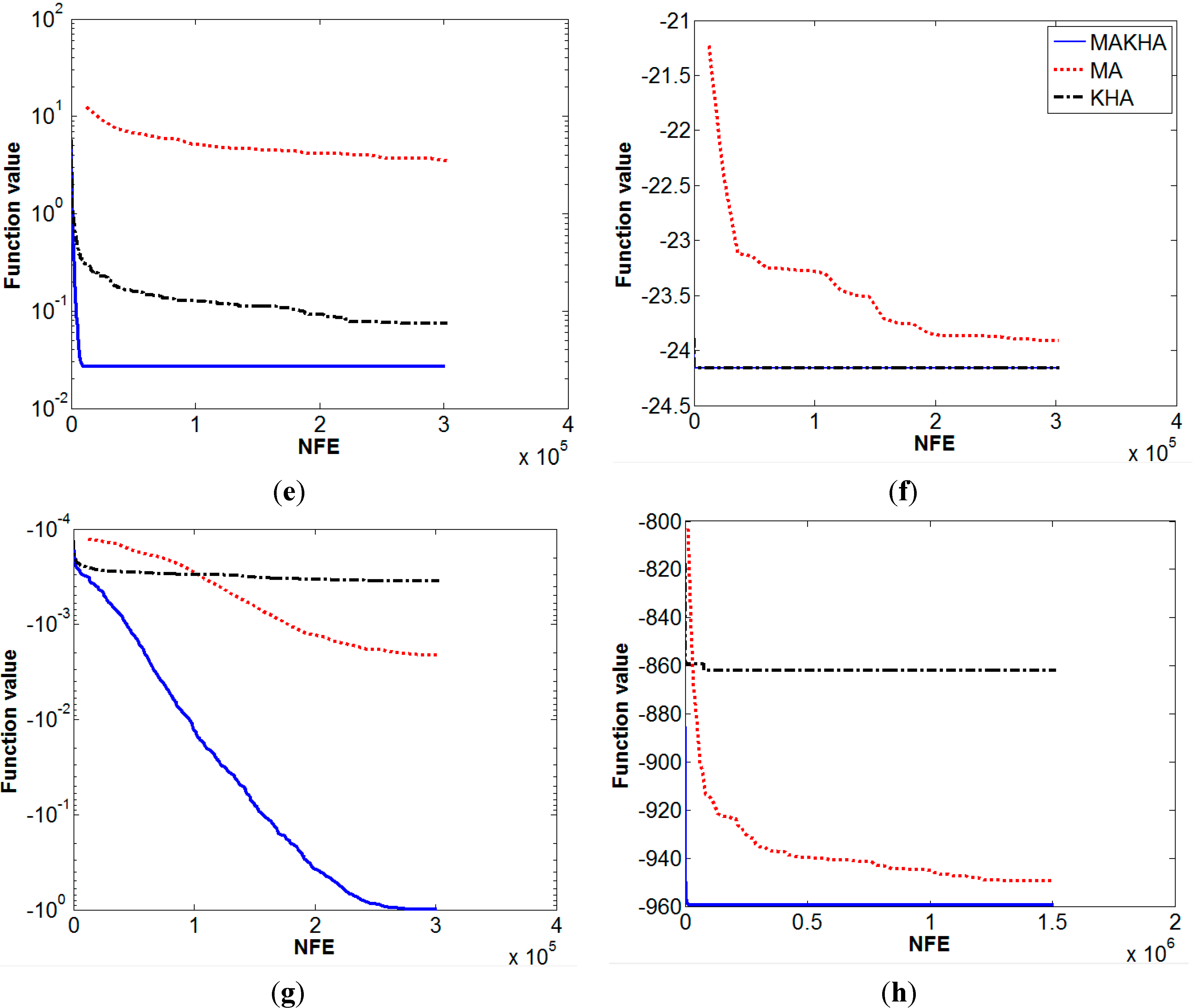


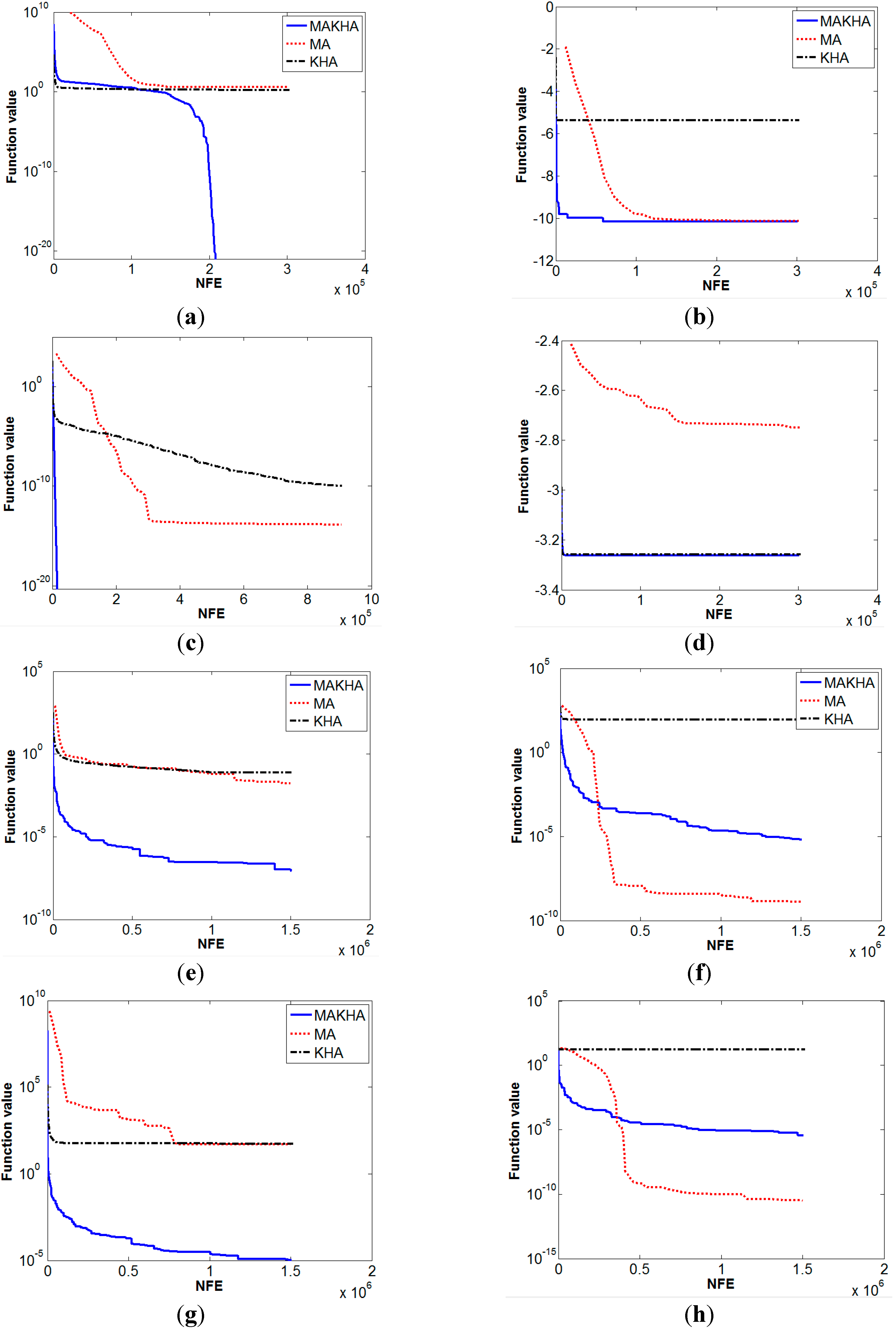

| Numerical Performance of | ||||||
|---|---|---|---|---|---|---|
| MA | KHA | MAKHA | ||||
| Objective function | fcalc | σ | fcalc | σ | fcalc | σ |
| Ackley | 4.8E−8 | 0 | 0.00129 | 0 | 0 | 0 |
| Beale | 0.084 | 0.125 | 0.0508 | 0.193 | 0 | 0 |
| Bird | −105.326 | 1.45 | −103.52 | 7.4 | −106.7645 | 0 |
| Booth | 0.179 | 0.172 | 1.28E−12 | 0 | 0 | 0 |
| Bukin 6 | 3.487 | 1.77 | 0.074 | 0.029 | 0.0267 | 0.0157 |
| Carrom table | −23.9138 | 0.436 | −24.1568 | 0 | −24.1568 | 0 |
| Cross-leg table | −0.002 | 4E−3 | −0.00035 | 0 | −0.9985 | 0 |
| Generalized egg holder | −949.58 | 0 | −862.1 | 0 | −959.641 | 0 |
| Goldstein-Price | 3.051 | 0.055 | 3 | 0 | 3 | 0 |
| Himmelblau | 0.179 | 0.187 | 7.4E−13 | 0 | 3.7E−31 | 0 |
| Levy 13 | 0.0616 | 0.08 | 2.1E−7 | 0 | 1.35E−31 | 0 |
| Schaffer | 0 | 0 | 1.7E−6 | 0 | 0 | 0 |
| Zettl | −0.0037 | 1E−3 | −0.00379 | 0 | −0.00379 | 0 |
| Helical valley | 136 | 250 | 9.8E−5 | 3E−3 | 0 | 0 |
| Powell | 18.46 | 49 | 1.9E−5 | 0 | 0 | 0 |
| Wood | 113.6 | 256 | 0.698 | 1.6 | 0 | 0 |
| Extended Cube | 3.568 | 0.8 | 1.658 | 5.28 | 0 | 0 |
| Shekel 5 | −10.139 | 0.06 | −5.384 | 3.1 | −10.1532 | 0 |
| Sphere | 1.4E−14 | 0 | 1E−10 | 0 | 0 | 0 |
| Hartman 6 | −2.7499 | 0.2 | −3.2587 | 0.06 | −3.2627 | 0.06 |
| Griewank | 0.0165 | 0.032 | 0.0769 | 0.095 | 8.4E−8 | 0 |
| Rastrigin | 1.3E-9 | 0 | 89.38 | 48.38 | 6.47E−6 | 0 |
| Rosenbrock | 47.45 | 7.5 | 52.593 | 18.97 | 1E−5 | 0 |
| Sine envelope sine wave | 3.3E−11 | 0 | 16.107 | 5.94 | 3.46E−6 | 0 |
| Styblinski-Tang | −1916.84 | 28.1 | −1645.42 | 36.9 | −1958.31 | 0 |
| Trigonometric | 1.35E−5 | 0 | 285.43 | 545.5 | 0 | 0 |
| Zacharov | 1.46E−10 | 0 | 1E−3 | 5.5E−3 | 8.4E−6 | 0 |

- (a)
- Exploration or diversification feature: The watch-jump process (MA), physical random diffusion (KHA), the somersault process (MA), and genetic operators (KHA).
- (b)
- Exploitation or intensification feature: The climb process (MA), the watch-jump process (MA), the induced motion (KHA), and the foraging activity (KHA).
7. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| A | Hartman’s recommended constants |
| a | Pseudo-gradient monkey step |
| b | Eyesight of the monkey (hybrid), which indicates the maximum distance the monkey (hybrid) can watch. |
| C | Shekel’s recommended constants |
| Cfood | Food coefficient |
| Cr | Crossover probability |
| Ct | Empirical and experimental Constants (Time constant) |
| c | Somersault interval |
| Di | Physical diffusion of krill (hybrid) number i |
| Dmax | Maximum diffusion speed |
| d | Somersault interval |
| dsi | Sensing distance of the krill |
| dsij | Distance between each 2 krill positions |
| f | Objective function |
| Fi | Foraging motion |
| G | Global minimum |
| H | Fitness value of the hybrid in MAKHA |
| I, i, j and l | Counters for any value |
| K | Fitness value of the krill in KHA |
| M | Number of local minima in Shekel function |
| LB | Lower boundaries and low limit of decision variable |
| Mu | Mutation probability |
| m | Dimension of the problem, i.e., number of variables. |
| N | Induced speed for KHA |
| Nc | Number of climb cycles |
| Nmax | Maximum induced speed |
| NP | Population size (number of points) |
| NV | Dimension of the problem, i.e., number of variables. |
| n | A counter |
| np | Number of problems |
| ns | Number of solvers |
| O | Hartman’s recommended constants |
| P | Pivot value |
| R | The half range of boundaries between the lower boundary and the upper boundary of the decision variables (X) |
| rps | The performance ratio |
| T | Time taken by krill or hybrid |
| tps | Performance metric |
| UB | Upper boundaries and high limit of decision variable |
| Vf | Foraging speed |
| wf or wN | Inertia weight |
| X | Decision variable matrix |
| Xfood | Centre of food density |
| x | Decision variable |
| Y | Decision variable matrix |
Greek Letters
| α | Somersault interval random output. |
| β | Shekel’s recommended constant |
| βfood | Food attractive factor |
| δ | Random direction vector |
| ∆t | Incremental period of time |
| ε | Small positive number to avoid singularity |
| ζζ | The simulating value of rps |
| ζmax | The maximum assumed value of rps |
| ρ | The cumulative probabilistic function of rps and the fraction of the total number of problems |
| σ | Standard deviation |
| ςς | The counter of ρ points |
References
- Floudas, C.A.; Gounaris, C.E. A review of recent advances in global optimization. J. Glob. Optim. 2009, 45, 3–38. [Google Scholar] [CrossRef]
- Zhao, R.; Tang, W. Monkey algorithm for global numerical optimization. J. Uncertain Syst. 2008, 2, 165–176. [Google Scholar]
- Gandomi, A.H.; Alavi, A.H. Krill herd: A new bio-inspired optimization algorithm. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 4831–4845. [Google Scholar] [CrossRef]
- Ituarte-Villarreal, C.M.; Lopez, N.; Espiritu, J.F. Using the Monkey Algorithm for Hybrid Power Systems Optimization. Procedia Comput. Sci. 2012, 12, 344–349. [Google Scholar] [CrossRef]
- Aghababaei, M.; Farsangi, M.M. Coordinated Control of Low Frequency Oscillations Using Improved Monkey Algorithm. Int. J. Tech. Phys. Probl. Eng. 2012, 4, 13–17. [Google Scholar]
- Yi, T.-H.; Li, H.-N.; Zhang, X.-D. A modified monkey algorithm for optimal sensor placement in structural health monitoring. Smart Mater. Struct. 2012, 21. [Google Scholar] [CrossRef]
- Yi, T.-H.; Li, H.-N.; Zhang, X.-D. Sensor placement on Canton Tower for health monitoring using asynchronous-climb monkey algorithm. Smart Mater. Struct. 2012, 21. [Google Scholar] [CrossRef]
- Yi, T.H.; Zhang, X.D.; Li, H.N. Modified monkey algorithm and its application to the optimal sensor placement. Appl. Mech. Mater. 2012, 178, 2699–2702. [Google Scholar] [CrossRef]
- Sur, C.; Shukla, A. Discrete Krill Herd Algorithm—A Bio-Inspired Meta-Heuristics for Graph Based Network Route Optimization. In Distributed Computing and Internet Technology; Springer: New York, NY, USA, 2014; pp. 152–163. [Google Scholar]
- Mandal, B.; Roy, P.K.; Mandal, S. Economic load dispatch using krill herd algorithm. Int. J. Electr. Power Energy Syst. 2014, 57, 1–10. [Google Scholar] [CrossRef]
- Zheng, L. An improved monkey algorithm with dynamic adaptation. Appl. Math. Comput. 2013, 222, 645–657. [Google Scholar] [CrossRef]
- Saremi, S.; Mirjalili, S.M.; Mirjalili, S. Chaotic krill herd optimization algorithm. Procedia Technol. 2014, 12, 180–185. [Google Scholar] [CrossRef]
- Wang, G.-G.; Gandomi, A.H.; Alavi, A.H. A chaotic particle-swarm krill herd algorithm for global numerical optimization. Kybernetes 2013, 42, 962–978. [Google Scholar] [CrossRef]
- Gharavian, L.; Yaghoobi, M.; Keshavarzian, P. Combination of krill herd algorithm with chaos theory in global optimization problems. In Proceedings of the 2013 3rd Joint Conference of AI & Robotics and 5th RoboCup Iran Open International Symposium (RIOS), Tehran, Iran, 8 April 2013; IEEE: Piscataway, NJ, USA, 2013. [Google Scholar]
- Wang, J.; Yu, Y.; Zeng, Y.; Luan, W. Discrete monkey algorithm and its application in transmission network expansion planning. In Proceedings of the Power and Energy Society General Meeting, Minneapolis, MN, USA, 25–29 July 2010; IEEE: Piscataway, NJ, USA, 2010. [Google Scholar]
- Wang, G.; Guo, L.; Gandomi, A.H.; Cao, L. Lévy-flight krill herd algorithm. Math. Probl. Eng. 2013. [Google Scholar] [CrossRef]
- Guo, L.; Wang, G.-G.; Gandomi, A.H.; Alavi, A.H.; Duan, H. A new improved krill herd algorithm for global numerical optimization. Neurocomputing 2014, 138, 392–402. [Google Scholar] [CrossRef]
- Wang, G.; Guo, L.; Wang, H.; Duan, H.; Liu, L.; Li, J. Incorporating mutation scheme into krill herd algorithm for global numerical optimization. Neural Comput. Appl. 2014, 24, 853–871. [Google Scholar] [CrossRef]
- Wang, G.-G.; Guo, L.H.; Gandomi, A.H.; Alavi, A.H.; Duan, H. Simulated annealing-based krill herd algorithm for global optimization. In Abstract and Applied Analysis; Hindawi Publishing Corporation: Cairo, Egypt, 2013. [Google Scholar]
- Blum, C.; Roli, A. Metaheuristics in combinatorial optimization: Overview and conceptual comparison. ACM Comput. Surv. 2003, 35, 268–308. [Google Scholar] [CrossRef]
- Lozano, M.; García-Martínez, C. Hybrid metaheuristics with evolutionary algorithms specializing in intensification and diversification: Overview and progress report. Comput. Op. Res. 2010, 37, 481–497. [Google Scholar] [CrossRef]
- Liu, P.-F.; Xu, P.; Han, S.-X.; Zheng, J.-Y. Optimal design of pressure vessel using an improved genetic algorithm. J. Zhejiang Univ. Sci. A 2008, 9, 1264–1269. [Google Scholar] [CrossRef]
- Abdullah, A.; Deris, S.; Mohamad, M.S.; Hashim, S.Z.M. A New Hybrid Firefly Algorithm for Complex and Nonlinear Problem. In Distributed Computing and Artificial Intelligence; Omatu, S., Bersini, H., Corchado, J.M., Rodríguez, S., Pawlewski, P., Bucciarelli, E., Eds.; Springer: Berlin, Germany; Heidelberg, Germany, 2012; pp. 673–680. [Google Scholar]
- Biswas, A.; Dasgupta, S.; Das, S.; Abraham, A. Synergy of PSO and Bacterial Foraging Optimization—A Comparative Study on Numerical Benchmarks Innovations in Hybrid Intelligent Systems; Corchado, E., Corchado, J., Abraham, A., Eds.; Springer: Berlin, Germany; Heidelberg, Germany, 2007; pp. 255–263. [Google Scholar]
- Li, S.; Chen, H.; Tang, Z. Study of Pseudo-Parallel Genetic Algorithm with Ant Colony Optimization to Solve the TSP. Int. J. Comput. Sci. Netw. Secur. 2011, 11, 73–79. [Google Scholar]
- Nguyen, K.; Nguyen, P.; Tran, N. A hybrid algorithm of Harmony Search and Bees Algorithm for a University Course Timetabling Problem. Int. J. Comput. Sci. Issues 2012, 9, 12–17. [Google Scholar]
- Farahani, Sh.M.; Abshouri, A.A.; Nasiri, B.; Meybodi, M.R. Some hybrid models to improve Firefly algorithm performance. Int. J. Artif. Intell. 2012, 8, 97–117. [Google Scholar]
- Kim, D.H.; Abraham, A.; Cho, J.H. A hybrid genetic algorithm and bacterial foraging approach for global optimization. Inf. Sci. 2007, 177, 3918–3937. [Google Scholar] [CrossRef]
- Kim, D.H.; Cho, J.H. A Biologically Inspired Intelligent PID Controller Tuning for AVR Systems. Int. J. Control Autom. Syst. 2006, 4, 624–636. [Google Scholar] [CrossRef]
- Dehbari, S.; Rosta, A.P.; Nezhad, S.E.; Tavakkoli-Moghaddam, R. A new supply chain management method with one-way time window: A hybrid PSO-SA approach. Int. J. Ind. Eng. Comput. 2012, 3, 241–252. [Google Scholar] [CrossRef]
- Zahrani, M.S.; Loomes, M.J.; Malcolm, J.A.; Dayem Ullah, A.Z.M.; Steinhöfel, K.; Albrecht, A.A. Genetic local search for multicast routing with pre-processing by logarithmic simulated annealing. Comput. Op. Res. 2008, 35, 2049–2070. [Google Scholar] [CrossRef]
- Huang, K.-L.; Liao, C.-J. Ant colony optimization combined with taboo search for the job shop scheduling problem. Comput. Oper. Res. 2008, 35, 1030–1046. [Google Scholar] [CrossRef]
- Shahrouzi, M. A new hybrid genetic and swarm optimization for earthquake accelerogram scaling. Int. J. Optim. Civ. Eng. 2011, 1, 127–140. [Google Scholar]
- Bäck, T.; Schwefel, H.-P. An overview of evolutionary algorithms for parameter optimization. Evolut. Comput. 1993, 1, 1–23. [Google Scholar] [CrossRef]
- Jamil, M.; Yang, X.-S. A literature survey of benchmark functions for global optimization problems. Int. J. Math. Model. Numer. Optim. 2013, 4, 150–194. [Google Scholar]
- Mishra, S.K. Global optimization by differential evolution and particle swarm methods: Evaluation on some benchmark functions, Social Science Research Network, Rochester, NY, USA. Available online: http://ssrn.com/abstract=933827 (accessed on 3 April 2015).
- Mishra, S.K. Some new test functions for global optimization and performance of repulsive particle swarm method, Social Science Research Network, Rochester, NY, USA. Available online: http://ssrn.com/abstract=926132 (accessed on 3 April 2015).
- Goldstein, A.; Price, J. On descent from local minima. Math. Comput. 1971, 25, 569–574. [Google Scholar] [CrossRef]
- Himmelblau, D.M. Applied Nonlinear Programming; McGraw-Hill Companies: New York, NY, USA, 1972. [Google Scholar]
- Ortiz, G.A. Evolution Strategies (ES); Mathworks: Natick, MA, USA, 2012. [Google Scholar]
- Schwefel, H.-P.P. Evolution and Optimum Seeking: The Sixth Generation; John Wiley & Sons: Hoboken, NJ, USA, 1993. [Google Scholar]
- Fletcher, R.; Powell, M.J. A rapidly convergent descent method for minimization. Comput. J. 1963, 6, 163–168. [Google Scholar] [CrossRef]
- Fu, M.C.; Hu, J.; Marcus, S.I. Model-based randomized methods for global optimization. In Proceedings of the 17th International Symposium on Mathematical Theory of Networks and Systems, Kyoto, Japan, 24–28 July 2006.
- Grippo, L.; Lampariello, F.; Lucidi, S. A truncated Newton method with nonmonotone line search for unconstrained optimization. J. Optim. Theory Appl. 1989, 60, 401–419. [Google Scholar] [CrossRef]
- Oldenhuis, R.P.S. Extended Cube Function; Mathworks: Natick, MA, USA, 2009. [Google Scholar]
- Pintér, J. Global Optimization in Action: Continuous and Lipschitz optimization: Algorithms, Implementations and Applications; Springer Science & Business Media: Berlin, Germany; Heidelberg, Germany, 1995; Volume 6. [Google Scholar]
- Schumer, M.; Steiglitz, K. Adaptive step size random search. Autom. Control IEEE Trans. 1968, 13, 270–276. [Google Scholar] [CrossRef]
- Hartman, J.K. Some experiments in global optimization. Nav. Res. Logist. Q. 1973, 20, 569–576. [Google Scholar] [CrossRef]
- Griewank, A.O. Generalized descent for global optimization. J. Optim. Theory Appl. 1981, 34, 11–39. [Google Scholar] [CrossRef]
- Rastrigin, L. Systems of Extremal Control; Nauka: Moscow, Russia, 1974. [Google Scholar]
- Rosenbrock, H.H. An automatic method for finding the greatest or least value of a function. Comput. J. 1960, 3, 175–184. [Google Scholar] [CrossRef]
- Silagadze, Z. Finding two-dimensional peaks. Phys. Part. Nucl. Lett. 2007, 4, 73–80. [Google Scholar] [CrossRef]
- Dixon, L.C.W.; Szegö, G.P. (Eds.) Towards Global Optimisation 2; North-Holland Publishing: Amsterdam, The Netherlands, 1978.
- Rahnamayan, S.; Tizhoosh, H.R.; Salama, M.M. A novel population initialization method for accelerating evolutionary algorithms. Comput. Math. Appl. 2007, 53, 1605–1614. [Google Scholar] [CrossRef]
- Dolan, E.D.; Moré, J.J. Benchmarking optimization software with performance profiles. Math. Program. 2002, 91, 201–213. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khalil, A.M.E.; Fateen, S.-E.K.; Bonilla-Petriciolet, A. MAKHA—A New Hybrid Swarm Intelligence Global Optimization Algorithm. Algorithms 2015, 8, 336-365. https://0-doi-org.brum.beds.ac.uk/10.3390/a8020336
Khalil AME, Fateen S-EK, Bonilla-Petriciolet A. MAKHA—A New Hybrid Swarm Intelligence Global Optimization Algorithm. Algorithms. 2015; 8(2):336-365. https://0-doi-org.brum.beds.ac.uk/10.3390/a8020336
Chicago/Turabian StyleKhalil, Ahmed M.E., Seif-Eddeen K. Fateen, and Adrián Bonilla-Petriciolet. 2015. "MAKHA—A New Hybrid Swarm Intelligence Global Optimization Algorithm" Algorithms 8, no. 2: 336-365. https://0-doi-org.brum.beds.ac.uk/10.3390/a8020336





