Target Detection Algorithm Based on Two Layers Human Visual System
Abstract
:1. Introduction
2. Algorithm Based on Human Visual System
2.1. Framework of the Proposed Two Stage Algorithm—A Brief Description
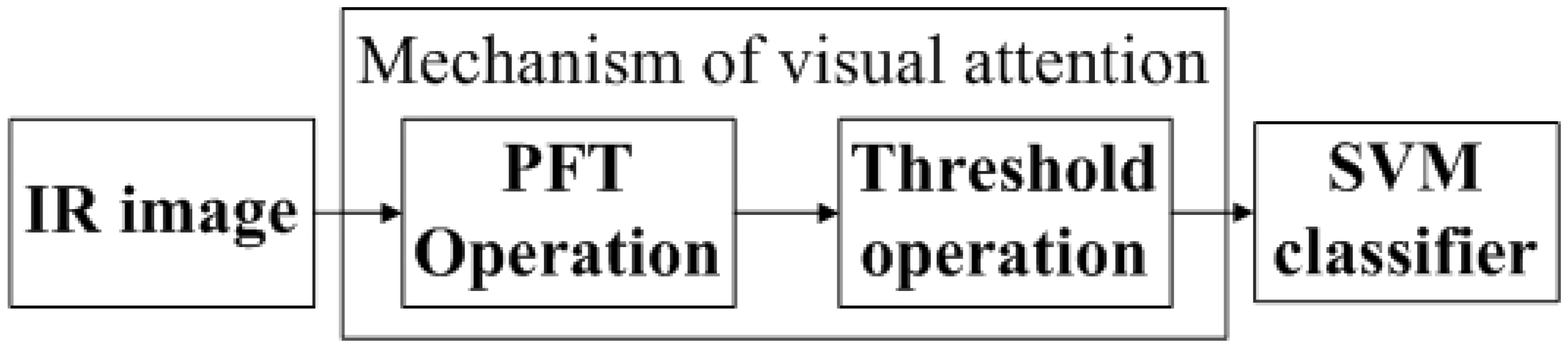
2.2. The Theory of Frequency-Domain in the First Stage
2.3. The Theory of SVM Classifier in the Second Stage
3. Experimental Section

3.1. Experiment Result of One Layer




3.2. Experiment Result of Two Layers


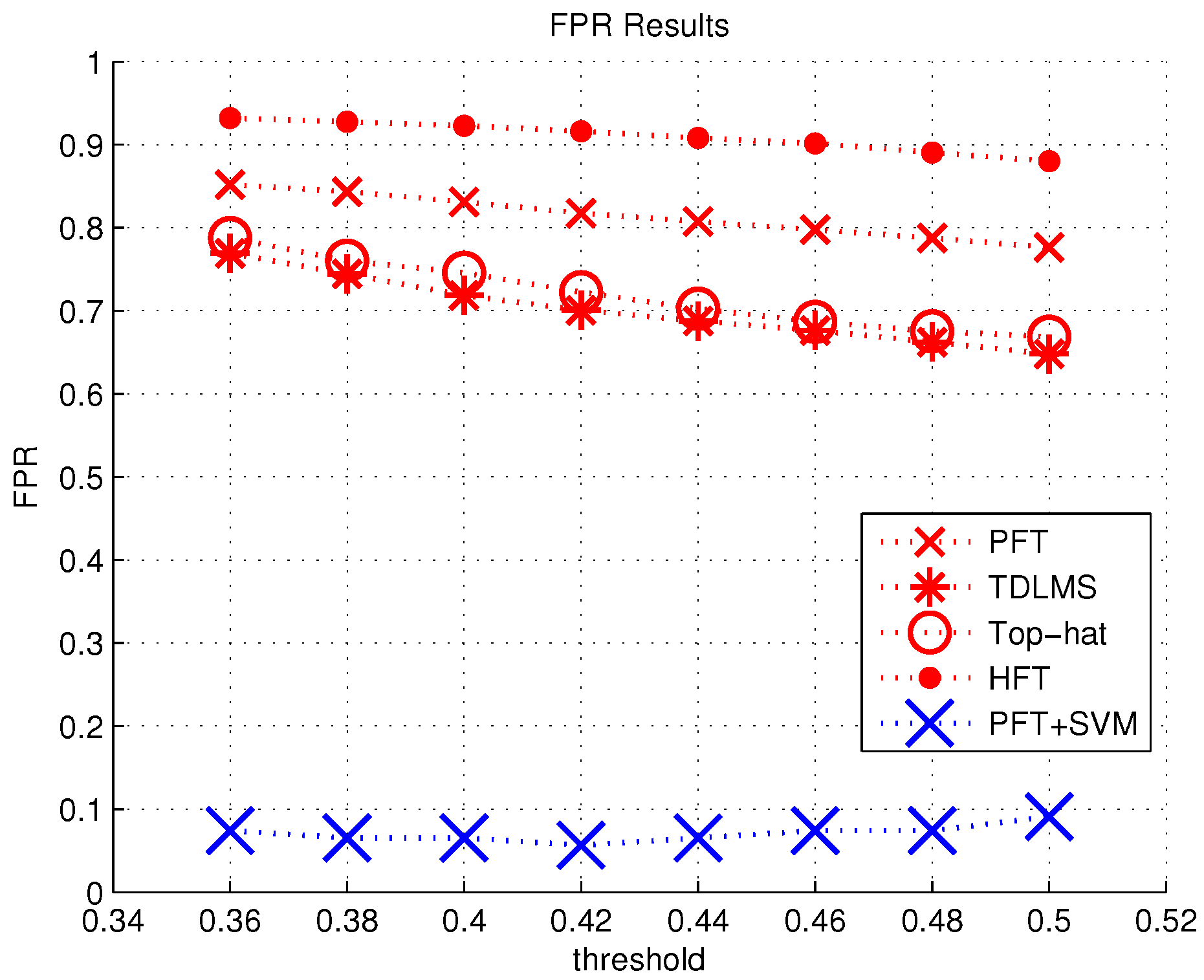
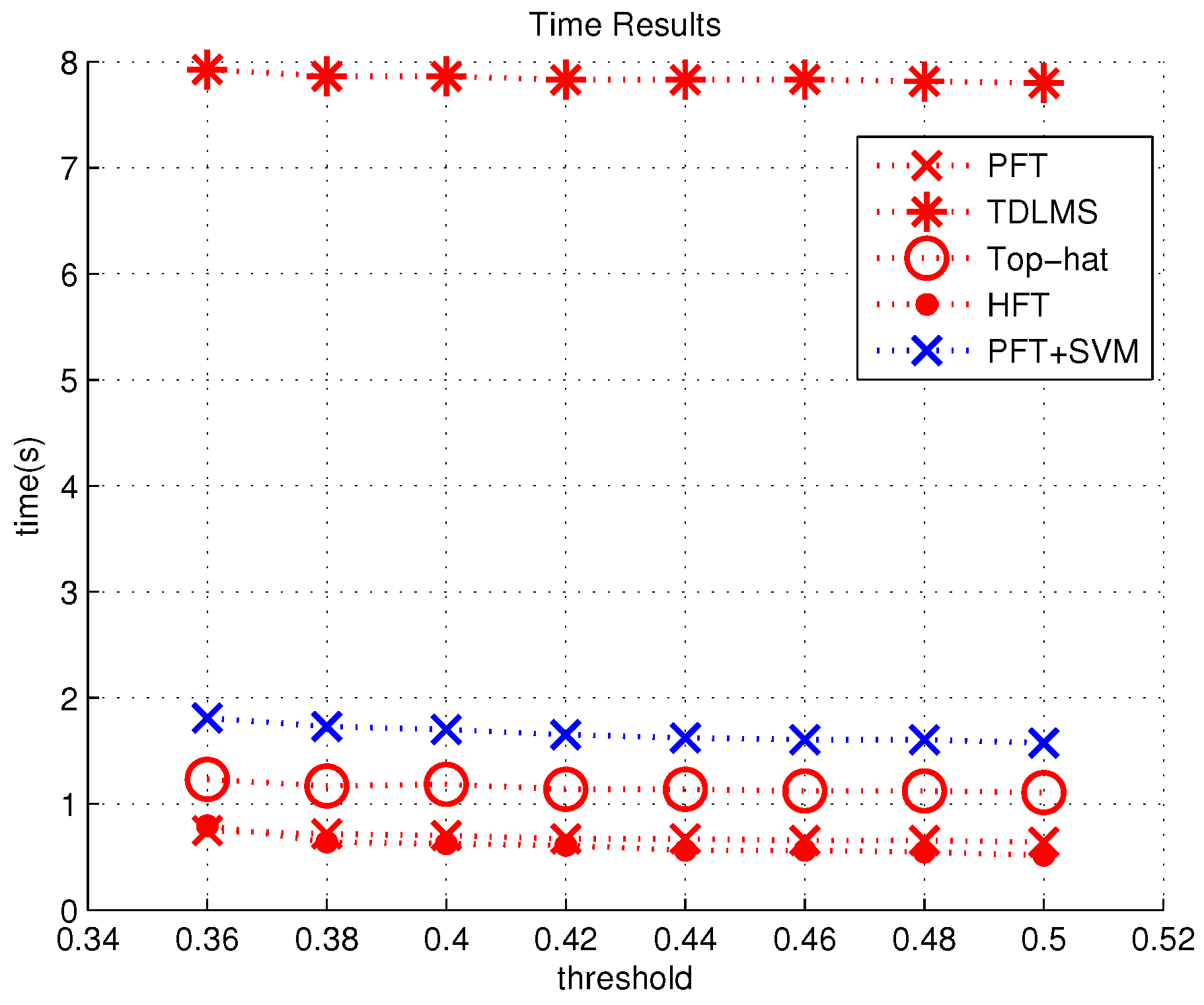
| Method | TPR | FPR | Time(s) |
|---|---|---|---|
| two layers (PFT + SVM) | 0.94 | 0.0654 | 1.623 |
| one layer (PFT) | 0.94 | 0.8073 | 0.671 |
| one layer (TOP-HAT) | 0.89 | 0.7024 | 1.139 |
| one layer (TDLMS) | 0.75 | 0.6875 | 7.831 |
| one layer (HFT) | 0.29 | 0.9081 | 0.562 |
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- GUO, W.; Sun, J.; Lin, H. Dynamic template preparing and application on FLIR target recognition. In Proceedings of the IEEE International Conference on Electrical and Control Engineering (ICECE), Wuhan, China, 25–27 June 2010; pp. 864–867.
- Tom, V.T.; Peli, T.; Leung, M.; Bondaryk, J.E. Morphology-based algorithm for point target detection in infrared backgrounds. Pro. SPIE 1993, 1954. [Google Scholar] [CrossRef]
- Deshpande, S.D.; Meng, H.E.; Venkateswarlu, R.; Chan, P. Max-mean and max-median filters for detection of small targets. In Proceedings of the SPIE’s International Symposium on Optical Science, Engineering, and Instrumentation, Denver, CO, USA, 18–23 July 1999; pp. 74–83.
- Wang, P.; Tian, J.; Gao, C.Q. Infrared small target detection using directional highpass filters based on LS-SVM. Electron. Lett. 2009, 45, 156–158. [Google Scholar] [CrossRef]
- Hou, X.; Zhang, L. Saliency detection: A spectral residual approach. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8.
- Guo, C.; Ma, Q.; Zhang, L. Spatio-temporal saliency detection using phase spectrum of quaternion fourier transform. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008; pp. 1–8.
- Li, J.; Levine, M.D.; An, X.; Xu, X.; He, H. Visual saliency based on scale-space analysis in the frequency domain. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 996–1010. [Google Scholar] [CrossRef] [PubMed]
- Gao, C.; Meng, D.; Yang, Y.; Wang, Y.; Zhou, X.; Hauptmann, A.G. Infrared patch-image model for small target detection in a single image. IEEE Trans. Image Process. 2013, 22, 4996–5009. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Shi, D.; Yang, W. Infared target extraction in FLIR imagery based on spatio temporal using fuzzy clustering. In Proceedings of the Second International Symposium on Intelligent Information Technology Application, Shanghai, China, 20–22 December 2008; Volume 1, pp. 848–851.
- Zheng, S.; Liu, J.; Tian, J.W. An SVM-based small target segmentation and clustering approach. In Proceedings of the International Conference on Machine Learning and Cybernetics, Shanghai, China, 26–29 August 2004; Volume 6, pp. 3318–3323.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, Z.; Yang, J.; Jiang, S.; Wei, C. Target Detection Algorithm Based on Two Layers Human Visual System. Algorithms 2015, 8, 541-551. https://0-doi-org.brum.beds.ac.uk/10.3390/a8030541
Cui Z, Yang J, Jiang S, Wei C. Target Detection Algorithm Based on Two Layers Human Visual System. Algorithms. 2015; 8(3):541-551. https://0-doi-org.brum.beds.ac.uk/10.3390/a8030541
Chicago/Turabian StyleCui, Zheng, Jingli Yang, Shouda Jiang, and Changan Wei. 2015. "Target Detection Algorithm Based on Two Layers Human Visual System" Algorithms 8, no. 3: 541-551. https://0-doi-org.brum.beds.ac.uk/10.3390/a8030541





