1. Introduction
Solving nonlinear equations by iterative methods have been of great interest to numerical analysts. The most famous one-point iterative method is probably Newton’s Equation [
1]:
which converges quadratically. However, the condition
in a neighborhood of the required root is severe indeed for convergence of Newton method, which restricts its applications in practical. For resolving this problem, Wu in [
2] proposed the following one-point iterative method
where
and
λ is chosen such that the corresponding function values
and
have the same signs. This method converges quadratically under the condition
while
in some points is permitted. Wang and Zhang in [
3] obtained the error equation of the Equation (
1) as follows
where
and
a is the root of the nonlinear equation
The convergence order and computational efficiency of the one-point iterative methods are lower than multipoint iterative methods. Multipoint iterative methods can overcome theoretical limits of one-point methods concerning the convergence order and computational efficiency. In recent years, many multipoint iterative methods have been proposed for solving nonlinear equations, see [
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18]. Wang and Liu in [
4] developed the following eighth-order iterative method without memory by Hermite interpolation methods
where
Using the same strategy, Kou in [
5] presented a family of eighth-order iterative method without memory. The Equation (
3) is a special case of the Kou’s method. Petković in [
6] claimed a general class of optimal
n-point methods without memory by Hermite interpolation methods, which have the order of convergence
and require evaluations of
n functions and one first-order derivative. The Equation (
3) is a special case of the Petković’s
n-point Method for
But, the Petković’s
n-point method gives no specific iterative scheme and error relation for
In this paper, we construct a class of
n-point iterative methods with and without memory by Hermite interpolation methods and give the specific iterative scheme and error relation for all
This paper is organized as follows. In
Section 2, based on Wu’s Equation [
2] and Petković’s
n-point Equation [
6], we derive a family of
n-point iterative methods without memory for solving nonlinear equations. We prove that the order of convergence of the
n-point methods without memory is
requiring the evaluations of
n functions and one first-order derivative in per full iteration. Kung and Traub in [
7] conjectured that a multipoint iteration without memory based on
n functional evaluations could achieve an optimal convergence of order
. The new methods without memory agree with the conjecture. Further accelerations of convergence speed are attained in
Section 3. A family of
n-point iterative methods with memory is obtained by using a self-accelerating parameter in per full iteration. This self-accelerating parameter is calculated using information available from the current and previous iterations. Numerical examples are given in
Section 4 to confirm theoretical results.
2. The Optimal Fourth-, Eighth- and th Order Iterative Methods
Based on Wu’s Equation [
2] and Petković’s
n-point methods [
6], we derive a general optimal
th order family and write it in the following form:
where
is a constant and
k being the iteration index. The entries
are approximations with the associated error
Using the Taylor series and symbolic computation in the programming package Mathematica, we can find the order of convergence and the asymptotic error constant (AEC) of the
n-point methods Equation (
4) for
and
, respectively. For simplicity, we sometimes omit the iteration index
n and write
e instead of
. The approximation
to the root
a will be denoted by
. Regarding Equation (
4), let us define
The following abbreviations are used in the program.
Program (written in Mathematica)
fx=fla*(e+c2*e^2+c3*e^3+c4*e^4+c5*e^5+c6*e^6+c7*e^7+c8*e^8);
dfx=D[fx,e];
t=Series[fx/(L*fx+dfx),{e,0,8}];
d=Series[e-t,{e,0,8}]//Simplify
fy=Series[fla*(d+c2*d^2+c3*d^3+c4*d^4),{e,0,8}];
fxy=Series[(fy-fx)/(d-e),{e,0,8}];
z=Series[d-fy/(2*fxy-dfx),{e,0,8}]//Simplify
fz=Series[fla*(z+c2*z^2),{e,0,8}];
fyz=Series[(fy-fz)/(d-z),{e,0,8}];
fxz=Series[(fx-fz)/(e-z),{e,0,8}];
fxxy=Series[(dfx-fxy)/(e-d),{e,0,8}];
fzxx=Series[(dfx-fxz)/(e-z),{e,0,8}];
fzxxy=Series[(fzxx-fxxy)/(z-d),{e,0,8}];
fzxy=Series[(fxz-fyz)/(e-d),{e,0,8}];
e1=Series[z-fz/(fyz+fzxy*(z-d)+fzxxy*(z-e)*(z-d)),{e,0,8}]//Simplify
We obtain the asymptotic error constants of
n-point methods Equation (
4) with
. Altogether, we can state the following theorem.
Theorem 1. Let
I be an open interval and
a simple zero point of a sufficiently differentiable function
. Then the new method defined by Equation (
4)
is fourth order, and satisfies the error equation
the Equation (
4) (
) is eighth-order and satisfies the error equation
where
The order of the convergence of the Equation (
4) is analyzed in the following theorem.
Theorem 2. Let
I be an open interval and
a simple zero point of a sufficiently differentiable function
. Then the
n-point family Equation (
4) converges with at least
th order and satisfies the error relation
where
and
Proof. We prove the theorem by induction. For
the theorem is valid by Theorem 1. Let us assume that Equation (
10) is true for the intermediate error relations, then the intermediate error relations are of the form
where
Using Equation (
4) and Equation (11) and noting that
, we have
Hence, by induction, we conclude that the error relations can be written in the following form
3. New Families of Iterative Methods with Memory
In this section we will improve the convergence order of the family Equation (
4). We observe from Equation (
13) that the order of convergence of the family Equation (
4) is
when
With the choice
, it can be proved that the order of the family Equation (
4) would exceed
. However, the exact values of
and
are not available in practice and such acceleration of convergence can not be realized. But we could approximate the parameter
λ by
. The parameter
can be computed by using information available from the current and previous iterations and satisfies
such that the
th order asymptotic convergence constant to be zero in Equation (
13). We consider the following three methods for
:
where
and
where
and
where
and
The parameter
is recursively calculated as the iteration proceeds using Equation (
14)–Equation (16) in Equation (
4). Substituting
instead of
λ in Equation (
4), we can obtain the following iterative method with memory
where
and the parameter
is calculated by using one of the Equations (
14)– (16) and depends on the data available from the current and the previous iterations.
Lemma 1. Let
be the Hermite interpolating polynomial of the degree
m that interpolates a function
f at
m distinct interpolation nodes
contained in an interval
Iand the derivative
is continuous in
I and the Hermite interpolating polynomial
satisfied the condition
. Define the errors
and assume that
all nodes are sufficiently close to the zero a;
the condition holds.
Proof. The error of the Hermite interpolation can be expressed as follows
Differentiating Equation (
20) at the point
, we obtain
Taylor’s series of derivatives of
fat the point
and
about the zero
a of
fgive
where
Substituting Equation (
24) and Equation (
25) into Equation (
22), we have
and
The concept of the
R-order of convergence [
1] and the following assertion (see [
8]) will be applied to estimate the convergence order of the iterative method with memory Equation (
17). Now we can state the following convergence theorem for iterative method with memory Equation (
17).
Theorem 3. Let the varying parameter
in the iterative Equation (
17) be calculated by Equation (14). If an initial approximation
is sufficiently close to a simple zero
a of
, then the
R-order of convergence of the
n-point Equation (
17) with memory is at least
for
and at least
for
Proof. First, let us consider the case
and assume that the iterative sequences
and
have the
R-order
, respectively, we have
where
tends to the asymptotic error constant
when
From Equation (
13), we obtain the following error relations
Using the Lemma 1 for
, we obtain
Substituting Equation (
32) into Equation (
30) and Equation (
31) instead of
λ, we have
By comparing exponents of
appearing in two pairs of relations Equation (
29)–Equation (
33) and Equation (
28)–Equation (
34), we get the following system of equations
The solution of the system Equation (
35) is given by
and
. Therefore, the
R-order of the methods with memory Equation (
17) is at least
for
. For example, the R-order of the three-point family Equation (
17) is at least 9, the four-point family has the R-order at least 18, assuming that
is calculated by Equation (
14).
The case
differs from the previous analysis; Hermit’s interpolating polynomial is constructed at the nodes
. Substituting Equation (
32) into Equation (
2) and Equation (
8) instead of
λ, we have
By comparing exponents of
appearing in two pairs of relations Equation (
29)–Equation (
36) and Equation (
28)–Equation (
37), we get the following system of equations
Positive solution of the system Equation (
38) is given by
and
. Therefore, the
R-order of the methods with memory Equation (
17) with Equation (
14) is at least
for
Theorem 4. Let the varying parameter
in the iterative Equation (
17) be calculated by Equation (
15). If an initial approximation
is sufficiently close to a simple zero
a of
, then the
R-order of convergence of the
n-point methods Equation (
17) with memory is at least
for
, at least
for
and at least
for
Proof. The proof is similar to the Theorem 3.
Theorem 5. Let the varying parameter
in the iterative Equation (
17) be calculated by Equation (
16). If an initial approximation
is sufficiently close to a simple zero
a of
, then the
R-order of convergence of the
n-point Equation (
17) with memory is at least
for
, at least
for
and at least
for
Proof. The proof is similar to the Theorem 3.
4. Numerical Results
Now, the new family Equation (
4) without memory and the corresponding family Equation (
17) with memory are employed to solve some nonlinear equations and compared with several known iterative methods. All algorithms are implemented using Symbolic Math Toolbox of MATLAB 7.0. For demonstration, we have selected three methods displayed below.
King’s methods without memory ( KM4, see [
9] ):
where
.
Bi-Wu-Ren method without memory ( BRM8, see [
10] ):
where
is a real-valued function satisfying the conditions
and
Petković-Ilić-Džunić method with memory ( PD, see [
12] )
where
The parameter
can be calculated by the following three formulas:
The absolute errors
in the first four iterations are given in
Table 1,
Table 2,
Table 3 and
Table 4, where
a is the exact root computed with 2400 significant digits. The computational order of convergence
ρ is defined by [
19]:
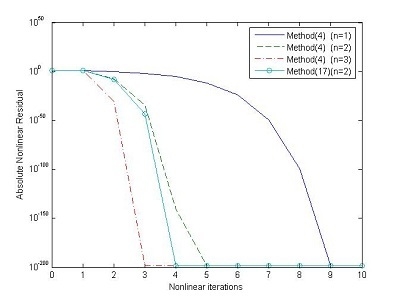
The iterative processes of the Equations (4) and (17) are given in
Figure 1, where Equation (4) (n=1) is one-point method. The parameters of the Equations (4) and (17) are
. The initial value is
. The stopping criterium is
. We will call
the nonlinear residual or residual. The
Figure 1 is a semilog plot of residual history, the norm of the nonlinear residual against the iteration number.
Following test functions are used:
Table 1.
Numerical results for by the methods without memory.
Table 1.
Numerical results for by the methods without memory.
| Methods | | | | ρ |
|---|
|
Equation (4) | 0.32719E−4 | 0.57076E−18 | 0.52848E−73 | 4.0000005 |
| Equation (4) | 0.58111E−4 | 0.71445E−17 | 0.16328E−68 | 3.9999938 |
| 0.24269E−3 | 0.13078E−13 | 0.11033E−54 | 3.9999864 |
| 0.40513E−6 | 0.32351E−48 | 0.53484E−385 | 8.0000001 |
| Equation (4) | 0.22673E−8 | 0.83510E−70 | 0.28282E−561 | 8.0000000 |
| Equation (4) | 0.18012E−9 | 0.75259E−83 | 0.69916E−670 | 8.0000000 |
Table 2.
Numerical results for by the methods without memory.
Table 2.
Numerical results for by the methods without memory.
| Methods | | | | ρ |
|---|
| Equation (4) | 0.29673E−2 | 0.37452E−10 | 0.94752E−42 | 4.0001713 |
| Equation (4) | 0.27276E−4 | 0.11867E−19 | 0.42516E−81 | 4.0000025 |
| 0.37189E−2 | 0.32631E−9 | 0.19533E−37 | 3.9993916 |
| 0.84179E−4 | 0.62964E−31 | 0.61512E−248 | 8.0000456 |
| Equation (4) | 0.34838E−7 | 0.19030E−62 | 0.15080E−504 | 8.0000000 |
| Equation (4) | 0.11873E−7 | 0.80149E−66 | 0.34562E−531 | 8.0000000 |
Table 3.
Numerical results for by the methods with memory.
Table 3.
Numerical results for by the methods with memory.
| Methods | | | | ρ |
|---|
| Equation (42) | 0.10690E−2 | 0.10554E−12 | 0.24668E−58 | 4.5605896 |
| Equation (43) | 0.10690E−2 | 0.58225E−14 | 0.18875E−67 | 4.7487424 |
| Equation (14) - (17) | 0.32719E−4 | 0.42649E−19 | 0.26035E−87 | 4.5827899 |
| Equation (15) - (17) | 0.32719E−4 | 0.47493E−20 | 0.16676E−96 | 4.8272294 |
| Equation (14) - (17) | 0.58111E−4 | 0.25364E−18 | 0.61743E−84 | 4.5691828 |
| Equation (15) - (17) | 0.58111E−4 | 0.28197E−19 | 0.69228E−93 | 4.8066915 |
| Equation (14) - (17) | 0.22673E−8 | 0.14247E−76 | 0.38886E−690 | 8.9963034 |
| Equation (15) - (17) | 0.22673E−8 | 0.53419E−81 | 0.96778E−777 | 9.5795515 |
| Equation (16) - (17) | 0.22673E−8 | 0.45910E−83 | 0.96092E−815 | 9.7957408 |
| Equation (14) - (17) | 0.18012E−9 | 0.49194E−86 | 0.27126E−775 | 9.0024260 |
| Equation (15) - (17) | 0.18012E−9 | 0.13193E−91 | 0.20518E−878 | 9.5794268 |
| Equation (16) - (17) | 0.18012E−9 | 0.11706E−93 | 0.17692E−918 | 9.7974669 |
Table 4.
Numerical results for by the methods with memory.
Table 4.
Numerical results for by the methods with memory.
| Methods | | | | ρ |
|---|
|
Equation (42) | 0.14930E−1 | 0.54292E−8 | 0.20342E−37 | 4.5697804 |
| Equation (43) | 0.14930E−1 | 0.32753E−9 | 0.16659E−45 | 4.7387964 |
| Equation (14) - (17) | 0.29673E−2 | 0.10381E−11 | 0.90169E−55 | 4.5538013 |
| Equation (15) - (17) | 0.29673E−2 | 0.13370E−13 | 0.29875E−67 | 4.7285160 |
| Equation (14) - (17) | 0.27276E−4 | 0.76276E−20 | 0.21310E−91 | 4.6005252 |
| Equation (15) - (17) | 0.27276E−4 | 0.62055E−21 | 0.70672E−102 | 4.8635157 |
| Equation (14) - (17) | 0.34838E−7 | 0.12841E−67 | 0.15487E−611 | 9.0002878 |
| Equation (15) - (17) | 0.34838E−7 | 0.34679E−73 | 0.10151E−705 | 9.5835521 |
| Equation (16) - (17) | 0.34838E−7 | 0.41211E−75 | 0.11560E−741 | 9.8127640 |
| Equation (14) - (17) | 0.11873E−7 | 0.35119E−73 | 0.13260E−661 | 8.9795793 |
| Equation (15) - (17) | 0.11873E−7 | 0.43166E−77 | 0.67183E−743 | 9.5883270 |
| Equation (16) - (17) | 0.11873E−7 | 0.45981E−83 | 0.29759E−820 | 9.7754885 |
Figure 1.
Iterative processes of different methods for the function
Figure 1.
Iterative processes of different methods for the function