A New Approach for Automatic Removal of Movement Artifacts in Near-Infrared Spectroscopy Time Series by Means of Acceleration Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Algorithm
| Parameter | Value | Description |
|---|---|---|
| q | 2 s | Defines the MSD window length 2q + 1 |
| wsize | 15 min | Moving window length for the Zack triangle algorithm |
| wstep | 5 min | Step size for the Zack triangle algorithm |
| Tarea | 0.005 | Noise criteria |
| Tareanorm | 0.2 | Normalized noise criteria |
| Lmin | 2 s | Minimum allowed artifact size or gap between artifacts |
| “condition free” | no default | Defines the fixed segments for the reconstruction (no artifacts) |
| p | 1 s | Window length for the FIR filter, Savitzky-Golay filter and MSD within the artifact removal procedure |
| fc,FIR | 0.5 Hz | Cut-off frequency of the FIR filter within the artifact removal procedure |

2.1.1. Movement Detection

2.1.2. Artifact Detection
2.1.3. Segmentation
2.1.4. Artifact Removal
2.1.5. Reconstruction
2.2. Validation
2.2.1. Measurements
2.2.2. NIRS Instrumentation
2.2.3. Validation of AMARA against Human Scorers, MARA and ABAMAR
| S1 | S2 | S3 | S4 | AMARA | MARA | ABAMAR | AMARAacc | |
|---|---|---|---|---|---|---|---|---|
| NMethod | 5553 | 5011 | 6998 | 7526 | 14,695 | 12,732 | 8478 | 11,334 |
| 58 ± 24 | 52 ± 22 | 73 ± 30 | 78 ± 28 | 153 ± 42 | 133 ± 60 | 88 ± 29 | 118 ± 35 | |
| L [s] | 101 ± 42 | 74 ± 29 | 43 ± 18 | 87 ± 42 | 7 ± 2 | 3 ± 1 | 24 ± 10 | 26 ± 5 |
| NI | 306 (4.9%) | 866 (13.9%) | 269 (4.3%) | 768 (12.3%) | 823 (13.2%) | 1427 (22.9%) | 487 (7.8%) | 362 (5.8%) |
| S | 95.1% | 86.1% | 95.7% | 87.7% | 86.8% | 77.1% | 92.2% | 94.2% |
| 1 ± 0.08 | 1 ± 0.12 | 1 ± 0.08 | 1.1 ± 0.61 | 2.3 ± 1.9 | 2.3 ± 2.4 | 1.2 ± 0.6 | 1.4 ± 1.1 | |
| FP | 280 (5.0%) | 144 (2.9%) | 1301 (18.6%) | 674 (9.0%) | 2374 (16.2%) | 1779 (14.0%) | 1889 (22.3%) | 3088 (27.2%) |
| Artifacts Identified | Movements Detected | |||||
|---|---|---|---|---|---|---|
| MARA | AMARA | AMARAacc | ABAMAR | ABAMAR | AMARAacc | |
| NI | 0 (0%) | 2739 (21.5%) | 2271 (17.8%) | 2410 (18.9%) | 0 (0%) | 686 (8.1%) |
| S | 100% | 78.5% | 82.2% | 81.1% | 100% | 91.9% |
| 1 ± 0.00 | 1 ± 0.07 | 1 ± 0.05 | 1 ± 0.00 | 1 ± 0.00 | 1.2 ± 0.78 | |
| FP | 0 (0%) | 6793 (46.2%) | 5116 (45.1%) | 3195 (37.7%) | 0 (0%) | 1969 (17.4%) |
3. Results
3.1. Validation against the Human Scorers
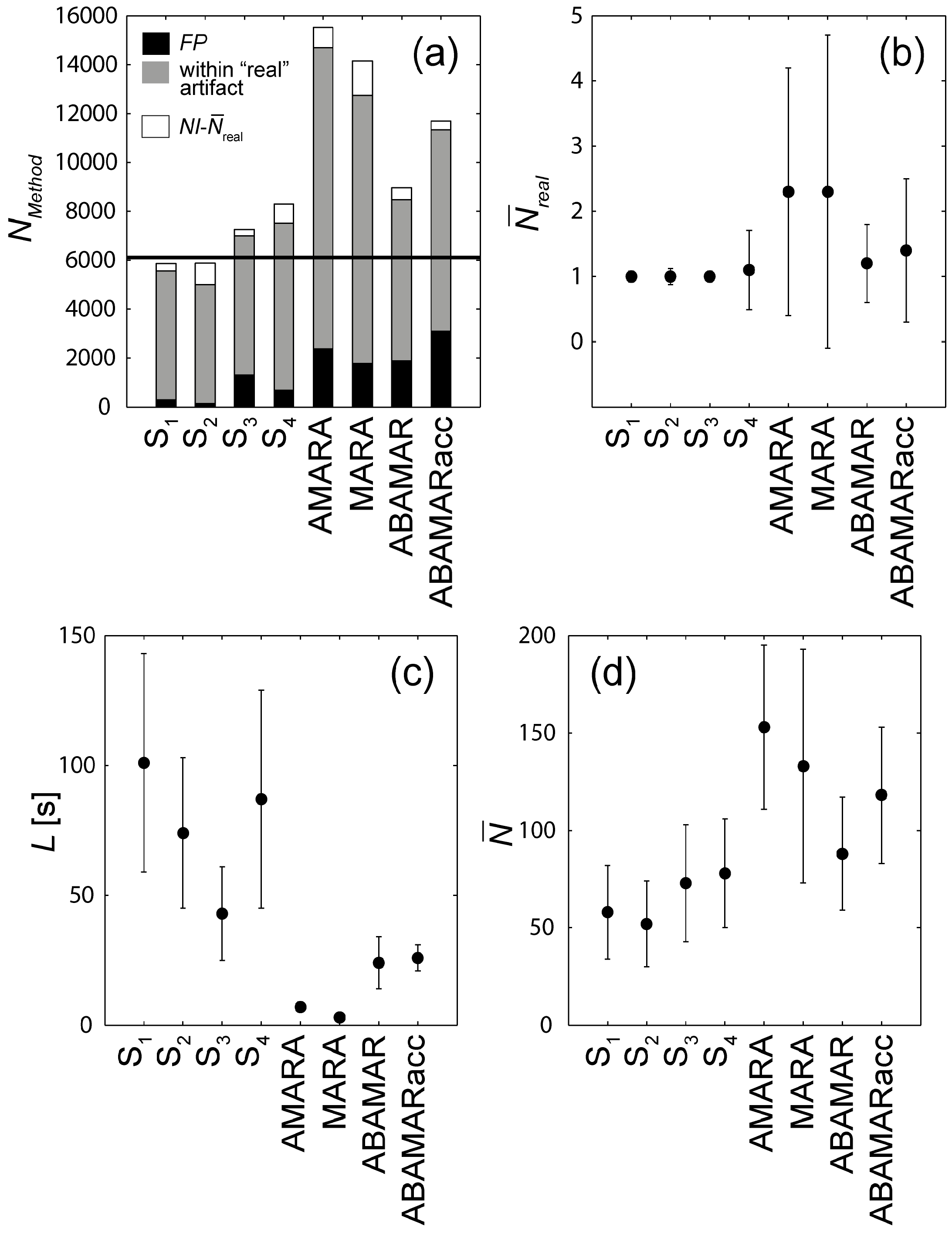

3.2. Comparison of AMARA against MARA
3.3. Validation of the Movement Detection
3.4. Reconstruction
4. Discussion
4.1. Algorithm
4.2. Validation
4.3. Reconstruction
4.4. Limitations of the Proposed AMARA Approach and the Validation
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ferrari, M.; Quaresima, V. A brief review on the history of human functional near-infrared spectroscopy (fNIRS) development and fields of application. NeuroImage 2012, 63, 921–935. [Google Scholar] [CrossRef] [PubMed]
- Scholkmann, F.; Kleiser, S.; Metz, A.J.; Zimmermann, R.; Pavia, J.M.; Wolf, U.; Wolf, M. A review on continuous wave functional near-infrared spectroscopy and imaging instrumentation and methodology. NeuroImage 2014, 85, 6–27. [Google Scholar] [CrossRef] [PubMed]
- Wolf, M.; Ferrari, M.; Quaresima, V. Progress of near-infrared spectroscopy and topography for brain and muscle clinical applications. J. Biomed. Opt. 2007, 12. [Google Scholar] [CrossRef]
- Wolf, M.; Morren, G.; Haensse, D.; Karen, T.; Wolf, U.; Fauchere, J.C.; Bucher, H.U. Near infrared spectroscopy to study the brain: An overview. Opto Electron. Rev. 2008, 16, 413–419. [Google Scholar] [CrossRef]
- Holper, L.; Kobashi, N.; Kiper, D.; Scholkmann, F.; Wolf, M.; Eng, K. Trial-to-trial variability differentiates motor imagery during observation between low versus high responders: A functional near-infrared spectroscopy study. Behav. Brain Res. 2012, 229, 29–40. [Google Scholar] [CrossRef] [PubMed]
- Holper, L.; Scholkmann, F.; Shalom, D.E.; Wolf, M. Extension of mental preparation positively affects motor imagery as compared to motor execution: A functional near-infrared spectroscopy study. Cortex 2012, 48, 593–603. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Holper, L.; Scholkmann, F.; Wolf, M. Between-brain connectivity during imitation measured by fnirs. NeuroImage 2012, 63, 212–222. [Google Scholar] [CrossRef] [PubMed]
- Holper, L.; Scholkmann, F.; Wolf, M. The relationship between sympathetic nervous activity and cerebral hemodynamics and oxygenation: A study using skin conductance measurement and functional near-infrared spectroscopy. Behav. Brain Res. 2014, 270, 95–107. [Google Scholar] [CrossRef] [PubMed]
- Kobashi, N.; Holper, L.; Scholkmann, F.; Kiper, D.; Eng, K. Enhancement of motor imagery-related cortical activation during first-person observation measured by functional near-infrared spectroscopy. Eur. J. Neurosci. 2012, 35, 1513–1521. [Google Scholar] [CrossRef] [PubMed]
- Obrig, H.; Wenzel, R.; Kohl, M.; Horst, S.; Wobst, P.; Steinbrink, J.; Thomas, F.; Villringer, A. Near-infrared spectroscopy: Does it function in functional activation studies of the adult brain? Int. J. Psychophys. 2000, 35, 125–142. [Google Scholar] [CrossRef]
- Scholkmann, F.; Metz, A.J.; Wolf, M. Measuring tissue hemodynamics and oxygenation by continuous-wave functional near-infrared spectroscopy—How robust are the different calculation methods against movement artifacts? Physiol. Meas. 2014, 35, 717–734. [Google Scholar] [CrossRef] [PubMed]
- Biallas, M.; Trajkovic, I.; Hagmann, C.; Scholkmann, F.; Jenny, C.; Holper, L.; Beck, A.; Wolf, M. Multimodal recording of brain activity in term newborns during photic stimulation by near-infrared spectroscopy and electroencephalography. J. Biomed. Opt. 2012, 17. [Google Scholar] [CrossRef]
- Biallas, M.; Trajkovic, I.; Scholkmann, F.; Hagmann, C.; Wolf, M. How to conduct studies with neonates combining near-infrared imaging and electroencephalography. Adv. Exp. Med. Biol. 2012, 737, 111–117. [Google Scholar] [PubMed]
- Greisen, G.; Leung, T.; Wolf, M. Has the time come to use near-infrared spectroscopy as a routine clinical tool in preterm infants undergoing intensive care? Philos. Trans. A Math. Phys. Eng. Sci. 2011, 369, 4440–4451. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wolf, M.; Duc, G.; Keel, M.; Niederer, P.; von Siebenthal, K.; Bucher, H.U. Continuous noninvasive measurement of cerebral arterial and venous oxygen saturation at the bedside in mechanically ventilated neonates. Crit. Care Med. 1997, 25, 1579–1582. [Google Scholar] [CrossRef] [PubMed]
- Gygax, L.; Reefmann, N.; Pilheden, T.; Scholkmann, F.; Keeling, L. Dog behavior but not frontal brain reaction changes in repeated positive interactions with a human: A non-invasive pilot study using functional near-infrared spectroscopy (fNIRS). Behav. Brain Res. 2015, 281, 172–176. [Google Scholar] [CrossRef] [PubMed]
- Muehlemann, T.; Reefmann, N.; Wechsler, B.; Wolf, M.; Gygax, L. In vivo functional near-infrared spectroscopy measures mood-modulated cerebral responses to a positive emotional stimulus in sheep. NeuroImage 2011, 54, 1625–1633. [Google Scholar] [CrossRef] [PubMed]
- Gygax, L.; Reefmann, N.; Wolf, M.; Langbein, J. Prefrontal cortex activity, sympatho-vagal reaction and behaviour distinguish between situations of feed reward and frustration in dwarf goats. Behav. Brain Res. 2013, 239, 104–114. [Google Scholar] [CrossRef] [PubMed]
- Hoshi, Y.; Mizukami, S.; Tamura, M. Dynamic features of hemodynamic and metabolic changes in the human brain during all-night sleep as revealed by near-infrared spectroscopy. Brain Res. 1994, 652, 257–262. [Google Scholar] [CrossRef]
- Kubota, Y.; Takasu, N.N.; Horita, S.; Kondo, M.; Shimizu, M.; Okada, T.; Wakamura, T.; Toichi, M. Dorsolateral prefrontal cortical oxygenation during rem sleep in humans. Brain Res. 2011, 1389, 83–92. [Google Scholar] [CrossRef] [PubMed]
- Metz, A.J.; Pugin, F.; Huber, R.; Achermann, P.; Wolf, M. Changes of cerebral tissue oxygen saturation at sleep transitions in adolescents. Adv. Exp. Med. Biol. 2014, 812, 279–285. [Google Scholar] [PubMed]
- Metz, A.J.; Pugin, F.; Huber, R.; Achermann, P.; Wolf, M. Brain tissue oxygen saturation increases during the night in adolescents. Adv. Exp. Med. Biol. 2013, 789, 113–119. [Google Scholar] [PubMed]
- Nasi, T.; Virtanen, J.; Noponen, T.; Toppila, J.; Salmi, T.; Ilmoniemi, R.J. Spontaneous hemodynamic oscillations during human sleep and sleep stage transitions characterized with near-infrared spectroscopy. PLoS ONE 2011, 6. [Google Scholar] [CrossRef] [PubMed]
- Pizza, F.; Biallas, M.; Wolf, M.; Werth, E.; Bassetti, C.L. Nocturnal cerebral hemodynamics in snorers and in patients with obstructive sleep apnea: A near-infrared spectroscopy study. Sleep 2010, 33, 205–210. [Google Scholar] [PubMed]
- Spielman, A.J.; Zhang, G.; Yang, C.M.; D’Ambrosio, P.; Serizawa, S.; Nagata, M.; von Gizycki, H.; Alfano, R.R. Intracerebral hemodynamics probed by near infrared spectroscopy in the transition between wakefulness and sleep. Brain Res. 2000, 866, 313–325. [Google Scholar] [CrossRef]
- Cui, X.; Bray, S.; Reiss, A.L. Functional near infrared spectroscopy (NIRS) signal improvement based on negative correlation between oxygenated and deoxygenated hemoglobin dynamics. NeuroImage 2010, 49, 3039–3046. [Google Scholar] [CrossRef] [PubMed]
- Izzetoglu, M.; Devaraj, A.; Bunce, S.; Onaral, B. Motion artifact cancellation in NIR spectroscopy using wiener filtering. IEEE Trans. Biomed. Eng. 2005, 52, 934–938. [Google Scholar] [CrossRef] [PubMed]
- Jang, K.E.; Tak, S.; Jung, J.; Jang, J.; Jeong, Y.; Ye, J.C. Wavelet minimum description length detrending for near-infrared spectroscopy. J. Biomed. Opt. 2009, 14. [Google Scholar] [CrossRef] [PubMed]
- Molavi, B.; Dumont, G.A. Wavelet-based motion artifact removal for functional near-infrared spectroscopy. Physiol. Meas. 2012, 33, 259–270. [Google Scholar] [CrossRef] [PubMed]
- Nozawa, T.; Kondo, T. A Comparison of Artifact Reduction Methods for Real-Time Analysis of fNIRS data; Springer Berlin Heidelberg: Heidelberg, Germany, 2009; pp. 413–422. [Google Scholar]
- Wilcox, T.; Bortfeld, H.; Woods, R.; Wruck, E.; Boas, D.A. Using near-infrared spectroscopy to assess neural activation during object processing in infants. J. Biomed. Opt. 2005, 10. [Google Scholar] [CrossRef] [PubMed]
- Yamada, T.; Umeyama, S.; Matsuda, K. Separation of fnirs signals into functional and systemic components based on differences in hemodynamic modalities. PLoS ONE 2012, 7. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Brooks, D.H.; Franceschini, M.A.; Boas, D.A. Eigenvector-based spatial filtering for reduction of physiological interference in diffuse optical imaging. J. Biomed. Opt. 2005, 10. [Google Scholar] [CrossRef] [PubMed]
- Scholkmann, F.; Spichtig, S.; Muehlemann, T.; Wolf, M. How to detect and reduce movement artifacts in near-infrared imaging using moving standard deviation and spline interpolation. Physiol. Meas. 2010, 31, 649–662. [Google Scholar] [CrossRef] [PubMed]
- Bale, G.; Mitra, S.; Meek, J.; Robertson, N.; Tachtsidis, I. A new broadband near-infrared spectroscopy system for in vivo measurements of cerebral cytochrome-c-oxidase changes in neonatal brain injury. Biomed. Opt. Express 2014, 5, 3450–3466. [Google Scholar] [CrossRef] [PubMed]
- Dommer, L.; Jager, N.; Scholkmann, F.; Wolf, M.; Holper, L. Between-brain coherence during joint n-back task performance: A two-person functional near-infrared spectroscopy study. Behav. Brain Res. 2012, 234, 212–222. [Google Scholar] [CrossRef] [PubMed]
- Holper, L.; Muehlemann, T.; Scholkmann, F.; Eng, K.; Kiper, D.; Wolf, M. Testing the potential of a virtual reality neurorehabilitation system during performance of observation, imagery and imitation of motor actions recorded by wireless functional near-infrared spectroscopy (fNIRS). J. Neuroeng. Rehabil. 2010, 7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Spichtig, S.; Scholkmann, F.; Chin, L.; Lehmann, H.; Wolf, M. Assessment of potential short-term effects of intermittent umts electromagnetic fields on blood circulation in an exploratory study, using near-infrared imaging. Adv. Exp. Med. Biol. 2012, 737, 83–88. [Google Scholar] [PubMed]
- Wolf, U.; Scholkmann, F.; Rosenberger, R.; Wolf, M.; Nelle, M. Changes in hemodynamics and tissue oxygenation saturation in the brain and skeletal muscle induced by speech therapy–A near-infrared spectroscopy study. TheScientificWorldJournal 2011, 11, 1206–1215. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cooper, R.J.; Selb, J.; Gagnon, L.; Phillip, D.; Schytz, H.W.; Iversen, H.K.; Ashina, M.; Boas, D.A. A systematic comparison of motion artifact correction techniques for functional near-infrared spectroscopy. Front. Neurosci. 2012, 6. [Google Scholar] [CrossRef] [PubMed]
- Brigadoi, S.; Ceccherini, L.; Cutini, S.; Scarpa, F.; Scatturin, P.; Selb, J.; Gagnon, L.; Boas, D.A.; Cooper, R.J. Motion artifacts in functional near-infrared spectroscopy: A comparison of motion correction techniques applied to real cognitive data. NeuroImage 2013, 85, 181–191. [Google Scholar] [CrossRef] [PubMed]
- Matcher, S.J.; Kirkpatrick, P.; Nahid, K.; Cope, M.; Delpy, D.T. Absolute Quantification Methods in Tissue Near Infrared Spectroscopy. In Proceedings of the Optical Tomography, Photon. Migration, and Spectroscopy of Tissue and Model. Media: Theory, Human Studies, and Instrumentation, San Jose, CA, USA, 1 Febuary 1995; pp. 486–495.
- Suzuki, S.; Takasaki, S.; Ozaki, T.; Kobayashi, Y. Tissue Oxygenation Monitor Using NIR Spatially Resolved Spectroscopy. In Proceedings of the Optical Tomography and Spectroscopy of Tissue Iii, San Jose, CA, USA, 23 January 1999; pp. 582–592.
- Hueber, D.M.; Fantini, S.; Cerussi, A.E.; Barbieri, B. New Optical Probe Designs for Absolute (Self-Calibrating) NIR Tissue Hemoglobin Measurements. In Proceedings of the Optical Tomography and Spectroscopy of Tissue Iii, San Jose, CA, USA, 23 January 1999; pp. 618–631.
- Gagnon, L.; Cooper, R.J.; Yucel, M.A.; Perdue, K.L.; Greve, D.N.; Boas, D.A. Short separation channel location impacts the performance of short channel regression in NIRS. NeuroImage 2012, 59, 2518–2528. [Google Scholar] [CrossRef] [PubMed]
- Gagnon, L.; Perdue, K.; Greve, D.N.; Goldenholz, D.; Kaskhedikar, G.; Boas, D.A. Improved recovery of the hemodynamic response in diffuse optical imaging using short optode separations and state-space modeling. NeuroImage 2011, 56, 1362–1371. [Google Scholar] [CrossRef] [PubMed]
- Gagnon, L.; Yucel, M.A.; Boas, D.A.; Cooper, R.J. Further improvement in reducing superficial contamination in NIRS using double short separation measurements. NeuroImage 2013, 85, 127–135. [Google Scholar] [CrossRef] [PubMed]
- Gregg, N.M.; White, B.R.; Zeff, B.W.; Berger, A.J.; Culver, J.P. Brain specificity of diffuse optical imaging: Improvements from superficial signal regression and tomography. Front. Neuroenerg 2010, 2. [Google Scholar] [CrossRef] [PubMed]
- Heiskala, J.; Kolehmainen, V.; Tarvainen, T.; Kaipio, J.P.; Arridge, S.R. Approximation error method can reduce artifacts due to scalp blood flow in optical brain activation imaging. J. Biomed. Opt. 2012, 17, 96012–96011. [Google Scholar] [CrossRef] [PubMed]
- Robertson, F.C.; Douglas, T.S.; Meintjes, E.M. Motion artifact removal for functional near infrared spectroscopy: A comparison of methods. IEEE Trans. Biomed. Eng. 2010, 57, 1377–1387. [Google Scholar] [CrossRef] [PubMed]
- Saager, R.; Berger, A. Measurement of layer-like hemodynamic trends in scalp and cortex: Implications for physiological baseline suppression in functional near-infrared spectroscopy. J. Biomed. Opt. 2008, 13. [Google Scholar] [CrossRef] [PubMed]
- Saager, R.B.; Berger, A.J. Direct characterization and removal of interfering absorption trends in two-layer turbid media. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2005, 22, 1874–1882. [Google Scholar] [CrossRef] [PubMed]
- Saager, R.B.; Telleri, N.L.; Berger, A.J. Two-detector corrected near infrared spectroscopy (c-NIRS) detects hemodynamic activation responses more robustly than single-detector NIRS. NeuroImage 2011, 55, 1679–1685. [Google Scholar] [CrossRef] [PubMed]
- Scarpa, F.; Brigadoi, S.; Cutini, S.; Scatturin, P.; Zorzi, M.; Dell’Acqua, R.; Sparacino, G. A methodology to improve estimation of stimulus-evoked hemodynamic response from fNIRS measurements. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2011, 2011, 785–788. [Google Scholar] [PubMed]
- Tanaka, H.; Katura, T.; Sato, H. Task-related component analysis for functional neuroimaging and application to near-infrared spectroscopy data. NeuroImage 2013, 64, 308–327. [Google Scholar] [CrossRef] [PubMed]
- Tian, F.H.; Niu, H.J.; Khan, B.; Alexandrakis, G.; Behbehani, K.; Liu, H.L. Enhanced functional brain imaging by using adaptive filtering and a depth compensation algorithm in diffuse optical tomography. IEEE Trans. Med. Imaging 2011, 30, 1239–1251. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Brown, E.N.; Strangman, G.E. Adaptive filtering for global interference cancellation and real-time recovery of evoked brain activity: A monte carlo simulation study. J. Biomed. Opt. 2007, 12. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Brown, E.N.; Strangman, G.E. Adaptive filtering to reduce global interference in evoked brain activity detection: A human subject case study. J. Biomed. Opt. 2007, 12. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Niu, H.J.; Song, Y.; Fan, Y. Activation Detection in fNIRS by Wavelet Coherence. In Proceedings of the Medical Imaging 2012: Biomedical Applications in Molecular, Structural, and Functional Imaging, San Diego, CA, USA, 4 February 2012. [CrossRef]
- Naseer, N.; Hong, K.S. Fnirs-based brain-computer interfaces: A review. Front. Hum. Neurosci. 2015, 9. [Google Scholar] [CrossRef] [PubMed]
- Kamran, M.A.; Hong, K.S. Reduction of physiological effects in fnirs waveforms for efficient brain-state decoding. Neurosci. Lett. 2014, 580, 130–136. [Google Scholar] [CrossRef] [PubMed]
- Santosa, H.; Hong, M.J.; Kim, S.P.; Hong, K.S. Noise reduction in functional near-infrared spectroscopy signals by independent component analysis. Rev. Sci. Instrum. 2013, 84. [Google Scholar] [CrossRef] [PubMed]
- Virtanen, J.; Noponen, T.; Kotilahti, K.; Ilmoniemi, R.J. Accelerometer-based method for correcting signal baseline changes caused by motion artifacts in medical near-infrared spectroscopy. J. Biomed. Opt. 2011, 16. [Google Scholar] [CrossRef] [PubMed]
- Zack, G.W.; Rogers, W.E.; Latt, S.A. Automatic measurement of sister chromatid exchange frequency. J. Histochem. Cytochem. 1977, 25, 741–753. [Google Scholar] [CrossRef] [PubMed]
- Savitzky, A.; Golay, M.J.E. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Muehlemann, T.; Haensse, D.; Wolf, M. Wireless miniaturized in vivo near infrared imaging. Opt. Express 2008, 16, 10323–10330. [Google Scholar] [CrossRef] [PubMed]
- Kurihara, K.; Kikukawa, A.; Kobayashi, A. Cerebral oxygenation monitor during head-up and-down tilt using near-infrared spatially resolved spectroscopy. Clin. Phys. Funct. Imaging 2003, 23, 177–181. [Google Scholar] [CrossRef]
- Scholkmann, F.; Wolf, M.; Wolf, U. The effect of inner speech on arterial CO2 and cerebral hemodynamics and oxygenation: A functional nirs study. Adv. Exp. Med. Biol. 2013, 789, 81–87. [Google Scholar] [PubMed]
- Scholkmann, F.; Gerber, U.; Wolf, M.; Wolf, U. End-tidal CO2: An important parameter for a correct interpretation in functional brain studies using speech tasks. NeuroImage 2013, 66, 71–79. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Metz, A.J.; Wolf, M.; Achermann, P.; Scholkmann, F. A New Approach for Automatic Removal of Movement Artifacts in Near-Infrared Spectroscopy Time Series by Means of Acceleration Data. Algorithms 2015, 8, 1052-1075. https://0-doi-org.brum.beds.ac.uk/10.3390/a8041052
Metz AJ, Wolf M, Achermann P, Scholkmann F. A New Approach for Automatic Removal of Movement Artifacts in Near-Infrared Spectroscopy Time Series by Means of Acceleration Data. Algorithms. 2015; 8(4):1052-1075. https://0-doi-org.brum.beds.ac.uk/10.3390/a8041052
Chicago/Turabian StyleMetz, Andreas Jaakko, Martin Wolf, Peter Achermann, and Felix Scholkmann. 2015. "A New Approach for Automatic Removal of Movement Artifacts in Near-Infrared Spectroscopy Time Series by Means of Acceleration Data" Algorithms 8, no. 4: 1052-1075. https://0-doi-org.brum.beds.ac.uk/10.3390/a8041052






