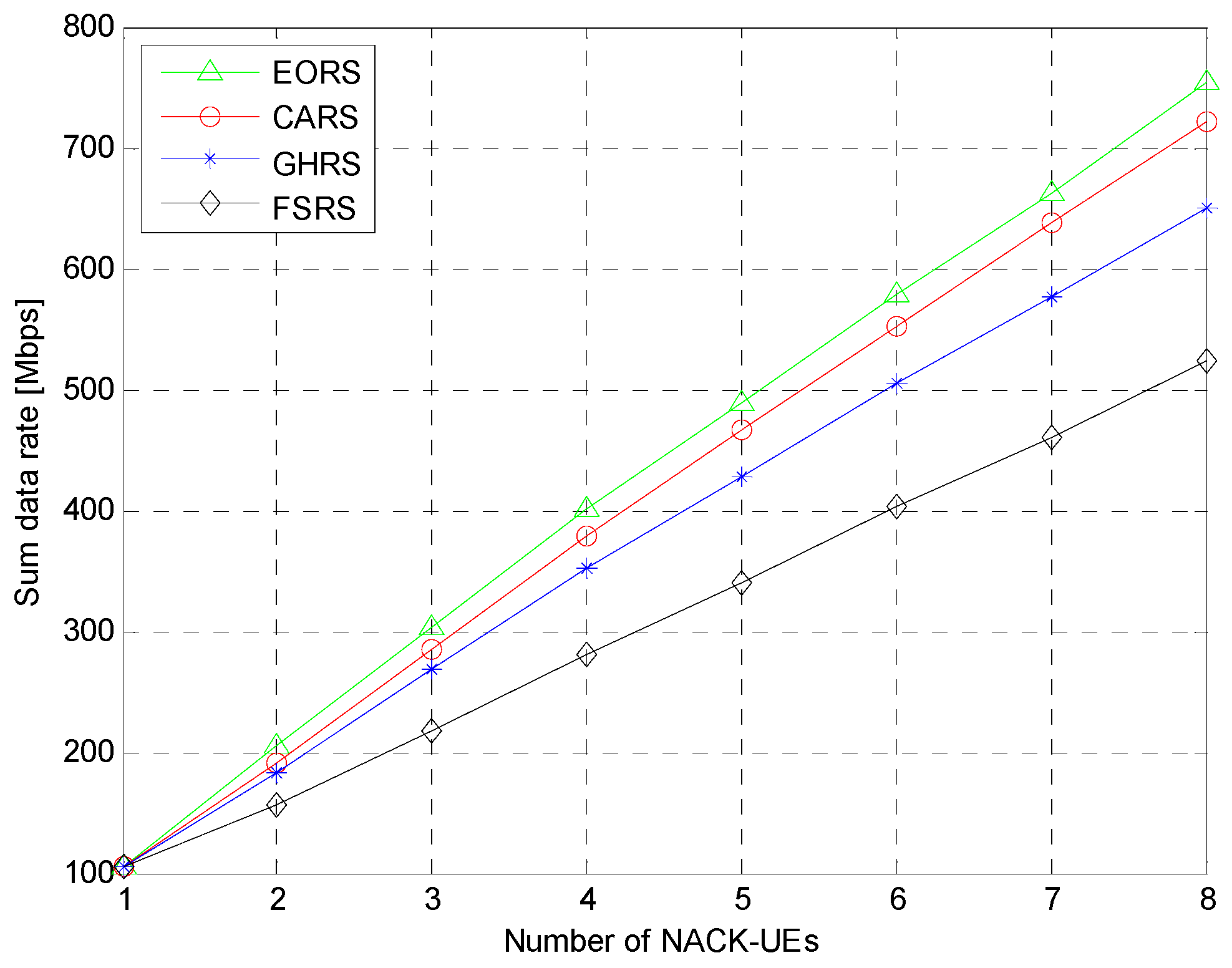
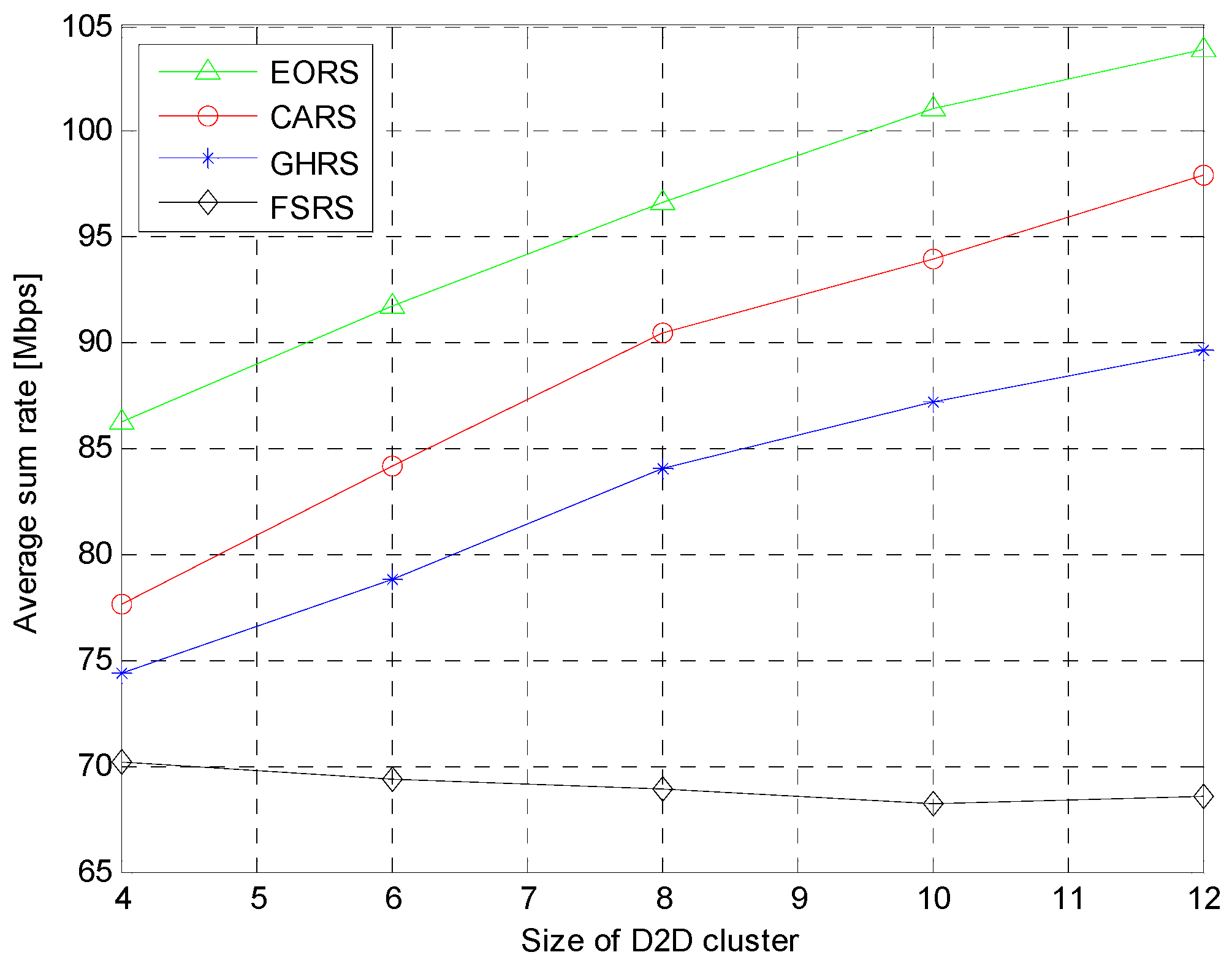
1. Introduction
The standard solution for supporting multicast services in Long Term Evolution-Advanced (LTE-A) networks suffers from severe inefficiencies [
1], as the conventional cellular multicast performance is strictly bounded by the user with the poorest channel conditions. For this reason, researchers are active in studying solutions to enhance the multicast services performance in cellular systems [
1]. Among many alternatives, another new paradigm within LTE-A systems, namely Device-to-Device (D2D) communications [
2], has become a flourishing research field. D2D communication is about enabling direct flow of data among User Equipments (UEs) in close proximity, it holds merit of data offloading for the eNodeB (eNB), improving spectrum efficiency, and increasing system capacity [
2,
3,
4],
etc. These observations led us to the idea of bringing D2D communications into the cellular multicast services framework, and investigating the potentialities of adopting D2D communications to enhance the performance of conventional multicast services.
In LTE-A networks, UEs requesting the same data from eNB can be grouped into a cluster and eNB multicasts data to all UEs within the cluster. The major issue in cellular multicast transmissions is the different channel conditions for the multicast recipients. Alternatively in D2D-assisted networks, UEs with good channel conditions are enabled to act as relays to communicate the received multicast data from the eNB to the remaining UEs via D2D links, such that the eNB can multicast at a high data rate and the transmission efficiency is improved. Based on this idea, in [
5] the authors proposed a cooperative multicast transmission scheme,
i.e., in which all successful multicast recipients participate in D2D relay transmissions by broadcasting their received data on the same resource. Because each D2D relay should serve all failed multicast recipients at a common rate selected according to the worst D2D link, it is unfavorable to improve the network throughput. In [
6] the authors assumed a single predefined multicast recipient called cluster head which is responsible for D2D relay transmissions. Unfortunately the efficiency of this scheme is not guaranteed in case the predesignated recipient fails to receive multicast data and the eNB must participate in retransmissions. In [
7] the authors proposed an adaptive D2D retransmission scheme exploiting the multi-channel diversity to improve spectrum, which adaptively selects the optimal number of D2D retransmitters and conducts the optimal sub-cluster partition. Furthermore, in [
8] authors introduced relay based transmission into the multicast process so as to overcome transmission rate restriction caused by link heterogeneity, and a greedy heuristic algorithm was applied to select relay nodes. According to the these works, to improve the transmission quality of intra-cluster multicast service, a high efficient relay selection should be considered in the D2D cluster.
In this paper we consider an auction-based approach using game theory. A combinatorial auction (CA) model for resource management was introduced in [
9]. Combinatorial auctions are multi-item or multi-bidder auctions in which bidders can form combinations called packages, rather than just bid individually. Furthermore, in the evolution auction mechanisms named iterative combinatorial auctions [
10], the step of bid evaluation is executed multiple times, and the auctioneer computes provisional allocations in each auction round. Iterative CAs have already found applications in allocating radio spectrum for wireless communications [
11]. The CAs motivate bidders to fully express their preferences, which is an advantage in improving system efficiency and auction revenues. Up to that point, we study an effective D2D relay selection for multicast services to further improve system efficiency based on the iterative CA. The whole system consists of the eNB, multiple successful multicast recipients, and multiple failed multicast recipients. Considering that an efficient exploitation of multi-channel diversity may bring large beneficial to system throughout, we formulate the problem as a CA game. By this way, the failed multicast recipients and the successful multicast recipients are regarded as bidders and goods, respectively, while the successful multicast recipients are goods waiting to be selected as relays. Each bidder has a valuation for the relays, and multiple bidders can form a package that share the same relay. During the auction, the bidders submit bids and the auctioneer,
i.e., the eNB decides the allocation of the relays. Furthermore, we propose an auction algorithm which runs iteratively until reaching an equilibrium state. We also discuss the properties of our algorithm and the simulation results show a good performance on the sum data rate and system efficiency.
The rest of the paper is organized as follows. In
Section 2, a system model of intra-cluster D2D communication is introduced. Then we formulate the primary problem as a CA game in
Section 3. Next, in
Section 4, the CA algorithm for D2D relay selection is proposed, and the main properties of the proposed algorithm are discussed. In
Section 5, we present the simulation results. Finally, we conclude this paper in
Section 6.
2. System Model
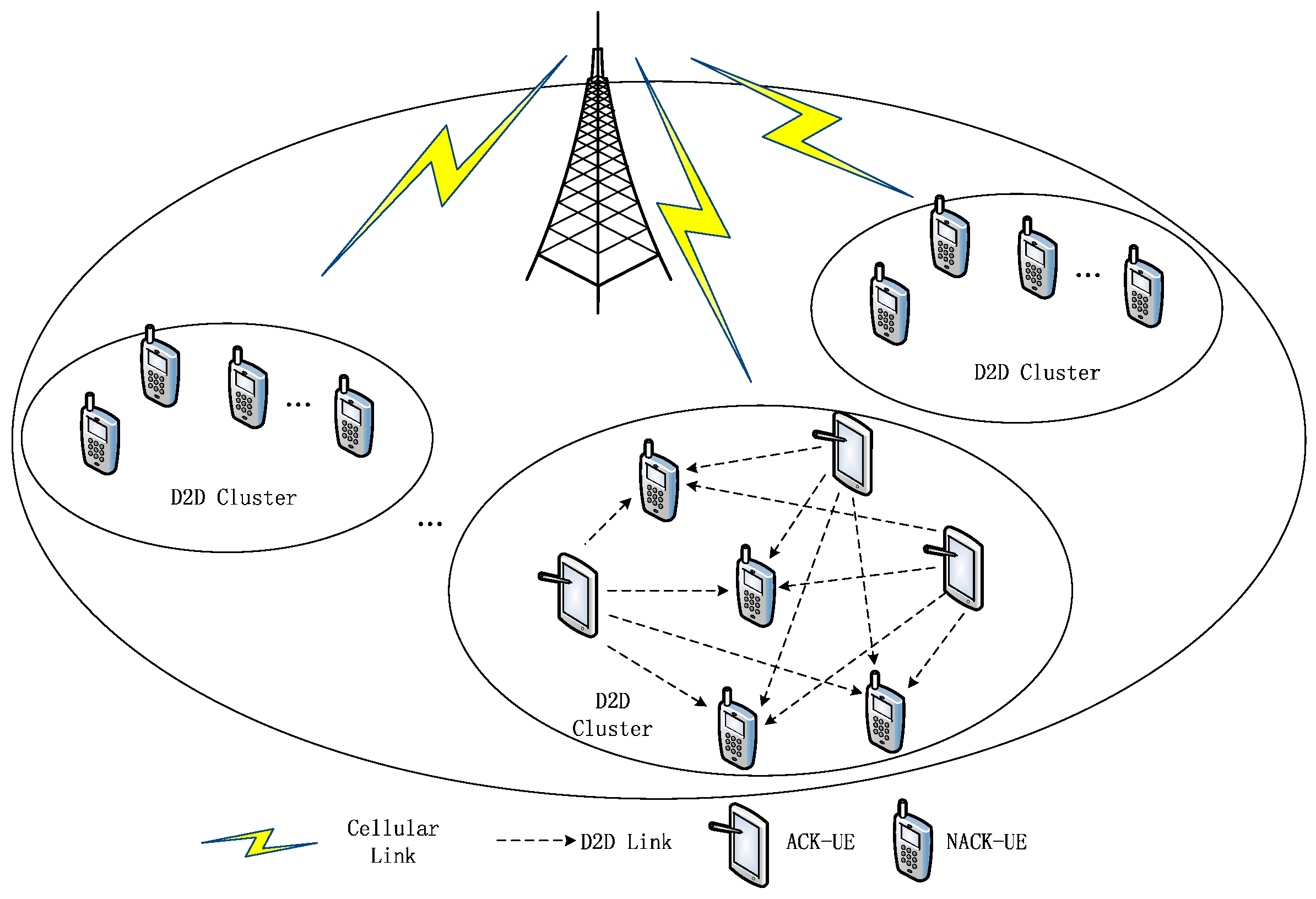
We consider a single-cell multicast system where an eNB serves numerous UEs and the UEs in close proximity can group into a cluster to request the same data from eNB. The UEs within a cluster can not only communicate with eNB, but also directly communicate with each other via D2D links. Let us focus on one D2D cluster, as illustrated in
Figure 1. Due to independent properties of cellular downlink channels, when the eNB multicasts data to all UEs within a D2D cluster at a certain rate, only a portion of the UEs can correctly receive and decode the data. The UEs that can and cannot successfully receive data are referred to as “ACK-UEs” and “NACK-UEs”, respectively. In order to share the data from eNB in the whole cluster, ACK-UEs can be employed as relays to forward the received data to NACK-UEs via D2D links. In general, the underlined intra-cluster relay transmissions can be accomplished via D2D multicast. Meanwhile, to avoid the interference between D2D communication and cellular communication, orthogonal resources should be allocated to them.
Figure 1.
D2D clusters with ACK-UEs and NACK-UEs in the cellular network.
Figure 1.
D2D clusters with ACK-UEs and NACK-UEs in the cellular network.
In the paper, we only consider both large-scale path-loss attenuation and smallscale fading characterized by Rayleigh fading, and thus the channel response follows the independent complex Gaussian distribution. In addition, the free space propagation path-loss model,
, is used where
and
represent signal power measured at
and
meters away from the transmitter, respectively.
is a path-loss exponent. We simplify the received power at
equals the transmit power. Hence, the received power of each D2D link can be expressed as.
where
and
are the received power and the distance of the
i–
j link.
represents the transmit power of UE
, and
is the complex Gaussian channel coefficient that obeys the distribution
. Given the power spectral density of the additive Gaussian noise
and system bandwidth
, according to Shannon formula, the channel rate of UE
j can be obtained by.
We define
is the set of NACK-UEs and
is the set of ACK-UEs. The numbers of NACK-UEs and ACK-UEs in the cluster are denoted as
and
, respectively. Besides, inspired by [
7], we assume there are
ACK-UEs acting as relays. For a given relay, the achievable D2D multicast rate depends on the worst link among all links connecting it with all NACK-UEs. By optimizing selecting of a D2D relay, the system sum data rate can be defined as
where
stands for the index of an ACK-UE acting as the
i-th D2D relay. The optimal D2D relay selection is performed under constraints
, and
, to guarantee that each NACK-UE in the cluster should be served by one relay. Although Equation (3) gives a generic solution, this optimization problem is very complicated in general. Therefore, it is necessary to design a relay selection mechanism that is not only computationally tractable, but also able to sustain high system efficiency.
3. Problem Formulation
In the proposed D2D cluster, system sum data rate is considered as the central optimization problem. As ACK-UEs are selected as relays to serve NACK-UEs, the contributions to system data rate are various due to heterogeneity of the D2D links between relays and NACK-UEs. Therefore, in order to optimize the system performance, we focus on the how NACK-UEs are effectively allocated to ACK-UEs for the sake of relay services.
In this section, based on Equation (3), we can model the D2D relay selection process as a CA game. In this auction, NACK-UEs are considered as the bidders who bid to get a certain item, i.e., ACK-UE, while the eNB is the auctioneer. Since multiple NACK-UEs can be served by one D2D relay, the packages of NACK-UEs can form combinatorial bidders. We denote
as the set of bidders participating in the auction
and denote
as a specific bidder. Similarly, we denote
as the set of items to be auctioned
and denote
as a specific item. We also denote the set of all possible NACK-UEs packages by , in which an element package is expressed as in correspondence with the m-th ACK-UE. The possible packages are subsets of NACK-UEs. By using
, we can transform the optimization problem in Equation (3) into a package assignment process. We consider a set of binary variables
to define the allocation,
.
indicates that NACK-UE
bidding for ACK-UE
is assigned into package
. In the auction, the goal of the eNB is to maximize the total revenue by selling ACK-UEs. Meanwhile, each NACK-UE targets at purchasing the item to maximize its own package utility.
In order to describe the allocation outcome intuitively, we give the definition below.
Definition 1. The result of the auction is an allocation denoted by, which allocates a corresponding bidder package to every item. And the allocated packages are not intersect: .
To motivate the bidders to reveal their true preferences, we express NACK-UE
’s valuation for ACK-UE
as channel data rate
. Then, the private valuation of package
can be expressed as:
Although the NACK-UEs obtains D2D data rate by getting a D2D relay service of ACK-UE, there exists some cost such as control signals transmission and information feedback during the relay selection process. We define the cost as a pay price. For ACK-UE
, the pay price by the NACK-UE
in package
is written as
. Based on Equation (4), the combinatorial utility of the bidder can be expressed as , in which
is the price set, i.e., . Then We define the allocation vector as
, then the auctioneer (the eNB) revenue can be expressed as
, which is usually considered to be the auctioneer’s gain.
If given an allocation
, it can easily be shown that the overall gain, which includes the total gain of the auctioneer and all bidders does not depend on the pay prices, but is equal to the sum of the allocated packages’ valuations [
10],
i.e.,
As our original intention, we employ the CA to obtain an efficient allocation for D2D relays.
Definition 2. An efficient allocation is an allocation that maximizes the overall gain. The efficient allocation is denoted by
.
Given the private valuations for all possible bidder packages in Equation (4), the efficient allocation can be obtained by solving the Combinatorial Allocation Problem (CAP) in CA games. Thus, the combinatorial NACK-UEs auction can be formulated as
We note that the first constraint ensures that at most one bidders package can be allocated to each ACK-UE. The second constraint guarantees that the bidder-overlapping packages can never be assigned. The CAP is also referred to as the winner determine problem, which has been proved that no polynomial time algorithm can be constructed for achieving the reasonable worst case guarantee [
12],
i.e., the problem is NP hard. In the next section, instead of directly solving the NP-hard CAP in Equation (6), we introduce an approximate solution with a computationally tractable auction process to obtain the efficient NACK-UEs allocation.
4. Combinatorial Auction Algorithm
In this section, we first propose an iterative combinatorial auction mechanism, in which the bid allocation choices are determined by an iterative, multi-round auction process. Then, the auction-based algorithm is described in detail and important properties of the proposed algorithm are analyzed.
| Algorithm 1 Algorithm for D2D relay selection |
- 1:
Initialize packages to be empty set. - 2:
Set up the history function of bidder for package is , , . - 3:
for each do - 4:
for each do - 5:
Calculate valuation according to (2); - 6:
Bidder submits bids for item ; - 7:
end for - 8:
end for - 9:
for each do - 10:
Auctioneer finds the maximum valuation and sells the ACK-UE to bidder ; - 11:
Allocate to package : ; - 12:
end for - 13:
Calculate combinatorial valuation of each package according to (4); - 14:
loop until : - 15:
Initialize , ; - 16:
for each do - 17:
if then - 18:
break; - 19:
else - 20:
Find the package that is in; - 21:
Try to remove from package , and calculate the consequent valuation ; - 22:
if then - 23:
, - 24:
end if - 25:
end if - 26:
end for - 27:
for each do - 28:
Bidder submits bid , the auctioneer calculate valuation ; - 29:
if then - 30:
, ; - 31:
end if - 32:
end for - 33:
if then - 34:
Update the provisional allocation: , ; - 35:
; - 36:
else - 37:
break; - 38:
end if - 39:
end loop
|
4.1. Algorithm for D2D Relay Selection
At the beginning of the auction, the eNB collects the location information of UEs and gets the channel state information (CSI) for all the links between UEs and the eNB. The bidders, i.e., the NACK-UEs evaluate all their D2D links connecting to the ACK-UEs to obtain their valuations. In the first round, all bidders submit bids for each ACK-UE. Let
denote the submitted bid by bidder
and
the bid equal to its valuation for item
. The auctioneer finds the highest bid
, and sells the ACK-UE
to bidder
. Then
is added to package
. The auction process moves on until all the bidders obtain an item. Then, the auction enters the second round.
In the auction, the ACK-UEs is allowed to be sold more than once, but the bidder can only be allocated one item. That means, at the end of the first round, we can get a provisional allocation
, in which each element corresponds to a bidder package (possibly empty). To improve the outcome of the first round, the auctioneer adjusts the auction results in the second round. Given each combinatorial valuation
calculated according to Equation (2), the available adjustment strategies of the auctioneer and bidders are classified as follows
- (1)
Try to remove each bidder
from its package
and calculate the consequent combinatorial valuation
.
- (2)
Find the maximum value from the set
and select the corresponding
which is marked as
.
- (3)
Bidder
submits bid
, and then the auctioneer tries to add the bidder
into package
and calculates the consequent combinatorial valuation
.
- (4)
Find the maximum value from the set
and select the corresponding
which is marked as
.
- (5)
The auctioneer checks this adjustment for validity. If
, then updates the provisional allocation, i.e.,
,
, otherwise the above adjustment strategies are invalid.
- (6)
Combinations of items 1–5.
We define history function
, which represents, for every provisional allocation
in the second round, the number of times that bidder
is adjusted into the package
. Further, we also set a strategy constraint which does not allow each bidder is adjusted into the same package
for more than once, i.e.,
. The proposed algorithm with a strategy constraint is summarized in Algorithm 1.
4.2. Convergence
Proposition 1: The proposed algorithm based on the iterative CA with a strategy constraint has the convergence property that the number of the iterations is finite.
Proof: According to the algorithm, in the first round, NACK-UEs are allocated sequentially. Let us focus on the combinatorial auction in the second round. Suppose that the algorithm does not converge after a limited number of iterations, i.e., after T (positive integer) iterations. In this regard, denoting by
the provisional allocation reached at the end of any iteration t, the outcome of proposed algorithm consists of an allocation sequence such as the following:
According to the pigeonhole principle, there exists an allocation
that occurs more than
times, where
denote the set of all possible allocations. Again, according to the pigeonhole principle, there exists a NACK-UE
that is allocated to package
for more than
times, where
. We suppose that
. Then after
T iterations, a history function
corresponding with the NACK-UE
satisfies
which contradicts our constraint. Thus in the second round, the proposed algorithm with a constraint must converge after
T iterations, where
T is a finite number.
4.3. Complexity
As mentioned before, a traditional CAP in fact is an NP hard problem, the number of items to be allocated is M, and the number of bidders is N. For an exhaustive optimal algorithm, an item can be allocated with N possible results. Thus, all the M items are allocated with
possible results. The complexity of the algorithm can be denoted by
. In the first round of the proposed algorithm, every channel is evaluated for all D2D pairs, resulting in a computation of
. In the second round, since each NACK-UE can only be adjusted to the same package no more than once, the complexity is
. Thus, the complexity of the proposed algorithm is
. It is obvious that for sufficient large values of M and N, a finite number of T, a lower complexity is obtained by using the proposed iterative CA scheme. That is,
.
4.4. Feedback and Signaling Overhead
In the D2D cluster, each cluster member should have the knowledge of
and
. This can be achieved by employing one of the existing NACK-based feedback schemes [
13]. At the same time, as periodical D2D channel probing and estimation are indispensable for any cluster setup and maintenance procedure, we assume that each cluster member is always made aware of the channel state information (CSI) of D2D links connecting itself and the others. The additional information needed in our scheme is CSI between ACK-UEs and NACK-UEs, which is much less than the full D2D CSI maintenance. Then, the following iteration process is all conducted at the eNB, and no signal overhead needs to be exchanged among the network nodes until the control signal forwarding. In addition, the future work on D2D relay selection could consider some mechanism that limits the number of NACK-UEs connecting to the same ACK-UE by distance constraint, sociality constraint, etc, which would obviously help to reduce the overhead.