A Data Analytic Algorithm for Managing, Querying, and Processing Uncertain Big Data in Cloud Environments
Abstract
:1. Introduction
- Veracity, which focuses on the quality of data (e.g., uncertainty, messiness, or trustworthiness of data);
- Velocity, which focuses on the speed at which data are collected or generated;
- Value, which focuses on the usefulness of data;
- Variety, which focuses on differences in types, contents or formats of data; and
- Volume, which focuses on the quantity of data.
- The mapper applies a mapping function to each value in the list of values and returns the resulting list;
- The reducer applies a reducing function to combine all the values in the list of values and returns the combined result.
- handling machine failures,
- managing inter-machine communication,
- partitioning the input data, or
- scheduling and executing the program across multiple machines.
- Mining of frequent patterns [23], and
- Formation of association rules (by using the mined frequent patterns as antecedents and consequences of the rules).
2. Background and Related Works
2.1. Big Data Mining with the MapReduce Model
2.2. Constrained Mining
- Frequency constraints include the following:
- sup(X) ≥ minsup expresses the user interest in finding frequent patterns from precise data, i.e., every pattern X with actual support (or frequency) meeting or exceeding the user-specified minimum support threshold minsup; and expSup(X) ≥ minsup expresses the user interest in finding frequent patterns from uncertain data, i.e., every pattern X with expected support meeting or exceeding the user-specified minimum support threshold minsup.
- Non-frequency AM constraints, with examples include the following:
- min(X.RewardPoints) ≥ 2000 expresses the user interest in finding every pattern X such that the minimum reward points earned by travellers among all airports visited are at least 2000;
- max(X.Rainfall) ≤ 10 mm says that the maximum rainfall among all meteorological records in X is at most 10 mm (i.e., “relatively dry”);
- X.Location = Europe expresses the user interest in finding every pattern X such that all places in X are located in Europe;
- X.Weight ≤ 23 kg says that the weight of each object in X is at most 23 kg (e.g., no heavy checked baggage for a trip); and
- sum(X.Expenses) < 300 CHF says that the total expenses on all items in X is less than 300 CHF.
2.3. Uncertain Data Mining
3. MrCloud: Our Data Analytic Algorithm
3.1. Managing Uncertain Big Data
| TID | Content |
|---|---|
| {AMS: 0.9, BCN: 1.0, CPH: 0.5, DEL: 0.9, EDI: 1.0, FRA: 0.2} | |
| {AMS: 0.8, BCN: 0.8, CPH: 1.0, EDI: 0.2, FRA: 0.2, IST: 0.6} | |
| {AMS: 0.4, FRA: 0.2, GUM: 1.0, HEL: 0.5} |
| IATA Code | Airport | Reward Points |
|---|---|---|
| AMS | Amsterdam | 2400 |
| BCN | Barcelona | 3000 |
| CPH | Copenhagen | 2600 |
| DEL | Delhi | 3200 |
| EDI | Edinburgh | 2000 |
| FRA | Frankfurt | 2200 |
| GUM | Guam | 1800 |
| HEL | Helsinki | 2800 |
| IST | Istanbul | 1600 |
3.2. Querying Uncertain Big Data
- difference(X.Temperature) = max(X.Temperature) − min(X.Temperature) ≤ 10 °C says that the difference between the maximum and minimum temperatures in X is at most 10 °C (which involves the difference between two aggregate functions maximum and minimum).
- [min(X.Temperature) ≥ 20 °C] ∧ [max(X.Temperature) ≤ 30 °C] expresses the user interest in finding every pattern X with temperature between 20 °C to 30 °C inclusive (which involves a logical conjunction “AND” of two AM constraints);
- [min(X.RewardPoints) ≥ 2000] ∧ [X.Location = Europe] expresses the user interest in finding every pattern X such that the minimum reward points earned by travellers among all European airports visited are at least 2000 (which again involves a logical conjunction “AND” of two AM constraints); and
- [min(X.Temperature) ≥ 20 °C] ∨ [max(X.Rainfall) ≤ 10 mm] expresses the user interest in finding all meteorological records matching “warm” or “relatively dry” patterns (which involves a logical conjunction “OR” of two AM constraints).
| Classification | Constraints |
|---|---|
| AM | X.attribute θ constant, where |
| max(X.attribute) θ constant, where | |
| min(X.attribute) θ constant, where | |
| sum(X.attribute) θ constant, where | |
| , where and are AM constraints | |
| , where and are AM constraints | |
| non-AM | max(X.attribute) θ constant, where |
| min(X.attribute) θ constant, where | |
| sum(X.attribute) θ constant, where | |
| avg(X.attribute) θ constant, where |
3.3. Processing Uncertain Big Data
- If a pattern X is frequent (i.e., expSup(X) ≥ minsup), then all subsets of X are guaranteed to satisfy the AM constraints because expSup() ≥ expSup(X) ≥ minsup for every subset .
- If a pattern Y is infrequent (i.e., expSup(Y) < minsup), then all supersets of Y are guaranteed to be infrequent because expSup() < expSup(Y) < minsup for every superset . Thus, every superset of Y can be pruned.
- If a pattern X satisfies AM constraints, then all subsets of X are guaranteed to satisfy the AM constraints.
- If a pattern Y does not satisfy AM constraints, then all supersets of Y are guaranteed not to satisfy the AM constraints and thus can be pruned.
for each tj ∈ partition of the uncertain big data do
for each item x ∈ tj and {x} satisfies CAM do
emit 〈x, P(x, tj)〉.
for each x ∈ 〈valid x,list of P(x,tj)〉 do
set expSup({x}) = 0;
for each P(x,tj) ∈ list of P(x,tj) do
expSup({x}) = expSup({x}) + P(x,tj);
if expSup({x}) ≥ minsup then
emit 〈{x},expSup({x})〉.
for each tj ∈ partition of the uncertain big data do
for each {x} ∈ 〈{x}, expSup({x})〉 do
if prefix of tj ending with x contains items besides x then
emit 〈{x}, prefix of tj ending with x〉.
for each x ∈ {x}-projected database do build a tree for {x}-projected database to find X; if X satisfies CAM and expSup(X) ≥ minsup then emit 〈X, expSup(X)〉.
4. Evaluation Results
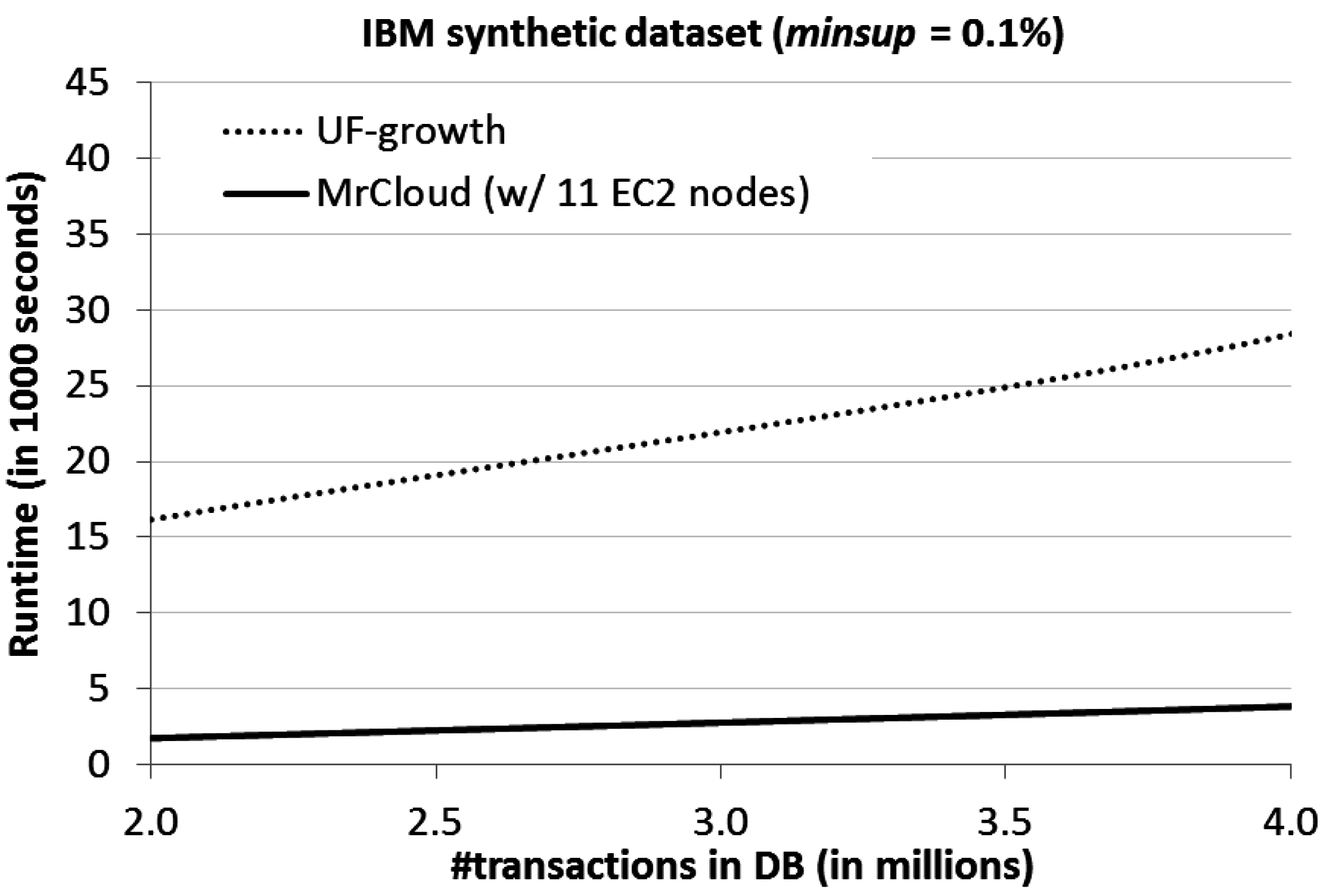
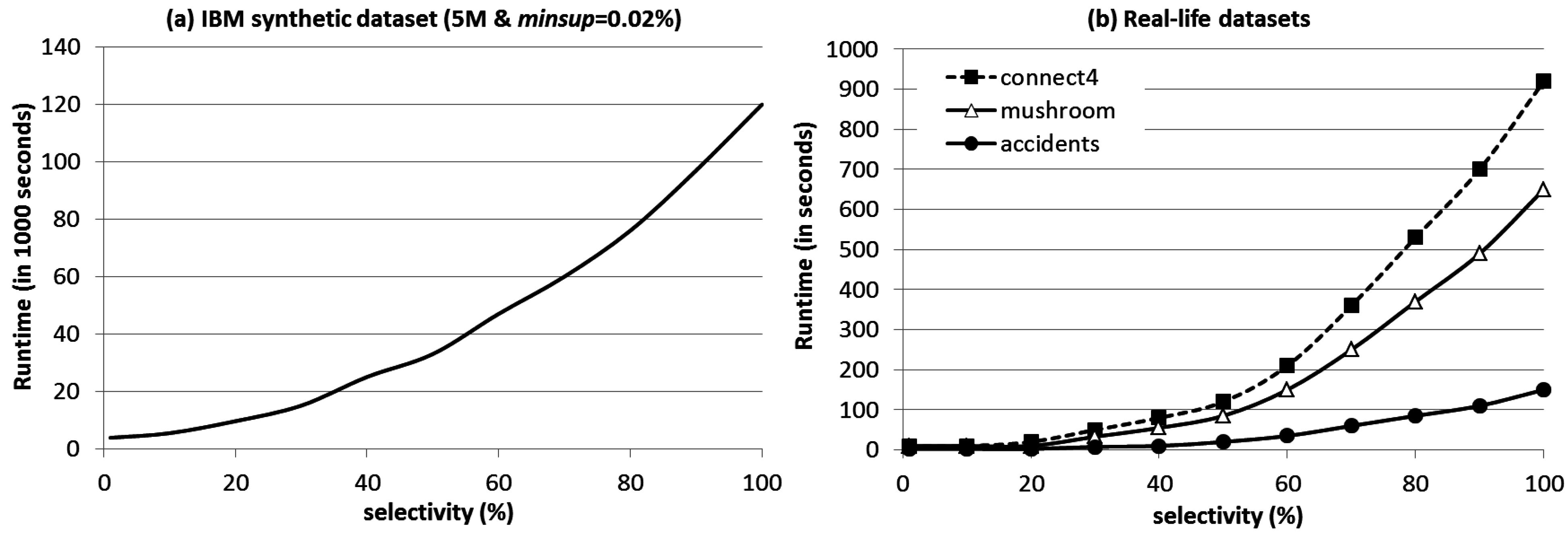

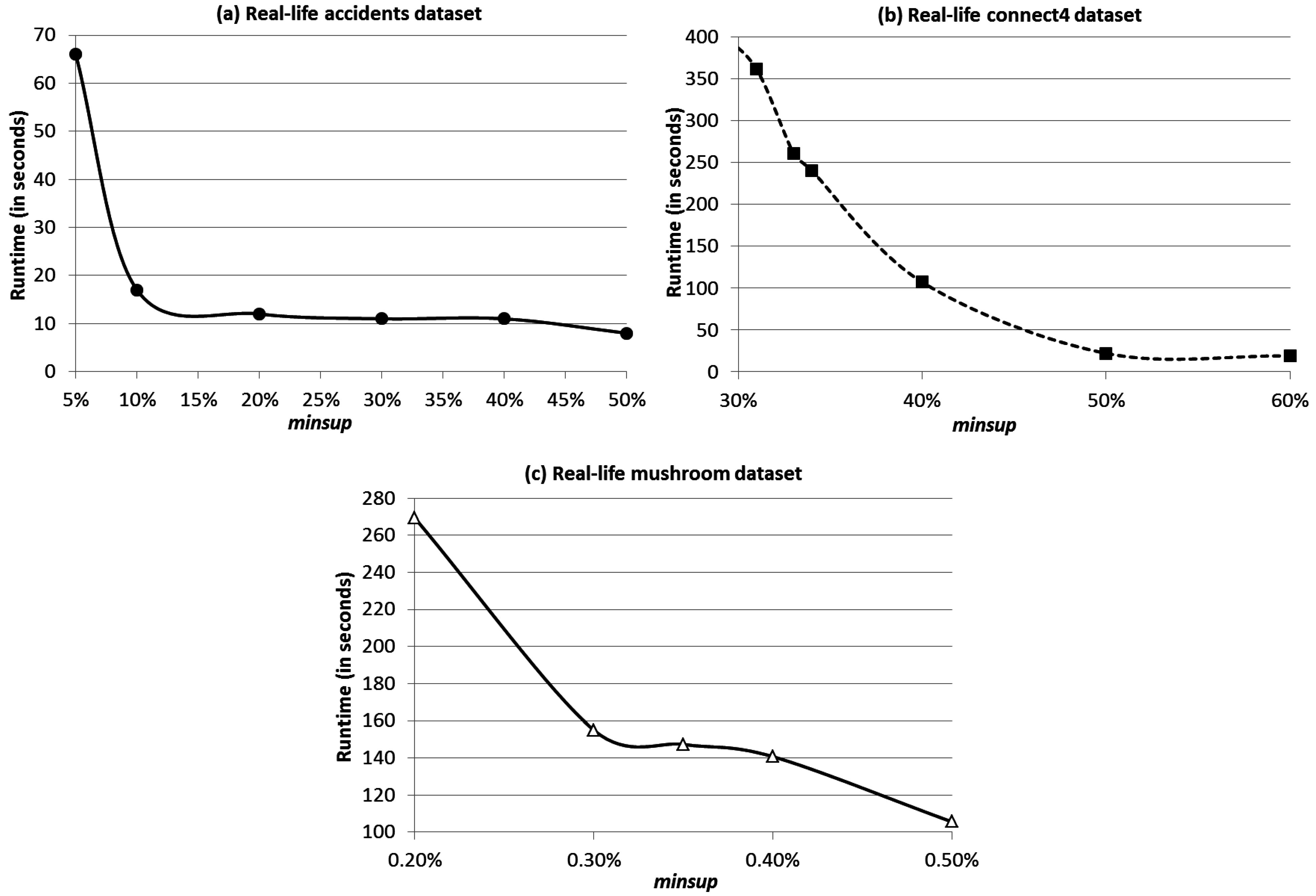
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cuzzocrea, A.; Saccà, D.; Ullman, J.D. Big Data: A Research Agenda. In Proceedings of the 17th International Database Engineering & Applications Symposium (IDEAS), Barcelona, Spain, 9–11 October 2013; pp. 198–203.
- Kejariwal, A. Big Data Challenges: A Program Optimization Perspective. In Proceedings of the Second International Conference on Cloud and Green Computing (CGC), Xiangtan, China, 1–3 November 2012; pp. 702–707.
- Madden, S. From Databases to Big Data. IEEE Int. Comput. 2012, 16, 4–6. [Google Scholar] [CrossRef]
- Cuzzocrea, A.; Bellatreche, L.; Song, I.-Y. Data Warehousing and OLAP over Big Data: Current Challenges and Future Research Directions. In Proceedings of the 16th International Workshop on Data Warehousing and OLAP (DOLAP), San Francisco, CA, USA, 28 October 2013; pp. 67–70.
- Jiang, F.; Kawagoe, K.; Leung, C.K. Big Social Network Mining for “Following” Patterns. In Proceedings of the Eighth International C* Conference on Computer Science & Software Engineering (C3S2E), Yokohama, Japan, 13–15 July 2015; pp. 28–37.
- Kawagoe, K.; Leung, C.K. Similarities of Frequent Following Patterns and Social Entities. Proced. Comput. Sci. 2015, 60, 642–651. [Google Scholar] [CrossRef]
- Leung, C.K.; Jiang, F. Big Data Analytics of Social Networks for the Discovery of “Following” Patterns. In Proceedings of the 17th International Conference on Big Data Analytics and Knowledge Discovery (DaWaK), Valencia, Spain, 1–4 September 2015; pp. 123–135.
- Ting, H.-F.; Lee, L.-K.; Chan, H.-L.; Lam, T.W. Approximating Frequent Items in Asynchronous Data Stream over a Sliding Window. Algorithms 2011, 4, 200–222. [Google Scholar] [CrossRef]
- Kumar, A.; Niu, F.; Ré, C. Hazy: Making It Easier to Build and Maintain Big-Data Analytics. Commun. ACM 2013, 56, 40–49. [Google Scholar] [CrossRef]
- Leung, C.K.; Hayduk, Y. Mining Frequent Patterns from Uncertain Data with MapReduce for Big Data Analytics. In Proceedings of the 18th International Conference on Database Systems for Advanced Applications (DASFAA), Part I, Wuhan, China, 22–25 April 2013; pp. 440–455.
- Leung, C.K.; Jiang, F. A Data Science Solution for Mining Interesting Patterns from Uncertain Big Data. In Proceedings of the IEEE Fourth International Conference on Big Data and Cloud Computing (BDCloud), Sydney, NSW, Australia, 3–5 December 2014; pp. 235–242.
- Leung, C.K.; MacKinnon, R.K. Reducing the Search Space for Big Data Mining for Interesting Patterns from Uncertain Data. In Proceedings of the 2014 IEEE International Congress on Big Data (BigData Congress), Anchorage, AK, USA, 27 June –2 July 2014; pp. 315–322.
- Dean, J.; Ghemawat, S. MapReduce: Simplified Data Processing on Large Clusters. Commun. ACM 2008, 51, 107–113. [Google Scholar] [CrossRef]
- Cuzzocrea, A.; Leung, C.K.; MacKinnon, R.K. Mining Constrained Frequent Itemsets from Distributed Uncertain Data. Future Generation Comput. Syst. 2014, 37, 117–126. [Google Scholar] [CrossRef]
- Leung, C.K.; MacKinnon, R.K.; Jiang, F. Distributed Uncertain Data Mining for Frequent Patterns Satisfying Anti-Monotonic Constraints. In Proceedings of the IEEE 28th International Conference on Advanced Information Networking and Applications (AINA) Workshops, Victoria, BC, Canada, 13–16 May 2014; pp. 1–6.
- Zaki, M.J. Parallel and Distributed Association Mining: A Survey. IEEE Concurr. 1999, 7, 14–25. [Google Scholar] [CrossRef]
- Ibrahim, A.; Jin, H.; Yassin, A.; Zou, D. Towards Privacy Preserving Mining over Distributed Cloud Databases. In Proceedings of the Second International Conference on Cloud and Green Computing (CGC), Xiangtan, China, 1–3 November 2012; pp. 130–136.
- Ismail, L.; Zhang, L. Modeling and Performance Analysis to Predict the Behavior of a Divisible Load Application in a Cloud Computing Environment. Algorithms 2012, 5, 289–303. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Y.; Xie, Y. Implementation of a Parallel Algorithm Based on a Spark Cloud Computing Platform. Algorithms 2015, 8, 407–414. [Google Scholar] [CrossRef]
- Alvi, A.K.; Zulkernine, M. A Natural Classification Scheme for Software Security Patterns. In Proceedings of the IEEE Ninth International Conference on Dependable, Autonomic and Secure Computing (DASC), Sydney, NSW, Australia, 12–14 December 2011; pp. 113–120.
- Meng, Q.; Kennedy, P.J. Determining the Number of Clusters in Co-Authorship Networks Using Social Network Theory. In Proceedings of the Second International Conference on Cloud and Green Computing (CGC), Xiangtan, China, 1–3 November 2012; pp. 337–343.
- Agrawal, R.; Srikant, R. Fast Algorithms for Mining Association Rules. In Proceedings of the 20th International Conference on Very Large Data Bases (VLDB), Santiago de Chile, Chile, 12–15 September 1994; pp. 487–499.
- Fariha, A.; Ahmed, C.F.; Leung, C.K.; Samiullah, M.; Pervin, S.; Cao, L. A New Framework for Mining Frequent Interaction Patterns from Meeting Databases. Eng. Appl. Artif. Intell. 2015, 45, 103–118. [Google Scholar] [CrossRef]
- Cameron, J.J.; Cuzzocrea, A.; Jiang, F.; Leung, C.K. Frequent Pattern Mining from Dense Graph Streams. In Proceedings of the Workshops of the EDBT/ICDT 2014 Joint Conference, Athens, Greece, 28 March 2014; pp. 240–247.
- Chorley, M.J.; Colombo, G.B.; Allen, S.M.; Whitaker, R.M. Visiting Patterns and Personality of Foursquare Users. In Proceedings of the IEEE Third International Conference on Cloud and Green Computing (CGC), Karlsruhe, Germany, 30 September–2 October 2013; pp. 271–276.
- Cuzzocrea, A.; Jiang, F.; Lee, W.; Leung, C.K. Efficient Frequent Itemset Mining from Dense Data Streams. In Proceedings of the 16th Asia-Pacific Web Conference (APWeb), Changsha, China, 5–7 September 2014; pp. 593–601.
- Cameron, J.J.; Leung, C.K. Mining Frequent Patterns from Precise and Uncertain Data. Comput. Syst. J. 2011, 1, 3–22. [Google Scholar]
- Cuzzocrea, A.; Furfaro, F.; Saccà, D. Hand-OLAP: A System for Delivering OLAP Services on Handheld Devices. In Proceedings of the Sixth International Symposium on Autonomous Decentralized Systems (ISADS), Pisa, Italy, 9–11 April 2003; pp. 80–87.
- Leung, C.K.; MacKinnon, R.K. Balancing Tree Size and Accuracy in Fast Mining of Uncertain Frequent Patterns. In Proceedings of the 17th International Conference on Big Data Analytics and Knowledge Discovery (DaWaK), Valencia, Spain, 1–4 September 2015; pp. 57–69.
- Tong, W.; Leung, C.K.; Liu, D.; Yu, J. Probabilistic Frequent Pattern Mining by PUH-Mine. In Proceedings of the 17th Asia-Pacific Web Conference (APWeb), Guangzhou, China, 18–20 September 2015; pp. 781–793.
- Tong, Y.; Chen, L.; Cheng, Y.; Yu, P.S. Mining Frequent Itemsets over Uncertain Databases. PVLDB 2012, 5, 1650–1661. [Google Scholar] [CrossRef]
- Leung, C.K.; Mateo, M.A.F.; Brajczuk, D.A. A Tree-Based Approach for Frequent Pattern Mining from Uncertain Data. In Proceedings of the 12th Pacific-Asia Conference on Knowledge Discovery and Data Mining (PAKDD), Osaka, Japan, 20–23 May 2008; pp. 653–661.
- Leung, C.K.; MacKinnon, R.K.; Tanbeer, S.K. Fast Algorithms for Frequent Itemset Mining from Uncertain Data. In Proceedings of the IEEE 14th International Conference on Data Mining (ICDM), Shenzhen, China, 14–17 December 2014; pp. 893–898.
- Leung, C.K.; MacKinnon, R.K. BLIMP: A Compact Tree Structure for Uncertain Frequent Pattern Mining. In Proceedings of the 16th International Conference on Data Warehousing and Knowledge Discovery (DaWaK), Munich, Germany, 2–4 September 2014; pp. 115–123.
- Ng, R.T.; Lakshmanan, L.V.S.; Han, J.; Pang, A. Exploratory Mining and Pruning Optimizations of Constrained Associations Rules. In Proceedings of the 1998 ACM SIGMOD International Conference on Management of Data, Seattle, WA, USA, 2–4 June 1998; pp. 13–24.
- Jiang, F.; Leung, C.K.; MacKinnon, R.K. BigSAM: Mining Interesting Patterns from Probabilistic Databases of Uncertain Big Data. In Proceedings of the PAKDD 2014 International Workshops, Tainan, Taiwan, 13–16 May 2014; pp. 780–792.
- Lin, M.-Y.; Lee, P.-Y.; Hsueh, S.-C. Apriori-Based Frequent Itemset Mining Algorithms on MapReduce. In Proceedings of the ACM Sixth International Conference on Ubiquitous Information Management and Communication (ICUIMC), Kuala Lumpur, Malaysia, 20–22 February 2012. [CrossRef]
- Riondato, M.; DeBrabant, J.; Fonseca, R.; Upfal, E. PARMA: A Parallel Randomized Algorithm for Approximate Association Rules Mining in MapReduce. In Proceedings of the ACM 21st International Conference on Information and Knowledge Management (CIKM), Maui, HI, USA, 29 October–2 November 2012; pp. 85–94.
- Lakshmanan, L.V.S.; Leung, C.K.; Ng, R.T. Efficient Dynamic Mining of Constrained Frequent Sets. ACM Trans. Database Syst. 2003, 28, 337–389. [Google Scholar] [CrossRef]
- Leung, C.K. Frequent Itemset Mining with Constraints. In Encyclopedia of Database Systems; Springer: New York, NY, USA, 2009; pp. 1179–1183. [Google Scholar]
- Leung, C.K. Uncertain Frequent Pattern Mining. In Frequent Pattern Mining; Springer International Publishing: Cham, Switzerland, 2014; pp. 417–453. [Google Scholar]
- Leung, C.K. Mining Frequent Itemsets from Probabilistic Datasets. In Proceedings of the Fifth International Conference on Emerging Databases (EDB), Jeju Island, South Korea, 19–21 August 2013; pp. 137–148.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, F.; Leung, C.K. A Data Analytic Algorithm for Managing, Querying, and Processing Uncertain Big Data in Cloud Environments. Algorithms 2015, 8, 1175-1194. https://0-doi-org.brum.beds.ac.uk/10.3390/a8041175
Jiang F, Leung CK. A Data Analytic Algorithm for Managing, Querying, and Processing Uncertain Big Data in Cloud Environments. Algorithms. 2015; 8(4):1175-1194. https://0-doi-org.brum.beds.ac.uk/10.3390/a8041175
Chicago/Turabian StyleJiang, Fan, and Carson K. Leung. 2015. "A Data Analytic Algorithm for Managing, Querying, and Processing Uncertain Big Data in Cloud Environments" Algorithms 8, no. 4: 1175-1194. https://0-doi-org.brum.beds.ac.uk/10.3390/a8041175






