Reweighted Factor Selection for SLMS-RL1 Algorithm under Gaussian Mixture Noise Environments
Abstract
:1. Introduction
2. Problem Formulation
2.1. Review of SLMS-RL1 Algorithm
2.2. Problem Formulation
3. Reweighted Factor Selection for SLMS-RL1 Algorithm
| Parameters | Values |
|---|---|
| Training signal structure | Pseudo-random Binary sequences |
| Channel length | |
| No. of nonzero coefficients | |
| Distribution of nonzero coefficient | Random Gaussian distribution |
| Received SNR | |
| GMM noise distribution | , , |
| Step-size | |
| Regularization parameters for sparse penalties | |
| Thresholds of the SLMS-RL1 algorithms |
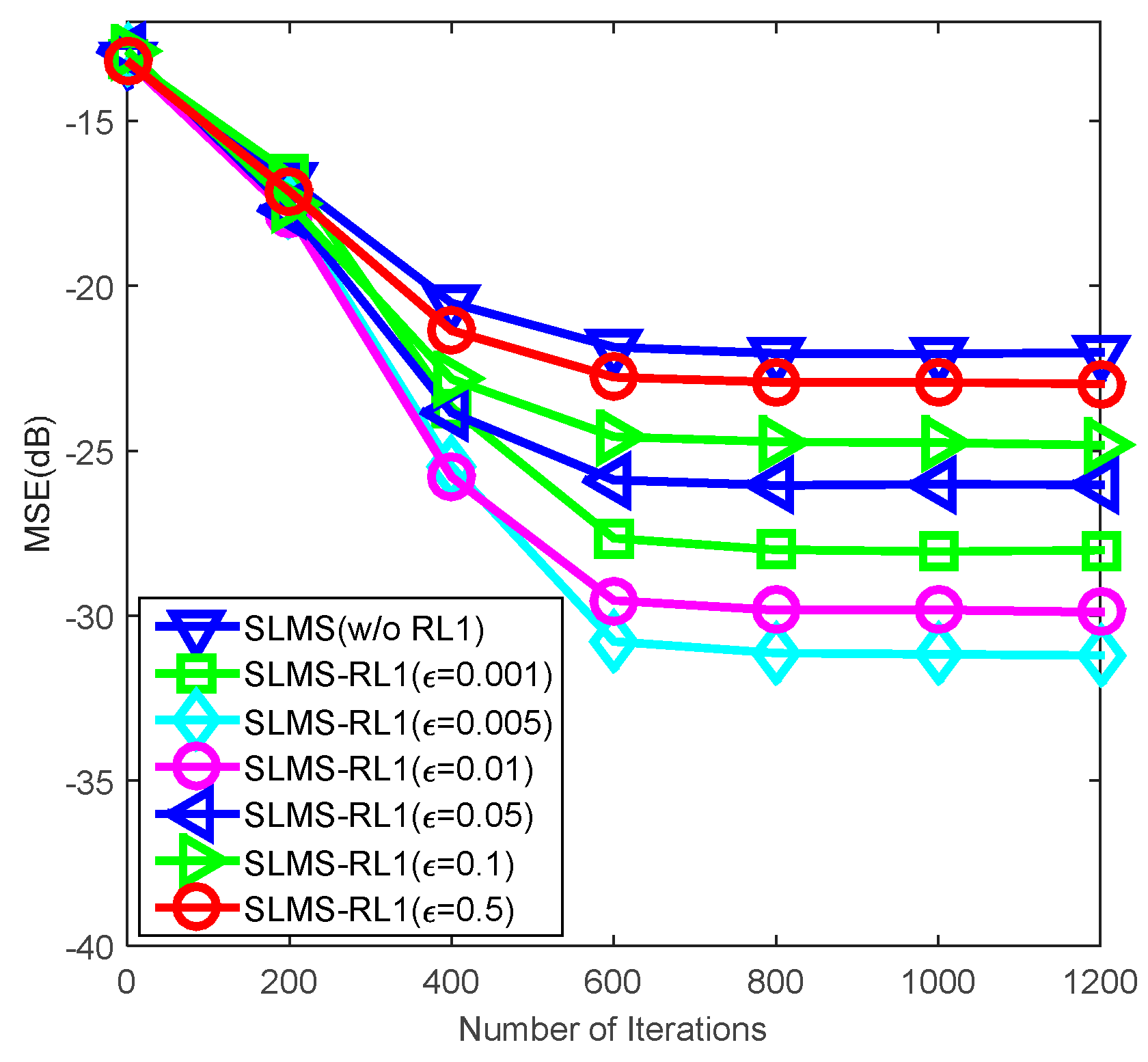
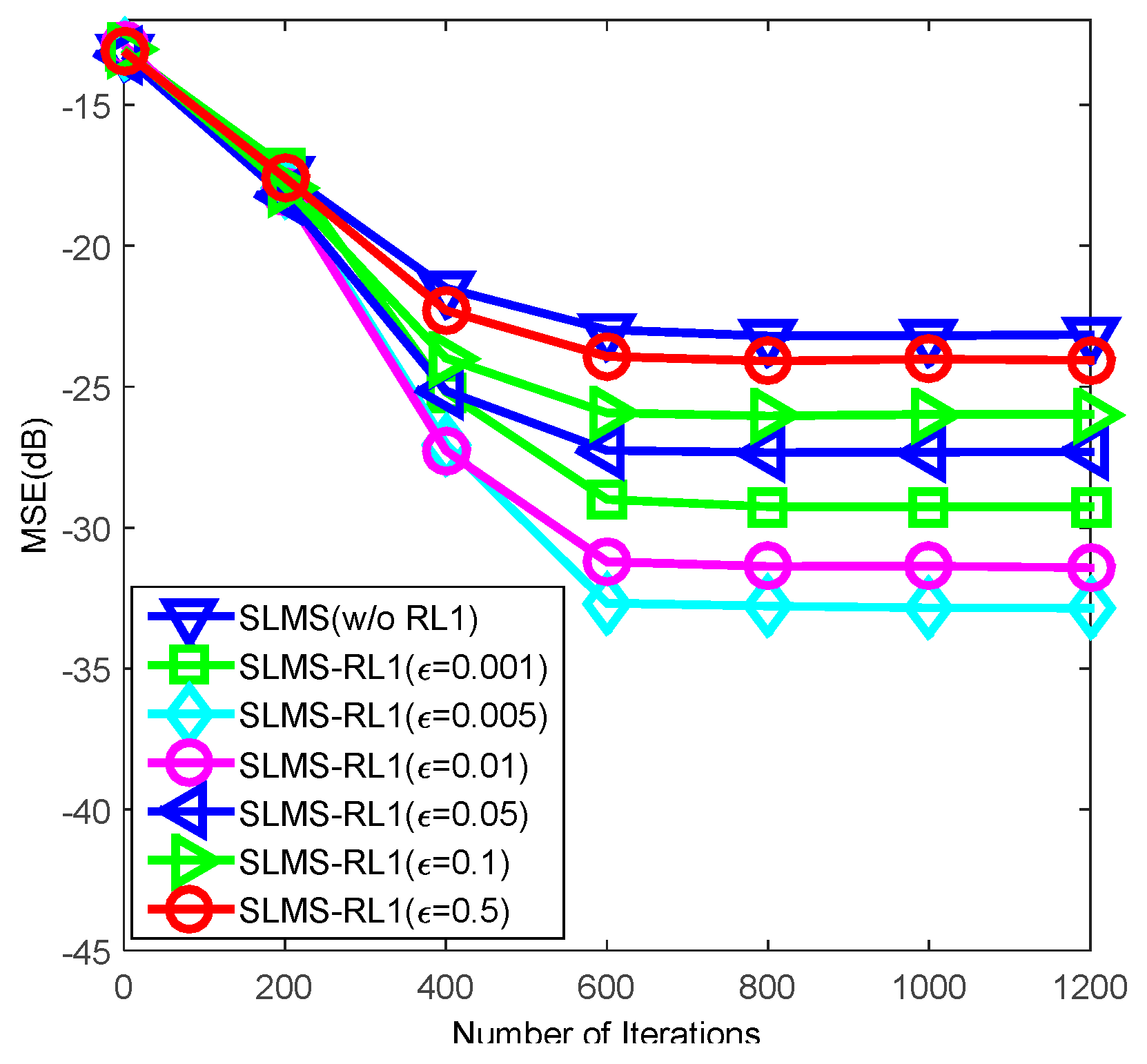
4. Numerical Simulations
| Parameters | Values |
|---|---|
| Training signal structure | Pseudo-random Binary sequences |
| Channel length | |
| No. of nonzero coefficients | |
| Distribution of nonzero coefficient | Random Gaussian distribution |
| Received SNR | |
| GMM noise distribution ( controls impulsive noise strength) | , , |
| Step-size | |
| Regularization parameters for sparse penalties | |
| Threshold of the SLMS-RL1 |


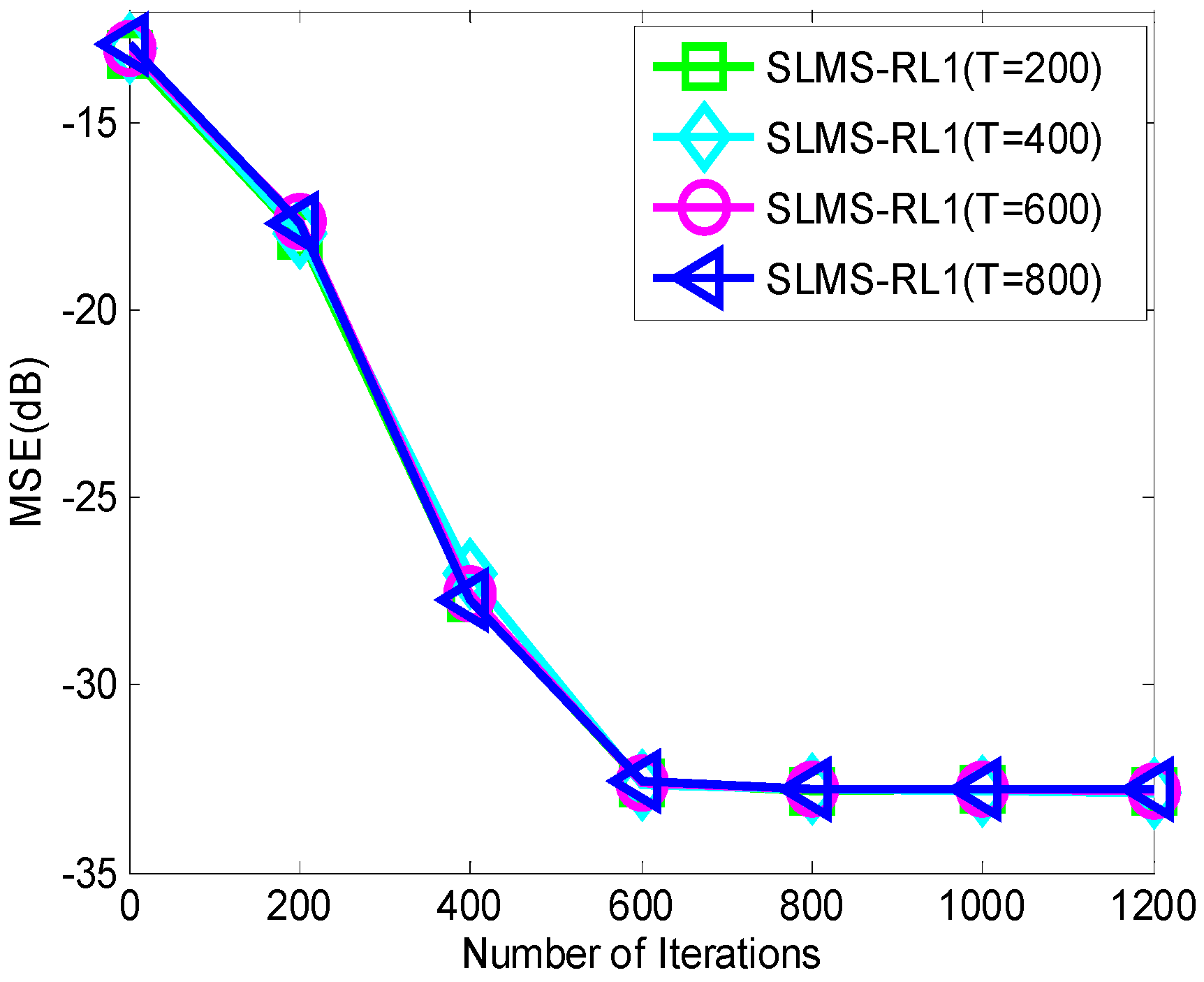
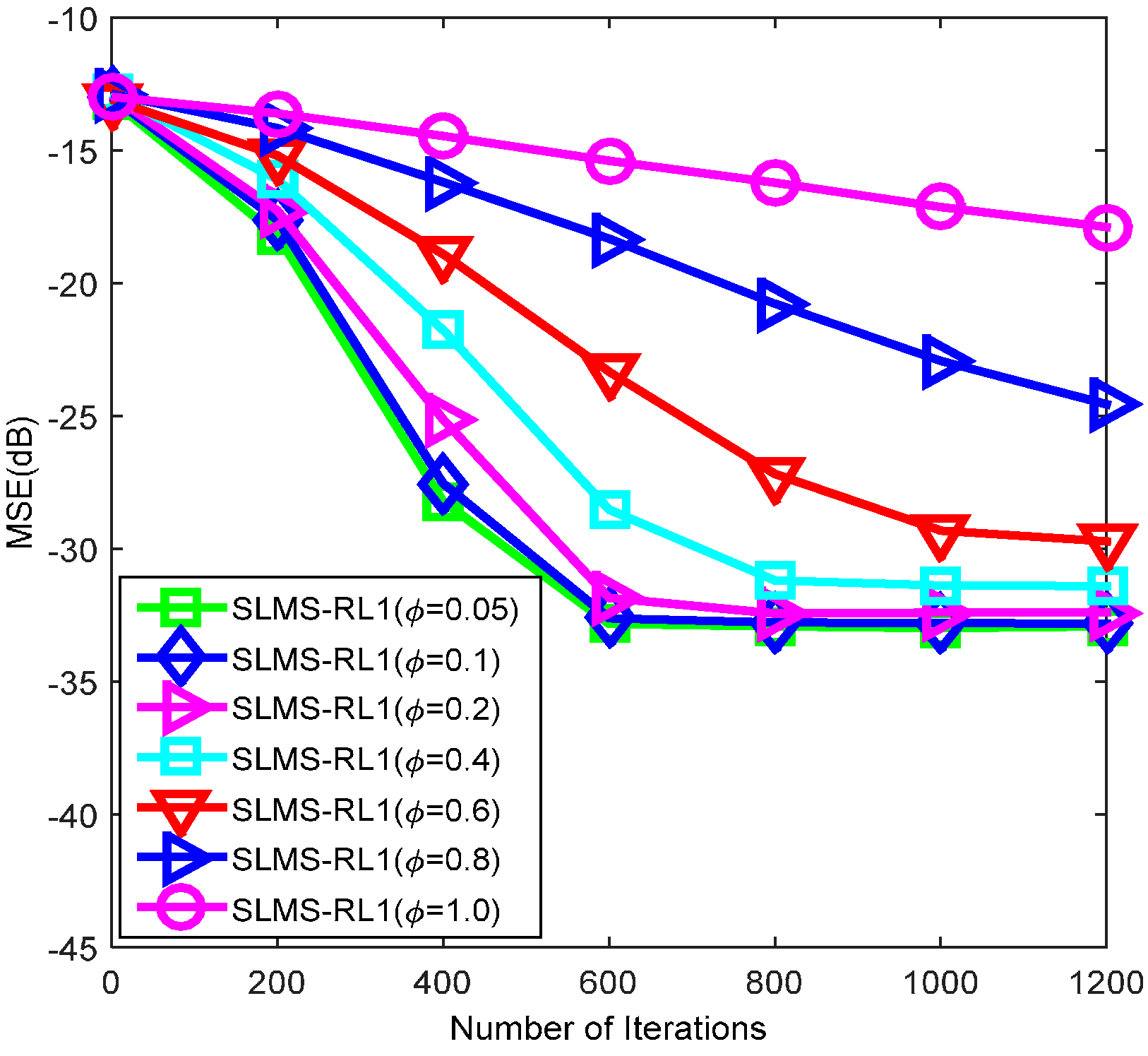
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sayed, A.H. Adaptive Filters; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Haykin, S.S. Adaptive Filter Theory, Prentice Hall, Upper Saddle River, NJ, USA, 1996.
- Yoo, J.; Shin, J.; Park, P. Variable step-size affine projection aign algorithm. IEEE Trans. Circuits Syst. Express Br. 2014, 61, 274–278. [Google Scholar]
- Chen, B.; Zhao, S.; Zhu, P.; Principe, J.C. Quantized kernel recursive least squares algorithm. IEEE Trans. Neural Netw. Learn. Syst. 2013, 24, 1484–1491. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Zhao, S.; Zhu, P.; Principe, J.C. Quantized kernel least mean square algorithm. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 22–32. [Google Scholar] [CrossRef] [PubMed]
- Taheri, O.; Vorobyov, S.A. Sparse channel estimation with LP-norm and reweighted L1-norm penalized least mean squares. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 2864–2867.
- Gendron, P.J. An empirical Bayes estimator for in-scale adaptive filtering. IEEE Trans. Signal Process. 2005, 53, 1670–1683. [Google Scholar] [CrossRef]
- Adachi, F.; Kudoh, E. New direction of broadband wireless technology. Wirel. Commun. Mob. Comput. 2007, 7, 969–983. [Google Scholar] [CrossRef]
- Raychaudhuri, B.D.; Mandayam, N.B. Frontiers of wireless and mobile communications. Proc. IEEE 2012, 100, 824–840. [Google Scholar] [CrossRef]
- Dai, L.; Wang, Z.; Yang, Z. Next-generation digital television terrestrial broadcasting systems: Key technologies and research trends. IEEE Commun. Mag. 2012, 50, 150–158. [Google Scholar] [CrossRef]
- Adachi, F.; Garg, D.; Takaoka, S.; Takeda, K. Broadband CDMA techniques. IEEE Wirel. Commun. 2005, 12, 8–18. [Google Scholar] [CrossRef]
- Shao, M.; Nikias, C.L. Signal processing with fractional lower order moments: Stable processes and their applications. Proc. IEEE 1993, 81, 986–1010. [Google Scholar] [CrossRef]
- Middleton, D. Non-Gaussian noise models in signal processing for telecommunications: New methods and results for class A and class B noise models. IEEE Trans. Inf. Theory 1999, 45, 1129–1149. [Google Scholar] [CrossRef]
- Jiang, X.; Zeng, W.-J.; So, H.C.; Rajan, S.; Kirubarajan, T. Robust matched filtering in lp-space. IEEE Trans. Signal Process. Unpublished work. 2015. [Google Scholar] [CrossRef]
- Gao, Z.; Dai, L.; Lu, Z.; Yuen, C.; Member, S.; Wang, Z. Super-resolution sparse MIMO-OFDM channel estimation based on spatial and temporal correlations. IEEE Commun. Lett. 2014, 18, 1266–1269. [Google Scholar] [CrossRef]
- Dai, L.; Wang, Z.; Yang, Z. Compressive sensing based time domain synchronous OFDM transmission for vehicular communications. IEEE J. Sel. Areas Commun. 2013, 31, 460–469. [Google Scholar]
- Qi, C.; Wu, L. Optimized pilot placement for sparse channel estimation in OFDM systems. IEEE Signal Process. Lett. 2011, 18, 749–752. [Google Scholar] [CrossRef]
- Gui, G.; Peng, W.; Adachi, F. Sub-Nyquist rate ADC sampling-based compressive channel estimation. Wirel. Commun. Mob. Comput. 2015, 15, 639–648. [Google Scholar] [CrossRef]
- Gui, G.; Zheng, N.; Wang, N.; Mehbodniya, A.; Adachi, F. Compressive estimation of cluster-sparse channels. Prog. Electromagn. Res. C 2011, 24, 251–263. [Google Scholar] [CrossRef]
- Jiang, X.; Kirubarajan, T.; Zeng, W.-J. Robust sparse channel estimation and equalization in impulsive noise using linear programming. Signal Process. 2013, 93, 1095–1105. [Google Scholar] [CrossRef]
- Jiang, X.; Kirubarajan, T.; Zeng, W.J. Robust time-delay estimation in impulsive noise using lp-correlation. In Proceedings of the IEEE Radar Conference (RADAR), Ottawa, ON, Canada, 29 April–3 May 2013; pp. 1–4.
- Lin, J.; Member, S.; Nassar, M.; Evans, B.L. Impulsive noise mitigation in powerline communications using sparse Bayesian learning. IEEE J. Sel. Areas Commun. 2013, 31, 1172–1183. [Google Scholar] [CrossRef]
- Zhang, T.; Gui, G. IMAC: Impulsive-mitigation adaptive sparse channel estimation based on Gaussian-mixture model. Available online: http//arxiv.org/abs/1503.00800 (accessed on 14 September 2015).
- Candes, E.J.; Wakin, M.B.; Boyd, S.P. Enhancing sparsity by reweighted L1 minimization. J. Fourier Anal. Appl. 2008, 14, 877–905. [Google Scholar] [CrossRef]
- Bajwa, W.U.; Haupt, J.; Sayeed, A.M.; Nowak, R. Compressed channel sensing: A new approach to estimating sparse multipath channels. Proc. IEEE 2010, 98, 1058–1076. [Google Scholar] [CrossRef]
- Tauböck, G.; Hlawatsch, F.; Eiwen, D.; Rauhut, H. Compressive estimation of doubly selective channels in multicarrier systems: Leakage effects and sparsity-enhancing processing. IEEE J. Sel. Top. Signal Process. 2010, 4, 255–271. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, T.; Gui, G. Reweighted Factor Selection for SLMS-RL1 Algorithm under Gaussian Mixture Noise Environments. Algorithms 2015, 8, 799-809. https://0-doi-org.brum.beds.ac.uk/10.3390/a8040799
Zhang T, Gui G. Reweighted Factor Selection for SLMS-RL1 Algorithm under Gaussian Mixture Noise Environments. Algorithms. 2015; 8(4):799-809. https://0-doi-org.brum.beds.ac.uk/10.3390/a8040799
Chicago/Turabian StyleZhang, Tingping, and Guan Gui. 2015. "Reweighted Factor Selection for SLMS-RL1 Algorithm under Gaussian Mixture Noise Environments" Algorithms 8, no. 4: 799-809. https://0-doi-org.brum.beds.ac.uk/10.3390/a8040799





