1. Introduction
A chemical equation is only a symbolic representation of a chemical reaction and represents an expression of atoms, elements, compounds or ions. Such expressions are generated based on balancing through reactant or product coefficients, as well as through reactant or product molar masses [
1]. In fact, equilibrating the equations that represent the stoichiometry of a reacting system is a matter of mathematics, since it can be reduced to the problem of solving homogeneous linear systems.
Balancing chemical equations is an important application of generalized inverses. To discuss further, the reflexive
g-inverse of a matrix has been successfully used in solving a general problem of balancing chemical equations (see [
2,
3]). Continuing in the same direction, Krishnamurthy in [
4] gave a mathematical method for balancing chemical equations founded by virtue of a generalized matrix inverse. The method used in [
4] is based on the exact computation of reflexive generalized inverses by means of elementary matrix transformations and the finite-field residue arithmetic, as it was described in [
5].
It is well known that the symbolic data processing, including both rational arithmetic and multiple modulus residue arithmetic, are time consuming, both for the implementation and for execution. On the other hand, the finite-field exact arithmetic is inapplicable to chemical reactions, which include atoms with fractional and/or integer oxidation numbers. This hard class of chemical reactions is investigated in [
6].
Additionally, the balancing chemical equations problem can be readily resolved by computer algebra software, as was discussed in [
7]. The approach used in [
7] is based on the usage of the Gaussian elimination (also known as the Gauss–Jordan algorithm), while the approach that is exploited in [
2] is based on singular value decomposition (SVD). On the other hand, it is widely known that Gaussian elimination, as well as SVD require a large amount of numerical operations [
8]. Furthermore, small pivots that could appear in Gaussian elimination can lead to large multipliers [
9], which can sometimes lead to the divergence of numerical algorithms. Two methods of balancing chemical equations, introduced in [
10], are based on integer linear programming and integer nonlinear programming models, respectively. Notice that the linear Diophantine matrix method was proposed in [
11]. The method is applicable in cases when the reaction matrices lead to infinite stoichiometrically-independent solutions.
In the present paper, we consider the possibility of applying a new higher order iterative method for computing the Moore–Penrose inverse in the problem of balancing chemical equations. In general, our current research represents the first attempt to apply iterative methods in balancing chemical reactions.
A rapid numerical algorithm for computing matrix-generalized inverses with a prescribed range and null space is developed in order to implement this global idea. The method is based on an appropriate modification of the hyper-power iterative method. Furthermore, some techniques for the acceleration of the method in the initial phase of its convergence is discussed. We also try to show the applicability of proposed iterative schemes in balancing chemical equations. Before a more detailed discussion, we briefly review some of the important backgrounds incorporated in our work.
The outer inverse with prescribed range
T and null space
S of a matrix
, denoted by
, satisfies the second Penrose matrix equation
and two additional properties:
and
. The significance of these inverses is reflected primarily in the fact that the most important generalized inverses are particular cases of outer inverses with a prescribed range and null space. For example, the Moore–Penrose inverse
, the weighted Moore–Penrose inverse
, the Drazin inverse
and the group inverse
can be derived by means of the appropriate choices of subspaces
T and
S in what follows:
wherein
and
denotes the index of a square matrix
A (see, e.g., [
12]).
Although there are many approaches to calculate these inverses by means of direct methods, an alternative and very important approach is to use iterative methods. Among many such matrix iterative methods, the hyper-power iterative family has been introduced and investigated (see, for example, [
13,
14,
15]). The hyper-power iteration of the order
p is defined by the following scheme (see, for example, [
13]):
The iteration Equation (
2) requires
p matrix-matrix multiplications (from now on denoted by mmm) to achieve the
p-th order of convergence. The adoption
yields to the Schulz matrix iteration, originated in [
16],
with the second rate of convergence. Further, choice
gives the cubically-convergent method of Chebyshev [
17], defined as follows:
For more details about the background of iterative methods for computing generalized inverses, please refer to [
18].
The main motivation of the paper [
19] was the observation that the inverse of the reaction matrix cannot always be obtained. For this purpose, the author used an approach based on row-reduced echelon forms of both the reaction matrix and its transpose. Since the Moore–Penrose inverse always exists, replacement of the ordinary inverse by the corresponding pseudoinverse resolves the drawback that the inverse of the reaction matrix does not always exist. Furthermore, two successive transformations into the corresponding row-reduced echelon forms are time-consuming and badly-conditioned numerical processes, again based on Gaussian elimination. Our intention is to avoid the above-mentioned drawbacks that appear in previously-used approaches.
Here, we decide to develop an application of the Schulz-type methods. The motivation is based on the following advantages arising from the use of these methods. Firstly, they are totally applicable on sparse matrices possessing sparse inverses. Secondly, the Schulz-type methods are useful for providing approximate inverse preconditions. Thirdly, such schemes are parallelizable, while Gaussian elimination with partial pivoting is not suitable for the parallelism.
It is worth mentioning that an application of iterative methods in finding exact solutions that involve integers or rational entries requires an additional transformation of the solution and utilization of tools for symbolic data processing. To this end, we used the programming package Mathematica.
The rest of this paper is organized as follows. A new formulation of a very high order method is presented in
Section 2. The method is fast and economical at the same time, which is confirmed by the fact that it attains a very high rate of convergence by using a relatively small number of mmm. Acceleration of the convergence via scaling the initial iterates is discussed, and some novel approaches in this trend are given in the same section. An application of iterative methods in balancing chemical equations is considered in
Section 3. A comparison of numerical results obtained by applying the introduced method is shown against the results defined by using several similar methods. Some numerical experiments concerning the application of the new iterations in balancing chemical equations are presented in
Section 4. Finally, some concluding remarks are drawn in the last section.
2. An Efficient Method and Its Acceleration
A Schulz-type method of high order with two improvements is derived and chosen as one of the options for balancing chemical equations. The first improvement is based on a proper factorization, which reduces the number of mmm required in each cycle. The second straightening is based on a proper accelerating of initial iterations.
Toward this goal, we consider Equation (
2) in the case
as follows:
In its original form, the hyper-power iteration Equation (
5) is of the order 31 and requires 31 mmm. It is necessary to remark that a kind of effectiveness of a computational iterative (fixed point-type) method can be estimated by the real number (called the computational efficiency index)
, wherein
θ and
p stand for the whole computational cost and the rate of convergence per cycle, respectively. Here, the most important burden and cost per cycle is the number of matrix-matrix products.
Clearly, in Equation (
5), this proportion between the order of convergence and the needed number of mmm is not suitable, since its efficiency index:
is relatively small. This shows that Equation (
5) is not a useful iterative method. To improve the applicability of Equation (
5) and, so, to derive a fast matrix iteration with a reduced number of mmm,
i.e., to obtain an efficient method, we keep going as in the following subsection.
2.1. An Efficient Method
We rewrite Equation (
5) as:
Subsequently, Equation (
7) results in the following formulation of Equation (
5):
Now, we could deduce our final fast matrix iteration by simplifying Equation (
8) more:
where only nine mmm are required. Therefore, the efficiency index of the proposed fast iterative method becomes:
The efficiency index
of Equation (
9) is higher than the efficiency index 1.4142 of Equation (
3), higher than the efficiency index 1.4422 of Equation (
4) and finally higher than the efficiency index 1.4592 of the 30th order method proposed recently by Sharifi
et al. [
20].
At this point, it would be useful to provide the following theorem regarding the convergence behavior of Equation (
9).
Theorem 1. Let be a given matrix of rank r and be a given matrix of rank , which satisfy . Then, the sequence generated by the iterative method Equation (
9)
converges to with 31st-order if the initial approximation satisfies: Proof. The proof of this theorem would be similar to the ones in [
21]. Hence, we skip it over and just include the following error bound:
wherein
. ☐
The derived iterative method is very fast and effective, in contrast to the existing iterative Schulz-type methods of the same type. However, as was pointed out by Soleimani
et al. [
22], such iterative methods are slow at the beginning of the iterative process, and the real convergence rate cannot be observed. An idea to remedy this disadvantage is to apply a multiple root-finding algorithm on the matrix equation
and to try to accelerate the hyper-power method in its initial iterations. Such a discussion about a scaled version of the hyper-power method is the main aim of the next subsection.
2.2. Accelerating the Initial Phase
Another useful motivation of the present paper is processed here. The iterative scheme:
was applied in [
22] to achieve the convergence phase in the main (modified Householder) method much more rapidly and to accelerate the beginning of the process. In the second iteration phase, it is sufficient to apply the introduced fast and efficient modified Householder method, which then reaches its own full speed of convergence [
22].
In the same vein, the iterative expression Equation (
13) can be rewritten in the following equivalent, but more practical form:
One can now observe that Equation (
14) is the particular case (
) of the following new scheme:
Therefore, Equation (
15) can be considered as an important acceleration of the Schulz-type method Equation (
2) in the initial phase, before the convergence rate is practically achievable. We note that such accelerations are useful for large matrices, whereas the iterative methods require too much iterations to converge. Particularly, by following Equation (
15), one can immediately notice that the accelerating in the initial phase of iteration Equation (
9) is of the form:
Remark 1. The particular choice in Equation (
15)
reduces these iterations to the usual hyper-power family of the iterative methods possessing the order :The choice in Equation (
15)
leads to the scaled Schulz matrix iteration considered recently in [23], and the choice , produces the original Schulz matrix iteration, originated in [12]. Finally, a hybrid algorithm may be written now by incorporating Equations (
9) and (
16) as follows.
| Algorithm 1 The new hybrid method for computing generalized inverses. |
- 1:
The input is given - 2:
Use Equation ( 16) until (for an inner loop counter l or ). - 3:
set - 4:
for until convergence ( ), use Equation ( 9) to converge with high order. - 5:
end for
|
Instead of the hybrid Algorithm 1, based on the usage of Equation (
16) in the initial phase and Equation (
9) in the final stage, our third result here is to define a unique iterative method, which can be derived by applying variable acceleration parameter
,
. This approach yields scaled hyper-power iterations of the general form:
where the initial approximation
is chosen according to Equation (
11).
Furthermore, it is possible to propose various modifications of
in a manner that guarantees
. For example:
3. Balancing Chemical Equations Using Iterations
In accordance with the intention that was motivated in the first section, in this section, we investigate the applicability of some iterations from the hyper-power family in balancing chemical equations. It is shown that the iterative methods can be applied successfully without any limitations.
It is assumed that a chemical system is modeled by a single reaction of the general form (see, for example, [
2]):
In Equation (
20),
(resp.
) are unknown rational coefficients of the reactants (resp. the products),
,
are chemical elements in reactants and products, respectively, and
and
are the numbers of atoms
and
, respectively, in the
j-th molecule.
3.1. Balancing Chemical Equations Using Iterative Methods
The coefficients
are integers, rational or real numbers, which should be determined on the basis of three basic principles: (1) the law of conservation of mass; (2) the law of conservation of atoms; (3) the time-independence of Equation (
20), an assumption usually valid for stable/non-sensitive reactions. Let there be
m distinct atoms involved in the chemical reaction Equation (
20) and
distinct reactants and products. It is necessary to form an
matrix
A, called the reaction matrix, whose columns represent the reactants and products and the rows represent the distinct atoms in the chemical reaction. More precisely, the
-th element of
A, denoted by
, represents the number of atoms of type
i in each compound/element (reactant or product). An arbitrary element
is positive or negative according to whether it corresponds to a reactant or a product. Hence, the balancing chemical equation problem can be formulated as the homogeneous matrix equation:
with respect to the unknown vector
, where
denotes the reaction matrix and 0 denotes the null column vector of the order
m. In this way, an arbitrary chemical reaction can be formulated as a matrix equation.
We would like to use the symbolic and numerical possibilities of the Mathematica computer algebra system in conjunction with the above-defined iterative method(s) for computing generalized inverses to automatize the chemical reactions balancing process.
The general solution of the balancing problem in the matrix form Equation (
21) is given by:
where
c is the arbitrarily-selected
n-dimensional vector. Let us assume that the approximation of
generated by an arbitrary iterative method is given by
.
If the iterative method for computing
X is performed in the floating point arithmetic, it is necessary to perform a transition from the solution whose coordinates are real numbers into an exact (integer and/or rational) solution. Thus, the iterative approach in balancing chemical equations assumes three general algorithmic steps, as is described in Algorithm 2.
| Algorithm 2 General algorithm for balancing chemical equations by an iterative solver. |
- 1:
Apply (for example) Algorithm 1 and compute the approximation of . - 2:
Compute the vector s using Equation ( 22). - 3:
Transform real numbers included in s into an exact solution.
|
A clear observation about Algorithms 2 is the following:
- -
Steps 1 and 2 require usage of real arithmetic (with very high precision);
- -
Step 3 requires usage of symbolic processing and exact arithmetic capabilities to deal with rational numbers.
As a result, in order to apply iterative methods to the problem of balancing chemical equations, it is necessary to use a software that meets two diametrically-opposite criteria: the ability to carry out numerical calculations (with very high precision) and the ability to apply the exact arithmetic and symbolic calculations. The programming language
Mathematica possesses both of these properties. More details about this programming language can be found in [
24].
The following (sample)
Mathematica code can be used to determine the exact solution using real values contained in the vector
s (defined in Equation (
22)).
Id = IdentityMatrix[n]; s = (Id - X.A).ConstantArray[1, n];
s = Rationalize[s, 10^(-300)]; c = s*LCM @@ Denominator /@ s;
(* Multiply s by the Least Common Multiple of denominators in s *)
s = c/Min @@ Numerator /@ c
(* Divide c by the Minimum of numerators in c *)
The standard Mathematica function Rationalize[x,dx] yields the rational number with the smallest denominator within a given tolerance of x. Sometimes, to avoid the influence of round-off errors and possible errors caused by the usage of the function Rationalize, it is necessary to perform iterative steps with a very high precision.
An improvement of the vector s can be attained as follows. It is possible to propose an amplification of the vector , where c is an n-dimensional column vector. The improvement can be obtained using . In the practical implementation, it is necessary to replace the expression s = (Id - X.A).ConstantArray[1, n] by s = (Id - X.A).((Id - X.A).ConstantArray[1, n]).
This replacement can be explained by the fact that is closer to the zero vector zero than .
3.2. Balancing Chemical Equations in Symbolic Form
As was explained in [
6], balancing
ℵ chemical reactions that possess atoms with fractional oxidation numbers and non-unique coefficients is an extremely hard problem in chemistry. The case when the system Equation (
21) is not uniquely determined can be resolved using the
Mathematica function
Reduce. If a
ℵ chemical reaction includes
n reaction molecules and
m reaction elements, then the reaction matrix
A is of the order
. In the case
, the reaction has
general solutions. All of them can be found applying the following expression:
where the zero vector in the right-hand side is of the length
m and
is the list of dependent variables.
4. Experimental Results
Let us denote the iterations Equation (
3) by NM (Newton’s Method), the iterations Equation (
4) by CM (Chebyshev’s Method) and Equation (
9) by PM (Proposed Method). Here, we apply different methods in the Mathematica 10 environment to compute some generalized inverses and to show the superiority of our scheme(s). We also denote the hybrid algorithm given in [
22] by HAL (Householder Algorithm) and our Algorithm 1 is denoted by APM (Accelerated Proposed Method). Throughout the paper the computer characteristics are Microsoft Windows XP Intel(R), Pentium(R) 4 CPU, 3.20 GHz with 4 GB of RAM, unless stated otherwise (as in the end of Example 1).
4.1. Numerical Experiments on Randomly-Generated Matrices
Example 1. [22] In this numerical experiment, we compute the Moore–Penrose inverse of a dense, randomly-generated matrix, which is defined as follows: The numerical results corresponding to the number of iterations and the CPU time are illustrated in
Table 1, wherein IT denotes the number of iterative steps. It shows that APM with
and five inner loops, while
, is superior to the other existing methods. We employed HAL with
and eight inner loops. Note that the initial matrix is chosen as
, while the stopping criterion is defined by
. Here,
stands for the Frobenius norm (Hilbert–Schmidt norm), which is for an
matrix
A defined as:
where
denotes the conjugate transpose of
A,
are the singular values of
A and the trace function is used.
Table 1.
The results corresponding to the Moore–Penrose inverse of a randomly-generated matrix. IT, number of iterative steps.
Table 1.
The results corresponding to the Moore–Penrose inverse of a randomly-generated matrix. IT, number of iterative steps.
| Methods | NM | CM | HAL | APM |
|---|
| IT | 28 | 18 | 14 | 9 |
| Time | 15.7656250 | 15.0000000 | 14.0156250 | 13.4687500 |
It is important to emphasize that the computational time is directly initiated by computer and software specifications. To clarify this, we execute our implemented algorithms/methods from Example 1 on a more recently-featured computer, whose characteristics are Windows 7 Ultimate, Intel(R) Core(TM) i5-4400 CPU 3.10 GHz with 8 GB of RAM and 64 Operating System. The results corresponding to this hardware/software configuration are given in
Table 2 in terms of the elapsed CPU time. Furthermore, we re-ran Example 1 for an
matrix, which was randomly generated by the code:
to show that our schemes can also simply be applied on matrices satisfying
. The results generated by these values are arranged in
Table 3, where
inner loops are considered for APM.
Table 2.
The results corresponding to the Moore–Penrose inverse of randomly-generated matrices with a better equipped computer.
Table 2.
The results corresponding to the Moore–Penrose inverse of randomly-generated matrices with a better equipped computer.
| Methods | NM | CM | HAL | APM |
|---|
| Time | 1.620093 | 1.570090 | 1.363078 | 1.279073 |
Table 3.
The results corresponding to the Moore–Penrose inverse of the randomly-generated matrix .
Table 3.
The results corresponding to the Moore–Penrose inverse of the randomly-generated matrix .
| Methods | NM | CM | HAL | APM |
|---|
| IT | 28 | 18 | 14 | 8 |
| Time | 2.714405 | 2.605205 | 2.371204 | 2.293204 |
The numerical example illustrates the theoretical results presented in
Section 2. It can be observed from the results included in
Table 1,
Table 2 and
Table 3 that, firstly, like the existing methods, the presented method shows a stable behavior along with a fast convergence. Additionally, according to results contained in
Table 1,
Table 2 and
Table 3, it is clear that the number of iterations required in the APM method during numerical approximations of the Moore–Penrose inverse is smaller than the number of approximations generated by the classical methods. This observation is in accordance with the fact that the efficiency index is clearly the largest in the case of the APM method. In general, APM is superior among all of the existing famous hyper-power iterative schemes. This superiority is in accordance with the theory of efficiency analysis discussed before.
In fact, it can be observed that increasing the efficiency index by a proper factorization of the hyper-power method is a kind of nice strategy that gives promising results in terms of both the number of iterations and the computational time on different computers.
Here, it is also worth noting that Schulz-type solvers are the best choice for sparse matrices possessing sparse inverses. Since, in such cases, the usual SVD technique in the software, such as Mathematica or MATLAB, ruins the sparsity pattern and requires much more time, hence such iterative methods and the SVD-type (direct) schemes are both competitive, but have their own fields of applications.
4.2. Numerical Experiments in Balancing Chemical Equations
In this subsection, we present some clear examples indicating the applicability of our approach in the balancing chemical equations. We also apply the following initial matrix .
Example 2. Consider a specific skeletal chemical equation from [10]:where the left-hand side of the arrow consists of compounds/elements called reactants, while the right-hand side comprises compounds/elements called the products. Hence, Equation (
24)
is formulated as the homogeneous equation , wherein 0 denotes the null column vector and: The results generated after the comparison of numerical results derived in Example 2 are given in Table 4, using 300 precision digits, being large enough to minimize round-off errors, as well as to clearly observe the computed asymptotic error constants in the convergence phase. Although in all practical problems, the machine precision (double precision) is enough (just like Example (1)), here, our focus is to find very accurate coefficients for the chemical equation, since a very accurate tolerance, such as ,
must be incorporated. The final exact coefficients are defined as
. Thus,
Experimental results clearly show that PM is the most efficient method for this purpose. In addition, we remark that since we use iterative methods in floating point arithmetic to obtain the coefficient, we must use the command in the last lines of our written Mathematica code, so as to attain the coefficients in exact arithmetic.
Table 4.
The results corresponding to balancing Equation (
24).
Table 4.
The results corresponding to balancing Equation (24).
| Methods | NM | CM | PM |
|---|
| IT | 14 | 9 | 3 |
| | | |
In order to support the improvement described in
Section 3, it is worth mentioning that (using Mathematica notations):
and
Example 3. Now, we solve the following skeletal chemical equation from [10]: Equation (
27)
is formulated as a homogeneous system of linear equations with the following coefficient matrix: The results of this experiment generated by using the ordinary double precision arithmetic and the stopping termination are illustrated in Figure 1. Note that the final coefficients obtained in exact arithmetic are equal to .
The results once again show that PM is the best iterative process.
Figure 1.
Convergence history for different methods used in Example 3.
Figure 1.
Convergence history for different methods used in Example 3.
Example 4. Consider the following example from [19]: The reaction matrix A can be derived by taking into account both the law of conservation of atoms and the law of electrical neutrality, and it is equal to (see [
19]
): As in the previous examples, let us denote by X the result derived by the iterative method Equation (
9).
The rational approximation of is equal to , and the exact solution coincides with the result given in [19]: . Example 5. In this example, it is shown that our iterative method is capable of producing the solution in the case when the real coefficients are used and the reaction is not unique within relative proportions. Let us consider Reaction 1 with one arbitrary element from [6]: The reaction matrix of the homogeneous system Equation (
21)
is given by . The iterative method Equation (
9)
converges quickly, since the list of consecutive errors is given by , The approximate solution is equal to: and its fractional approximation is: Example 6. All possible solutions of the problem considered in Example 5 with respect to and can be generated using the Mathematica function Reduce:
Reduce[A.{{x1}, {x2}, {x3}, {x4}, {x5}} == {0, 0}, {x1, x2}
All solutions in the symbolic form are given as follows (using Mathematica notations):wherein are arbitrary real quantities. All possible solutions with respect to and can be generated using: Reduce[A.{{x1}, {x2}, {x3}, {x4}, {x5}} == {0, 0}, {x1, x3}]
All possible cases can be solved in the same way.
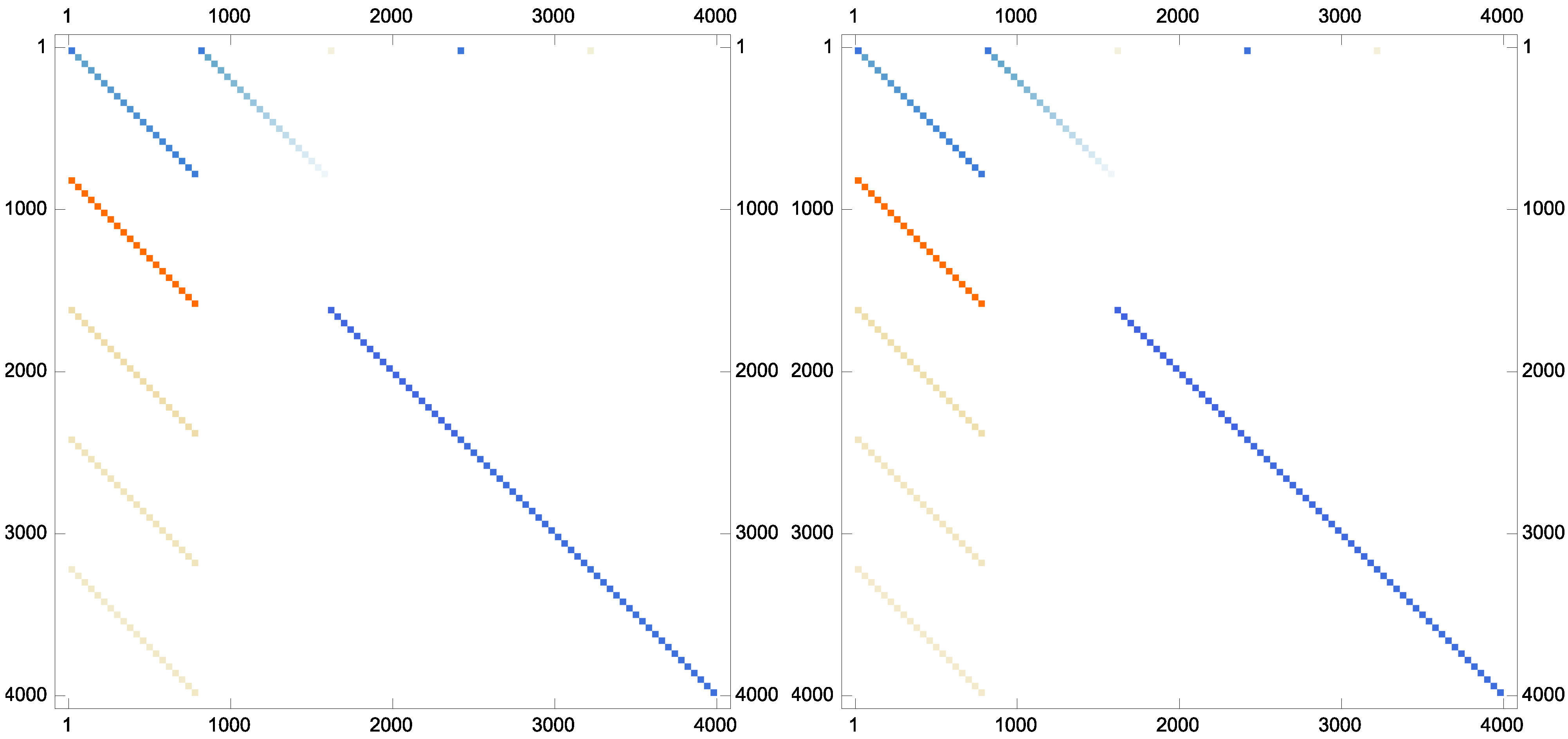
Example 7. As the last experiment and to show that the proposed iteration could preserve the sparsity pattern of the inverses if the inverses are sparse in nature, the following matrix has been taken from Matrix Market database with the stopping termination . The new scheme Equation (9) converges in twelve iterations. The matrix plots of the approximate inverse for this case are brought forward in Figure 2.
Figure 2.
The sparsity pattern for the approximate inverses: (top left); (top right); (bottom left); and (bottom right).
Figure 2.
The sparsity pattern for the approximate inverses: (top left); (top right); (bottom left); and (bottom right).