In the following sections, we present plane sweep and flow techniques for solving the one-dimensional separation problem.
6.1. The Plane Sweep Method
In order to solve the one-dimensional separation problem, we first define a partial order of all objects in the drawing (nodes, edges and labels). Then, we insert enough extra columns (horizontal space) between consecutive objects in the partial order, such that these objects are separated. Finally, we perform a compaction step in the drawing.
The task of defining the partial order of the objects in the drawing is not trivial, since an optimal partial order will produce an optimal solution for the OSLP problem. Recall that the input drawing is a planar or planarized graph. For each label, we define the following:
If a label overlaps more than one face of the drawing, then we place the label in the face where it overlaps the minimum area of other objects. An example is shown in
Figure 8, where the label belongs to edge (2, 5), but it can be placed either to the left or to the right of edge (2, 5). The face to the left of edge (2, 5) is the preferred face to place the label since it is wider than the face to the right of edge (2, 5). Furthermore, as is shown in
Figure 9, labels that overlap the boundaries of the face that they belong to are retracted inside that face.
A label is associated with one edge segment, in the case where an edge is composed of more than one segment. For example, in
Figure 10, the label belongs to edge
, which consists of the consecutive edge segments
,
,
,
and
. Since we cannot change the
y-coordinates of a label, the label can be either associated with the edge segment
or
.
Before we assign the partial order of labels, we decide if we will resolve overlaps by increasing the width or height of the drawing. Actually, in some cases, overlaps can be resolved only by increasing the height (width) of the drawing. For example, in
Figure 8, we have to increase the width, and in
Figure 9, we have to increase the height in order to resolve label overlaps. In other cases, as shown in
Figure 11 and
Figure 12, we could increase the width or height of the drawing. Usually, we increase the height (respectively width) when labels have a greater overlap in the horizontal (vertical) direction.
Because we consider the case where we resolve label overlaps by increasing only the width of the drawing, we take into account only those labels that will become overlap-free by increasing the width of the drawing.
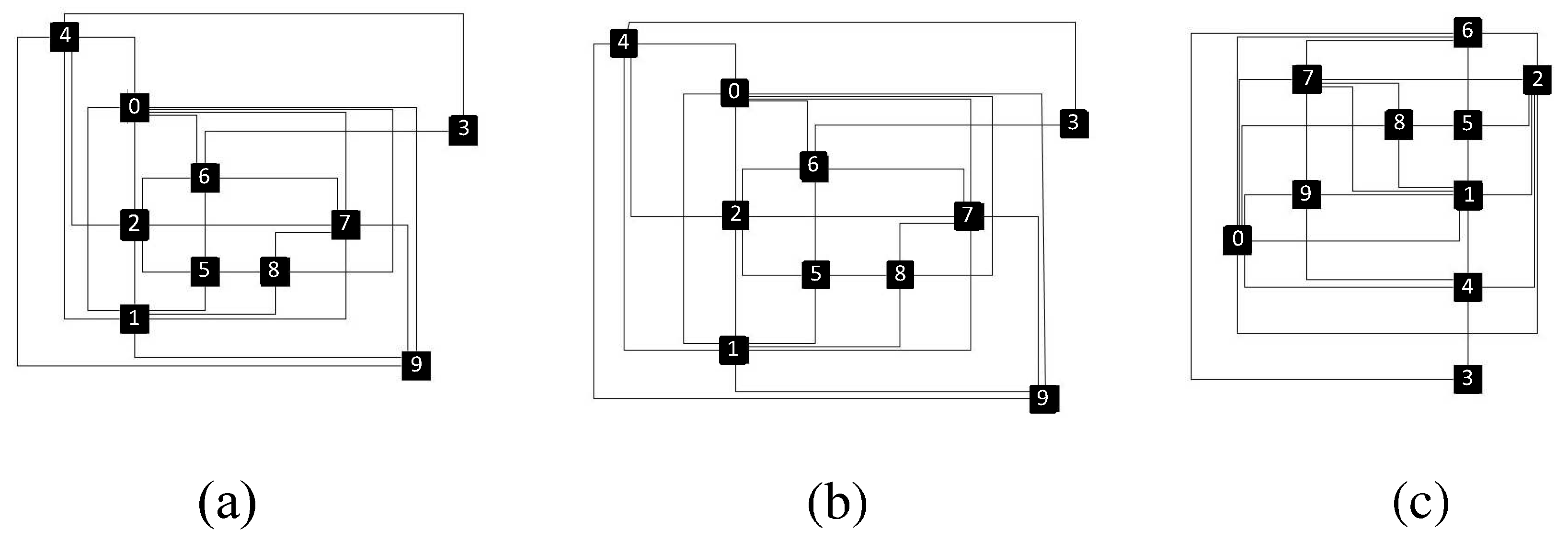
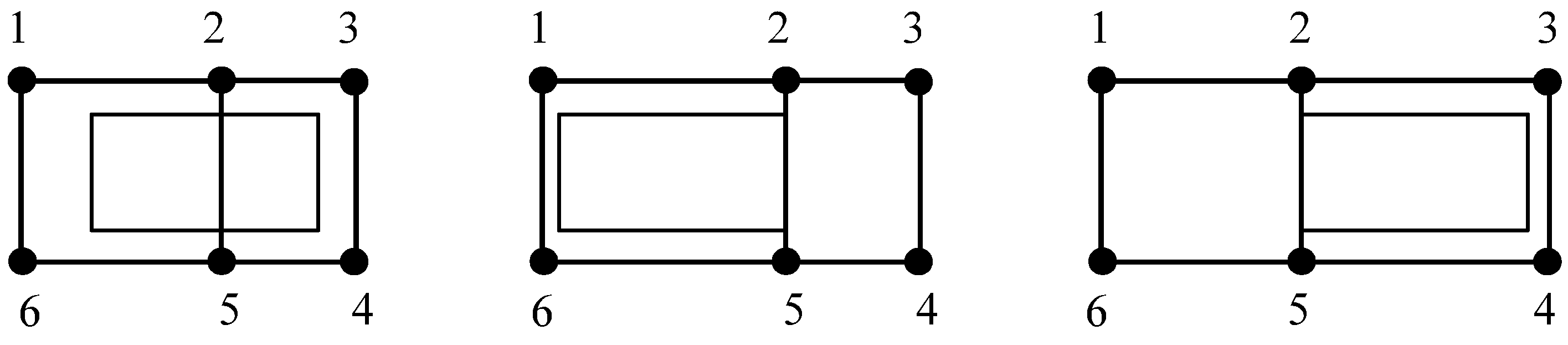
Now, we can assign the partial order of labels, nodes and vertical edge segments of the drawing. First, we associate each label with a vertical line segment (e.g., the left or right vertical side of the rectangle corresponding to the label). Then, we group nodes and vertical edge segments that are connected and share the same column in the drawing into single vertical objects, in order to preserve the orthogonal representation of the drawing; see
Figure 13. Next, we sweep the plane from left to right, and each time we encounter a vertical object for the first time, we place it at the end of a queue. The order in which we have placed each object in the queue reveals its position in the partial order. Note that a label to the right of its associated vertical edge goes after the edge into the queue.
Now, we perform a plane sweep of the drawing from left to right with a vertical line. Each time the sweep line touches a vertical segment corresponding to a label l, we insert columns to separate l from all objects to the right of the sweep line (i.e., we push to the right all objects that follow l in the partial order). By doing that, we ensure that we have eliminated all overlaps.
Note that we expand to the right all horizontal lines that the sweep line intersects. Furthermore, if a label is between two vertical edge segments connected to the same node, then we cannot insert columns to resolve overlaps, since the columns will stretch the node. Thus, we must move this label into a different position, in a preprocessing step, where we can resolve overlaps by expanding the drawing.
One could improve the partial order of overlapping labels by rearranging their order. For example, as shown in
Figure 12, different partial orders of overlapping labels produce different paths for the vertical space to be propagated through the drawing. Thus, in order to have efficient reuse of the vertical space inserted to resolve the overlaps, we place the top label, such that it has the minimum overlaps with other labels.
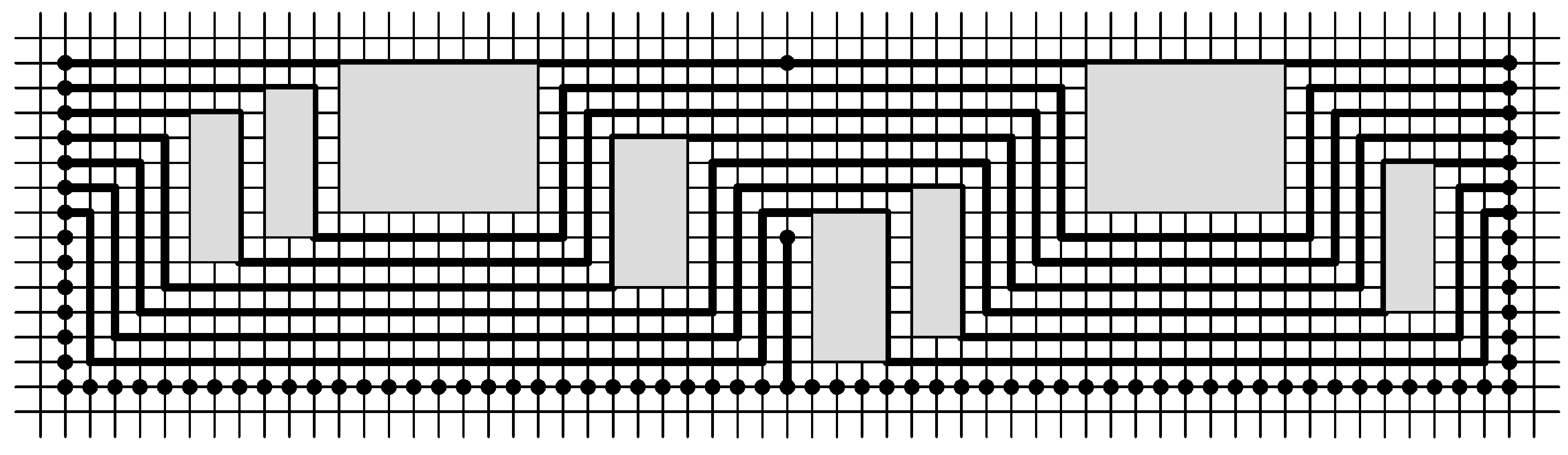
We have resolved overlaps by inserting extra columns between labels. It is easy to see that we could improve the solution by performing a VLSI compaction on the resulting drawing to minimize the width of the drawing; see
Figure 18. Actually, by the plane sweep method, we have transformed the one-dimensional separation problem to its equivalent one-dimensional VLSI compaction problem. There are efficient techniques that optimally solve the one-dimensional VLSI compaction (
i.e., compaction in one direction for objects with a predefined partial order) in polynomial time [
16,
17,
18]. These techniques are based on the longest path method. It is trivial to conclude that the plane sweep algorithm runs in
time, where
n is the number of vertices,
k is the number of vertical edge segments of the orthogonal representation and
l is the number of edge labels.
One weak point of the longest path method is that it has the tendency to push all objects towards one side. Thus, it produces not only drawings that have long edges, but also drawings that are very dense on one side, while space on the other side remains unused. This characteristic of the graph-based approach is acceptable in VLSI layout where legibility or aesthetics are not important considerations. However, in graph drawing, the aesthetic quality of a drawing is critical; thus, we must preserve the mental map of the drawing after inserting extra space to resolve label overlaps. Therefore, the above technique, even though it is very attractive since it is fast and simple, might not serve our purpose well after all. In the next section, we present a method that produces not only minimum width, but also minimum edge length and evenly-spaced drawings based on flow techniques.
6.2. The Flow Method
In this section, we use minimum flow techniques to find the minimum width needed to eliminate label overlaps in an orthogonal drawing Γ, given a partial order of overlapping objects, while preserving the orthogonal representation of Γ. The case of finding minimum height is analogous.
Generally speaking, we will create a directed acyclic graph that transfers flow from the top to the bottom of the drawing in order to insert extra vertical space to resolve horizontal overlaps. Intuitively, if two objects overlap, then we must push between them at least as much flow as the amount of their overlap in the x-direction. We create a digraph that captures all possible routes that we can push flow such that all horizontal overlaps are resolved.
Since we want to preserve the orthogonal representation of the drawing, we insert space in such a way that the path of the inserted space does not intersect any vertical edge segment. It is important to note that the space opened at the top of the drawing can be reused by objects below, and the goal is to maximize the reuse of the space.
First, we decompose the input drawing into vertical edge segments, nodes and labels. Next, we remove all horizontal edge segments. Then, we group nodes and edge segments that are connected and share the same column in the drawing into single vertical objects, in order to preserve the orthogonal representation of the drawing.
Next, we obtain the partial order of the objects (vertical objects, nodes and labels) in the decomposed drawing. Then, we create a special graph, which we call the separation visibility graph . We will use a plane sweep method similar to the one described in the previous section to find the partial order of the objects. We sweep the plane from left to right, and each time, we encounter an object for the first time we place it at the end of a queue. The order in which we have placed each object in the queue reveals its position in the partial order. Note that a label to the right of its associated vertical edge goes after the edge into the queue.
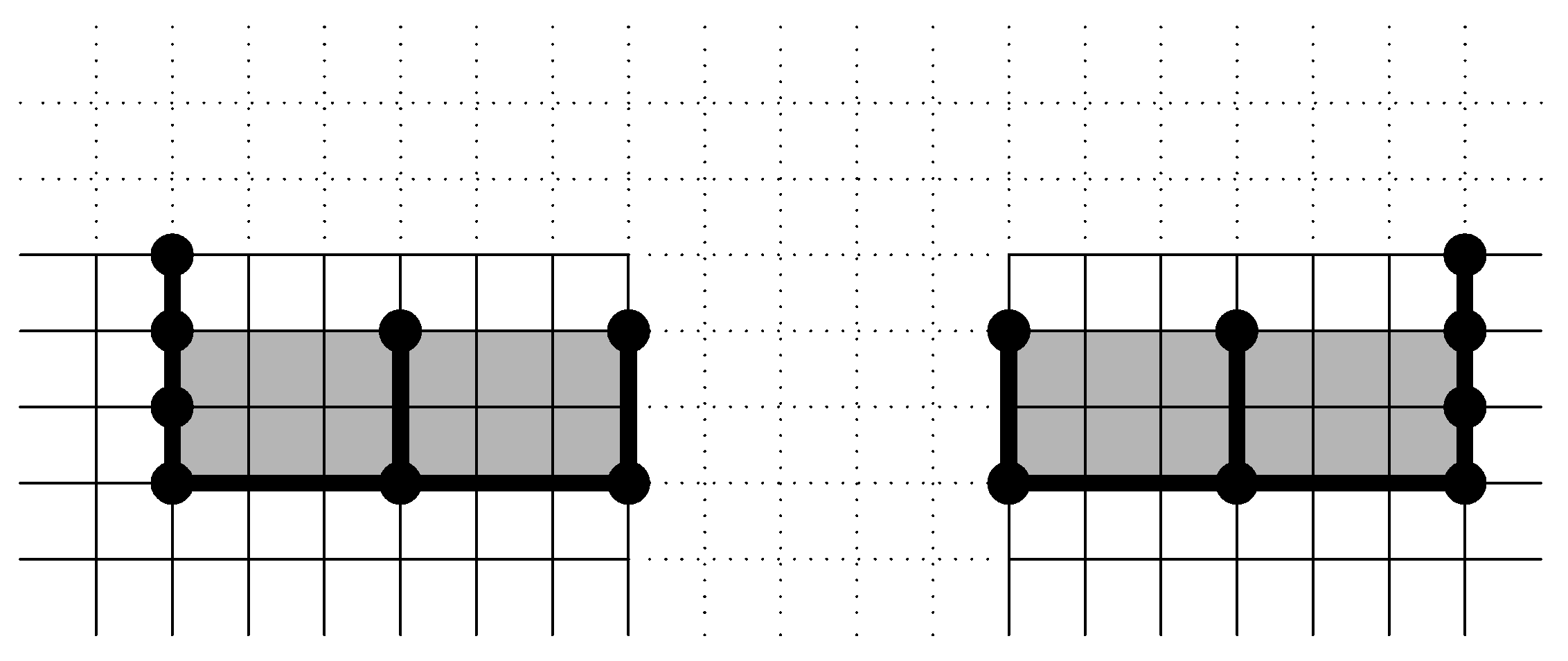
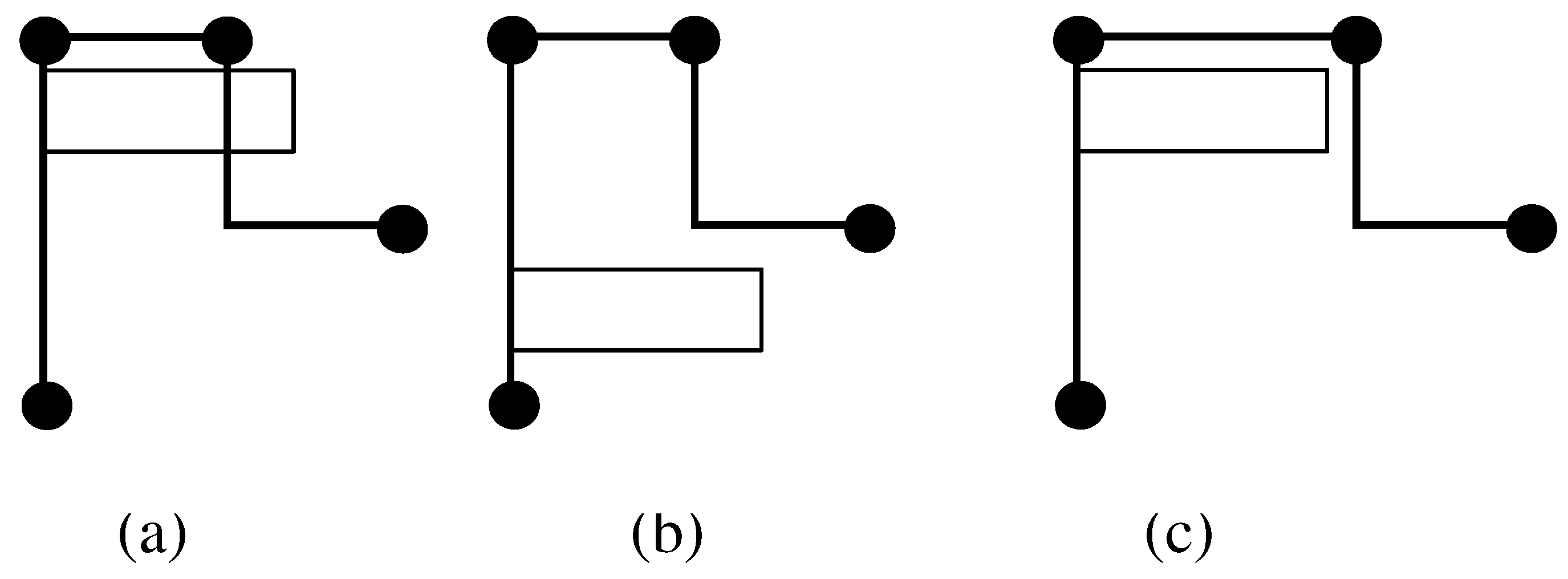
Then, we construct the separation visibility graph as follows: For each vertical segment and node of the decomposed input drawing, we insert a node in . For each edge label l, which is a rectangle, we insert two nodes and two horizontal edges in . The nodes correspond to the vertical sides of l and the edges to the horizontal sides of l. Next, we insert edges in by expanding (to the left and to the right) the horizontal sides of each node in until they touch another node of .
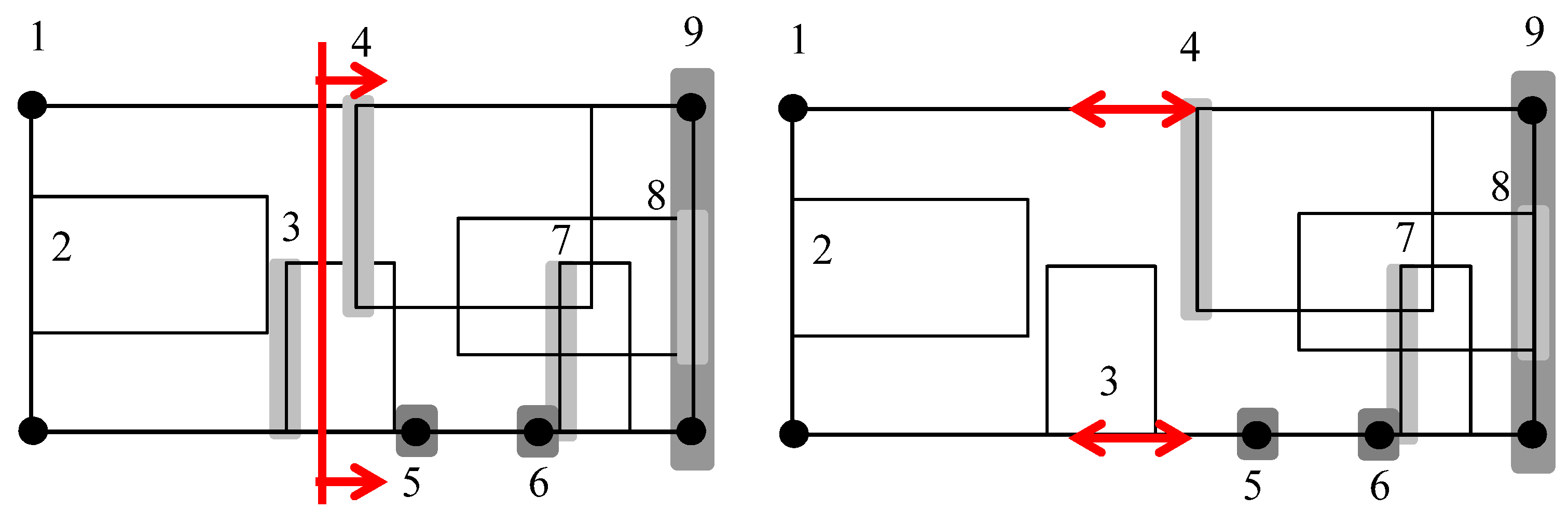
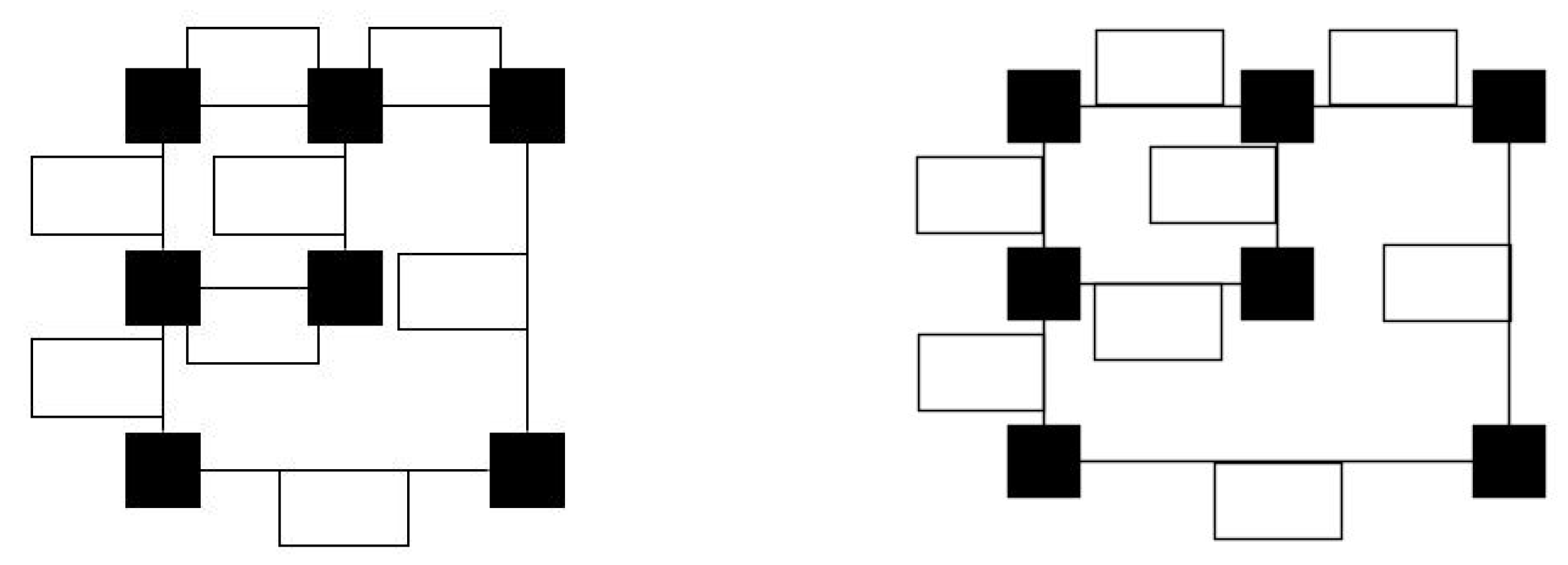
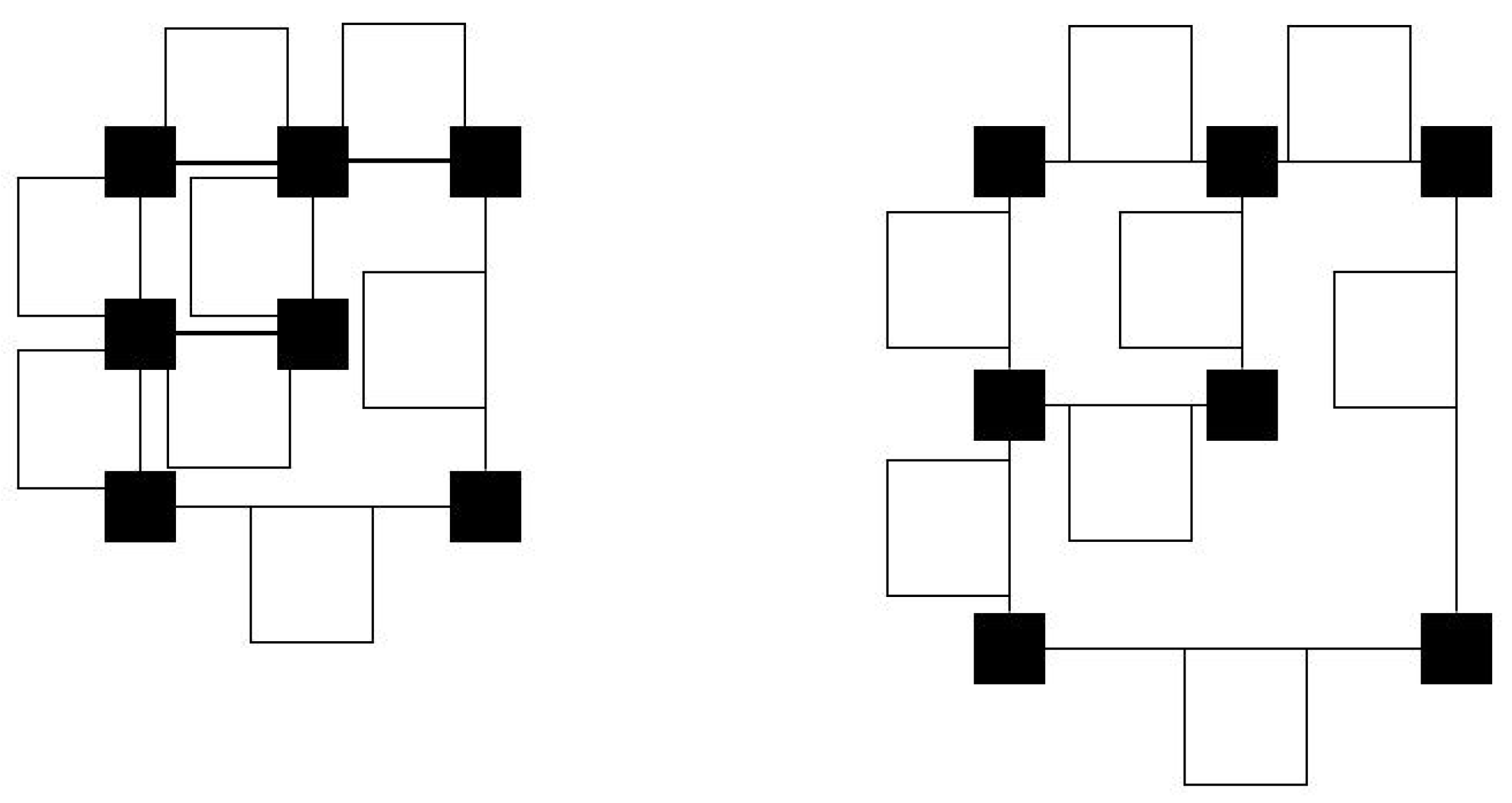
Figure 19a illustrates the ordered set of objects corresponding to the input drawing with overlapping labels shown in
Figure 13a. The corresponding separation visibility graph is shown in
Figure 19b. Notice that we add two vertical line segments (nodes in
), one to the left and one to the right of the set of ordered objects. By adding these two objects, we ensure that each face of the separation visibility graph is a rectangle.
Fact 2. Each face of the separation visibility graph is a rectangle.
We assign a weight to each edge
e of
, which represents the minimum distance the two objects connected with edge
e must be kept apart to avoid overlaps. We assign weights in the following fashion:
Each edge that connects two overlapping objects has weight equal to the amount of overlapping between these objects in the x-direction plus one.
Each edge that corresponds to a horizontal side of a rectangle that represents either a label or a node has weight equal to the width of that label or node.
Each edge that connects an edge e of the original drawing to a label assigned to e has weight zero.
Any other edge has weight one.
Next, we show how to create the graph
from the separation visibility graph
(see
Figure 20):
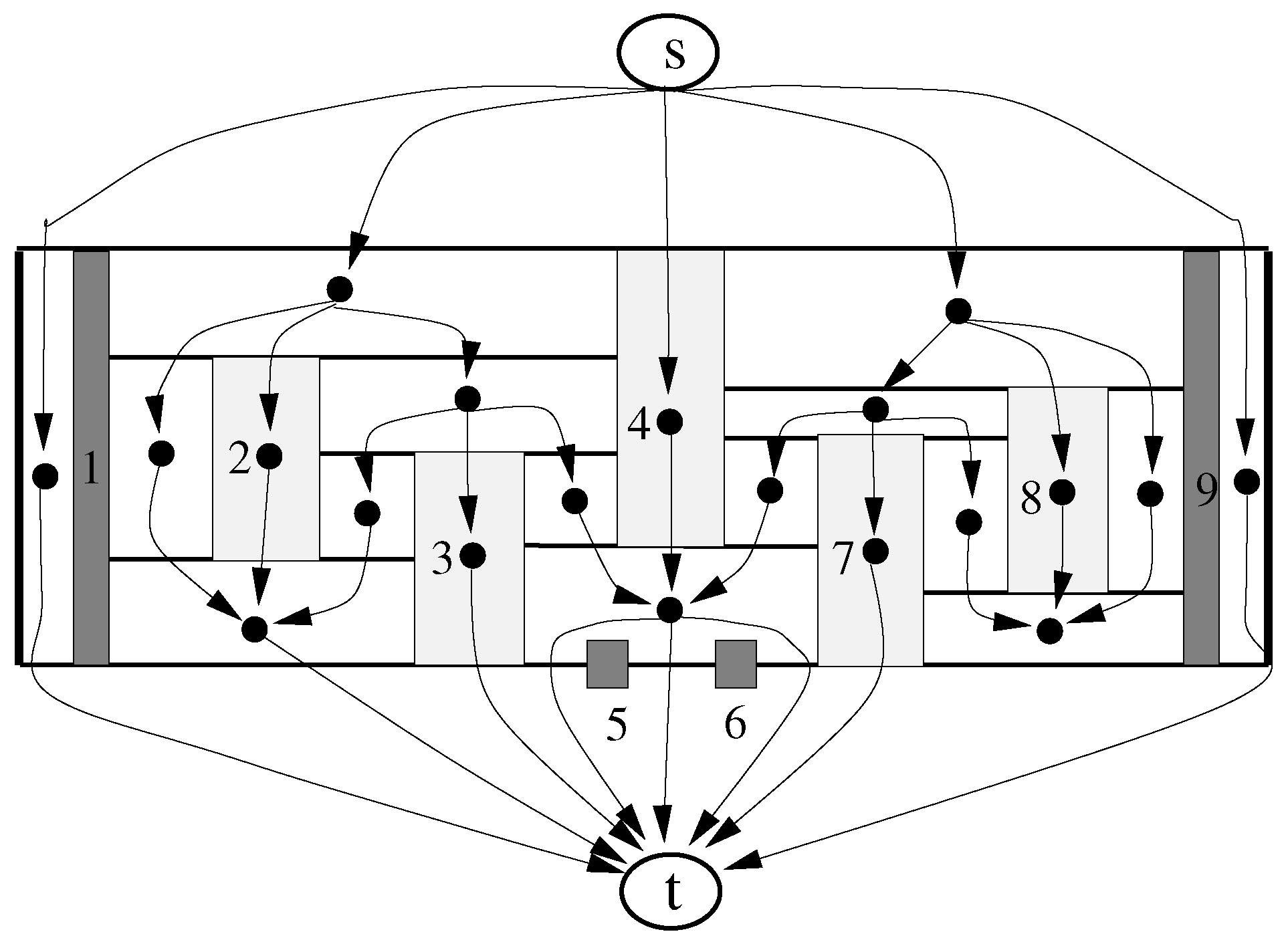
Insert into nodes s and t above and below, respectively, of .
Insert into a node for each face of .
Add edges into that connect two neighboring faces of that share a horizontal edge segment. Edges are directed towards the face with a smaller y-coordinate.
Connect with edges node s to each face that has a horizontal segment visible from a horizontal line that intersects node s.
Connect with edges each face that has a horizontal segment visible from a horizontal line that intersects node t to node t.
By the construction of the separation visibility graph and Fact 2 we can prove the following result:
Lemma 1. Graph includes every possible path that can be used to open up space in the x-direction to resolve overlaps without changing the orthogonal representation of the input orthogonal drawing.
In order to find the minimum width needed to resolve overlaps, we assign a lower and upper capacity to each edge of
. Notice that each edge in
intersects an edge in the corresponding
graph. Each edge in
has lower and upper capacity equal to a pair of weights for the only edge in
that intersects. We obtain the pair of weights for each edge in
as follows:
Each edge that connects two overlapping objects has lower weight equal to the amount of overlapping between these objects in the x-direction plus one.
Each edge that connects an edge e of the original drawing to a label assigned to e has upper and lower weight zero.
Each remaining edge, other than edges connecting two vertical sides of labels, has lower weight one.
Each edge connecting the two vertical sides of a label has upper and lower weight equal to the width of the label.
Each edge, other than those connecting two vertical sides of a label or each edge e of the original drawing to a label assigned to e has upper weight equal to .
Next, we show that the minimum flow of produces the minimum width expansion needed to resolve overlaps.
Theorem 4. The minimum flow of gives the minimum width of the drawing, such that all overlaps are resolved in one direction, and the orthogonal representation of the drawing is preserved.
Proof. The resulting drawing has the same orthogonal representation since we do not allow flow to cross vertical edges of the drawing.
By construction, for any pair of overlapping labels, there will be enough flow going through to push them apart; thus, the resulting drawing has no overlaps.
Let us assume that the minimum flow of does not produce minimum width. This means that we have inserted extra vertical space. Therefore, there exists a path in from source to sink that carries at least one unit of extra flow. This is a contradiction, since we have obtained a minimum flow for . ☐
Sophisticated techniques can solve the minimum flow problem in
time [
19,
20], where
n is the number of vertices and
m is the number of edges of
. The coordinates of the resulting orthogonal drawing can be easily obtained, since the flow in each edge of
gives the offset of objects in the original drawing that the corresponding edge in the visibility graph connects.
6.3. Results and Discussion
Labeling of edges and nodes aims to communicate the attributes of these graph objects in the most convenient way. This requires that labels be positioned in the most appropriate places and follow some basic aesthetic quality rules [
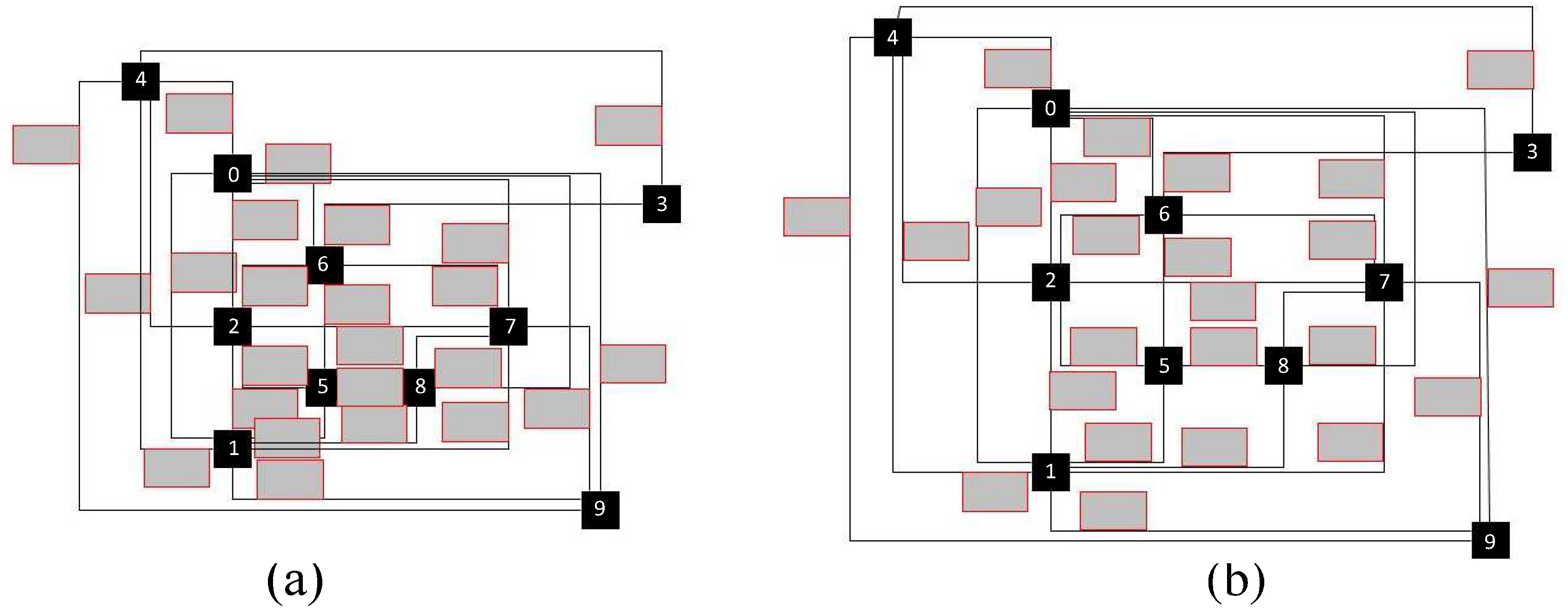
15]. In addition, for technical maps or drawings, additional sets of rules influence the preferred label positions. These rules depend on the particular application and follow user specifications. For example, a label of an edge that is relevant to its source node must be placed close to the source node to avoid ambiguity. Therefore, in order to resolve label overlaps (
Figure 21a), we must insert vertical space (
Figure 21c), even though we could relocate the label to eliminate overlaps without inserting extra space (
Figure 21b).
One point that we must emphasize is that the framework of the flow technique, in addition to resolving overlaps, can produce high quality label placement with respect to user’s preferences and aesthetic criteria. For example, in order to keep or place an edge label close to its associated node, we could assign a constant value to the upper and lower capacity of the edge in the flow graph that separates the node from each associated edge label.
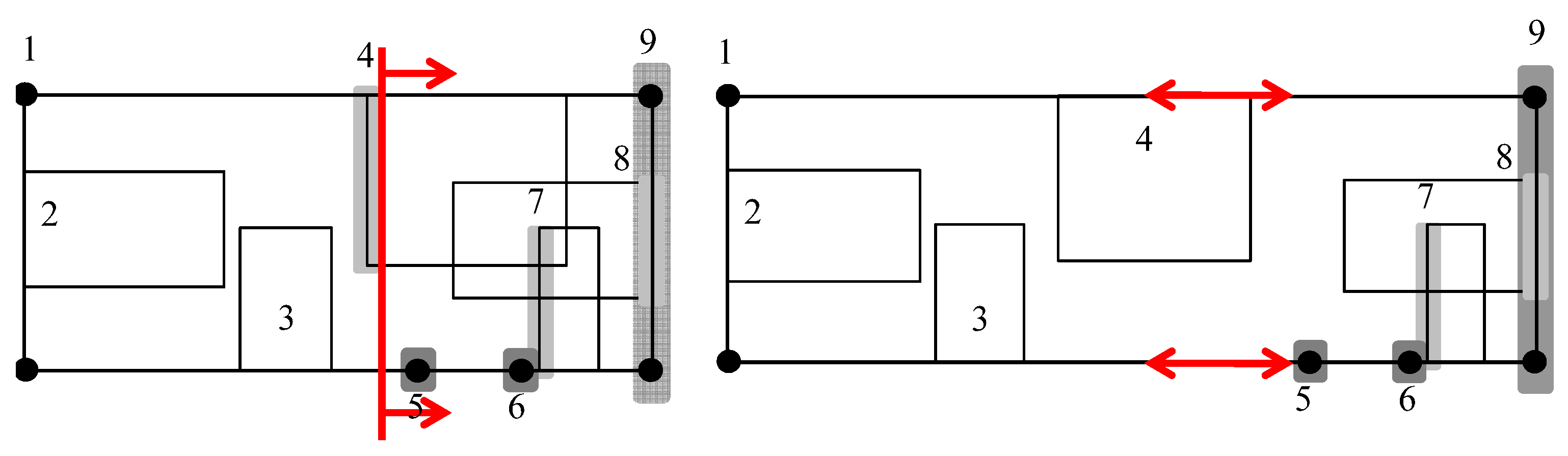
There are cases where overlaps of labels can be resolved by inserting extra space only in one direction. For example, in the orthogonal drawing shown in
Figure 22, label overlaps can be resolved only by inserting vertical space. For the orthogonal drawings shown in
Figure 2 and
Figure 23, overlaps can be resolved only by inserting horizontal and vertical extra space. Furthermore, for the orthogonal drawing shown in
Figure 24a, by running the algorithm once for each direction, we get better results. In
Figure 24b, we resolve all overlaps in the
x-direction; in
Figure 24c, we resolve all overlaps in the
y-direction; and in
Figure 24d, we resolve overlaps of two objects in the direction that they intersect less. For example, if two objects overlap more horizontally than vertically, then we resolve overlaps by increasing the height of the drawing.