Retrieval of Internal Solitary Wave Amplitude in Shallow Water by Tandem Spaceborne SAR
Abstract
:1. Introduction
2. Materials and Methods
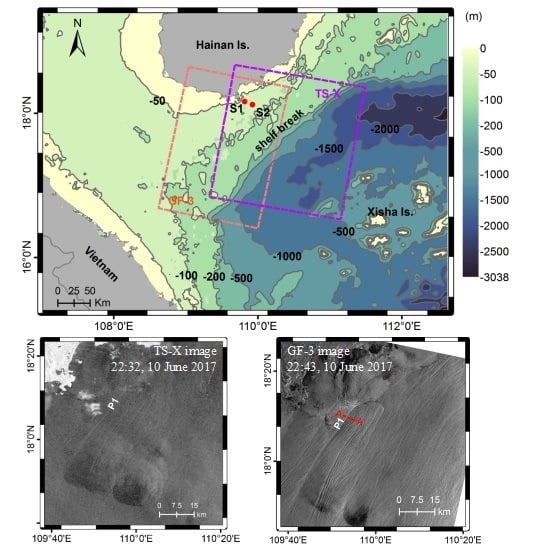
2.1. Brief Description of the Experiment
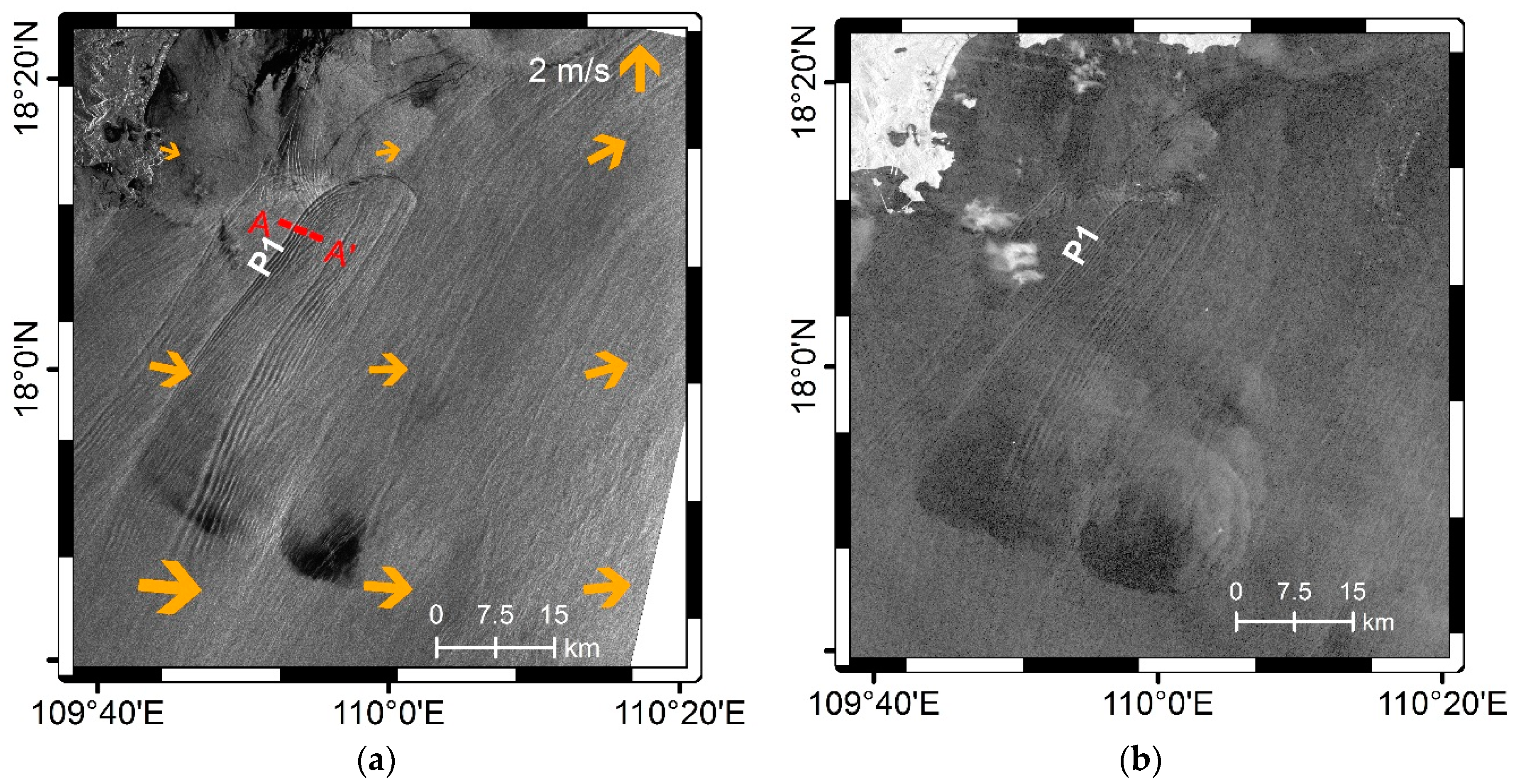
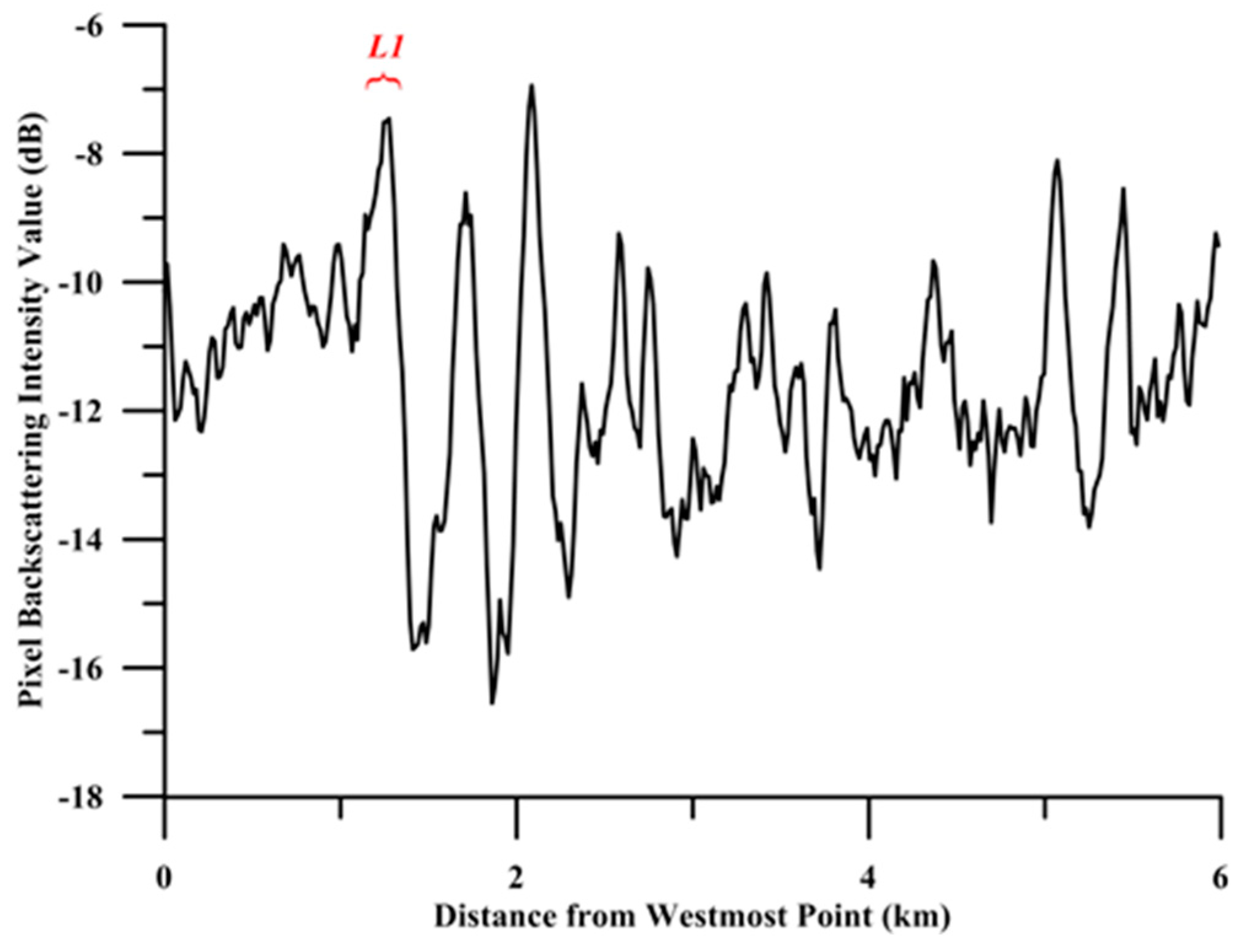
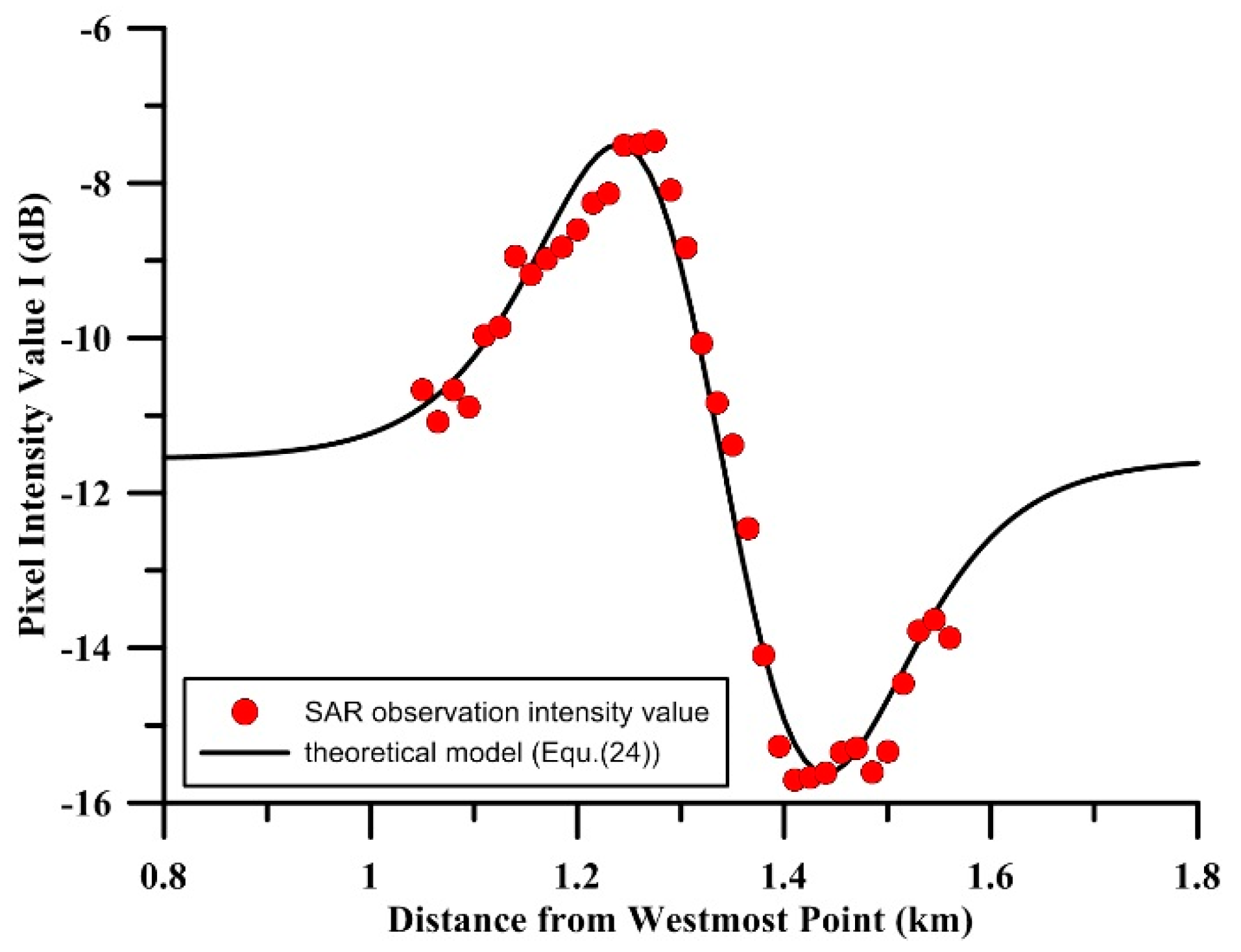
2.2. Processing of the Spaceborne SAR Data and Extraction of ISW Characteristics
2.3. CTD Data and WOA13 V2 Data
2.4. The Conventional Method of ISW Amplitude Estimation Based on the Classic KdV Equation in a Continuously Stratified Ocean Model
2.5. The Proposed Method of ISW Amplitude Estimation Based on the eKdV Equation in a Two-Layer Ocean Model
3. Results and Analysis
3.1. The Derived ISW Amplitude Using the Conventional Method
3.2. The Derived ISW Amplitude Using the Proposed Method
4. Discussion
5. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Magalhaes, J.M.; Da Silva, J.C.B. Internal solitary waves in the Andaman Sea: New insights from SAR imagery. Remote Sens. 2018, 10, 861. [Google Scholar] [CrossRef]
- Apel, J.R.; Holbrook, J.R.; Liu, A.K.; Tsai, J.J. The Sulu Sea internal soliton experiment. J. Phys. Oceanogr. 1985, 15, 1625–1651. [Google Scholar] [CrossRef]
- Liang, J.; Li, X.-M.; Sha, J.; Jia, T.; Ren, Y. The lifecycle of nonlinear internal waves in the northwestern South China Sea. J. Phys. Oceanogr. 2019. [Google Scholar] [CrossRef]
- Lavrova, O.; Mityagina, M. Satellite survey of internal waves in the Black and Caspian Seas. Remote Sens. 2017, 9, 892. [Google Scholar] [CrossRef]
- Sandstrom, H.; Elliott, J.A. Internal tide and solitons on the Scotian Shelf: A nutrient pump at work. J. Geophys. Res. Oceans 1984, 89, 6415–6426. [Google Scholar] [CrossRef]
- Nash, J.D.; Shroyer, E.L.; Kelly, S.M.; Inall, M.E.; Duda, T.F.; Levine, M.D.; Jones, N.L.; Musgrave, R.C. Are any coastal internal tides predictable? Oceanography 2012, 25, 80–95. [Google Scholar] [CrossRef]
- Osborne, A.R.; Burch, T.L.; Scarlet, R.I. The influence of internal waves on deep-water drilling. J. Pet. Technol. 1978, 30, 1497–1504. [Google Scholar] [CrossRef]
- Horne, E.; Beckebanze, F.; Micard, D.; Odier, P.; Maas, L.R.M.; Joubaud, S. Particle transport induced by internal wave beam streaming in lateral boundary layers. J. Fluid Mech. 2019, 870, 848–869. [Google Scholar] [CrossRef] [Green Version]
- Chiu, C.S.; Ramp, S.R.; Miller, C.W.; Lynch, J.F.; Duda, T.F.; Tang, T.Y. Acoustic intensity fluctuations induced by South China Sea internal tides and solitons. IEEE J. Ocean. Eng. 2004, 29, 1249–1263. [Google Scholar] [CrossRef]
- Woodson, C.B. The fate and impact of internal waves in nearshore ecosystems. Annu. Rev. Mar. Sci. 2018, 10, 421–441. [Google Scholar] [CrossRef]
- Jackson, C.R.; Da Silva, J.C.B.; Jeans, G.; Alpers, W.; Caruso, M.J. Nonlinear internal waves in synthetic aperture radar imagery. Oceanography 2013, 26, 68–79. [Google Scholar] [CrossRef]
- Alpers, W. Theory of radar imaging of internal waves. Nature 1985, 314, 245–247. [Google Scholar] [CrossRef]
- Porter, D.L.; Thompson, D.R. Continental shelf parameters inferred from SAR internal wave observations. J. Atmos. Ocean. Technol. 1999, 16, 475–487. [Google Scholar] [CrossRef]
- Fan, K.; Fu, B.; Gu, Y.; Yu, X.; Liu, T.; Shi, A.; Xu, K.; Gan, X. Internal wave parameters retrieval from space-borne SAR image. Front. Earth Sci. 2015, 9, 700–708. [Google Scholar] [CrossRef]
- Wang, J.; Yang, J.; Li, J.; Ren, L.; Zheng, G. Study on extracting and verifying internal wave parameter of SAR image. In Proceedings of the SPIE 9638, Remote Sensing of the Ocean, Sea Ice, Coastal Waters, and Large Water Regions 2015, Toulouse, France, 23 September 2015. [Google Scholar] [CrossRef]
- Romeiser, R.; Graber, H.C. Advanced remote sensing of internal waves by spaceborne along-track InSAR-A demonstration with TerraSAR-X. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6735–6751. [Google Scholar] [CrossRef]
- Wang, C.; Wang, X.; Da Silva, J.C.B. Studies of internal waves in the strait of Georgia based on remote sensing images. Remote Sens. 2019, 11, 96. [Google Scholar] [CrossRef]
- Small, J.; Hallock, Z.; Pavey, G.; Scott, J. Observations of large amplitude internal waves at the Malin Shelf edge during SESAME 1995. Cont. Shelf Res. 1999, 19, 1389–1436. [Google Scholar] [CrossRef]
- Pan, J.; Jay, D.A.; Orton, P.M. Analyses of internal solitary waves generated at the Columbia River plume front using SAR imagery. J. Geophys. Res. Oceans 2007, 112. [Google Scholar] [CrossRef] [Green Version]
- Zheng, Q.; Yuan, Y.; Klemas, V.; Yan, X. Theoretical expression for an ocean internal soliton synthetic aperture radar image and determination of the soliton characteristic half width. J. Geophys. Res. Oceans 2001, 106, 31415–31423. [Google Scholar] [CrossRef]
- Xue, J.; Graber, H.C.; Lund, B.; Romeiser, R. Amplitudes estimation of large internal solitary waves in the Mid-Atlantic Bight using synthetic aperture radar and marine X-band radar images. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3250–3258. [Google Scholar] [CrossRef]
- Hong, D.-B.; Yang, C.-S.; Ouchi, K. Preliminary study of internal solitary wave amplitude off the East coast of Korea based on synthetic aperture radar data. J. Mar. Sci. Technol. Taiwan 2016, 24, 1194–1203. [Google Scholar] [CrossRef]
- Benjamin, T.B. Internal waves of finite amplitude and permanent form. J. Fluid Mech. 1966, 25, 241–270. [Google Scholar] [CrossRef] [Green Version]
- Benney, D.J. Long non-linear waves in fluid flows. J. Math Phys. 1966, 45, 52–63. [Google Scholar] [CrossRef]
- Joseph, R.I. Solitary waves in a finite depth fluid. J. Phys. A Math. Gen. 1977, 10, L225–L227. [Google Scholar] [CrossRef]
- Kubota, T.; Ko, D.R.S.; Dobbs, L. Propagation of weakly nonlinear internal waves in a stratified fluid of finite depth. J. Hydronaut. 1978, 12, 157–165. [Google Scholar] [CrossRef]
- Benjamin, T.B. Internal waves of permanent form in fluids of great depth. J. Fluid Mech. 1967, 29, 559–592. [Google Scholar] [CrossRef]
- Ono, H. Algebraic solitary waves in stratified fluids. J. Phys. Soc. Jpn. 1975, 39, 1082–1091. [Google Scholar] [CrossRef]
- Rodenas, J.A.; Garello, R. Wavelet analysis in SAR ocean image profiles for internal wave detection and wavelength estimation. IEEE Trans. Geosci. Remote Sens. 1997, 35, 933–945. [Google Scholar] [CrossRef]
- Gan, X. A new method to extract internal wave parameters from SAR imagery with Hilbert-Huang transform. J. Remote Sens. 2007, 11, 39–47. [Google Scholar]
- Wang, P.; Wang, X.; Chong, J.; Lu, Y. Optimal parameter estimation method of internal solitary waves in SAR images and the Cramér–Rao bound. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3143–3150. [Google Scholar] [CrossRef]
- Chen, G.-Y.; Wu, C.-L.; Wang, Y.-H. Interface depth used in a two-layer model of nonlinear internal waves. J. Oceanogr. 2014, 70, 329–342. [Google Scholar] [CrossRef]
- Zhao, Z.; Klemas, V.; Zheng, Q.; Li, X.; Yan, X.-H. Estimating parameters of a two-layer stratified ocean from polarity conversion of internal solitary waves observed in satellite SAR images. Remote Sens. Environ. 2004, 92, 276–287. [Google Scholar] [CrossRef]
- Li, X.; Clemente-Colón, P.; Friedman, K.S. Estimating oceanic mixed-layer depth from internal wave evolution observed from Radarsat-1 SAR. Johns Hopkins APL Tech. Dig. 2000, 21, 130–135. [Google Scholar]
- Yang, J.; Huang, W.; Xiao, Q.; Zhou, C.; Hsu, M.K. Oceanic pycnocline depth retrieval from SAR imagery in the existence of solitary internal waves. Acta Oceanol. Sin. 2005, 24, 46–49. [Google Scholar]
- Liu, B.; Yang, H.; Zhao, Z.; Li, X. Internal solitary wave propagation observed by tandem satellites. J. Geophys. Res. Oceans 2014, 41, 2077–2085. [Google Scholar] [CrossRef]
- Plant, W.J. Bragg scattering of electromagnetic waves from the air/sea interface. In Surface Waves and Fluxes; Geernaert, G.L., Plant, W.J., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherland, 1990; Volume II, pp. 41–108. [Google Scholar]
- Helfrich, K.R.; Melville, W.K. Long nonlinear internal waves. Annu. Rev. Fluid Mech. 2006, 38, 395–425. [Google Scholar] [CrossRef]
- Grimshaw, R. Internal solitary waves. In Environmental Stratified Flows; Grimshaw, R., Ed.; Kluwer Academic Publishers: Boston, MA, USA, 2003; pp. 1–27. [Google Scholar]
- Grimshaw, R.; Pelinovsky, E.; Talipova, T.; Kurkin, A. Simulation of the transformation of internal solitary waves on oceanic shelves. J. Phys. Oceanogr. 2004, 34, 2774–2791. [Google Scholar] [CrossRef]
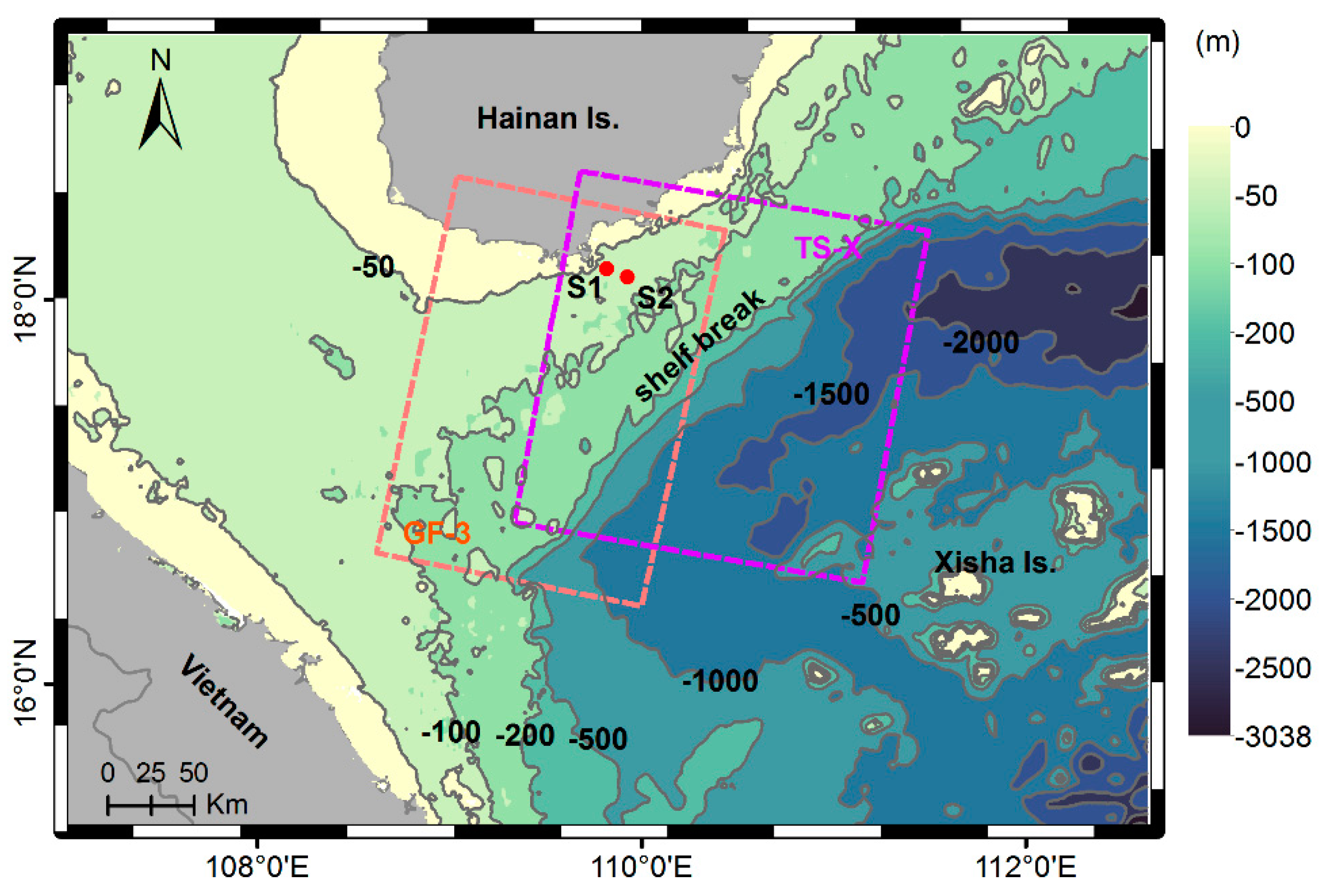




| SAR | Acquisition Time (UTC) and Date | Imaging Mode | Resolution (m) | Incidence Angle (°) | Polarization |
|---|---|---|---|---|---|
| TS-X | 22:32 10 June 2017 | ScanSAR | 36 | 34.59–48.75 | VV1 |
| GF-3 | 22:43 10 June 2017 | Standard stripmap | 8 | 15.23–26.57 | VV-VH1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, T.; Liang, J.; Li, X.-M.; Fan, K. Retrieval of Internal Solitary Wave Amplitude in Shallow Water by Tandem Spaceborne SAR. Remote Sens. 2019, 11, 1706. https://0-doi-org.brum.beds.ac.uk/10.3390/rs11141706
Jia T, Liang J, Li X-M, Fan K. Retrieval of Internal Solitary Wave Amplitude in Shallow Water by Tandem Spaceborne SAR. Remote Sensing. 2019; 11(14):1706. https://0-doi-org.brum.beds.ac.uk/10.3390/rs11141706
Chicago/Turabian StyleJia, Tong, Jianjun Liang, Xiao-Ming Li, and Kaiguo Fan. 2019. "Retrieval of Internal Solitary Wave Amplitude in Shallow Water by Tandem Spaceborne SAR" Remote Sensing 11, no. 14: 1706. https://0-doi-org.brum.beds.ac.uk/10.3390/rs11141706