Compression of Hyperspectral Scenes through Integer-to-Integer Spectral Graph Transforms †
Abstract
:1. Introduction
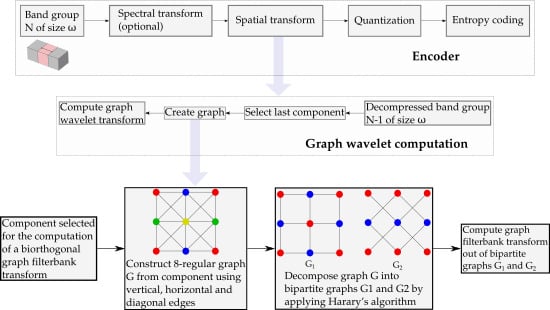
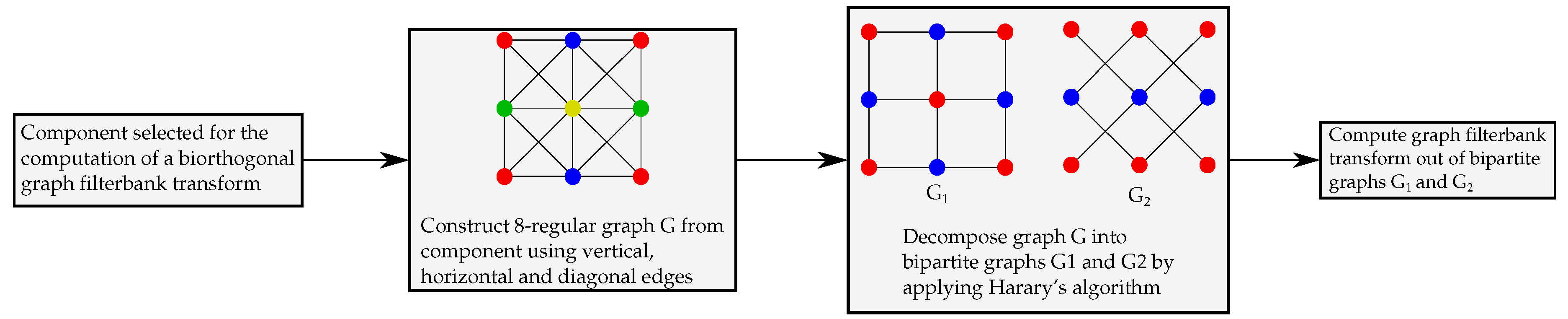
2. Graphs and Biorthogonal Graph Wavelets
3. Lossy-to-Lossless Graph Wavelet Filterbanks
3.1. Compression Scheme
3.2. TERM factorization of GraphBior
3.3. Tiling
3.4. Integer-to-Integer Spectral Graph Lifting
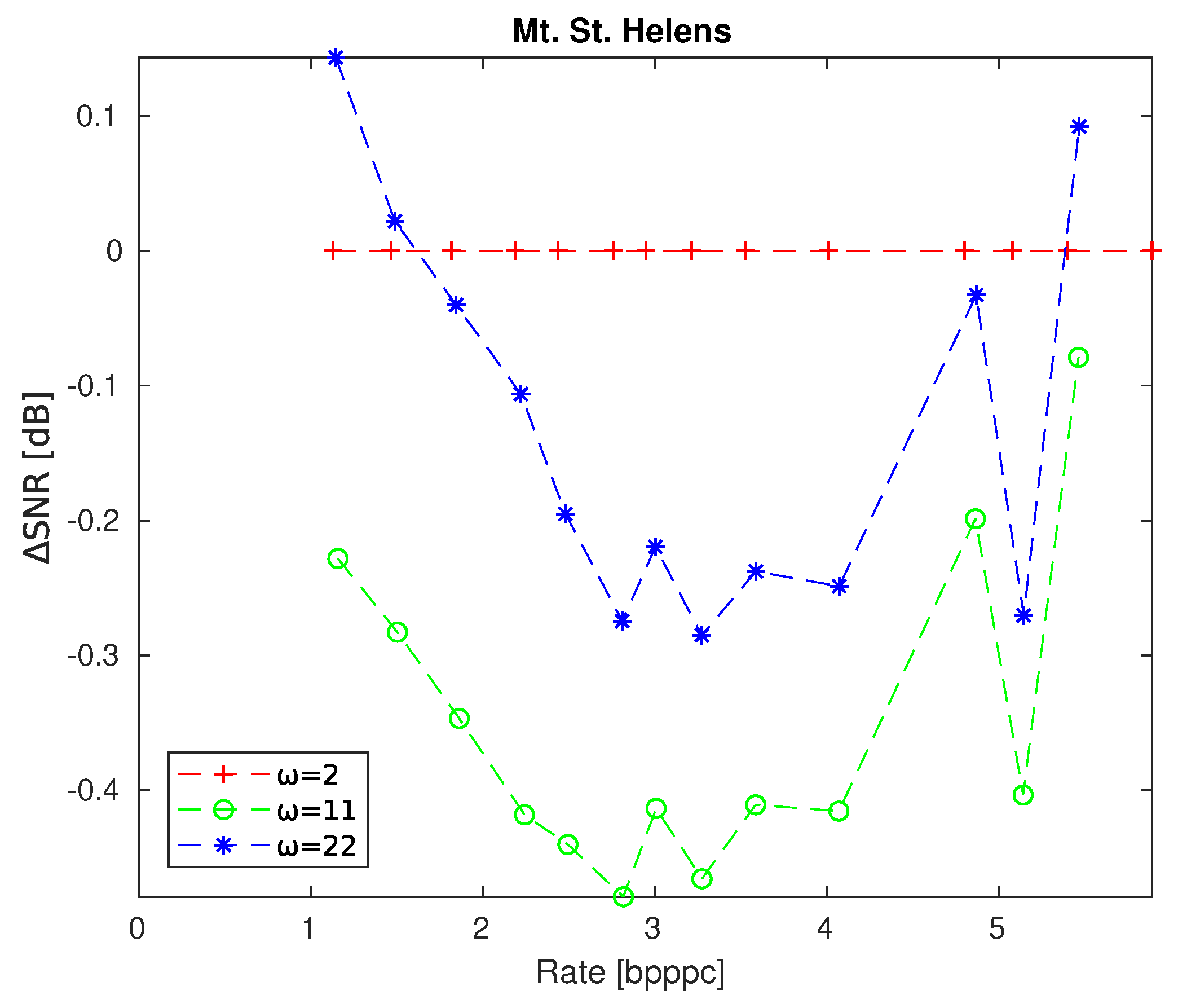
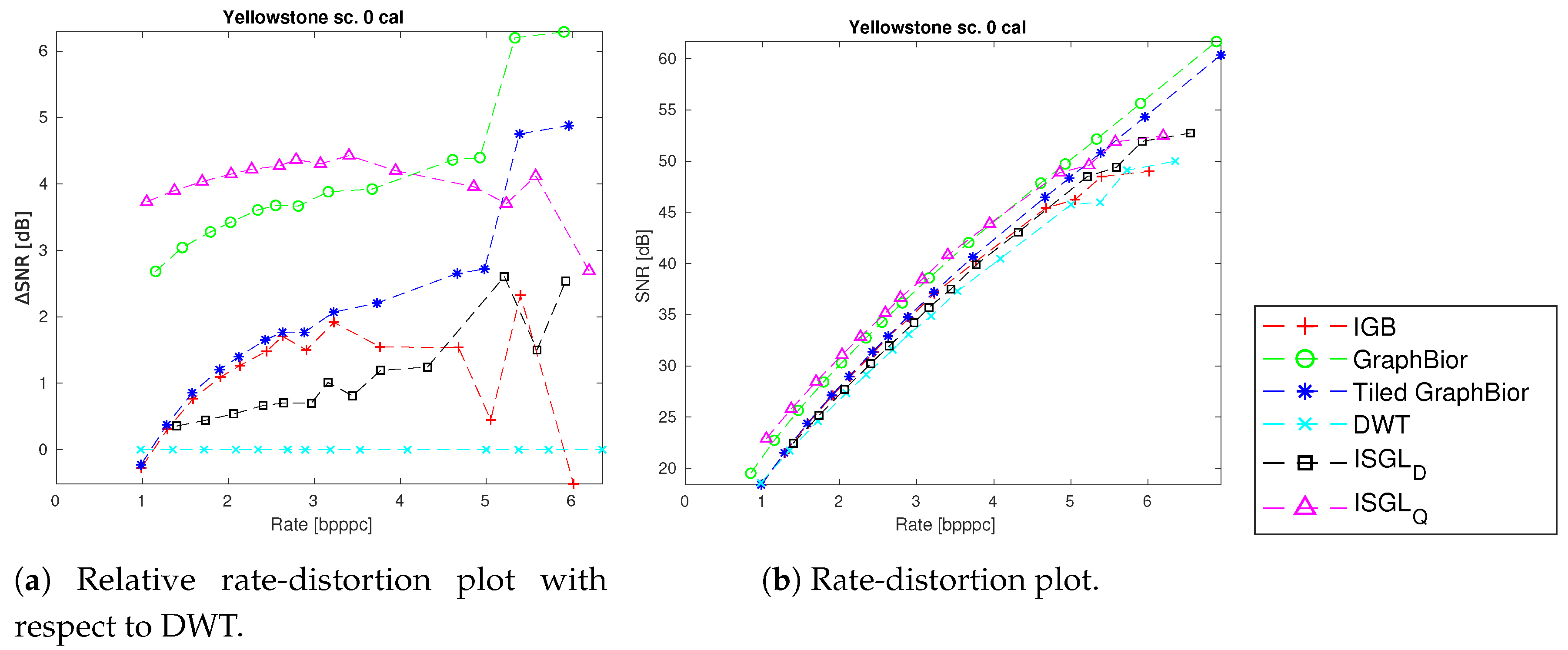
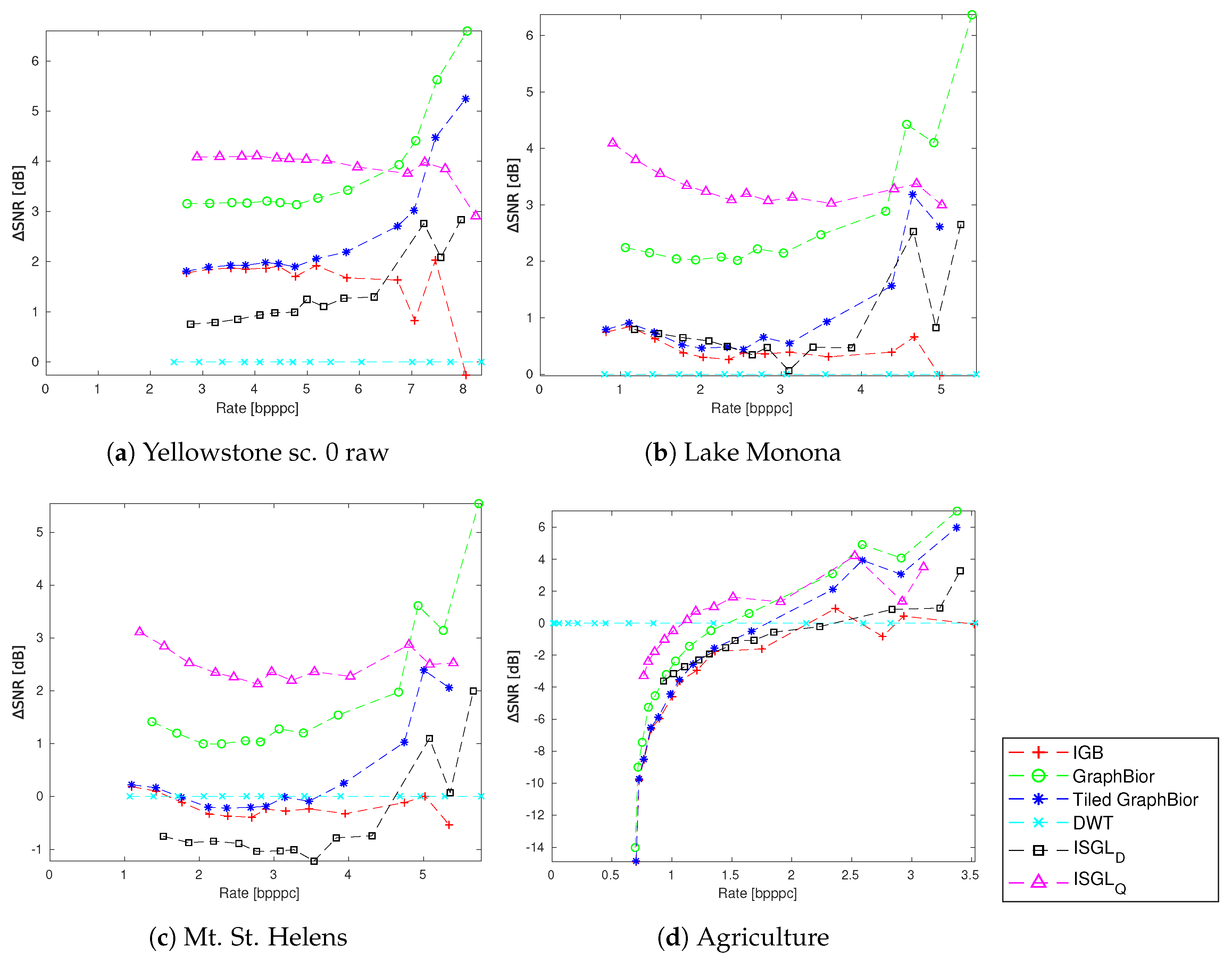
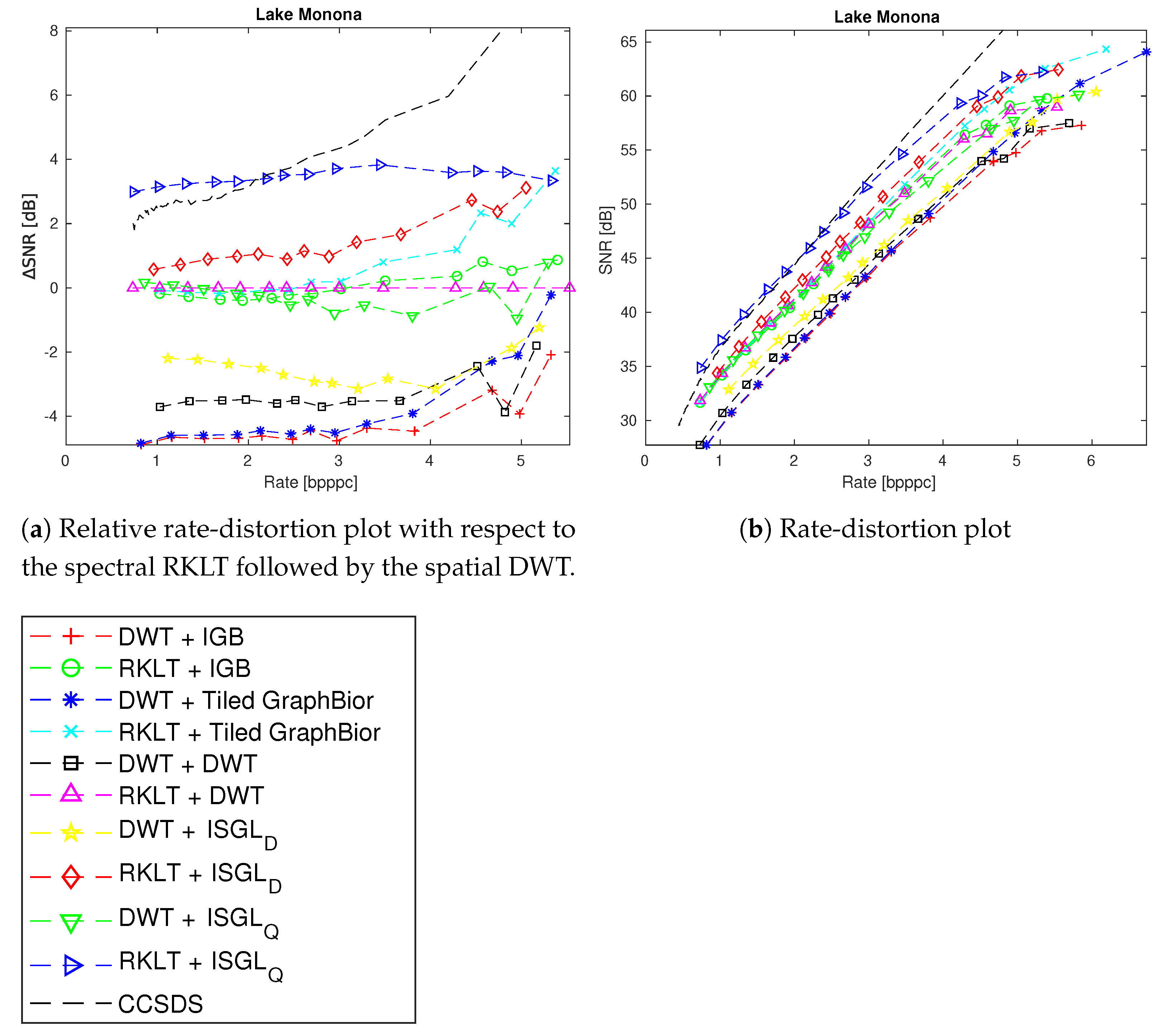
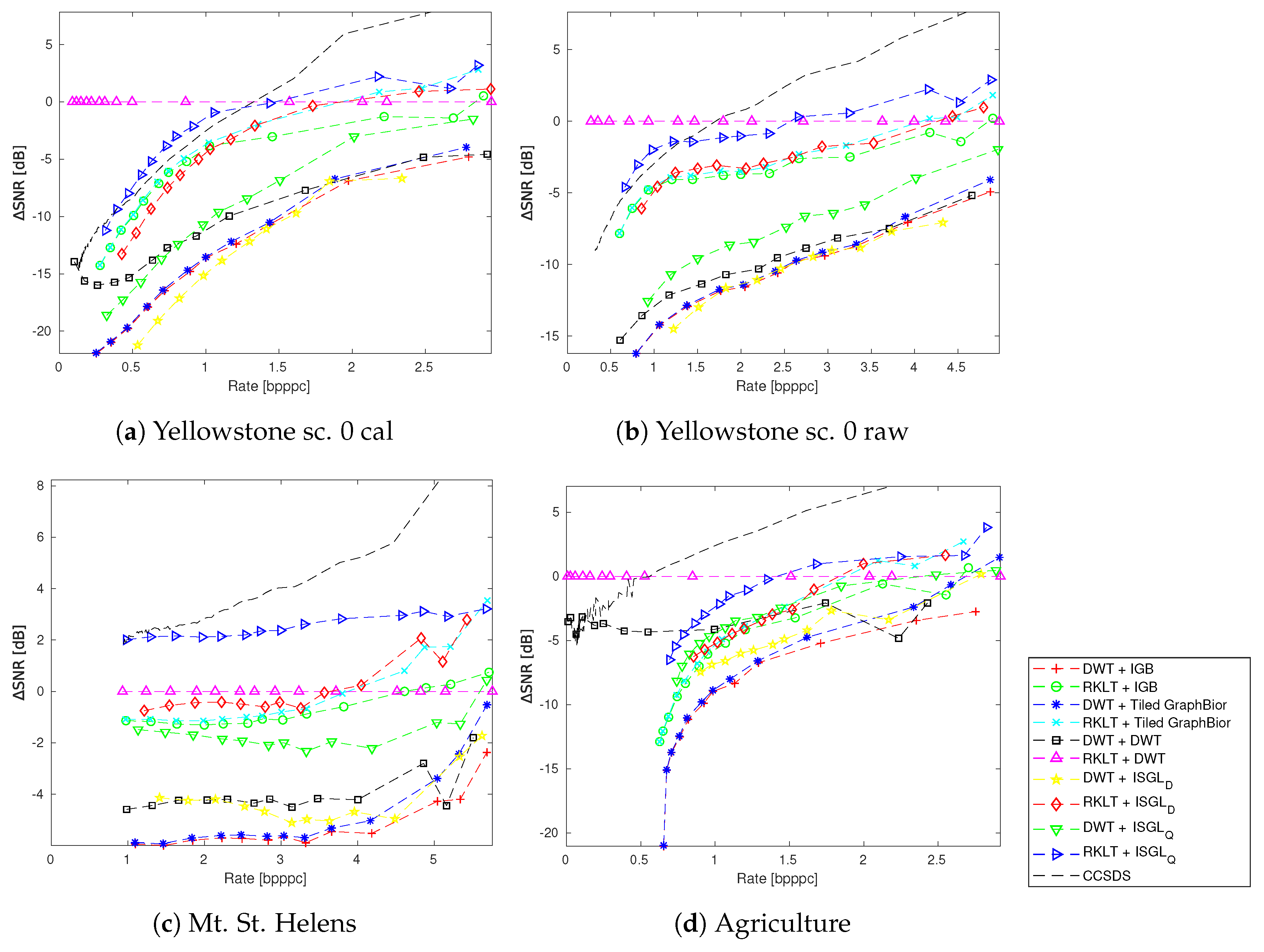
4. Experimental Results
4.1. Parameter Variations
4.2. Spatial Transformations
4.3. Spectral and Spatial Transformations
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liang, H.; Li, Q. Hyperspectral imagery classification using sparse representations of convolutional neural network features. Remote Sens. 2016, 8, 99. [Google Scholar] [CrossRef]
- Thompson, D.R.; Green, R.O.; Keymeulen, D.; Lundeen, S.K.; Mouradi, Y.; Nunes, D.C.; Castaño, R.; Chien, S.A. Rapid spectral cloud screening onboard aircraft and spacecraft. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6779–6792. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, F.; He, Y.; Li, X. Application of hyperspectral imaging and chemometric calibrations for variety discrimination of maize seeds. Sensors 2012, 12, 17234–17246. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Niu, R. Spatial forecast of landslides in three gorges based on spatial data mining. Sensors 2009, 9, 2035–2061. [Google Scholar] [CrossRef]
- Tang, X.; Pearlman, W.A. Three-dimensional wavelet-based compression of hyperspectral images. In Hyperspectral Data Compression; Springer: Boston, MA, USA, 2006; pp. 273–308. [Google Scholar]
- Fowler, J.E.; Rucker, J.T. Three-dimensional wavelet-based compression of hyperspectral imagery. In Hyperspectral Data Exploitation: Theory and Applications; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007; pp. 379–407. [Google Scholar]
- Karami, A.; Yazdi, M.; Mercier, G. Compression of hyperspectral images using discerete wavelet transform and tucker decomposition. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 444–450. [Google Scholar] [CrossRef]
- Tang, X.; Pearlman, W.A.; Modestino, J.W. Hyperspectral image compression using three-dimensional wavelet coding. In Image and Video Communications and Processing 2003; International Society for Optics and Photonics: Bellingham, WA, USA, 2003; Volume 5022, pp. 1037–1047. [Google Scholar]
- Du, Q.; Fowler, J.E. Hyperspectral image compression using JPEG2000 and principal component analysis. IEEE Geosci. Remote Sens. Lett. 2007, 4, 201–205. [Google Scholar] [CrossRef]
- Penna, B.; Tillo, T.; Magli, E.; Olmo, G. Transform coding techniques for lossy hyperspectral data compression. IEEE Geosci. Remote Sens. Lett. 2007, 45, 1408–1421. [Google Scholar] [CrossRef]
- Penna, B.; Tillo, T.; Magli, E.; Olmo, G. A new low complexity KLT for lossy hyperspectral data compression. In Proceedings of the 2006 IEEE International Symposium on Geoscience and Remote Sensing, Denver, CO, USA, 31 July–4 August 2006; pp. 3525–3528. [Google Scholar]
- Galli, L.; Salzo, S. Lossless hyperspectral compression using KLT. In Proceedings of the 2004 IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2004), Anchorage, AK, USA, 20–24 September 2004; Volume 1. [Google Scholar]
- Rizzo, F.; Carpentieri, B.; Motta, G.; Storer, J.A. Low-complexity lossless compression of hyperspectral imagery via linear prediction. IEEE Signal Process. Lett. 2005, 12, 138–141. [Google Scholar] [CrossRef]
- Pizzolante, R.; Carpentieri, B. Multiband and lossless compression of hyperspectral images. Algorithms 2016, 9, 16. [Google Scholar] [CrossRef]
- Abrardo, A.; Barni, M.; Magli, E. Low-complexity predictive lossy compression of hyperspectral and ultraspectral images. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 797–800. [Google Scholar]
- Klimesh, M. Low-complexity adaptive lossless compression of hyperspectral imagery. In Proceedings of the Satellite Data Compression, Communications, and Archiving II, San Diego, CA, USA, 13–17 August 2006; Volume 6300, p. 63000N. [Google Scholar]
- Klimesh, M.; Kiely, A.; Yeh, P. Fast lossless compression of multispectral and hyperspectral imagery. In Proceedings of the 2nd International Workshop on On-Board Payload Data Compression (OBPDC), Toulouse, France, 28–29 October 2010; Volume 8, pp. 28–29. [Google Scholar]
- Consultative Committee for Space Data Systems. Lossless and Near-Lossless Multispectral and Hyperspectral Image Compression. Recommendation for Space Data System Standards, CCSDS 123.0-B-2; CCSDS: Washington, DC, USA, 2019. [Google Scholar]
- Blanes, I.; Kiely, A.; Hernández-Cabronero, M.; Serra-Sagristà, J. Performance Impact of Parameter Tuning on the CCSDS-123.0-B-2 Low-Complexity Lossless and Near-Lossless Multispectral and Hyperspectral Image Compression Standard. Remote Sens. 2019, 11, 1390. [Google Scholar] [CrossRef]
- Shuman, D.I.; Narang, S.K.; Frossard, P.; Ortega, A.; Vandergheynst, P. The emerging field of signal processing on graphs: Extending high-dimensional data analysis to networks and other irregular domains. IEEE Signal Process. Mag. 2013, 30, 83–98. [Google Scholar] [CrossRef] [Green Version]
- Ortega, A.; Frossard, P.; Kovačević, J.; Moura, J.M.; Vandergheynst, P. Graph signal processing: Overview, challenges, and applications. Proc. IEEE 2018, 106, 808–828. [Google Scholar] [CrossRef]
- Zeng, J.; Cheung, G.; Chao, Y.H.; Blanes, I.; Serra-Sagristà, J.; Ortega, A. Hyperspectral image coding using graph wavelets. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017. [Google Scholar]
- Cheung, G.; Magli, E.; Tanaka, Y.; Ng, M.K. Graph spectral image processing. Proc. IEEE 2018, 106, 907–930. [Google Scholar] [CrossRef]
- Hu, W.; Cheung, G.; Ortega, A.; Au, O.C. Multiresolution graph fourier transform for compression of piecewise smooth images. IEEE Trans. Image Process. 2014, 24, 419–433. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Florêncio, D. Analyzing the optimality of predictive transform coding using graph-based models. IEEE Signal Process. Lett. 2012, 20, 106–109. [Google Scholar] [CrossRef]
- Narang, S.K.; Ortega, A. Lifting based wavelet transforms on graphs. In Proceedings of the APSIPA ASC 2009: Asia-Pacific Signal and Information Processing Association, 2009 Annual Summit and Conference, Sapporo, Japan, 4–7 October 2009; pp. 441–444. [Google Scholar]
- Coifman, R.R.; Maggioni, M. Diffusion wavelets. Appl. Comput. Harmonic Anal. 2006, 21, 53–94. [Google Scholar] [CrossRef] [Green Version]
- Hammond, D.K.; Vandergheynst, P.; Gribonval, R. Wavelets on graphs via spectral graph theory. Appl. Comput. Harmonic Anal. 2011, 30, 129–150. [Google Scholar] [CrossRef] [Green Version]
- Narang, S.K.; Ortega, A. Perfect reconstruction two-channel wavelet filter banks for graph structured data. IEEE Trans. Signal Process. 2012, 60, 2786–2799. [Google Scholar] [CrossRef]
- Narang, S.K.; Ortega, A. Compact support biorthogonal wavelet filterbanks for arbitrary undirected graphs. IEEE Trans. Signal Process. 2013, 61, 4673–4685. [Google Scholar] [CrossRef]
- Sakiyama, A.; Watanabe, K.; Tanaka, Y.; Ortega, A. Two-Channel Critically Sampled Graph Filter Banks with Spectral Domain Sampling. IEEE Trans. Signal Process. 2019, 67, 1447–1460. [Google Scholar] [CrossRef]
- Li, S.; Jin, Y.; Shuman, D.I. Scalable M-Channel Critically Sampled Filter Banks for Graph Signals. IEEE Trans. Signal Process. 2019, 67, 3954–3969. [Google Scholar] [CrossRef]
- Tay, D.B.; Ortega, A. Bipartite graph filter banks: Polyphase analysis and generalization. IEEE Trans. Signal Process. 2017, 65, 4833–4846. [Google Scholar] [CrossRef]
- Tay, D.B.; Ortega, A.; Anis, A. Cascade and Lifting Structures in the Spectral Domain for Bipartite Graph Filter Banks. In Proceedings of the 2018 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Honolulu, HI, USA, 12–15 November 2018; pp. 1141–1147. [Google Scholar]
- Hao, P.; Shi, Q. Matrix factorizations for reversible integer mapping. IEEE Trans. Signal Process. 2001, 49, 2314–2324. [Google Scholar] [Green Version]
- Consultative Committee for Space Data Systems, Test Data. Available online: http://cwe.ccsds.org/sls/docs/sls-dc/123.0-B-Info/TestData (accessed on 3 March 2019).
- Harary, F.; Hsu, D.; Miller, Z. The biparticity of a graph. J. Graph Theory 1977, 1, 131–133. [Google Scholar] [CrossRef]
- Narang, S.K.; Ortega, A. Multi-dimensional separable critically sampled wavelet filterbanks on arbitrary graphs. In Proceedings of the 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012; pp. 3501–3504. [Google Scholar]
- Nguyen, H.Q.; Do, M.N. Downsampling of signals on graphs via maximum spanning trees. IEEE Trans. Signal Process. 2014, 63, 182–191. [Google Scholar] [CrossRef]
- Zeng, J.; Cheung, G.; Ortega, A. Bipartite approximation for graph wavelet signal decomposition. IEEE Trans. Signal Process. 2017, 65, 5466–5480. [Google Scholar] [CrossRef]
- Tay, D.B.; Zhang, J. Techniques for constructing biorthogonal bipartite graph filter banks. IEEE Trans. Signal Process. 2015, 63, 5772–5783. [Google Scholar] [CrossRef]
- Hao, P.; Shi, Q. Reversible integer KLT for progressive-to-lossless compression of multiple component images. In Proceedings of the 2003 International Conference on Image Processing (Cat. No. 03CH37429), Barcelona, Spain, 14–17 September 2003; Volume 1, pp. 1–633. [Google Scholar]





| Name | Instrument | Calibrated | Across-Track | Along-Track | Spectral Dimension |
|---|---|---|---|---|---|
| Yellowstone sc. 0 cal. | AVIRIS | Yes | 512 | 512 | 224 |
| Yellowstone sc. 0 raw | AVIRIS | No | 512 | 512 | 224 |
| Lake Monona | Hyperion | Yes | 512 | 256 | 242 |
| Mt. St. Helens | Hyperion | Yes | 512 | 256 | 242 |
| Agriculture | Landsat | No | 512 | 512 | 6 |
| Image | IGB | ||
|---|---|---|---|
| Tiles of 8 by 8 | Tiles of 16 by 16 | Tiles of 32 by 32 | |
| Yellowstone sc. 0 cal. | 7.14 | 6.95 | - |
| Yellowstone sc. 0 raw | 9.15 | 9.02 | - |
| Lake Monona | 6.40 | 6.31 | 6.26 |
| Mt. St. Helens | 6.78 | 6.68 | 6.63 |
| Agriculture | 4.39 | 4.27 | 4.21 |
| Image | IGB | ||||||
|---|---|---|---|---|---|---|---|
| Yellowstone sc. 0 cal. | 6.95 | 7.00 | 7.06 | 7.14 | |||
| Yellowstone sc. 0 raw | 9.02 | 9.06 | 9.14 | 9.15 | |||
| Lake Monona | 6.31 | 6.36 | 6.37 | ||||
| Mt. St. Helens | 6.68 | 6.75 | 6.75 | ||||
| Agriculture | 4.27 | 4.39 | |||||
| Image | Transform | |||
|---|---|---|---|---|
| IGB | DWT | ISGLD | ISGLQ | |
| Yellowstone sc. 0 cal. | 6.95 | 7.29 | 7.44 | 7.11 |
| Yellowstone sc. 0 raw | 9.02 | 9.32 | 9.47 | 9.19 |
| Lake Monona | 6.26 | 6.23 | 6.50 | 6.28 |
| Mt. St. Helens | 6.63 | 6.57 | 6.93 | 6.67 |
| Agriculture | 4.21 | 4.37 | 4.67 | 4.37 |
| Image | Transforms | CCSDS | |||||||
|---|---|---|---|---|---|---|---|---|---|
| DWT + IGB | RKLT + IGB | DWT + DWT | DWT + ISGLD | DWT + ISGLQ | RKLT + DWT | RKLT + ISGLD | RKLT + ISGLQ | ||
| Yellowstone sc. 0 cal. | 5.03 | 4.41 | 4.73 | 5.36 | 5.05 | 3.74 | 4.65 | 4.36 | 4.04 |
| Yellowstone sc. 0 raw | 7.17 | 6.47 | 6.97 | 7.54 | 7.25 | 5.93 | 6.72 | 6.44 | 6.19 |
| Lake Monona | 6.69 | 6.19 | 6.56 | 6.89 | 6.66 | 6.35 | 6.34 | 6.13 | 6.10 |
| Mt. St. Helens | 7.06 | 6.52 | 6.90 | 7.32 | 7.05 | 6.58 | 6.71 | 6.47 | 6.37 |
| Agriculture | 4.21 | 3.96 | 3.96 | 4.63 | 4.34 | 3.68 | 4.37 | 4.08 | 3.62 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tzamarias, D.E.O.; Chow, K.; Blanes, I.; Serra-Sagristà, J. Compression of Hyperspectral Scenes through Integer-to-Integer Spectral Graph Transforms. Remote Sens. 2019, 11, 2290. https://0-doi-org.brum.beds.ac.uk/10.3390/rs11192290
Tzamarias DEO, Chow K, Blanes I, Serra-Sagristà J. Compression of Hyperspectral Scenes through Integer-to-Integer Spectral Graph Transforms. Remote Sensing. 2019; 11(19):2290. https://0-doi-org.brum.beds.ac.uk/10.3390/rs11192290
Chicago/Turabian StyleTzamarias, Dion Eustathios Olivier, Kevin Chow, Ian Blanes, and Joan Serra-Sagristà. 2019. "Compression of Hyperspectral Scenes through Integer-to-Integer Spectral Graph Transforms" Remote Sensing 11, no. 19: 2290. https://0-doi-org.brum.beds.ac.uk/10.3390/rs11192290