Comparison of TanDEM-X DEM with LiDAR Data for Accuracy Assessment in a Coastal Urban Area
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Study Area
2.2. Data
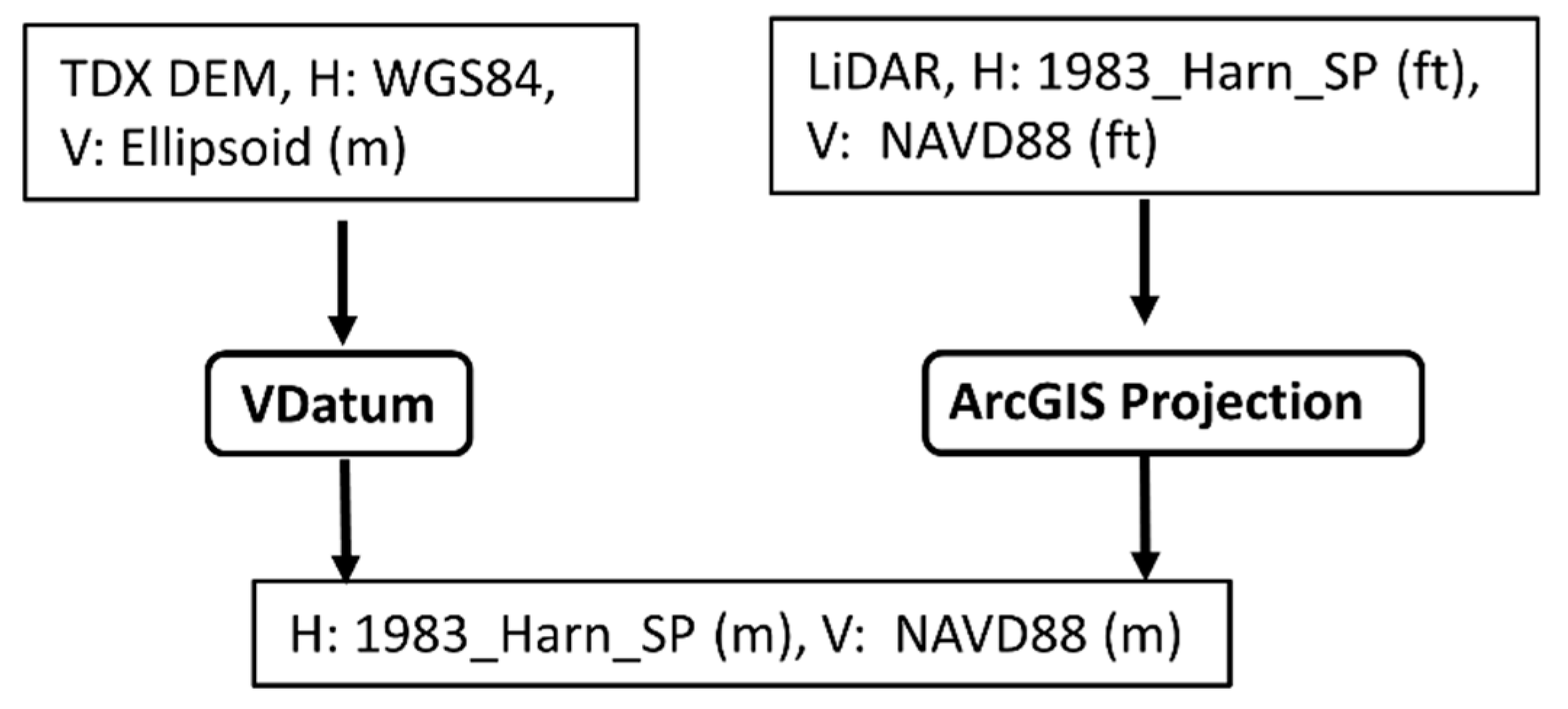
2.3. Datum Conversion
2.4. Accuracy Analysis
3. Results
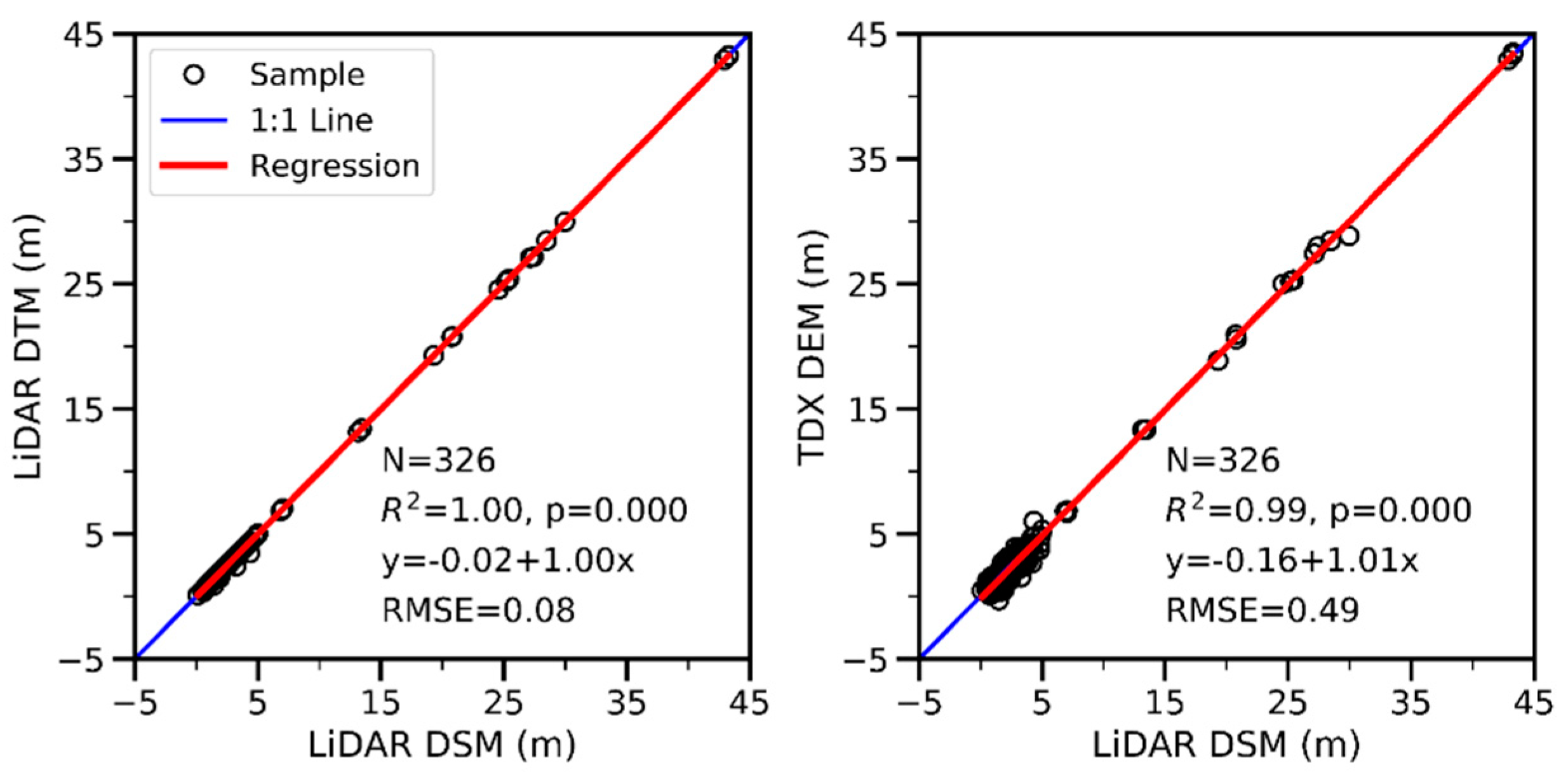
3.1. LiDAR DTM Accuracy and Horizontal Accuracy of TDX DEM
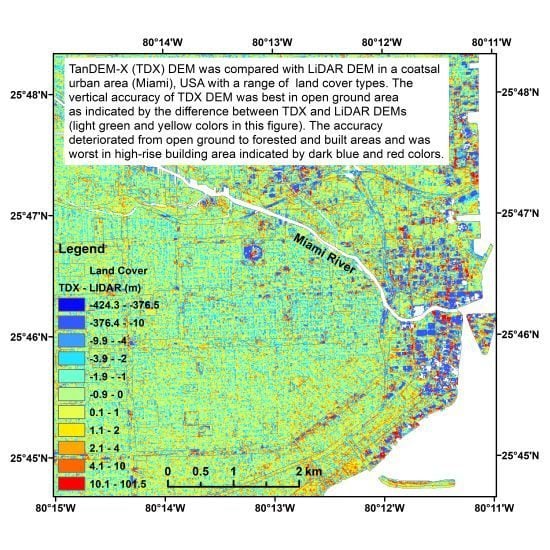
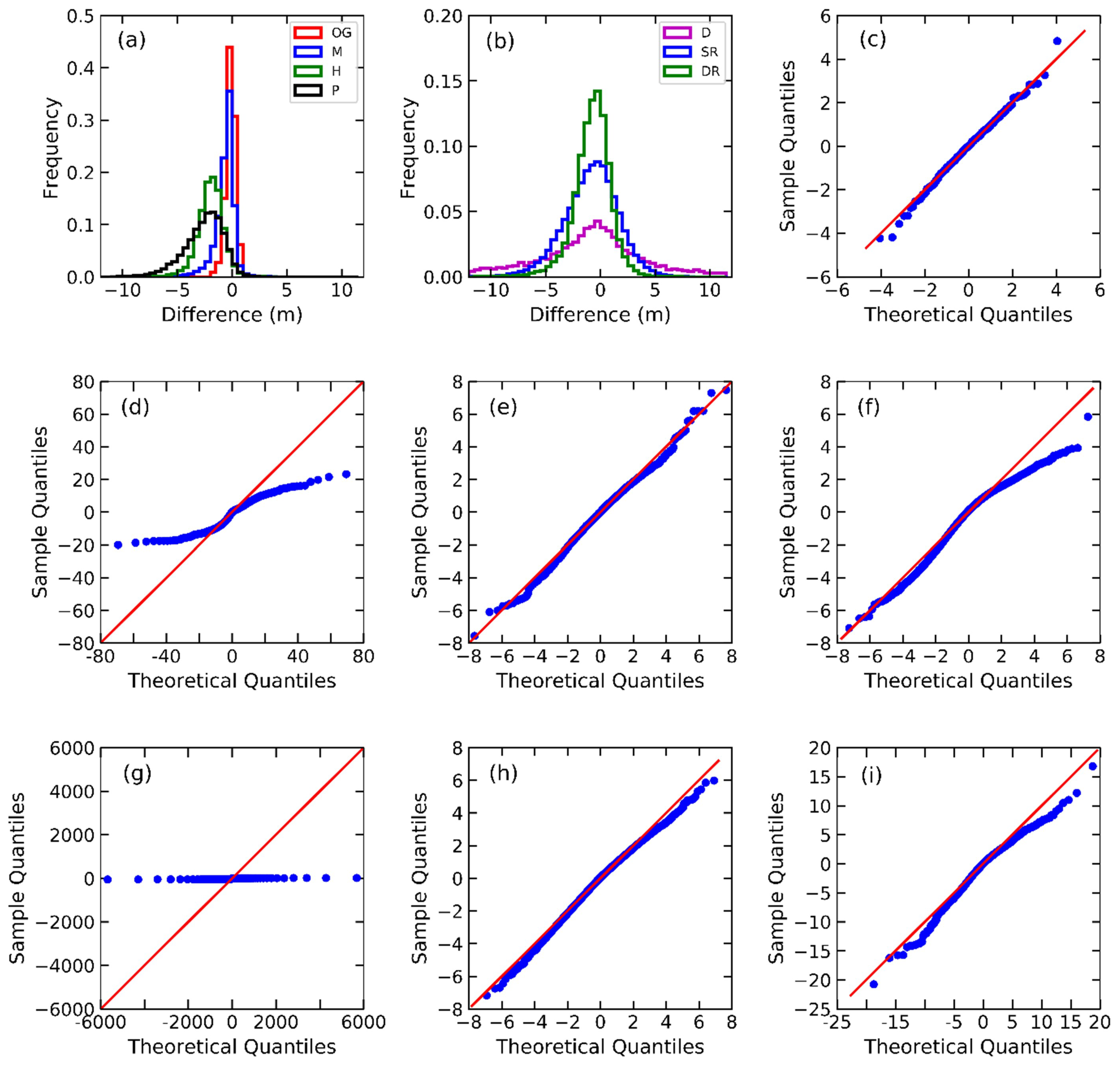
3.2. Vertical Accuracy for Different Types of Land Cover
3.2.1. Open Ground Area
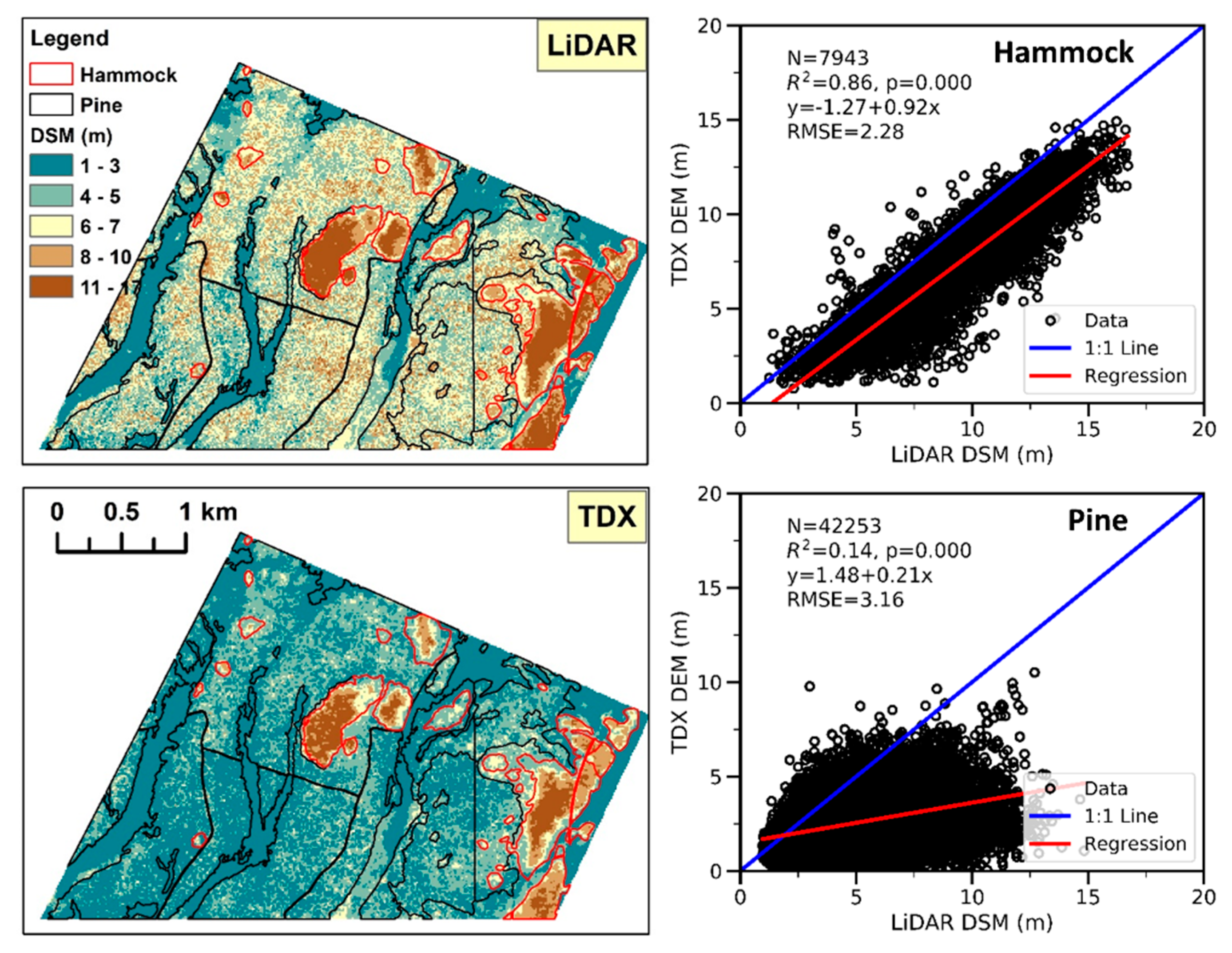
3.2.2. Forested Area
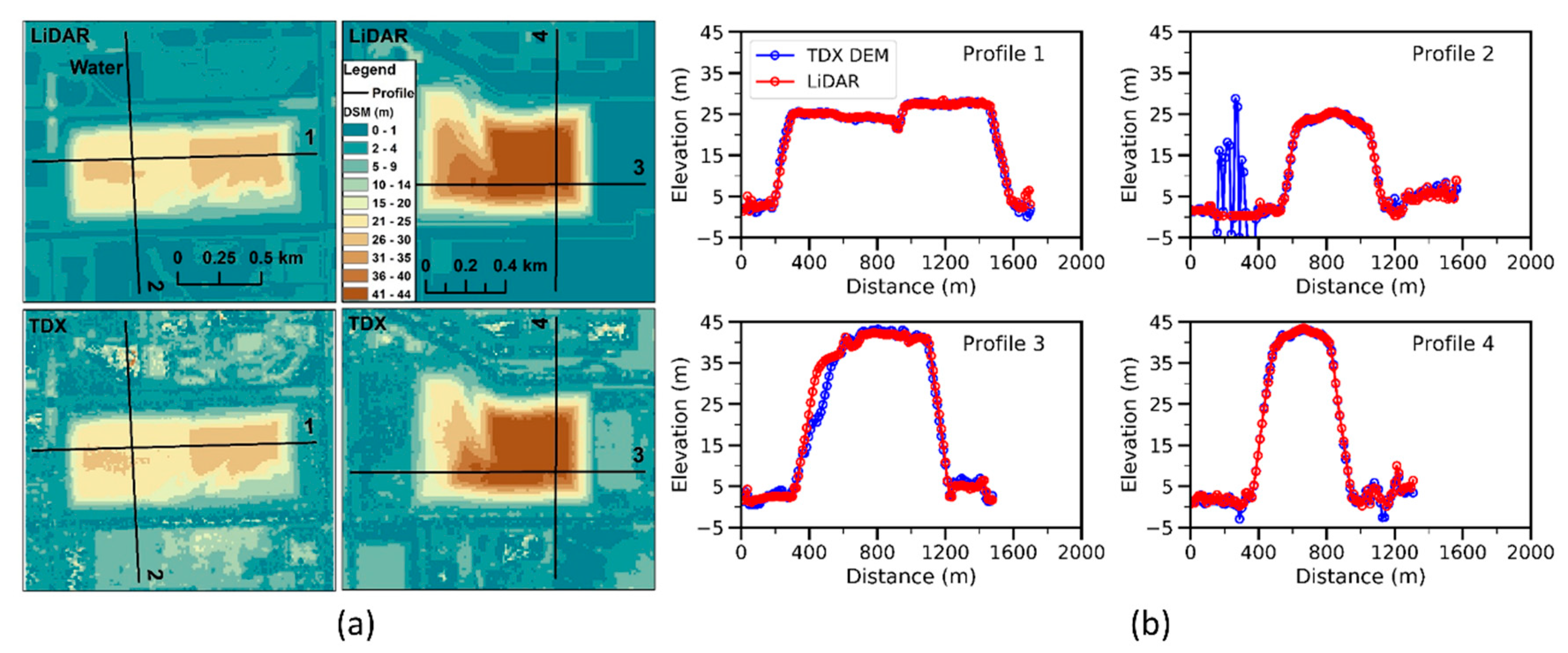
3.2.3. Built Area
3.2.4. Error Measures
4. Discussion
4.1. Open Ground
4.3. Forested Area
4.4. Built Area
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jensen, J.R. Remote Sensing of the Environment: An Earth Resource Perspective, 2nd ed.; Pearson Education: Upper Saddle River, NJ, USA, 2009. [Google Scholar]
- Jensen, J.R.; Cowen, D.C. Remote sensing of urban/suburban infrastructure and socio-economic attributes. Photogramm. Eng. Remote Sens. 1999, 65, 611–622. [Google Scholar]
- Krieger, G.; Moreira, A.; Fiedler, H.; Hajnsek, I.; Werner, M.; Younis, M.; Zink, M. TanDEM-X: A satellite formation for high-resolution SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3317–3341. [Google Scholar] [CrossRef]
- Shan, J.; Toth, C.K. Topographic Laser Ranging and Scanning: Principles and Processing; CRC Press: Boca Raton, FL, USA, 2018; ISBN 9781498772273. [Google Scholar]
- Woodhouse, I.H. Introduction to Microwave Remote Sensing; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L. The shuttle radar topography mission. Rev. Geophys. 2007, 45. [Google Scholar] [CrossRef]
- Yan, K.; Di Baldassarre, G.; Solomatine, D.P.; Schumann, G.J. A review of low-cost space-borne data for flood modelling: Topography, flood extent and water level. Hydrol. Process. 2015, 29, 3368–3387. [Google Scholar] [CrossRef]
- Li, Z.; Zhu, Q.; Gold, C. Digital Terrain Modeling: Principles and Methodology; CRC Press: Boca Raton, FL, USA, 2005; ISBN 9780415324625. [Google Scholar]
- Rodriguez, E.; Morris, C.S.; Belz, J.E. A global assessment of the SRTM performance. Photogramm. Eng. Remote Sens. 2006, 72, 249–260. [Google Scholar] [CrossRef]
- Falorni, G.; Teles, V.; Vivoni, E.R.; Bras, R.L.; Amaratunga, K.S. Analysis and characterization of the vertical accuracy of digital elevation models from the Shuttle Radar Topography Mission. J. Geophys. Res. Earth Surf. 2005, 110, F02005. [Google Scholar] [CrossRef]
- Sanders, B.F. Evaluation of on-line DEMs for flood inundation modeling. Adv. Water Resour. 2007, 30, 1831–1843. [Google Scholar] [CrossRef]
- Rizzoli, P.; Martone, M.; Gonzalez, C.; Wecklich, C.; Tridon, D.B.; Bräutigam, B.; Bachmann, M.; Schulze, D.; Fritz, T.; Huber, M. Generation and performance assessment of the global TanDEM-X digital elevation model. ISPRS J. Photogramm. Remote Sens. 2017, 132, 119–139. [Google Scholar] [CrossRef]
- Wessel, B. TanDEM-X Ground Segment–DEM Products Specification Document; German Space Center: Cologne, Germany, 2016. [Google Scholar]
- Zink, M.; Bachmann, M.; Brautigam, B.; Fritz, T.; Hajnsek, I.; Moreira, A.; Wessel, B.; Krieger, G. TanDEM-X: The new global DEM takes shape. IEEE Geosci. Remote Sens. Mag. 2014, 2, 8–23. [Google Scholar] [CrossRef]
- Huber, M.; Wessel, B.; Kosmann, D.; Felbier, A.; Schwieger, V.; Habermeyer, M.; Wendleder, A.; Roth, A. Ensuring globally the TanDEM-X height accuracy: Analysis of the reference data sets ICESat, SRTM and KGPS-Tracks. In Proceedings of the 2009 IEEE International Conference on Geoscience and Remote Sensing, Cape Town, South Africa, 12–17 July 2009; Volume 2, pp. 769–772. [Google Scholar]
- Wessel, B.; Gruber, A.; Huber, M.; Breunig, M.; Wagenbrenner, S.; Wendleder, A.; Roth, A. Validation of the absolute height accuracy of TanDEM-X DEM for moderate terrain. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 3394–3397. [Google Scholar]
- Wessel, B.; Huber, M.; Wohlfart, C.; Marschalk, U.; Kosmann, D.; Roth, A. Accuracy assessment of the global TanDEM-X digital elevation model with GPS data. ISPRS J. Photogramm. Remote Sens. 2018, 139, 171–182. [Google Scholar] [CrossRef]
- Soergel, U.; Jacobsen, K.; Schack, L. The TanDEM-X Mission: Data collection and deliverables. In Photogrammetric Week; Institute for Photogrammetry: Stuttgart, Germany, 2013; pp. 193–203. Available online: http://www.ifp.uni-stuttgart.de/publications/phowo13/170Soergel.pdf (accessed on 27 January 2019).
- Hajnsek, I.; Busche, T.; Krieger, G.; Zink, M.; Schulze, D.; Moreira, A. TanDEM-X Ground Segment Announcement of Opportunity: TanDEM-X Science Phase; TD-PD-PL-0032; German Aerospace Center, Microwaves and Radar Institute: Weßling, Germany, 2014. [Google Scholar]
- Baade, J.; Schmullius, C. TanDEM-X IDEM precision and accuracy assessment based on a large assembly of differential GNSS measurements in Kruger National Park, South Africa. ISPRS J. Photogramm. Remote Sens. 2016, 119, 496–508. [Google Scholar] [CrossRef]
- Balzter, H.; Baade, J.; Rogers, K. Validation of the TanDEM-X Intermediate digital elevation model with airborne LiDAR and differential GNSS in Kruger National Park. IEEE Geosci. Remote Sens. Lett. 2016, 13, 277–281. [Google Scholar] [CrossRef]
- Feng, L.; Muller, J.P. ICESat validation of TanDEM-X I-DEMS over the UK. ISPRS-International Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XLI-B4, 129–136. [Google Scholar] [CrossRef]
- Schlund, M.; von Poncet, F.; Kuntz, S.; Boehm, H.-D.V.; Hoekman, D.H.; Schmullius, C. TanDEM-X elevation model data for canopy height and aboveground biomass retrieval in a tropical peat swamp forest. Int. J. Remote Sens. 2016, 37, 5021–5044. [Google Scholar] [CrossRef]
- Sadeghi, Y.; St-Onge, B.; Leblon, B.; Simard, M. Canopy height model (CHM) derived from a TanDEM-X InSAR DSM and an airborne lidar DTM in boreal forest. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 381–397. [Google Scholar] [CrossRef]
- Schreyer, J.; Lakes, T. Deriving and evaluating city-wide vegetation heights from a TanDEM-X DEM. Remote Sens. 2016, 8, 940. [Google Scholar] [CrossRef]
- Marconcini, M.; Marmanis, D.; Esch, T.; Felbier, A. A novel method for building height estmation using TanDEM-X data. In Proceedings of the 2014 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Quebec City, QC, Canada, 13–18 July 2014; pp. 4804–4807. [Google Scholar]
- Hajnsek, I.; Busche, T.; Schulze, D.; Buckreub, S.; Moreira, A. TanDEM-X: TanDEM-X Digital Elevation Models Announcement of Opportunity; TD-PD-AO-0033; German Aerospace Center, Microwaves and Radar Institute: Weßling, Germany, 2016. [Google Scholar]
- Renken, R.A.; Dixon, J.; Koehmstedt, J.; Ishman, S.; Lietz, A.C.; Marella, R.L.; Telis, P.; Rodgers, J.; Memberg, S. Impact of Anthropogenic Development on Coastal Ground-Water Hydrology in Southeastern Florida, 1900–2000; USGS: Reston, VA, USA, 2005; Volume 1.
- Zhang, K. Analysis of non-linear inundation from sea-level rise using LIDAR data: A case study for South Florida. Clim. Chang. 2011, 106, 537–565. [Google Scholar] [CrossRef]
- Gruber, A.; Wessel, B.; Huber, M.; Roth, A. Operational TanDEM-X DEM calibration and first validation results. ISPRS J. Photogramm. Remote Sens. 2012, 73, 924–2716. [Google Scholar] [CrossRef]
- Gruber, A.; Wessel, B.; Martone, M.; Roth, A. The TanDEM-X DEM mosaicking: Fusion of multiple acquisitions using InSAR quality parameters. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 1047–1057. [Google Scholar] [CrossRef]
- America, A.C. Surveyor and Mapper Report for the 2015 Aerial LiDAR Specific Purpose Survey of Miami-Dade County; Aerial Cartographics of America: Orlando, FL, USA, 2015. Available online: https://coast.noaa.gov/htdata/lidar2_z/geoid12b/data/5038/supplemental/fl2015_miami_dade_m5038_lidar_report.pdf (accessed on 27 January 2019).
- SFWMD. 2009 SFWMD Photointeperation Key; SFWMD: West Palm Beach, FL, USA, 2011.
- Welch, R.; Madden, M.; Doren, R.F. Mapping the Everglades. Photogramm. Eng. Remote Sens. 1999, 65, 163–170. [Google Scholar]
- Hochmair, H.H.; Gann, D.; Benjamin, A.; Fu, Z. Miami-Dade County Urban Tree Canopy Assessment; GIS Center, Florida International University: Miami, FL, USA, 2016. [Google Scholar]
- FDOT. Florida Land Use and Cover and Forms Classification System: Handbook, 3rd ed.; Thematic Mapping Section: Tallahassee, FL, USA, 1999.
- Wendleder, A.; Wessel, B.; Roth, A.; Breunig, M.; Martin, K.; Wagenbrenner, S. TanDEM-X Water Indication Mask: Generation and First Evaluation Results. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 171–179. [Google Scholar] [CrossRef] [Green Version]
- Davis, J. Statistics and Data Analysis In Geology, 3rd ed.; John Willey & Sons, Inc.: New York, NY, USA, 2002; ISBN 978-0-471-17275-8. [Google Scholar]
- Höhle, J.; Höhle, M. Accuracy assessment of digital elevation models by means of robust statistical methods. ISPRS J. Photogramm. Remote Sens. 2009, 64, 398–406. [Google Scholar] [CrossRef] [Green Version]
- Müller, J.; Gärtner-Roer, I.; Thee, P.; Ginzler, C. Accuracy assessment of airborne photogrammetrically derived high-resolution digital elevation models in a high mountain environment. ISPRS J. Photogramm. Remote Sens. 2014, 98, 58–69. [Google Scholar] [CrossRef]
- Hampel, F.R. The influence curve and its role in robust estimation. J. Am. Stat. Assoc. 1974, 69, 383–393. [Google Scholar] [CrossRef]
- Leys, C.; Ley, C.; Klein, O.; Bernard, P.; Licata, L. Detecting outliers: Do not use standard deviation around the mean, use absolute deviation around the median. J. Exp. Soc. Psychol. 2013, 49, 764–766. [Google Scholar] [CrossRef] [Green Version]
- Ross, M.S.; O’Brien, J.J.; Ford, R.G.; Zhang, K.; Morkill, A. Disturbance and the rising tide: The challenge of biodiversity management on low-island ecosystems. Front. Ecol. Environ. 2009, 7, 471–478. [Google Scholar] [CrossRef]
- Geiß, C.; Wurm, M.; Breunig, M.; Felbier, A.; Taubenböck, H. Normalization of TanDEM-X DSM data in urban environments with morphological filters. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4348–4362. [Google Scholar] [CrossRef]
- Gutenson, J.L.; Follum, M.L.; Snow, A.D.; Wahl, M.D. Large-scale flood inundation modeling in data sparse environments using TanDEM-X terrain data. Open Water J. 2017, 4, 4. [Google Scholar]
- Rossi, C.; Gernhardt, S. Urban DEM generation, analysis and enhancements using TanDEM-X. ISPRS J. Photogramm. Remote Sens. 2013, 85, 120–131. [Google Scholar] [CrossRef]
- Schreyer, J.; Geiß, C.; Lakes, T. TanDEM-X for large-Area modeling of urban vegetation height: Evidence from Berlin, Germany. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 1876–1887. [Google Scholar] [CrossRef]
- Lagomasino, D.; Fatoyinbo, T.; Lee, S.; Feliciano, E.; Trettin, C.; Simard, M. A comparison of mangrove canopy height using multiple independent measurements from land, air, and space. Remote Sens. 2016, 8, 327. [Google Scholar] [CrossRef]
- Sadeghi, Y.; St-Onge, B.; Leblon, B.; Prieur, J.-F.; Simard, M. Mapping boreal forest biomass from a SRTM and TanDEM-X based on canopy height model and Landsat spectral indices. Int. J. Appl. Earth Obs. Geoinf. 2018, 68, 202–213. [Google Scholar] [CrossRef]
- Feliciano, E.A.; Wdowinski, S.; Potts, M.D.; Lee, S.-K.; Fatoyinbo, T.E. Estimating Mangrove Canopy Height and Above-Ground Biomass in the Everglades National Park with Airborne LiDAR and TanDEM-X Data. Remote Sens. 2017, 9, 702. [Google Scholar] [CrossRef]
- Zhang, K.; Thapa, B.; Ross, M.; Gann, D. Remote sensing of seasonal changes and disturbances in mangrove forest: A case study from South Florida. Ecosphere 2016, 7, 1–23. [Google Scholar] [CrossRef]
- Simard, M.; Zhang, K.; Rivera-Monroy, V.H.; Ross, M.S.; Ruiz, P.L.; Castañeda-Moya, E.; Twilley, R.R.; Rodriguez, E. Mapping height and biomass of mangrove forests in Everglades National Park with SRTM elevation data. Photogramm. Eng. Remote Sens. 2006, 72, 299–311. [Google Scholar] [CrossRef]
- Houle, P.; Zhang, K.; Ross, M.; Simard, M. Use of airborne lidar for the assessment of landscape structure in the pine forests of Everglades national park. In Proceedings of the 2006 IEEE International Conference on Geoscience and Remote Sensing, Denver, CO, USA, 31 July–4 August 2006; pp. 1960–1963. [Google Scholar]





| LC | NP/PC | ME | MD | AME | MNB | SD | RMSE | NMAD | LE90 | R2 | PV |
|---|---|---|---|---|---|---|---|---|---|---|---|
| EA-1 | 24671844/0 | −0.51 | 0.42 | 0.94 | 2.8 | 2.19 | 2.25 | 0.62 | 2.30 | 0.52 | 0.000 |
| EA-2 | 24284337/1.6 | −0.50 | 0.41 | 0.89 | 2.9 | 1.73 | 1.80 | 0.61 | 2.23 | 0.65 | 0.000 |
| EA-3 | 24362012/1.3 | −0.49 | 0.41 | 0.90 | 2.8 | 1.74 | 1.81 | 0.61 | 2.26 | 0.64 | 0.000 |
| EA-4 | 24057905/2.5 | −0.49 | 0.40 | 0.88 | 2.9 | 1.60 | 1.67 | 0.60 | 2.21 | 0.68 | 0.000 |
| OG-1 | 326/0 | −0.15 | −0.13 | 0.37 | −7.3 | 0.47 | 0.49 | 0.41 | 0.79 | 0.99 | 0.000 |
| OG-2 | 319/2.1 | −0.14 | −0.13 | 0.36 | −6.5 | 0.46 | 0.48 | 0.41 | 0.78 | 0.99 | 0.000 |
| OG-3 | 325/0.3 | −0.15 | −0.13 | 0.37 | −7.3 | 0.47 | 0.49 | 0.41 | 0.80 | 0.99 | 0.000 |
| OG-4 | 319/2.1 | −0.14 | −0.13 | 0.36 | −6.5 | 0.46 | 0.48 | 0.41 | 0.78 | 0.99 | 0.000 |
| M-1 | 94040/0 | −0.65 | −0.46 | 0.77 | −21.1 | 0.95 | 1.15 | 0.60 | 1.75 | 0.95 | 0.000 |
| M-2 | 93026/1.1 | −0.64 | −0.45 | 0.76 | −21.4 | 0.91 | 1.11 | 0.59 | 1.70 | 0.95 | 0.000 |
| M-3 | 93621/0.4 | −0.65 | −0.46 | 0.77 | −21.3 | 0.93 | 1.13 | 0.60 | 1.73 | 0.95 | 0.000 |
| M-4 | 92752/1.4 | −0.64 | −0.45 | 0.75 | −21.6 | 0.90 | 1.10 | 0.59 | 1.69 | 0.95 | 0.000 |
| H-1 | 7943/0 | −1.97 | −1.93 | 2.01 | −23.2 | 1.15 | 2.28 | 1.00 | 3.37 | 0.86 | 0.000 |
| H-2 | 7936/0.1 | −1.97 | −1.93 | 2.01 | −23.2 | 1.15 | 2.28 | 1.00 | 3.37 | 0.86 | 0.000 |
| H-3 | 7943/0 | −1.97 | −1.93 | 2.01 | −23.2 | 1.15 | 2.28 | 1.00 | 3.37 | 0.86 | 0.000 |
| H-4 | 7936/0.1 | −1.97 | −1.93 | 2.01 | −23.2 | 1.15 | 2.28 | 1.00 | 3.37 | 0.86 | 0.000 |
| P-1 | 42253/0 | −2.60 | −2.35 | 2.64 | −46.0 | 1.80 | 3.16 | 1.66 | 5.00 | 0.14 | 0.000 |
| P-2 | 38943/7.8 | −2.55 | −2.30 | 2.58 | −46.0 | 1.73 | 3.08 | 1.60 | 4.85 | 0.16 | 0.000 |
| P-3 | 42253/0 | −2.65 | −2.35 | 2.64 | −46.0 | 1.80 | 3.16 | 1.66 | 5.00 | 0.14 | 0.000 |
| P-4 | 38943/7.8 | −2.55 | −2.30 | 2.58 | −46.0 | 1.73 | 3.08 | 1.60 | 4.85 | 0.16 | 0.000 |
| D-1 | 12146/0 | −14.35 | −2.42 | 18.03 | −36.9 | 32.70 | 35.70 | 7.99 | 51.67 | 0.00 | 0.000 |
| D-2 | 6860/43.5 | −9.23 | −1.50 | 11.85 | −10.2 | 25.23 | 26.86 | 4.94 | 33.73 | 0.01 | 0.000 |
| D-3 | 6921/43.0 | −8.48 | −1.20 | 10.91 | −2.4 | 24.93 | 26.33 | 4.55 | 29.10 | 0.01 | 0.000 |
| D-4 | 5172/57.4 | −7.20 | −1.13 | 9.19 | −4.6 | 22.35 | 23.48 | 3.82 | 22.49 | 0.00 | 0.000 |
| SR-1 | 79565/0 | −0.86 | −0.70 | 2.01 | −1.5 | 2.48 | 2.62 | 2.31 | 4.29 | 0.44 | 0.000 |
| SR-2 | 79526/0.0 | −0.86 | −0.70 | 2.01 | −1.5 | 2.48 | 2.62 | 2.31 | 4.28 | 0.44 | 0.000 |
| SR-3 | 79523/0.1 | −0.86 | −0.70 | 2.01 | −1.5 | 2.48 | 2.62 | 2.31 | 4.29 | 0.44 | 0.000 |
| SR-4 | 79491/0.1 | −0.86 | −0.70 | 2.01 | −1.5 | 2.48 | 2.62 | 2.31 | 4.28 | 0.44 | 0.000 |
| DR-1 | 100253/0 | −0.75 | −0.62 | 1.37 | −9.1 | 1.74 | 1.89 | 1.42 | 2.90 | 0.23 | 0.000 |
| DR-2 | 99687/0.6 | −0.76 | −0.62 | 1.37 | −9.1 | 1.73 | 1.89 | 1.42 | 2.89 | 0.23 | 0.000 |
| DR-3 | 100005/0.2 | −0.75 | −0.62 | 1.37 | −9.1 | 1.73 | 1.89 | 1.42 | 2.89 | 0.23 | 0.000 |
| DR-4 | 99472/0.8 | −0.75 | −0.62 | 1.37 | −9.1 | 1.73 | 1.88 | 1.42 | 2.89 | 0.23 | 0.000 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, K.; Gann, D.; Ross, M.; Biswas, H.; Li, Y.; Rhome, J. Comparison of TanDEM-X DEM with LiDAR Data for Accuracy Assessment in a Coastal Urban Area. Remote Sens. 2019, 11, 876. https://0-doi-org.brum.beds.ac.uk/10.3390/rs11070876
Zhang K, Gann D, Ross M, Biswas H, Li Y, Rhome J. Comparison of TanDEM-X DEM with LiDAR Data for Accuracy Assessment in a Coastal Urban Area. Remote Sensing. 2019; 11(7):876. https://0-doi-org.brum.beds.ac.uk/10.3390/rs11070876
Chicago/Turabian StyleZhang, Keqi, Daniel Gann, Michael Ross, Himadri Biswas, Yuepeng Li, and Jamie Rhome. 2019. "Comparison of TanDEM-X DEM with LiDAR Data for Accuracy Assessment in a Coastal Urban Area" Remote Sensing 11, no. 7: 876. https://0-doi-org.brum.beds.ac.uk/10.3390/rs11070876