1. Introduction
Coastal regions play an important role in social and economic development around the globe [
1,
2,
3,
4,
5]. According to previous studies [
2], about 24% of the world’s population lives in coastal areas. Meanwhile, coastal regions are home to many valuable wetland ecosystems, which perform various functions beneficial to the sustainability of human society, including flooding control, water quality improvement, biodiversity conservation, maintaining the supply of fisheries and other resources, etc. [
2,
3,
4,
5]. However, due to anthropogenic activities and global climate change, coastal regions have experienced rapid land cover changes over the last few decades [
4,
5]. Therefore, accurate and timely monitoring of coastal regions by means of remote sensing is of great significance to regional, sustainable development.
In fact, accurate land cover classification of complex coastal regions is a challenging task [
2,
6,
7,
8]. The challenges are mainly two-fold. On the one hand, the highly fragmented landscape of coastal regions leads to large variations in the shape and scale of land objects, which increases the interclass variability and decreases the intraclass similarity. On the other hand, some vegetation classes (e.g., grassland and cropland) may have overlapping spectral reflectance at peak biomass, which also raises difficulties in accurate classification.
Many studies have been conducted on accurate coastal land cover classification [
2,
6,
7,
8]. In coastal areas, although some crops and natural vegetation share similar spectral features during peak growing season, they may have different seasonal variations and temporal characteristics. Therefore, the inclusion of multitemporal remote sensing data could improve classification accuracy when compared with monotemporal data alone. Davranche et al. [
6] used multiseasonal SPOT-5 imagery and decision trees for coastal wetland classification in southern France. Yang et al. [
7] adopted seasonal optical imagery for coastal land cover classification and demonstrated that combining multiseasonal images considerably improves classification accuracy over any single-date classification. In our previous work [
8], we also utilized multitemporal Landsat data to monitor cropland dynamics of the Yellow River Delta and justified the role of multitemporal data in classification.
Meanwhile, because of the availability of diverse remote sensors, researchers have started to integrate multisensor data for better classification of coastal areas [
9,
10,
11,
12,
13]. Specifically, fusion of optical and radar data has been widely studied [
9,
10,
11,
12,
13]. Optical images mainly contain information regarding reflectance and emissivity characteristics of land surfaces [
9], while radar data are associated with the structural, textural, and dielectric properties of land objects [
10]. Therefore, integration of optical and radar data can complement each other, resulting in an improved coastal land cover classification. Rodrigues et al. [
9] used multisensor data from Landsat-7 and RADARSAT-1 to identify and map tropical coastal wetlands in the Amazon of northern Brazil. Beijma et al. [
10] investigated the uses of multisource airborne radar and optical data to map natural coastal salt marsh vegetation habitats.
Since the successful implementation of the European Copernicus program created by the European Space Agency (ESA), Sentinel-1 radar data and Sentinel-2 optical data are now available via open access, providing new insights for remote sensing applications, especially for large-scale environmental monitoring [
14,
15,
16,
17,
18,
19]. For instance, Hird et al. developed a workflow for large-area probabilistic wetland mapping based on Google Earth Engine (GEE) and Sentinel-1 and 2 data [
14]. Mahdianpari et al. also adopted GEE and multisource Sentinel data to generate the first detailed (category-based) provincial-level wetland inventory map [
15]. Therefore, we are highly interested in integrating multitemporal and multisensor Sentinel data for accurate coastal land cover classification.
In addition, all the above studies are based on handcrafted features and conventional machine-learning classifiers, which may fail in obtaining high-level features of complex heterogeneous coastal landscapes. Deep learning [
20], on the other hand, has the ability to discover informative features with multiple levels of representation and has achieved an astonishing performance in computer vison applications [
21,
22,
23,
24,
25,
26], such as image classification [
21], object detection [
23], and semantic segmentation [
24]. Recently, deep learning, especially deep convolutional neural networks (CNNs), has also been successfully applied in many remote sensing applications [
27,
28,
29,
30,
31,
32,
33,
34,
35,
36,
37]. Rezaee et al. [
34] applied a pre-trained AlexNet [
21] for wetland mapping using monotemporal optical imagery. Rußwurm et al. [
35] utilized sequential recurrent encoders and multitemporal Sentinel-2 optical data for land cover classification, which achieved state-of-the-art classification accuracies. Ji et al. [
36] proposed a three-dimensional (3D) CNN for crop classification with multitemporal remote sensing images and concluded that a 3D CNN was suitable in characterizing dynamics of crop growth. Mahdianpari et al [
38]. investigated state-of-the-art deep learning models for classification of complex wetland classes and indicated that InceptionResNetV2, ResNet50, and Xception were distinguished as the top three models.
Despite improvements made by deep learning in the remote sensing field, two challenges of coastal land cover classification mentioned above still remain and need to be solved. In the context of deep learning, the two issues can be revisited as follows: (1) how to build a concise and effective deep learning model that accounts for variations in shapes and scales in fragmented coastal regions, and (2) how to design a fusion mechanism that adaptively fuses multitemporal and multisensor remote sensing data.
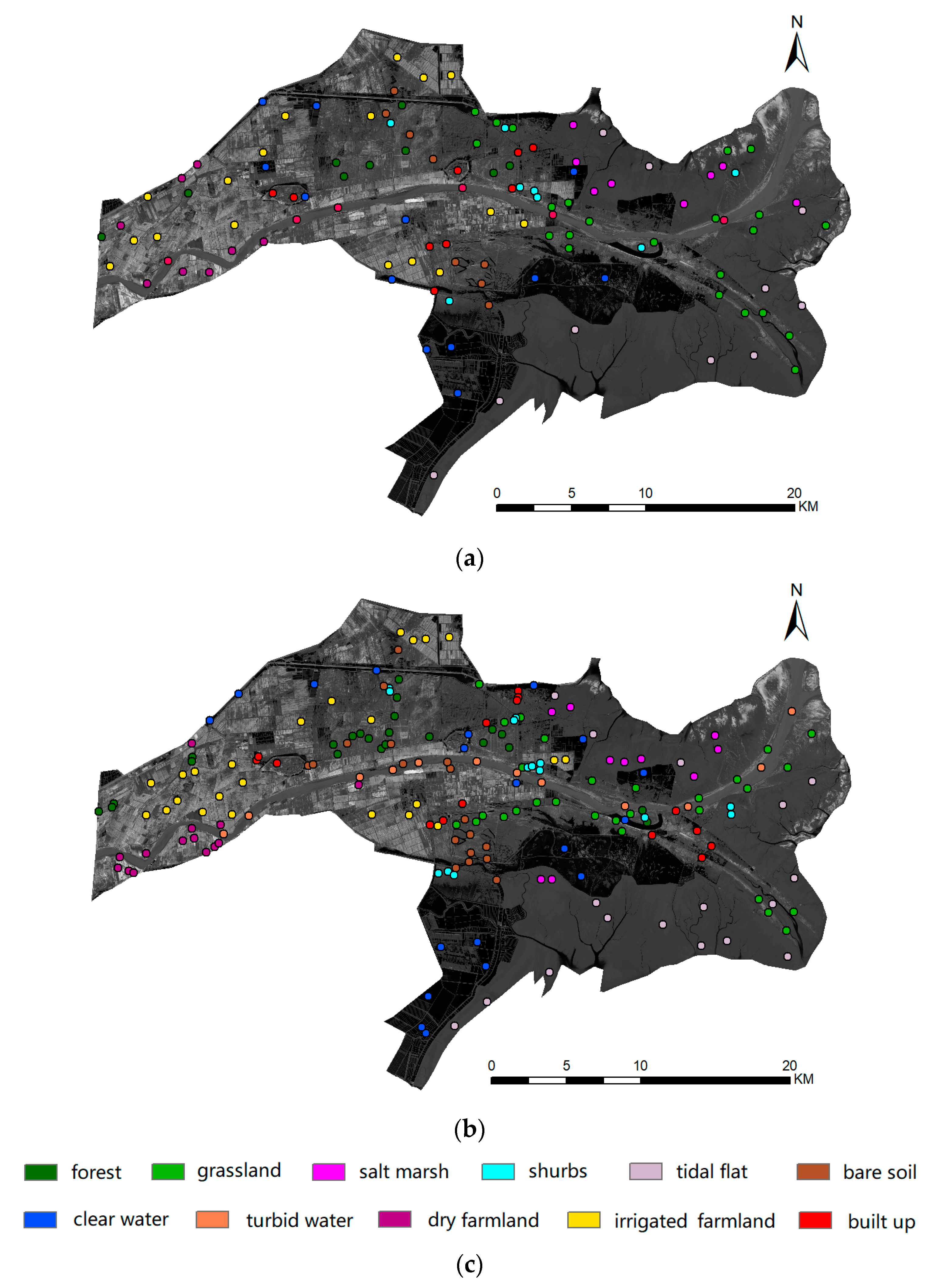
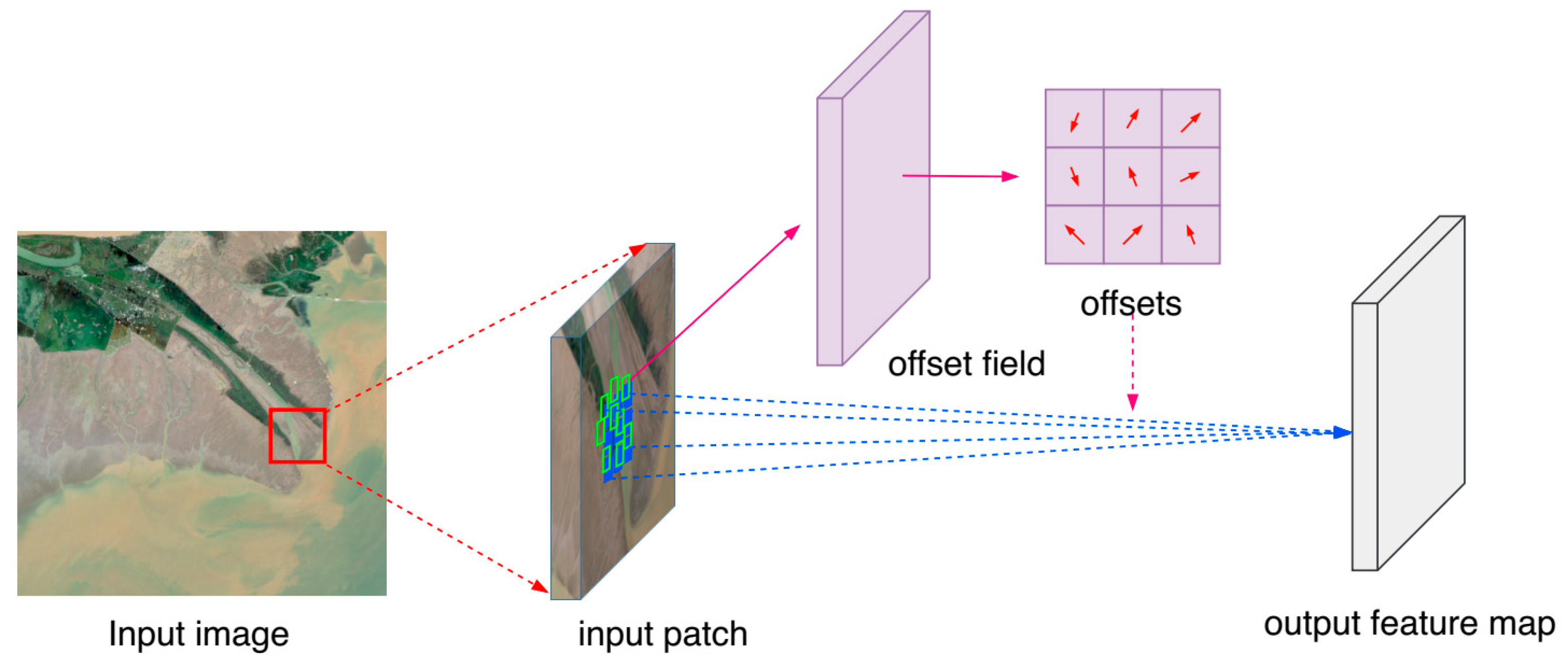
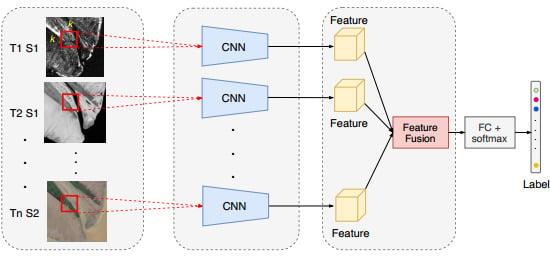
To address these issues, this study proposes a multibranch convolutional neural network (MBCNN) for coastal land cover classification using multitemporal and multisensor Sentinel data. First, a single-branch CNN is proposed to extract representative features from each monotemporal and single-sensor Sentinel datum. A deformable multiscale residual block is utilized in the single-branch CNN to account for shape and scale variations. Afterwards, multiple single-branch CNNs are integrated through an adaptive fusion module, which are inspired by squeeze-and-excitation networks [
25], to predict the final land cover category. The selected study region is the Yellow River Delta, which is the largest natural delta of China and home to abundant coastal wetlands [
39,
40,
41,
42].
The rest of the paper is organized as follows.
Section 2 introduces the study area and the dataset used.
Section 3 presents the architecture and training details of the proposed multibranch neural network.
Section 4 shows the experimental results and discussion, while
Section 5 provides the main conclusions and suggestions for future work.
The contributions of this study are mainly two-fold. (1) We have designed a concise yet effective deep learning model for coastal land cover classification, which adopts deformable convolutional layers to account for variations of scales and shapes of coastal landscapes. (2) We have proposed a feature-level fusion module based on squeeze-and-excitation networks for multitemporal and multisensor Sentinel data fusion to boost coastal land cover classification accuracy.
5. Conclusions
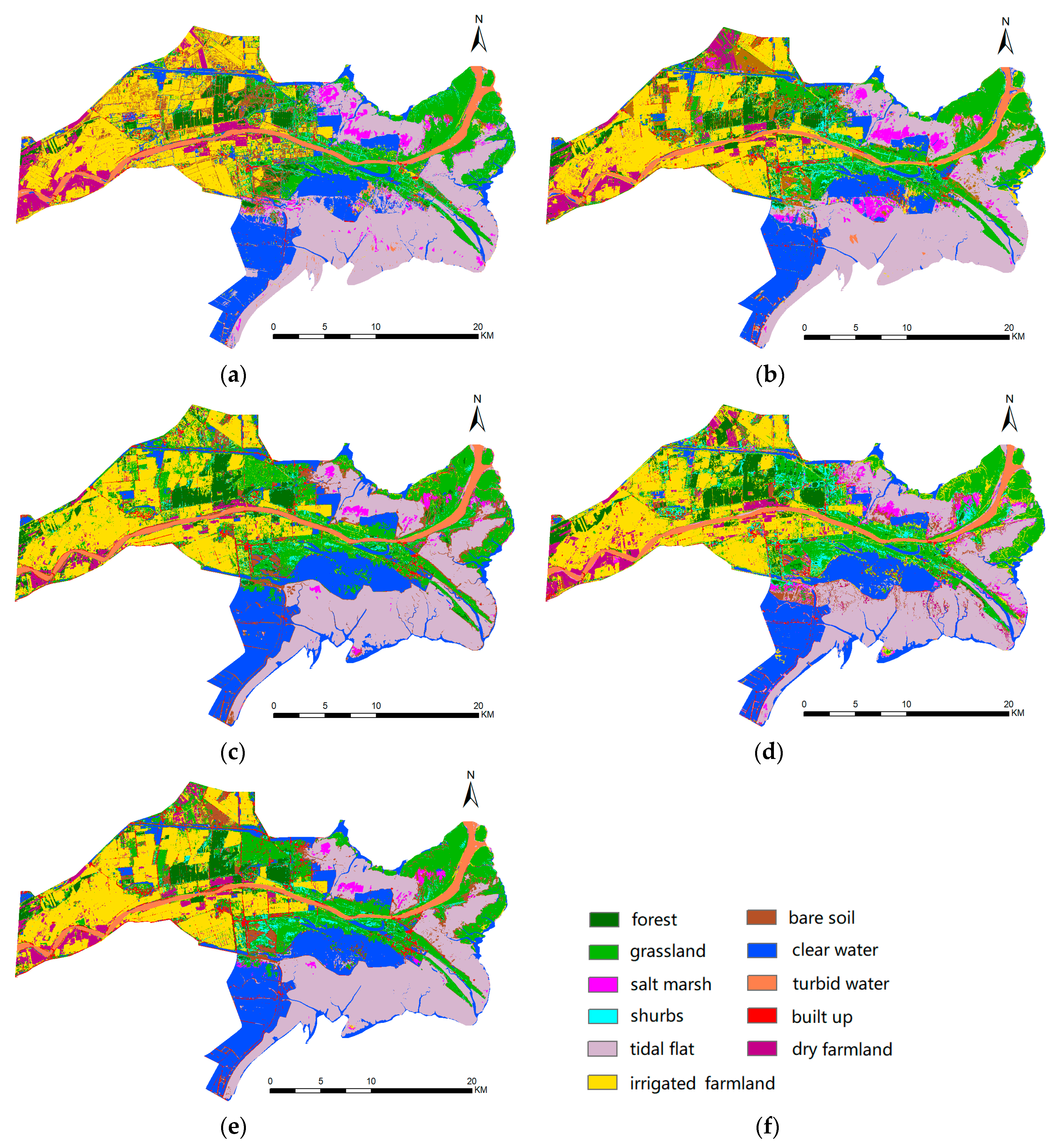
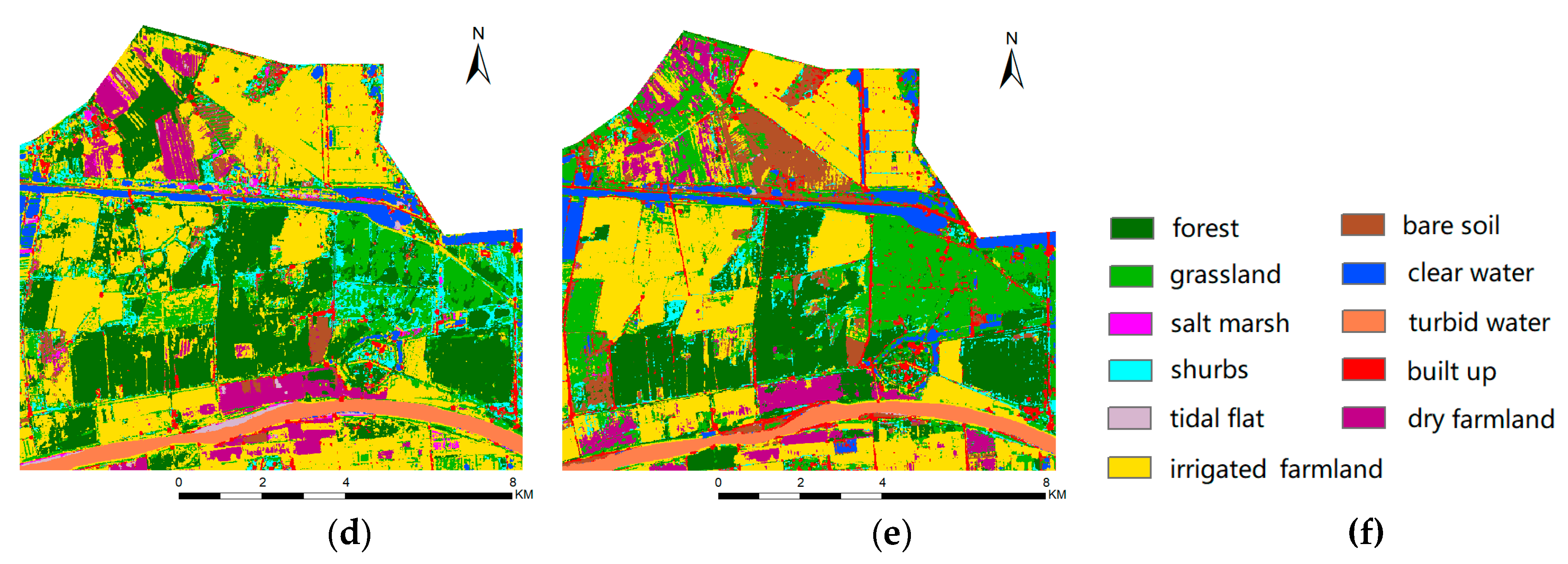
This paper proposed a multibranch convolutional neural network for fusion of multitemporal and multisensor Sentinel data for coastal land cover classification. The proposed neural network leverages a series of single-branch CNNs for feature extraction from single-date and single-sensor Sentinel data. Deformable convolutions and multiscale residual blocks were introduced to account for the variations in shapes and scales of coastal land objects. Features extracted from each branch were then aggregated using an adaptive fusion module to make the final land cover predictions.
The experiments were performed in the Yellow River Delta, which is the largest natural delta in China. The results indicated that the proposed multibranch CNN achieved good performance with an overall accuracy of 93.78% and a Kappa coefficient of 0.9297. The introduction of deformable convolutions increased the OA by 2.09%, which justified its role in modeling complex and fragmented coastal landscapes. Meanwhile, inclusion of multitemporal data improved the OA by 1.15%–11.85%, with an average increase of 6.85%, which justified the importance of temporal information in coastal land cover classification. Moreover, when compared with optical data alone, the inclusion of radar data increased the OA from 90.54% to 93.78% with an improvement of 3.24%, which indicated that the fusion of multisensor Sentinel data could enhance the separability of coastal land cover types. However, using radar data alone cannot achieve an accurate classification result. The proposed adaptive fusion method improved the OA by an increase of 2.28% when compared with the feature-stacking method, which also justified its effectiveness in multisource data fusion.
This paper demonstrates that the proposed multibranch CNN can effectively extract and integrate features from multitemporal and multisensor Sentinel-1 and Sentinel-2 remote sensing data, which achieves good performance in coastal land cover classification. In addition, the proposed network architecture can be considered as a general framework for multitemporal and multisensor data fusion. Future work should consider more study cases to further verify the effectiveness of the proposed MBCNN.